2021-2022学年苏科版八年级数学上册期中复习测评 第3章勾股定理 (word版含解析)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册期中复习测评 第3章勾股定理 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 19:39:25 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学上册《第3章勾股定理》期中复习综合测评(附答案)
一.选择题(共8小题,满分32分)
1.在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=5:3:2,③∠A=90°﹣∠B,④∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,AB=10,AC=13,AD⊥BC,垂足为D,M为AD上任一点,则MC2﹣MB2等于( )
A.23 B.46 C.65 D.69
3.已知:△ABC中,∠C=45°,D为BC边上一点,AD=AB,BD=2,BH⊥AD于H,BH延长线交AC于E,则CE的长为( )
A. B. C. D.1
4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如图,设直角三角形较长直角边长为a,较短直角边长为b.若大正方形面积是9,小正方形面积是1,则ab的值是( )
A.4 B.6 C.8 D.10
5.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两个直角边和为( )
A.5 B.7 C.25 D.3
6.若一个三角形的三个外角之比为3:4:5,则该三角形为( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
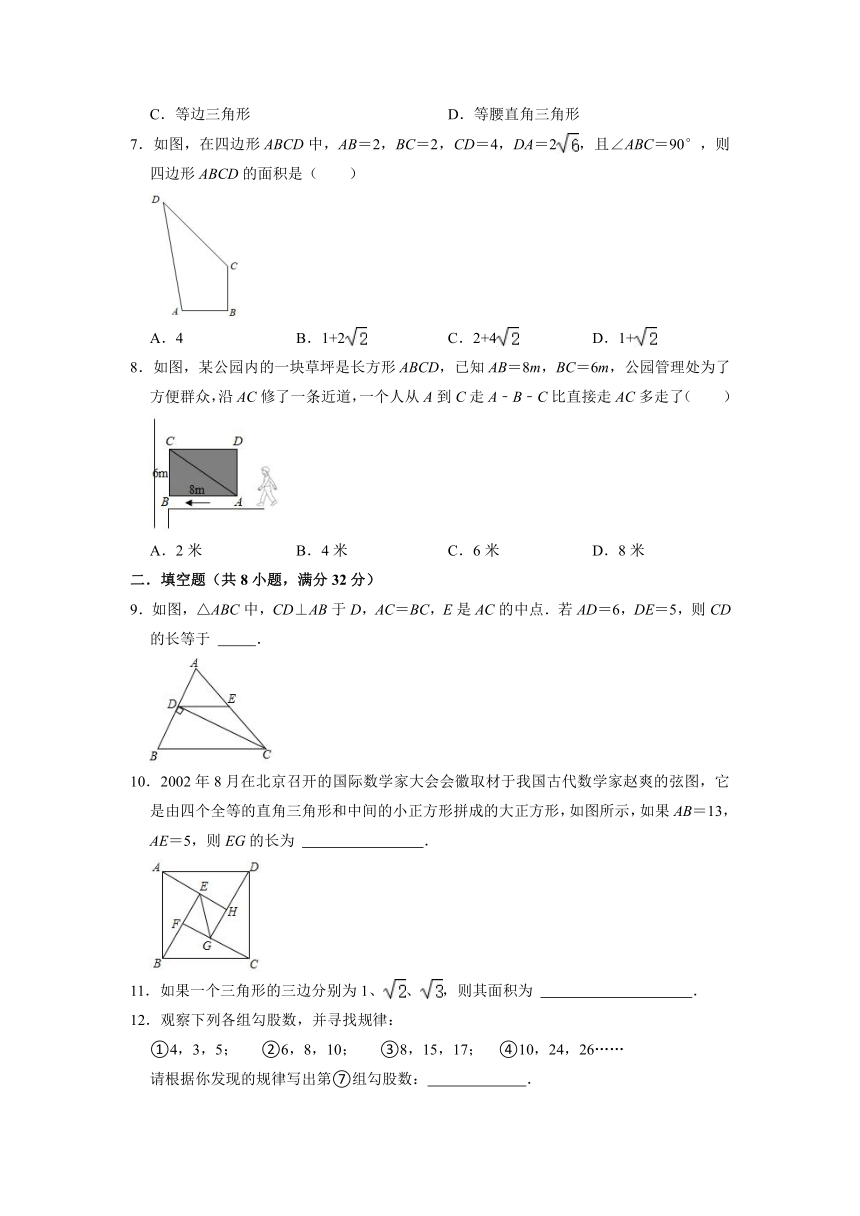
7.如图,在四边形ABCD中,AB=2,BC=2,CD=4,DA=2,且∠ABC=90°,则四边形ABCD的面积是( )
A.4 B.1+2 C.2+4 D.1+
8.如图,某公园内的一块草坪是长方形ABCD,已知AB=8m,BC=6m,公园管理处为了方便群众,沿AC修了一条近道,一个人从A到C走A﹣B﹣C比直接走AC多走了( )
A.2米 B.4米 C.6米 D.8米
二.填空题(共8小题,满分32分)
9.如图,△ABC中,CD⊥AB于D,AC=BC,E是AC的中点.若AD=6,DE=5,则CD的长等于 .
10.2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果AB=13,AE=5,则EG的长为 .
11.如果一个三角形的三边分别为1、、,则其面积为 .
12.观察下列各组勾股数,并寻找规律:
①4,3,5; ②6,8,10; ③8,15,17; ④10,24,26……
请根据你发现的规律写出第⑦组勾股数: .
13.我们学习了勾股定理的逆定理后,知道了勾股数的概念.观察下列勾股数:4、3、5;6、8、10;8、15、17;10、24、26;…,发现这些勾股数的第一个数都是偶数,且从4起再没有间断过.观察并利用上述勾股数的规律,若第一个数用字母n表示(n为偶数,且n≥4),则最大的数可以用含n的式子表示为 .
14.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB、AC长分别为13米、20米,主梁AD的高度为12米,则固定点B、C之间的距离为 米.
15.《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC= 尺.
16.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 .
三.解答题(共8小题,满分56分)
17.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
18.如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD=
(1)求AD的长;
(2)求证:△ABC是直角三角形.
19.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C所对的边.
(1)若a=5,b=4,求c的长;
(2)若三条边中有两条边的长分别为5和4,求第三条边的长.
20.如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.
(1)求证:∠ADC=90°;
(2)求图中阴影部分土地的面积.
21.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度AB.
22.如图,在△ABC中,AB=4,BC=8,AC的垂直平分线交AC于点D,交BC于点E,CE=3,连接AE.
(1)求证:△ABE是直角三角形;
(2)求△ACE的面积.
23.法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的关系式,显然,满足这个关系式的x,y,z有无数组.当x,y,z都为正整数时,我们把这样的三个数x,y,z叫做勾股数.如,3,4,5就是一组勾股数.
(1)请你再写出两组勾股数: , ;
(2)古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2﹣1,z=n2+1,那么,x,y,z为勾股数,请你加以证明.
24.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
参考答案
一.选择题(共8小题,满分32分)
1.解:①∵∠A+∠B=∠C,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形;
②∵∠A:∠B:∠C=5:3:2,
设∠A=5x,则∠B=3x,∠C=2x,
∴5x+2x+3x=180,
解得:x=18°,
∴∠5=18°×5=90°,
∴△ABC是直角三角形;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
∴△ABC是直角三角形;
④∵3∠C=2∠B=∠A,
∴∠A+∠B+∠C=∠A+∠A+∠A=180°,
∴∠A=()°,
∴△ABC为钝角三角形.
∴能确定△ABC是直角三角形的有①②③共3个,
故选:C.
2.解:在Rt△ABD和Rt△ADC中,
BD2=AB2﹣AD2,CD2=AC2﹣AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2﹣AD2+MD2,MC2=CD2+MD2=AC2﹣AD2+MD2,
∴MC2﹣MB2
=(AC2﹣AD2+MD2)﹣(AB2﹣AD2+MD2)
=AC2﹣AB2
=132﹣102
=69.
故选:D.
3.解:过点A作AM⊥BD于点M,过点E作EF⊥BC于点F,
∵AB=AD,AM⊥BC,
∴∠BAM=∠DAM,BM=DM,
∵BH⊥AD,
∴∠HBD+∠HDB=90°,
又∵∠HDB+∠MAD=90°,
∴∠HBD=∠MAD,
∴∠HBD=∠BAM=∠MAD,
∵∠C=45°,
∴∠MAC=∠FEC=45°,
∵∠AEB=∠C+∠EBC=45°+∠EBC,∠BAC=∠MAC+∠BAM=45°+∠BAM,
∴∠AEB=∠BAC,
∴AB=BE,
在△ABM和△BEF中,
,
∴△ABM≌△BEF(AAS),
∴EF=BM=1,
∴CE=EF=,
故选:A.
4.解:∵直角三角形较长直角边长为a,较短直角边长为b,大正方形面积是9,
∴a2+b2=9,
∵小正方形面积是1,
∴(a﹣b)2=1,
∴a2+b2﹣2ab=1,
∴9﹣2ab=1,
∴ab=4,
故选:A.
5.解:设直角三角形的两直角边为a、b,
由题意可得,ab×4=13﹣1,a2+b2=13,
∴ab=6,
∴(a+b)2=a2+2ab+b2=(a2+b2)+2ab=13+2×6=13+12=25,
∴a+b=5或a+b=﹣5(舍去),
故选:A.
6.解:设三角形的三个外角的度数分别为3x、4x、5x,
则3x+4x+5x=360°,
解得,x=30°,
∴三角形的三个外角的度数分别为90°、120°、150°,
对应的三个内角的度数分别为90°、60°、30°,
∴此三角形为直角三角形,
故选:A.
7.解:连接AC,
∵∠ABC=90°,AB=BC=2,
在直角三角形ABC中,AC2=AB2+BC2,
∴AC2=8,
又∵DC=4,AD=2,
∴DC2=16,AD2=24,
在三角形ACD中有:DC2+AC2=16+8=24=AD2,
∴三角形ACD是直角三角形,∠DCA=90°,
∴四边形ABCD的面积=三角形DCA的面积+三角形ABC的面积=DC×AC+AB×BC=×4×2+×2×2=4+2,
故选:C.
8.解:由勾股定理,得
捷径AC==10(m),
多走了8+6﹣10=4(m).
故选:B.
二.填空题(共8小题,满分32分)
9.解:∵△ABC中,CD⊥AB于D,
∴∠ADC=90°.
∵E是AC的中点,DE=5,
∴AC=2DE=10.
∵AD=6,
∴CD===8.
故答案为:8.
10.解:∵四边形EFGH是正方形,
∴∠HEF=90°,
∴∠AEB=90°,
∵AB=13,AE=5,∠AEB=90°,
∴BE===12,
∵△ABE≌△BCF,
∴BF=AE,
∴EF=BE﹣BF=BE﹣AE=7,
∴EG=EF=7,
故答案为:7.
11.解:∵,
∴此三角形是直角三角形,
∴三角形的面积=,
故答案为:.
12.解:观察前4组数据的规律可知:第一个数是2(n+1);第二个是:n(n+2);第三个数是:(n+1)2+1.
所以第⑦组勾股数:16,63,65.
故答案为:16,63,65.
13.解:第一个数用字母n表示(n为偶数,且n≥4),则股:﹣1,弦:.
故答案是:.
14.解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB、AC长分别为13米、20米,AD的高度为12米,
∴BD=(米),DC=(米)
∴BC=BD+DC=5+16=21(米),
故答案为:21.
15.解:设竹子折断处离地面x尺,则斜边为(9﹣x)尺,
根据勾股定理得:x2+32=(9﹣x)2.
解得:x=4,
答:折断处离地面的高度为4尺.
故答案为:4.
16.解:设门高AB为x尺,则门的宽为(x﹣6.8)尺,AC=1丈=10尺,
依题意得:AB2+BC2=AC2,
即(x﹣6.8)2+x2=102.
故答案为:(x﹣6.8)2+x2=102.
三.解答题(共9小题,满分56分)
17.解:(1)在Rt△ABC中,由勾股定理得:BC===4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t=;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
18.解:(1)∵CD⊥AB,
∴∠ADC=90°,
∴AD===;
(2)证明:由上题知AD=,
同理可得BD=,
∴AB=AD+BD=5,
∵32+42=52,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
19.解:(1)∵在Rt△ABC中,∠C=90°,a=5,b=4,
∴c===;
(2)当边长为5的边是斜边时,第三边的长度为:=3;
当边长为5的边是直角边时,第三边的长度为:=;
综上所述,第三边的长度为3或.
20.(1)证明:∵∠ACB=90°,BC=12米,AB=13米,
∴AC===5(米),
∵CD=3米,AD=4米,
∴AD2+CD2=AC2=25,
∴∠ADC=90°;
(2)解:图中阴影部分土地的面积=A×BC﹣AD×CD=×5×12﹣×4×3=24(平方米).
21.解:设AB=x,则AC=x+1,
由图可得,∠ABC=90°,BC=5,
∴Rt△ABC中,AB2+BC2=AC2,
即x2+52=(x+1)2,
解得x=12,
答:风筝距离地面的高度AB为12米.
22.(1)证明:∵AC的垂直平分线交AC于点D,
∴AE=CE=3,
∵BC=8,
∴BE=5,
∵32+42=52,
∴△ABE是直角三角形;
(2)4×3÷2×2÷5×3÷2
=6×2÷5×3÷2
=2.4×3÷2
=3.6.
故△ACE的面积是3.6.
23.解:(1)两组勾股数:6,8,10;9,12,15;
故答案为:6,8,10;9,12,15;
(2)证明:x2+y2=(2n)2+(n2﹣1)2
=4n2+n4﹣2n2+1
=n4+2n2+1
=(n2+1)2,
∴x,y,z为勾股数.
24.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2;
(2)由图可知:
(b﹣a)2=3,4×ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
一.选择题(共8小题,满分32分)
1.在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=5:3:2,③∠A=90°﹣∠B,④∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,AB=10,AC=13,AD⊥BC,垂足为D,M为AD上任一点,则MC2﹣MB2等于( )
A.23 B.46 C.65 D.69
3.已知:△ABC中,∠C=45°,D为BC边上一点,AD=AB,BD=2,BH⊥AD于H,BH延长线交AC于E,则CE的长为( )
A. B. C. D.1
4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如图,设直角三角形较长直角边长为a,较短直角边长为b.若大正方形面积是9,小正方形面积是1,则ab的值是( )
A.4 B.6 C.8 D.10
5.四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图),大正方形的面积为13,小正方形的面积为1,则组成弦图的每个小直角三角形的两个直角边和为( )
A.5 B.7 C.25 D.3
6.若一个三角形的三个外角之比为3:4:5,则该三角形为( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.等腰直角三角形
7.如图,在四边形ABCD中,AB=2,BC=2,CD=4,DA=2,且∠ABC=90°,则四边形ABCD的面积是( )
A.4 B.1+2 C.2+4 D.1+
8.如图,某公园内的一块草坪是长方形ABCD,已知AB=8m,BC=6m,公园管理处为了方便群众,沿AC修了一条近道,一个人从A到C走A﹣B﹣C比直接走AC多走了( )
A.2米 B.4米 C.6米 D.8米
二.填空题(共8小题,满分32分)
9.如图,△ABC中,CD⊥AB于D,AC=BC,E是AC的中点.若AD=6,DE=5,则CD的长等于 .
10.2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果AB=13,AE=5,则EG的长为 .
11.如果一个三角形的三边分别为1、、,则其面积为 .
12.观察下列各组勾股数,并寻找规律:
①4,3,5; ②6,8,10; ③8,15,17; ④10,24,26……
请根据你发现的规律写出第⑦组勾股数: .
13.我们学习了勾股定理的逆定理后,知道了勾股数的概念.观察下列勾股数:4、3、5;6、8、10;8、15、17;10、24、26;…,发现这些勾股数的第一个数都是偶数,且从4起再没有间断过.观察并利用上述勾股数的规律,若第一个数用字母n表示(n为偶数,且n≥4),则最大的数可以用含n的式子表示为 .
14.如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB、AC长分别为13米、20米,主梁AD的高度为12米,则固定点B、C之间的距离为 米.
15.《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC= 尺.
16.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 .
三.解答题(共8小题,满分56分)
17.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
18.如图所示,在△ABC中,CD⊥AB于D,AC=4,BC=3,CD=
(1)求AD的长;
(2)求证:△ABC是直角三角形.
19.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C所对的边.
(1)若a=5,b=4,求c的长;
(2)若三条边中有两条边的长分别为5和4,求第三条边的长.
20.如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.
(1)求证:∠ADC=90°;
(2)求图中阴影部分土地的面积.
21.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度AB.
22.如图,在△ABC中,AB=4,BC=8,AC的垂直平分线交AC于点D,交BC于点E,CE=3,连接AE.
(1)求证:△ABE是直角三角形;
(2)求△ACE的面积.
23.法国数学家费尔马早在17世纪就研究过形如x2+y2=z2的关系式,显然,满足这个关系式的x,y,z有无数组.当x,y,z都为正整数时,我们把这样的三个数x,y,z叫做勾股数.如,3,4,5就是一组勾股数.
(1)请你再写出两组勾股数: , ;
(2)古希腊的哲学家柏拉图曾指出:如果n表示大于1的整数,x=2n,y=n2﹣1,z=n2+1,那么,x,y,z为勾股数,请你加以证明.
24.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
参考答案
一.选择题(共8小题,满分32分)
1.解:①∵∠A+∠B=∠C,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形;
②∵∠A:∠B:∠C=5:3:2,
设∠A=5x,则∠B=3x,∠C=2x,
∴5x+2x+3x=180,
解得:x=18°,
∴∠5=18°×5=90°,
∴△ABC是直角三角形;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
∴△ABC是直角三角形;
④∵3∠C=2∠B=∠A,
∴∠A+∠B+∠C=∠A+∠A+∠A=180°,
∴∠A=()°,
∴△ABC为钝角三角形.
∴能确定△ABC是直角三角形的有①②③共3个,
故选:C.
2.解:在Rt△ABD和Rt△ADC中,
BD2=AB2﹣AD2,CD2=AC2﹣AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2﹣AD2+MD2,MC2=CD2+MD2=AC2﹣AD2+MD2,
∴MC2﹣MB2
=(AC2﹣AD2+MD2)﹣(AB2﹣AD2+MD2)
=AC2﹣AB2
=132﹣102
=69.
故选:D.
3.解:过点A作AM⊥BD于点M,过点E作EF⊥BC于点F,
∵AB=AD,AM⊥BC,
∴∠BAM=∠DAM,BM=DM,
∵BH⊥AD,
∴∠HBD+∠HDB=90°,
又∵∠HDB+∠MAD=90°,
∴∠HBD=∠MAD,
∴∠HBD=∠BAM=∠MAD,
∵∠C=45°,
∴∠MAC=∠FEC=45°,
∵∠AEB=∠C+∠EBC=45°+∠EBC,∠BAC=∠MAC+∠BAM=45°+∠BAM,
∴∠AEB=∠BAC,
∴AB=BE,
在△ABM和△BEF中,
,
∴△ABM≌△BEF(AAS),
∴EF=BM=1,
∴CE=EF=,
故选:A.
4.解:∵直角三角形较长直角边长为a,较短直角边长为b,大正方形面积是9,
∴a2+b2=9,
∵小正方形面积是1,
∴(a﹣b)2=1,
∴a2+b2﹣2ab=1,
∴9﹣2ab=1,
∴ab=4,
故选:A.
5.解:设直角三角形的两直角边为a、b,
由题意可得,ab×4=13﹣1,a2+b2=13,
∴ab=6,
∴(a+b)2=a2+2ab+b2=(a2+b2)+2ab=13+2×6=13+12=25,
∴a+b=5或a+b=﹣5(舍去),
故选:A.
6.解:设三角形的三个外角的度数分别为3x、4x、5x,
则3x+4x+5x=360°,
解得,x=30°,
∴三角形的三个外角的度数分别为90°、120°、150°,
对应的三个内角的度数分别为90°、60°、30°,
∴此三角形为直角三角形,
故选:A.
7.解:连接AC,
∵∠ABC=90°,AB=BC=2,
在直角三角形ABC中,AC2=AB2+BC2,
∴AC2=8,
又∵DC=4,AD=2,
∴DC2=16,AD2=24,
在三角形ACD中有:DC2+AC2=16+8=24=AD2,
∴三角形ACD是直角三角形,∠DCA=90°,
∴四边形ABCD的面积=三角形DCA的面积+三角形ABC的面积=DC×AC+AB×BC=×4×2+×2×2=4+2,
故选:C.
8.解:由勾股定理,得
捷径AC==10(m),
多走了8+6﹣10=4(m).
故选:B.
二.填空题(共8小题,满分32分)
9.解:∵△ABC中,CD⊥AB于D,
∴∠ADC=90°.
∵E是AC的中点,DE=5,
∴AC=2DE=10.
∵AD=6,
∴CD===8.
故答案为:8.
10.解:∵四边形EFGH是正方形,
∴∠HEF=90°,
∴∠AEB=90°,
∵AB=13,AE=5,∠AEB=90°,
∴BE===12,
∵△ABE≌△BCF,
∴BF=AE,
∴EF=BE﹣BF=BE﹣AE=7,
∴EG=EF=7,
故答案为:7.
11.解:∵,
∴此三角形是直角三角形,
∴三角形的面积=,
故答案为:.
12.解:观察前4组数据的规律可知:第一个数是2(n+1);第二个是:n(n+2);第三个数是:(n+1)2+1.
所以第⑦组勾股数:16,63,65.
故答案为:16,63,65.
13.解:第一个数用字母n表示(n为偶数,且n≥4),则股:﹣1,弦:.
故答案是:.
14.解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB、AC长分别为13米、20米,AD的高度为12米,
∴BD=(米),DC=(米)
∴BC=BD+DC=5+16=21(米),
故答案为:21.
15.解:设竹子折断处离地面x尺,则斜边为(9﹣x)尺,
根据勾股定理得:x2+32=(9﹣x)2.
解得:x=4,
答:折断处离地面的高度为4尺.
故答案为:4.
16.解:设门高AB为x尺,则门的宽为(x﹣6.8)尺,AC=1丈=10尺,
依题意得:AB2+BC2=AC2,
即(x﹣6.8)2+x2=102.
故答案为:(x﹣6.8)2+x2=102.
三.解答题(共9小题,满分56分)
17.解:(1)在Rt△ABC中,由勾股定理得:BC===4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t=;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
18.解:(1)∵CD⊥AB,
∴∠ADC=90°,
∴AD===;
(2)证明:由上题知AD=,
同理可得BD=,
∴AB=AD+BD=5,
∵32+42=52,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
19.解:(1)∵在Rt△ABC中,∠C=90°,a=5,b=4,
∴c===;
(2)当边长为5的边是斜边时,第三边的长度为:=3;
当边长为5的边是直角边时,第三边的长度为:=;
综上所述,第三边的长度为3或.
20.(1)证明:∵∠ACB=90°,BC=12米,AB=13米,
∴AC===5(米),
∵CD=3米,AD=4米,
∴AD2+CD2=AC2=25,
∴∠ADC=90°;
(2)解:图中阴影部分土地的面积=A×BC﹣AD×CD=×5×12﹣×4×3=24(平方米).
21.解:设AB=x,则AC=x+1,
由图可得,∠ABC=90°,BC=5,
∴Rt△ABC中,AB2+BC2=AC2,
即x2+52=(x+1)2,
解得x=12,
答:风筝距离地面的高度AB为12米.
22.(1)证明:∵AC的垂直平分线交AC于点D,
∴AE=CE=3,
∵BC=8,
∴BE=5,
∵32+42=52,
∴△ABE是直角三角形;
(2)4×3÷2×2÷5×3÷2
=6×2÷5×3÷2
=2.4×3÷2
=3.6.
故△ACE的面积是3.6.
23.解:(1)两组勾股数:6,8,10;9,12,15;
故答案为:6,8,10;9,12,15;
(2)证明:x2+y2=(2n)2+(n2﹣1)2
=4n2+n4﹣2n2+1
=n4+2n2+1
=(n2+1)2,
∴x,y,z为勾股数.
24.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2;
(2)由图可知:
(b﹣a)2=3,4×ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
