山西省太原第五高级中学校2022届高三上学期第四次模块诊断数学(文)试卷(Word版含答案)
文档属性
| 名称 | 山西省太原第五高级中学校2022届高三上学期第四次模块诊断数学(文)试卷(Word版含答案) | 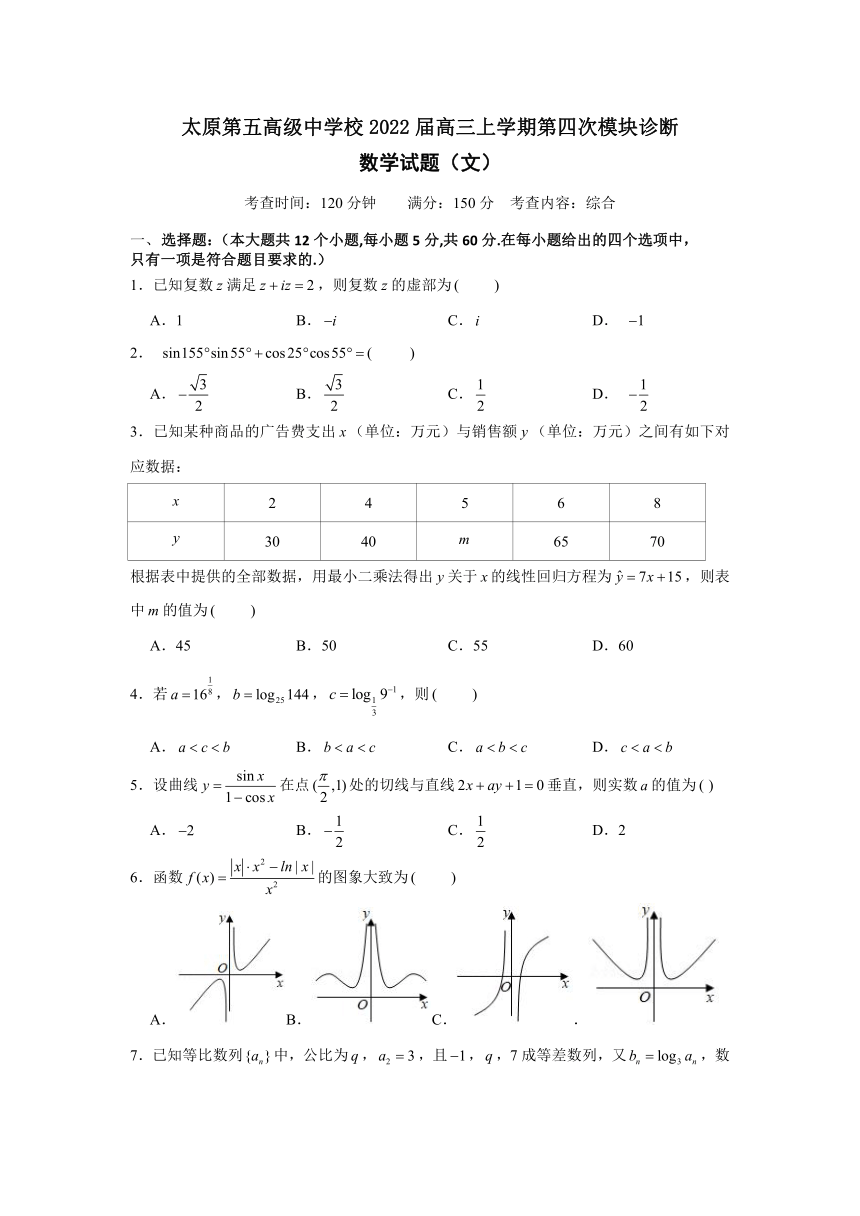 | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-05 18:47:42 | ||
图片预览





文档简介
太原第五高级中学校2022届高三上学期第四次模块诊断
数学试题(文)
考查时间:120分钟 满分:150分 考查内容:综合
1、 选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.已知复数满足,则复数的虚部为
A.1 B. C. D.
2.
A. B. C. D.
3.已知某种商品的广告费支出(单位:万元)与销售额(单位:万元)之间有如下对应数据:
2 4 5 6 8
30 40 65 70
根据表中提供的全部数据,用最小二乘法得出关于的线性回归方程为,则表中的值为
A.45 B.50 C.55 D.60
4.若,,,则
A. B. C. D.
5.设曲线在点处的切线与直线垂直,则实数的值为
A. B. C. D.2
6.函数的图象大致为
A.B.C..
7.已知等比数列中,公比为,,且,,7成等差数列,又,数列的前项和为,则
A.45 B.28 C.36 D.32
8.已知,是两个不同平面,,是两条不同直线,
①若,,,则;②若,,,则;
③若,,,则;④若,,,则.
在上述四个命题中,真命题的个数为
A.1 B.2 C.3 D.4
9.已知在中,,,点满足,则
A. B. C. D.
10.若函数在区间,上是增函数,且,,则函数在区间,上
A.是增函数 B.是减函数 C.可以取得最大值2 D.可以取得最小值
11.已知三棱锥中,,,的中点为,的中点恰好为点在平面上的射影,则该三棱锥外接球半径的平方为
A. B. C. D.
12.已知函数,.设函数,若函数有四个零点,则实数的取值范围是
A. B. C. D.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.郑州市2019年各月的平均气温数据的茎叶图如图:则这组数据的中位数是_____.
14.设为等差数列的前项和,已知在中只有最小,则 0.(填“”或“”或“”
15.如图所示,四棱锥的底面为正方形,底面,则下列结论中正确结论的序号是_________________.
①;②平面;③与平面所成的角等于与平面所成的角;④与所成的角等于与所成的角.
16.如图,在平面四边形中,,,,,,则的面积为 .
三、解答题(解答应写出文字说明、证明过程或演算步骤.)
17.(满分12分)已知在中,角,,所对的边分别为,,,且,.
(1)求角的大小;
(2)若,求的值.
18.(满分12分)今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员100人,其中50岁及以上的共有40人.这100人中确诊的有10名,其中50岁以下的人占.
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上 40
50岁以下
合计 10 100
(1)请将下面的列联表补充完整,并判断是否有95%的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,若从这5人中随机抽取3人,求恰有2人为50岁及以上的概率.
参考表
0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:,其中.
19.(满分12分)如图,三棱锥中,平面平面,,点在线段上,且,,点在线段上,且平面.
(1)证明:平面;
(2)若四棱锥的体积为7,求线段的长.
20.(满分12分)顺次连接椭圆的四个顶点得到边长为的菱形,该菱形对角线长度之比为
(1)求椭圆的标准方程;
(2)设椭圆的右焦点为,定点,过点的直线与椭圆交于两点,,设直线的斜率分别为,求证:为定值.
21.(满分12分)已知函数.
(1)求的单调区间;
(2)若不等式对恒成立,求的取值范围.
[选修4-4:极坐标参数方程](本小题满分10分)
22.已知曲线的参数方程为为参数),曲线的参数方程为为参数),以直角坐标原点为极点,轴的正半轴为极轴建立极坐标系.
(1)求曲线和曲线的的极坐标方程;
(2)射线与曲线和曲线分别交于,,已知点,求的面积.
[选修4-5:不等式选讲](本小题满分10分)
23.已知,.
(1)当时,求不等式的解集;
(2)求(2)(3)的最小值.
高三年级第四次模块诊断数学(文)试题答案
一.选择题:(本大题共12小题,每小题5分,满分60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D B A C A D C B B C D A
二. 填空题:(本大题共4小题,每小题5分,满分20分)
13. 14. 15. ① ②③ 16.
三.解答题
17.(满分12分)
解:(1)可得:………1分
即:.………2分
由正弦定理可知:,,………4分
,,可得,………5分
是三角形内角,.………6分
(2),,由正弦定理可得,………7分
可得,可得,可得,………8分
,,………10分
.………12分
18.(满分12分)
解:(1)因为100人中确诊的有10名,其中50岁以下的人占,
所以所以50岁以下的确诊人数为4,50岁及以上的确诊人数为6.
因为50岁及以上的共有40人,
即50岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率为;
列联表补充如下,
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上 6 34 40
50岁以下 4 56 60
合计 10 90 100
………2分
则,………5分
所以没有的把握认为是否确诊患新冠肺炎与年龄有关.………6分
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,则抽取的5人中,有3人50岁及以上,分别记作;2人50岁以下,记作.………7分
从中任取3人,可能的不同结果有:
,共10种不同的情形,………9分
恰有两人50岁及以上的情况有,,共6中不同的情况,………11分
由于每种情况都是等可能的,∴恰有2人为50岁及以上的概率为.………12分
19.(满分12分)
解:(Ⅰ)由可知为等腰中边的中点,故,………1分
又平面平面,平面平面 ,平面 ,,………2分
平面,平面,………4分
又,// 所以平面.………6分
(Ⅱ)设,在直角三角形中,,
,即, ………7分
// 知相似于,所以,
由得,………8分
从而四边形的面积为,………9分
由(Ⅰ)可知是四棱锥的高,,
所以,………10分
所以,所以或,
所以或.………12分
20.(满分12分)
解:(1)依题意,………1分
解得,………3分
所以椭圆的标准方程为.………4分
(2)当直线的斜率不存在时,直线,的倾斜角互补,所以.………5分
当直线的斜率存在时,设其方程为,
代入椭圆的方程,整理得,………7分
设,则,………8分
,
,………9分
因为,
,………11分
所以.………12分
21.(满分12分)
解:(1),………2分
令,得,则的单调递增区间为,;………3分
令,得,则的单调递减区间为;………4分
(2)当时,不等式,即,显然成立,………6分
当时,不等式对恒成立,等价于对恒成立,………7分
设,,………8分
令,得,………9分
令,得,且,………10分
所以,………11分
所以,即的取值范围为,.………12分
22.(满分10分)
解:(1)曲线的参数方程为为参数),由于①,,②,
1 ②得:.根据整理得.………3分
曲线的参数方程为为参数),转换为普通方程为.转换为极坐标方程为.………5分
(2)射线与曲线和曲线分别交于,,所以,………7分
,………9分
所以,则的面积为.………10分
23.(满分10分)
解:(1)当时,
.………2分
,或,
或,………4分
,
不等式的解集为.………5分
(2)(2)(3)
,………7分
关于的函数(2)(3)在上单的递减,在上单的递增,………9分
当时,(2)(3)的最小值为.………10分
数学试题(文)
考查时间:120分钟 满分:150分 考查内容:综合
1、 选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.已知复数满足,则复数的虚部为
A.1 B. C. D.
2.
A. B. C. D.
3.已知某种商品的广告费支出(单位:万元)与销售额(单位:万元)之间有如下对应数据:
2 4 5 6 8
30 40 65 70
根据表中提供的全部数据,用最小二乘法得出关于的线性回归方程为,则表中的值为
A.45 B.50 C.55 D.60
4.若,,,则
A. B. C. D.
5.设曲线在点处的切线与直线垂直,则实数的值为
A. B. C. D.2
6.函数的图象大致为
A.B.C..
7.已知等比数列中,公比为,,且,,7成等差数列,又,数列的前项和为,则
A.45 B.28 C.36 D.32
8.已知,是两个不同平面,,是两条不同直线,
①若,,,则;②若,,,则;
③若,,,则;④若,,,则.
在上述四个命题中,真命题的个数为
A.1 B.2 C.3 D.4
9.已知在中,,,点满足,则
A. B. C. D.
10.若函数在区间,上是增函数,且,,则函数在区间,上
A.是增函数 B.是减函数 C.可以取得最大值2 D.可以取得最小值
11.已知三棱锥中,,,的中点为,的中点恰好为点在平面上的射影,则该三棱锥外接球半径的平方为
A. B. C. D.
12.已知函数,.设函数,若函数有四个零点,则实数的取值范围是
A. B. C. D.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.郑州市2019年各月的平均气温数据的茎叶图如图:则这组数据的中位数是_____.
14.设为等差数列的前项和,已知在中只有最小,则 0.(填“”或“”或“”
15.如图所示,四棱锥的底面为正方形,底面,则下列结论中正确结论的序号是_________________.
①;②平面;③与平面所成的角等于与平面所成的角;④与所成的角等于与所成的角.
16.如图,在平面四边形中,,,,,,则的面积为 .
三、解答题(解答应写出文字说明、证明过程或演算步骤.)
17.(满分12分)已知在中,角,,所对的边分别为,,,且,.
(1)求角的大小;
(2)若,求的值.
18.(满分12分)今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员100人,其中50岁及以上的共有40人.这100人中确诊的有10名,其中50岁以下的人占.
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上 40
50岁以下
合计 10 100
(1)请将下面的列联表补充完整,并判断是否有95%的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,若从这5人中随机抽取3人,求恰有2人为50岁及以上的概率.
参考表
0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:,其中.
19.(满分12分)如图,三棱锥中,平面平面,,点在线段上,且,,点在线段上,且平面.
(1)证明:平面;
(2)若四棱锥的体积为7,求线段的长.
20.(满分12分)顺次连接椭圆的四个顶点得到边长为的菱形,该菱形对角线长度之比为
(1)求椭圆的标准方程;
(2)设椭圆的右焦点为,定点,过点的直线与椭圆交于两点,,设直线的斜率分别为,求证:为定值.
21.(满分12分)已知函数.
(1)求的单调区间;
(2)若不等式对恒成立,求的取值范围.
[选修4-4:极坐标参数方程](本小题满分10分)
22.已知曲线的参数方程为为参数),曲线的参数方程为为参数),以直角坐标原点为极点,轴的正半轴为极轴建立极坐标系.
(1)求曲线和曲线的的极坐标方程;
(2)射线与曲线和曲线分别交于,,已知点,求的面积.
[选修4-5:不等式选讲](本小题满分10分)
23.已知,.
(1)当时,求不等式的解集;
(2)求(2)(3)的最小值.
高三年级第四次模块诊断数学(文)试题答案
一.选择题:(本大题共12小题,每小题5分,满分60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D B A C A D C B B C D A
二. 填空题:(本大题共4小题,每小题5分,满分20分)
13. 14. 15. ① ②③ 16.
三.解答题
17.(满分12分)
解:(1)可得:………1分
即:.………2分
由正弦定理可知:,,………4分
,,可得,………5分
是三角形内角,.………6分
(2),,由正弦定理可得,………7分
可得,可得,可得,………8分
,,………10分
.………12分
18.(满分12分)
解:(1)因为100人中确诊的有10名,其中50岁以下的人占,
所以所以50岁以下的确诊人数为4,50岁及以上的确诊人数为6.
因为50岁及以上的共有40人,
即50岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率为;
列联表补充如下,
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上 6 34 40
50岁以下 4 56 60
合计 10 90 100
………2分
则,………5分
所以没有的把握认为是否确诊患新冠肺炎与年龄有关.………6分
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,则抽取的5人中,有3人50岁及以上,分别记作;2人50岁以下,记作.………7分
从中任取3人,可能的不同结果有:
,共10种不同的情形,………9分
恰有两人50岁及以上的情况有,,共6中不同的情况,………11分
由于每种情况都是等可能的,∴恰有2人为50岁及以上的概率为.………12分
19.(满分12分)
解:(Ⅰ)由可知为等腰中边的中点,故,………1分
又平面平面,平面平面 ,平面 ,,………2分
平面,平面,………4分
又,// 所以平面.………6分
(Ⅱ)设,在直角三角形中,,
,即, ………7分
// 知相似于,所以,
由得,………8分
从而四边形的面积为,………9分
由(Ⅰ)可知是四棱锥的高,,
所以,………10分
所以,所以或,
所以或.………12分
20.(满分12分)
解:(1)依题意,………1分
解得,………3分
所以椭圆的标准方程为.………4分
(2)当直线的斜率不存在时,直线,的倾斜角互补,所以.………5分
当直线的斜率存在时,设其方程为,
代入椭圆的方程,整理得,………7分
设,则,………8分
,
,………9分
因为,
,………11分
所以.………12分
21.(满分12分)
解:(1),………2分
令,得,则的单调递增区间为,;………3分
令,得,则的单调递减区间为;………4分
(2)当时,不等式,即,显然成立,………6分
当时,不等式对恒成立,等价于对恒成立,………7分
设,,………8分
令,得,………9分
令,得,且,………10分
所以,………11分
所以,即的取值范围为,.………12分
22.(满分10分)
解:(1)曲线的参数方程为为参数),由于①,,②,
1 ②得:.根据整理得.………3分
曲线的参数方程为为参数),转换为普通方程为.转换为极坐标方程为.………5分
(2)射线与曲线和曲线分别交于,,所以,………7分
,………9分
所以,则的面积为.………10分
23.(满分10分)
解:(1)当时,
.………2分
,或,
或,………4分
,
不等式的解集为.………5分
(2)(2)(3)
,………7分
关于的函数(2)(3)在上单的递减,在上单的递增,………9分
当时,(2)(3)的最小值为.………10分
同课章节目录
