【人教八上数学教学课件】14.1.4 第5课时 单项式除以单项式(共16张PPT)
文档属性
| 名称 | 【人教八上数学教学课件】14.1.4 第5课时 单项式除以单项式(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 19:44:56 | ||
图片预览






文档简介
(共16张PPT)
第十四章 整式的乘法与因式分解
14.1.4 第5课时 单项式除以单项式
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
学校后院的东花坛形状是长方形:
(1)如果它的长4
(2)如果它的面积是12
试一试:
3a2·( )=6a3b2c
( )·7x2y3=-x3y7
6a3b2c÷3a2=
-x3y7÷7x2y3=
利用乘法和除法互为逆运算的关系:
观察结果中的系数,字母及字母的次数有何规律?
获取新知
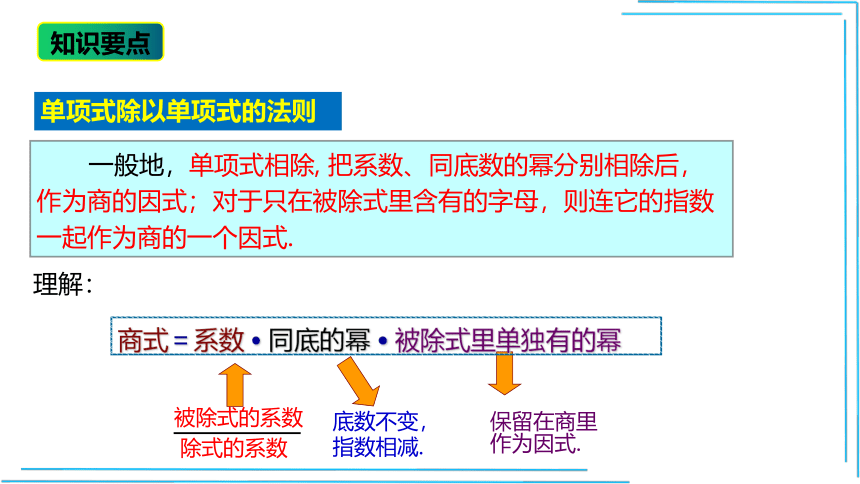
知识要点
一般地,单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式.
单项式除以单项式的法则
底数不变,
指数相减.
保留在商里
作为因式.
被除式的系数
除式的系数
理解:
商式=系数 同底的幂 被除式里单独有的幂
例题讲解
例1 计算
⑴ 24a3b2÷3ab2
解:(1)原式=(24÷3) (a3÷a) (b2÷b2)
=8a3-1·1
=8a2
注意:b2÷b2=1
(2)28x4y2 ÷7x3y;
(3)-5a5b3c ÷15a4b.
=4xy;
(2)原式=(-5÷15)a5-4b3-1c
解:(1)原式=(28 ÷7)x4-3y2-1
= ab2c.
针对训练
计算
(1)(2a2b2c)4z÷(-2ab2c2)2; (2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
方法总结:掌握整式的除法的运算法则是解题的关键,注意在计算过程中,有乘方的先算乘方,再算乘除.
单项式除以单项式的“三注意”
(1)系数相除作为商的系数,系数包括前面的符号,应先确定
商的符号;
(2)含有相同字母的部分按同底数幂的除法法则进行运算,即
底数不变,指数相减;
(3)单独在被除式中出现的字母不能漏掉,要连同它的指数直
接作为商的一个因式.
归纳总结
1.计算:
(1)6a3÷2a2; (2)24a2b3÷3ab;
(3)-21a2b3c÷3ab;
解:(1) 6a3÷2a2
=(6÷2)(a3÷a2)
=3a.
(2) 24a2b3÷3ab
=(24÷3)a2-1b3-1
=8ab2.
(3)-21a2b3c÷3ab
=(-21÷3)a2-1b3-1c
= -7ab2c;
随堂演练
2.计算:
(2) 12(a-b)5÷3(a-b)2
=(12÷3)(a-b)5-2
=4(a-b)3
解:(1)
注意:将(a-b)看作一个整体
(3)
注意变号技巧:变偶不变奇
课堂小结
单项式除以单项式的法则
单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式.
https://www.21cnjy.com/help/help_extract.php
第十四章 整式的乘法与因式分解
14.1.4 第5课时 单项式除以单项式
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
学校后院的东花坛形状是长方形:
(1)如果它的长4
(2)如果它的面积是12
试一试:
3a2·( )=6a3b2c
( )·7x2y3=-x3y7
6a3b2c÷3a2=
-x3y7÷7x2y3=
利用乘法和除法互为逆运算的关系:
观察结果中的系数,字母及字母的次数有何规律?
获取新知
知识要点
一般地,单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式.
单项式除以单项式的法则
底数不变,
指数相减.
保留在商里
作为因式.
被除式的系数
除式的系数
理解:
商式=系数 同底的幂 被除式里单独有的幂
例题讲解
例1 计算
⑴ 24a3b2÷3ab2
解:(1)原式=(24÷3) (a3÷a) (b2÷b2)
=8a3-1·1
=8a2
注意:b2÷b2=1
(2)28x4y2 ÷7x3y;
(3)-5a5b3c ÷15a4b.
=4xy;
(2)原式=(-5÷15)a5-4b3-1c
解:(1)原式=(28 ÷7)x4-3y2-1
= ab2c.
针对训练
计算
(1)(2a2b2c)4z÷(-2ab2c2)2; (2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
方法总结:掌握整式的除法的运算法则是解题的关键,注意在计算过程中,有乘方的先算乘方,再算乘除.
单项式除以单项式的“三注意”
(1)系数相除作为商的系数,系数包括前面的符号,应先确定
商的符号;
(2)含有相同字母的部分按同底数幂的除法法则进行运算,即
底数不变,指数相减;
(3)单独在被除式中出现的字母不能漏掉,要连同它的指数直
接作为商的一个因式.
归纳总结
1.计算:
(1)6a3÷2a2; (2)24a2b3÷3ab;
(3)-21a2b3c÷3ab;
解:(1) 6a3÷2a2
=(6÷2)(a3÷a2)
=3a.
(2) 24a2b3÷3ab
=(24÷3)a2-1b3-1
=8ab2.
(3)-21a2b3c÷3ab
=(-21÷3)a2-1b3-1c
= -7ab2c;
随堂演练
2.计算:
(2) 12(a-b)5÷3(a-b)2
=(12÷3)(a-b)5-2
=4(a-b)3
解:(1)
注意:将(a-b)看作一个整体
(3)
注意变号技巧:变偶不变奇
课堂小结
单项式除以单项式的法则
单项式相除, 把系数、同底数的幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连它的指数一起作为商的一个因式.
https://www.21cnjy.com/help/help_extract.php
