2021-2022学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 289.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 09:00:42 | ||
图片预览




文档简介
2021-2022学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷
一.选择题
1.对于几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( )
A.③⑤⑥ B.①②③ C.④⑤ D.④⑥
2.一个直棱柱有12个顶点,那么它的面的个数是( )
A.10个 B.9个 C.8个 D.7个
3.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支 B.21支 C.22支 D.25支
4.一个圆的直径是20厘米,它的周长是( )厘米.
A.20π B.10π C.100π D.400π
5.在五棱柱、圆柱、圆锥和正方体这四个几何体中,侧面展开图是长方形的有( )
A.1个 B.2个 C.3个 D.4个
6.一个正方体的每个面都有一个汉字,其平面展开图如图,那么在该正方体中和“毒”字相对的字是( )
A.卫 B.防 C.讲 D.生
7.下面七个几何体中,是棱柱的有( )个.
A.4 B.3 C.2 D.1
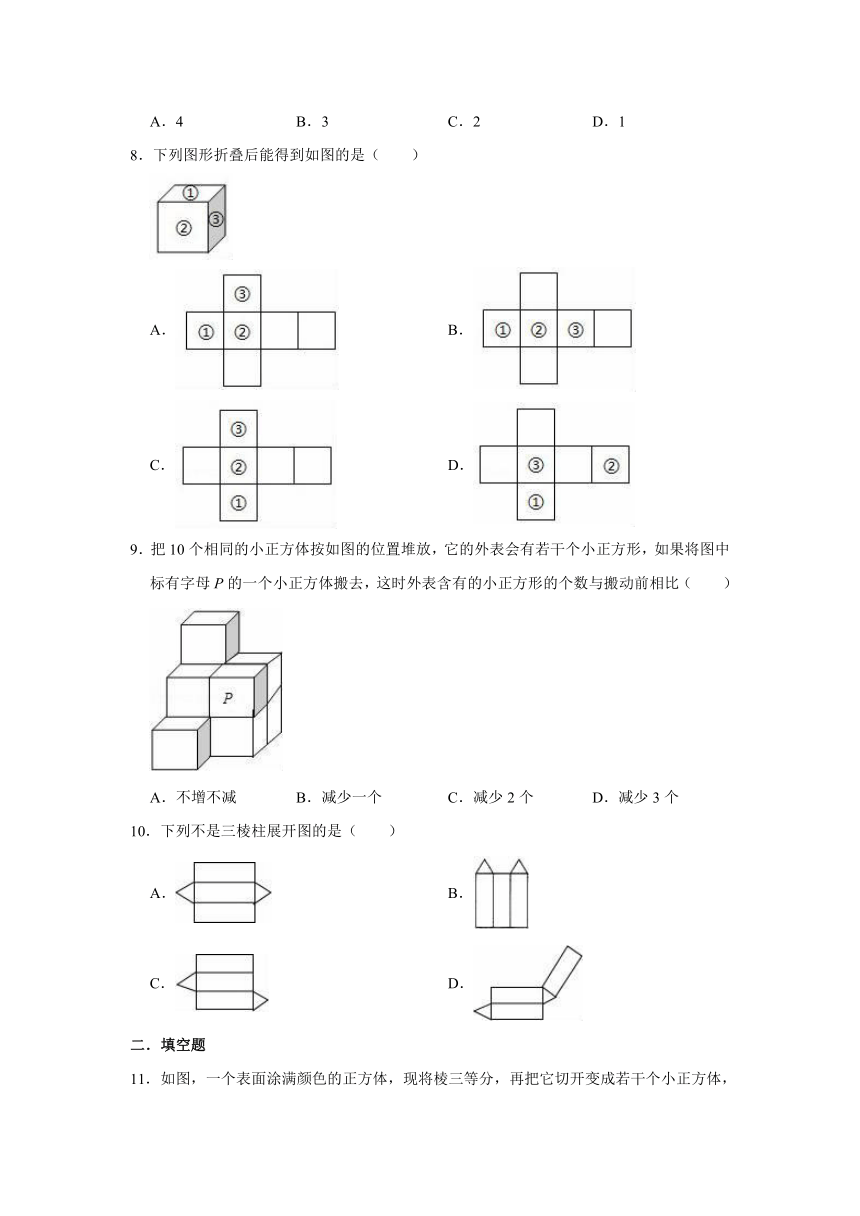
8.下列图形折叠后能得到如图的是( )
A. B.
C. D.
9.把10个相同的小正方体按如图的位置堆放,它的外表会有若干个小正方形,如果将图中标有字母P的一个小正方体搬去,这时外表含有的小正方形的个数与搬动前相比( )
A.不增不减 B.减少一个 C.减少2个 D.减少3个
10.下列不是三棱柱展开图的是( )
A. B.
C. D.
二.填空题
11.如图,一个表面涂满颜色的正方体,现将棱三等分,再把它切开变成若干个小正方体,两面都涂色的有 个;各面都没有涂色的有 个.
12.如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的 倍.
13.现在新型肺炎正在世界各地肆虐,WHO将它命名为冠状病毒2019(HCoV﹣19).它的形状是一个球体,体积大约288000πnm3,则它的直径约是 nm.(球的体积公式V=)
14.一个棱柱有18条棱,则它有 个面.
15.如图所示的平面图形折叠后围成的立体图形是 .
16.如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y= .
17.一个画家有14个棱长为1m的正方体,他在地面上把它们摆成如图的形状,然后他把露出的表面都涂上颜色,则被涂上颜色的部分面积为 m2.
18.将下列几何体分类,柱体有: ,锥体有 (填序号)
19.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .
20.一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为 cm3.
三.解答题
21.如图所示,请将下列几何体分类.
22.如图所示为8个立体图形.
其中,柱体的序号为 ,锥体的序号为 ,有曲面的序号为 .
23.如图.已知大圆的直径为4厘米,求图中空白部分的面积.
24.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
25.观察下列多面体,并把下表补充完整.
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数a 6 10 12
棱数b 9 12
面数c 5 8
观察上表中的结果,你能发现a、b、c之间有什么关系吗?请写出发现的关系式.
26.某种产品形状是长方体,长为8cm,它的展开图如图:
(1)求长方体的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装10件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小).
27.棱长为a的正方体,摆放成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
参考答案与试题解析
一.选择题
1.解:①②④属于平面图形,③⑤⑥属于立体图形.
故选:A.
2.解:直棱柱有12个顶点,一定是六棱柱,
所以它有6个侧面和2个底面共8个面.
故选:C.
3.解:若按如图方法摆放,
则△ABC为等腰三角形,其高为AD,
则AB=0.8=,BD=0.4+=,
由勾股定理,得AD=≈0.65276,
∵0.8+4×0.65276=3.411>3.4,这种情况不可能,
这样有4个高<2.8+0.4+0.4<3.6,最后还剩下0.9×3.4还可以放4支.
这样,长放0.4+(4个<0.7)+0.4+0.8<4.4<4.5,
宽放4个0.8=3.2<3.4,共4+3+4+3+4+4=22支(如图).
故选:C.
4.解:由题可得,圆周长是20π.
故选:A.
5.解:五棱柱的侧面展开图是长方形;
圆柱侧面展开图是长方形;
圆锥侧面展开图是扇形;
正方体侧面展开图是4个正方形组成的长方形.
故侧面展开图是长方形的共有3个.
故选:C.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“讲”与“生”是相对面,
“卫”与“病”是相对面,
“防”与“毒”是相对面.
故选:B.
7.解:如图,根据棱柱的特征可得,
①是三棱柱,②是球,③圆锥,④三棱锥,⑤正方体,⑥圆柱体,⑦六棱柱,
因此棱柱有:①⑤⑦,
故选:B.
8.解:A.折叠后①,②,③相邻,故此选项正确;
B.折叠后①与③是相对面,不可能是①,②,③相邻,故此选项错误;
C.折叠后①与③是相对面,不可能是①,②,③相邻,故此选项错误;
D.折叠后②与③是相对面,不可能是①,②,③相邻,故此选项错误.
故选:A.
9.解:考查图形可知:搬去标有字母P的一个小正方体的表面积和搬动前比较,搬动后立方体的表面积减少了三个小正方形,又增加了三个小正方形.故不增不减.
故选:A.
10.解:A、C、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.
B围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故B不能围成三棱柱.
故选:B.
二.填空题
11.解:两面都涂色是中间那层,边上的部分共有12个
各面都没有涂色的只有最中间那个,所以只有一个.
故答案为:12;1.
12.解:设圆的半径为r,则它的面积为πr2,
如果圆的半径长扩大为原来的3倍,则半径为3r,则它的面积为π(3r)2=9πr2,
∴如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的9倍.
故答案为:9
13.解:由题意,得=288000π.
解得R=60.
故它的直径是120nm.
故答案是:120
14.解:一个棱柱有18条棱,这是一个六棱柱,它有8个面.
故答案为:8.
15.解:三个长方形和两个三角形折叠后能围成直三棱柱.
16.解:∵“4”与“y”是对面,“x”与“2”是对面,
∴x=6,y=4.
∴x+y=10.
故答案为:10.
17.解:从上面看到的面积是9个正方形的面积,前后左右共看到6×4=24个正方形的面积,所以被涂上颜色的总面积为24+9=33m2.
故答案为33.
18.解:柱体分为圆柱和棱柱,所以柱体有:(1)(2)(3);锥体包括圆柱与圆锥,所以锥体有(5)(6),球属于单独的一类.
故答案为柱体有(1)(2)(3);锥体有(5)(6).
19.解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
20.解:20﹣15=5(cm),
15﹣5=10(cm),
26﹣10=16(cm),
16×10×5=800(cm3).
答:其容积为800cm3.
故答案为:800.
三.解答题
21.解:方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体;(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面;(4)是一类,只有曲面.
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:如图,通过割补法,空白部分的面积可以转化为正方形ACBD的面积,
S正方形ACBD=AB CD=×4×4=8(cm2),
答:图中空白部分的面积为8cm2.
24.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
25.解:填表如下:
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数a 6 8 10 12
棱数b 9 12 15 18
面数c 5 6 7 8
观察上表中的结果,能发现a、b、c之间有的关系是:a+c﹣b=2.
26.解:(1)设长方体的高为xcm,则长方形的宽为(12﹣2x)cm,根据题意可得:
12﹣2x+8+x+8=25,
解得:x=3,
所以长方体的高为3cm,宽为6cm,长为8cm,
长方体的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装10件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,10件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×12×8规格,该产品的侧面积分别为:
8×12=96(cm2),
8×15=120(cm2)
12×15=180(cm2)
纸箱的表面积为:(120+96+180)×2=792(cm2).
27.解:(1)6×(1+2+3) a2=36a2.
故该物体的表面积为36a2;
(2)6×(1+2+3+…+20) a2=1260a2.
故该物体的表面积为1260a2.
一.选择题
1.对于几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( )
A.③⑤⑥ B.①②③ C.④⑤ D.④⑥
2.一个直棱柱有12个顶点,那么它的面的个数是( )
A.10个 B.9个 C.8个 D.7个
3.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支 B.21支 C.22支 D.25支
4.一个圆的直径是20厘米,它的周长是( )厘米.
A.20π B.10π C.100π D.400π
5.在五棱柱、圆柱、圆锥和正方体这四个几何体中,侧面展开图是长方形的有( )
A.1个 B.2个 C.3个 D.4个
6.一个正方体的每个面都有一个汉字,其平面展开图如图,那么在该正方体中和“毒”字相对的字是( )
A.卫 B.防 C.讲 D.生
7.下面七个几何体中,是棱柱的有( )个.
A.4 B.3 C.2 D.1
8.下列图形折叠后能得到如图的是( )
A. B.
C. D.
9.把10个相同的小正方体按如图的位置堆放,它的外表会有若干个小正方形,如果将图中标有字母P的一个小正方体搬去,这时外表含有的小正方形的个数与搬动前相比( )
A.不增不减 B.减少一个 C.减少2个 D.减少3个
10.下列不是三棱柱展开图的是( )
A. B.
C. D.
二.填空题
11.如图,一个表面涂满颜色的正方体,现将棱三等分,再把它切开变成若干个小正方体,两面都涂色的有 个;各面都没有涂色的有 个.
12.如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的 倍.
13.现在新型肺炎正在世界各地肆虐,WHO将它命名为冠状病毒2019(HCoV﹣19).它的形状是一个球体,体积大约288000πnm3,则它的直径约是 nm.(球的体积公式V=)
14.一个棱柱有18条棱,则它有 个面.
15.如图所示的平面图形折叠后围成的立体图形是 .
16.如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y= .
17.一个画家有14个棱长为1m的正方体,他在地面上把它们摆成如图的形状,然后他把露出的表面都涂上颜色,则被涂上颜色的部分面积为 m2.
18.将下列几何体分类,柱体有: ,锥体有 (填序号)
19.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .
20.一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为 cm3.
三.解答题
21.如图所示,请将下列几何体分类.
22.如图所示为8个立体图形.
其中,柱体的序号为 ,锥体的序号为 ,有曲面的序号为 .
23.如图.已知大圆的直径为4厘米,求图中空白部分的面积.
24.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
25.观察下列多面体,并把下表补充完整.
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数a 6 10 12
棱数b 9 12
面数c 5 8
观察上表中的结果,你能发现a、b、c之间有什么关系吗?请写出发现的关系式.
26.某种产品形状是长方体,长为8cm,它的展开图如图:
(1)求长方体的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装10件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小).
27.棱长为a的正方体,摆放成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
参考答案与试题解析
一.选择题
1.解:①②④属于平面图形,③⑤⑥属于立体图形.
故选:A.
2.解:直棱柱有12个顶点,一定是六棱柱,
所以它有6个侧面和2个底面共8个面.
故选:C.
3.解:若按如图方法摆放,
则△ABC为等腰三角形,其高为AD,
则AB=0.8=,BD=0.4+=,
由勾股定理,得AD=≈0.65276,
∵0.8+4×0.65276=3.411>3.4,这种情况不可能,
这样有4个高<2.8+0.4+0.4<3.6,最后还剩下0.9×3.4还可以放4支.
这样,长放0.4+(4个<0.7)+0.4+0.8<4.4<4.5,
宽放4个0.8=3.2<3.4,共4+3+4+3+4+4=22支(如图).
故选:C.
4.解:由题可得,圆周长是20π.
故选:A.
5.解:五棱柱的侧面展开图是长方形;
圆柱侧面展开图是长方形;
圆锥侧面展开图是扇形;
正方体侧面展开图是4个正方形组成的长方形.
故侧面展开图是长方形的共有3个.
故选:C.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“讲”与“生”是相对面,
“卫”与“病”是相对面,
“防”与“毒”是相对面.
故选:B.
7.解:如图,根据棱柱的特征可得,
①是三棱柱,②是球,③圆锥,④三棱锥,⑤正方体,⑥圆柱体,⑦六棱柱,
因此棱柱有:①⑤⑦,
故选:B.
8.解:A.折叠后①,②,③相邻,故此选项正确;
B.折叠后①与③是相对面,不可能是①,②,③相邻,故此选项错误;
C.折叠后①与③是相对面,不可能是①,②,③相邻,故此选项错误;
D.折叠后②与③是相对面,不可能是①,②,③相邻,故此选项错误.
故选:A.
9.解:考查图形可知:搬去标有字母P的一个小正方体的表面积和搬动前比较,搬动后立方体的表面积减少了三个小正方形,又增加了三个小正方形.故不增不减.
故选:A.
10.解:A、C、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.
B围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故B不能围成三棱柱.
故选:B.
二.填空题
11.解:两面都涂色是中间那层,边上的部分共有12个
各面都没有涂色的只有最中间那个,所以只有一个.
故答案为:12;1.
12.解:设圆的半径为r,则它的面积为πr2,
如果圆的半径长扩大为原来的3倍,则半径为3r,则它的面积为π(3r)2=9πr2,
∴如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的9倍.
故答案为:9
13.解:由题意,得=288000π.
解得R=60.
故它的直径是120nm.
故答案是:120
14.解:一个棱柱有18条棱,这是一个六棱柱,它有8个面.
故答案为:8.
15.解:三个长方形和两个三角形折叠后能围成直三棱柱.
16.解:∵“4”与“y”是对面,“x”与“2”是对面,
∴x=6,y=4.
∴x+y=10.
故答案为:10.
17.解:从上面看到的面积是9个正方形的面积,前后左右共看到6×4=24个正方形的面积,所以被涂上颜色的总面积为24+9=33m2.
故答案为33.
18.解:柱体分为圆柱和棱柱,所以柱体有:(1)(2)(3);锥体包括圆柱与圆锥,所以锥体有(5)(6),球属于单独的一类.
故答案为柱体有(1)(2)(3);锥体有(5)(6).
19.解:由图1可得,“中”和“的”相对;“国”和“我”相对;“梦”和“梦”相对;
由图2可得,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格时,“国”在下面,则这时小正方体朝上一面的字是“我”.
故答案为:我.
20.解:20﹣15=5(cm),
15﹣5=10(cm),
26﹣10=16(cm),
16×10×5=800(cm3).
答:其容积为800cm3.
故答案为:800.
三.解答题
21.解:方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体;(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面;(4)是一类,只有曲面.
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:如图,通过割补法,空白部分的面积可以转化为正方形ACBD的面积,
S正方形ACBD=AB CD=×4×4=8(cm2),
答:图中空白部分的面积为8cm2.
24.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
25.解:填表如下:
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数a 6 8 10 12
棱数b 9 12 15 18
面数c 5 6 7 8
观察上表中的结果,能发现a、b、c之间有的关系是:a+c﹣b=2.
26.解:(1)设长方体的高为xcm,则长方形的宽为(12﹣2x)cm,根据题意可得:
12﹣2x+8+x+8=25,
解得:x=3,
所以长方体的高为3cm,宽为6cm,长为8cm,
长方体的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装10件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,10件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×12×8规格,该产品的侧面积分别为:
8×12=96(cm2),
8×15=120(cm2)
12×15=180(cm2)
纸箱的表面积为:(120+96+180)×2=792(cm2).
27.解:(1)6×(1+2+3) a2=36a2.
故该物体的表面积为36a2;
(2)6×(1+2+3+…+20) a2=1260a2.
故该物体的表面积为1260a2.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
