【人教九上数学最新教学课件】24.4 第2课时 圆锥的侧面积和全面积 课件(共14张PPT)
文档属性
| 名称 | 【人教九上数学最新教学课件】24.4 第2课时 圆锥的侧面积和全面积 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
24.4 第2课时 圆锥的侧面积和全面积
随堂演练
获取新知
例题讲解
第二十四章 圆
课堂小结
情景导入
情景导入
生活中的圆锥
获取新知
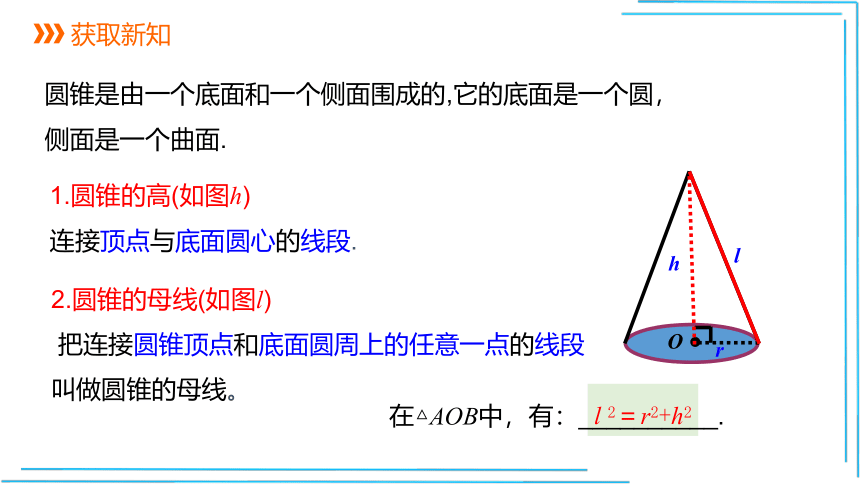
圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,
侧面是一个曲面.
2.圆锥的母线(如图l)
把连接圆锥顶点和底面圆周上的任意一点的线段叫做圆锥的母线。
1.圆锥的高(如图h)
连接顶点与底面圆心的线段.
O ●
r
h
l
l 2=r2+h2
在△AOB中,有:__________.
顶点
母线
底面半径
侧面
高
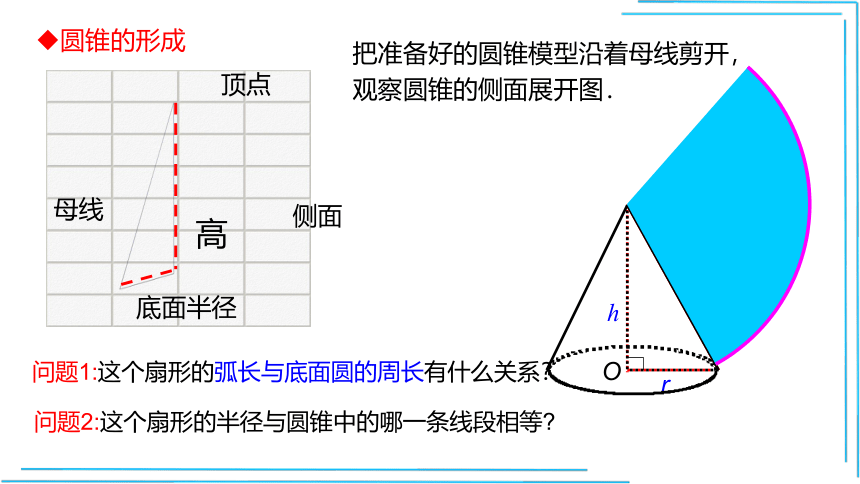
圆锥的形成
把准备好的圆锥模型沿着母线剪开,观察圆锥的侧面展开图.
h
r
O
问题1:这个扇形的弧长与底面圆的周长有什么关系?
问题2:这个扇形的半径与圆锥中的哪一条线段相等
A
B
O
C
1.圆锥的侧面展开图是扇形
2.其侧面展开图扇形的半径R=母线的长l
r
h
l
3.侧面展开图扇形的弧长=底面周长
S侧=πrl(r表示圆锥底面的半径, l表示圆锥的母线长 )圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
S全=S侧+S底=πrl+πr2
L
例题讲解
例 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20 个底面积为 12m2,高为 3.2m ,外围高1.8m 的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)?
h1
h2
r
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为12 m2,高h2=1.8 m;
上部圆锥的高h1=3.2-1.8=1.4(m).
圆柱的底面圆的半径r =
侧面积为2π×1.954×1.8≈22.10 (m2).
圆锥的母线长l=
侧面展开扇形的弧长为2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建20个这样的蒙古包至少需要毛毡
20×(22.10+14.76)≈738(m2).
h1
h2
r
随堂演练
1. 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
C
2.(1)已知一个圆锥的底面半径为12 cm,母线长为20 cm,则这个圆锥的侧面积为_______,全面积为______.
(2)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_____.
3.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h.
解:由题意,得 ,而r=2cm,
∴l=6cm,
∴由勾股定理,得
即该圆锥的高h为
课堂小结
重要图形
重要结论
r2+h2=l2
S侧=πrl.
S 全= S侧+ S底= πrl+πr2
圆锥的高
母线
r
S
A
O
B
h
l
o
侧面
展开图
r
底面
①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
https://www.21cnjy.com/help/help_extract.php
24.4 第2课时 圆锥的侧面积和全面积
随堂演练
获取新知
例题讲解
第二十四章 圆
课堂小结
情景导入
情景导入
生活中的圆锥
获取新知
圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,
侧面是一个曲面.
2.圆锥的母线(如图l)
把连接圆锥顶点和底面圆周上的任意一点的线段叫做圆锥的母线。
1.圆锥的高(如图h)
连接顶点与底面圆心的线段.
O ●
r
h
l
l 2=r2+h2
在△AOB中,有:__________.
顶点
母线
底面半径
侧面
高
圆锥的形成
把准备好的圆锥模型沿着母线剪开,观察圆锥的侧面展开图.
h
r
O
问题1:这个扇形的弧长与底面圆的周长有什么关系?
问题2:这个扇形的半径与圆锥中的哪一条线段相等
A
B
O
C
1.圆锥的侧面展开图是扇形
2.其侧面展开图扇形的半径R=母线的长l
r
h
l
3.侧面展开图扇形的弧长=底面周长
S侧=πrl(r表示圆锥底面的半径, l表示圆锥的母线长 )圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
S全=S侧+S底=πrl+πr2
L
例题讲解
例 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20 个底面积为 12m2,高为 3.2m ,外围高1.8m 的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)?
h1
h2
r
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为12 m2,高h2=1.8 m;
上部圆锥的高h1=3.2-1.8=1.4(m).
圆柱的底面圆的半径r =
侧面积为2π×1.954×1.8≈22.10 (m2).
圆锥的母线长l=
侧面展开扇形的弧长为2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建20个这样的蒙古包至少需要毛毡
20×(22.10+14.76)≈738(m2).
h1
h2
r
随堂演练
1. 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
C
2.(1)已知一个圆锥的底面半径为12 cm,母线长为20 cm,则这个圆锥的侧面积为_______,全面积为______.
(2)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_____.
3.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h.
解:由题意,得 ,而r=2cm,
∴l=6cm,
∴由勾股定理,得
即该圆锥的高h为
课堂小结
重要图形
重要结论
r2+h2=l2
S侧=πrl.
S 全= S侧+ S底= πrl+πr2
圆锥的高
母线
r
S
A
O
B
h
l
o
侧面
展开图
r
底面
①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
https://www.21cnjy.com/help/help_extract.php
同课章节目录
