5.3 三角形的中位线 课件(共17张PPT)
文档属性
| 名称 | 5.3 三角形的中位线 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 19:15:12 | ||
图片预览



文档简介
(共17张PPT)
第五章 平行四边形
3 三角形的中位线
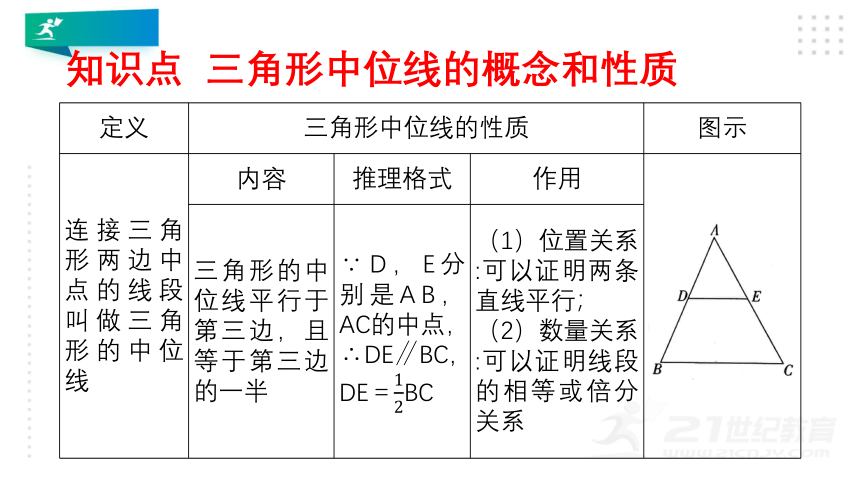
知识点 三角形中位线的概念和性质
定义 三角形中位线的性质 图示
连接三角形两边中点的线段叫做三角形的中位线 内容 推理格式 作用
三角形的中位线平行于第三边,且等于第三边的一半 ∵D,E分别是AB,AC的中点,∴DE∥BC,DE=BC (1)位置关系:可以证明两条直线平行; (2)数量关系:可以证明线段的相等或倍分关系
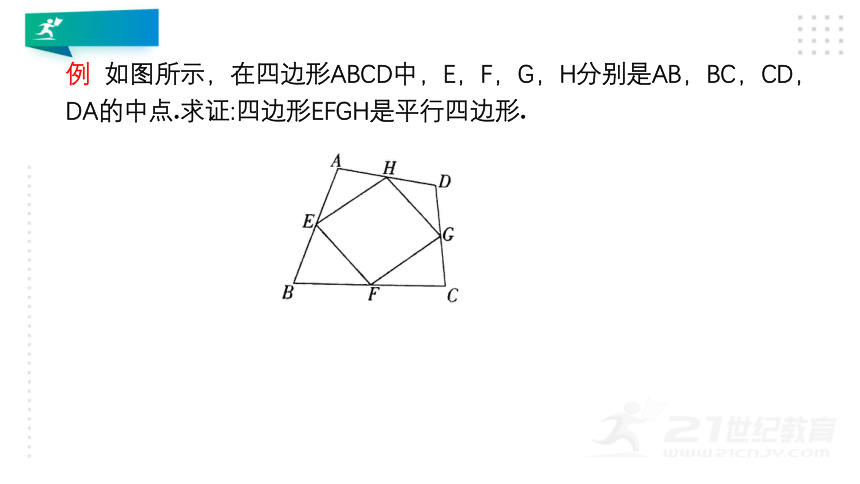
例 如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
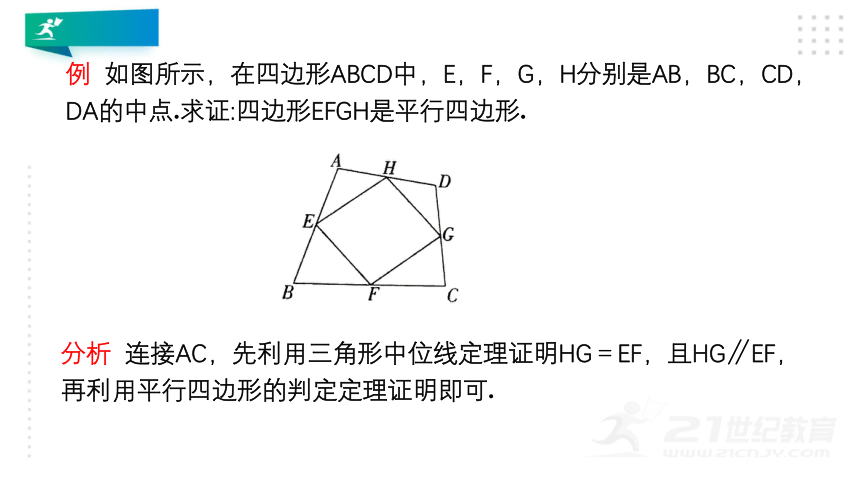
例 如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
分析 连接AC,先利用三角形中位线定理证明HG=EF,且HG∥EF,再利用平行四边形的判定定理证明即可.
证明 如图所示,连接AC.
∵G,H分别是CD,DA的中点,∴HG∥AC,HG=AC.
同理,EF∥AC,EF= AC.∴HG∥EF,HG=EF.
∴四边形EFGH是平行四边形.
方法归纳
当题目中出现线段的中点时,一般连接中点,考虑用三角形的中位线定理来解决,本题还可以再连接BD,利用两组对边分别平行的四边形是平行四边形来解决.
经典例题
题型一 三角形中位线性质的应用
例1 如图所示,在△ABC中,E是AB的中点,CD平分∠ACB,AD⊥CD于点D,连接ED,求证:
(1)DE∥BC;
(2)2DE=BC-AC.
分析 (1)延长AD交BC于点F,根据△ACD≌△FCD得到AC=CF,AD=DF,故可得出DE∥BC.
(2)根据AC=CF可得出BF=BC-CF=BC-AC,由三角形中位线定理即可得出结论.
证明 (1)如图所示,延长AD交BC于点F,
∵CD平分∠ACB,且AD⊥CD,∴∠CDA=∠CDF=90°,∠ACD=∠FCD.
又∵CD=CD,∴△ACD≌△FCD,∴AC=CF,AD=DF.
∵E是AB的中点,∴DE是△ABF的中位线,∴DE∥BC.
(2)由(1)知DE是△ABF的中位线,AC=CF,
∴DE=BF= (BC-CF)= (BC-AC),即2DE=BC-AC.
点拨
当问题中有中点,且证明线段平行或2倍关系时,我们通常考虑问题能不能应用三角形中位线定理解决.
题型二 构造三角形的中位线解题
例2 如图所示,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,EF分别交BD、AC于点G、H.求证:OG=OH.
分析
取BC边的中点M,连接EM,FM,首先根据三角形的中位线定理得到△EMF是等腰三角形,然后根据等边对等角得到∠MEF=∠MFE,再根据平行线的性质得到∠OGH=∠OHG,最后根据等角对等边即可证得结论.
证明 如图所示,取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,∴MF∥BD,MF=BD,
同理,ME∥AC,ME= AC,
∵AC=BD,∴ME=MF,∴∠MEF=∠MFE.∵MF∥BD,∴∠MFE=∠OGH.
同理,∠MEF=∠OHG,∴∠OGH=∠OHG,∴OG=OH.
点拨
已知三角形一边的中点时,常作辅助线构造出三角形的中位线.
第五章 平行四边形
3 三角形的中位线
知识点 三角形中位线的概念和性质
定义 三角形中位线的性质 图示
连接三角形两边中点的线段叫做三角形的中位线 内容 推理格式 作用
三角形的中位线平行于第三边,且等于第三边的一半 ∵D,E分别是AB,AC的中点,∴DE∥BC,DE=BC (1)位置关系:可以证明两条直线平行; (2)数量关系:可以证明线段的相等或倍分关系
例 如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
例 如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
分析 连接AC,先利用三角形中位线定理证明HG=EF,且HG∥EF,再利用平行四边形的判定定理证明即可.
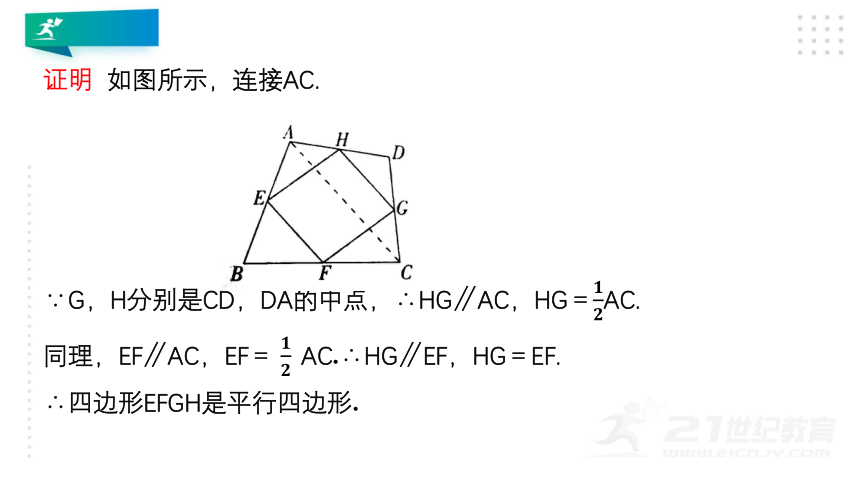
证明 如图所示,连接AC.
∵G,H分别是CD,DA的中点,∴HG∥AC,HG=AC.
同理,EF∥AC,EF= AC.∴HG∥EF,HG=EF.
∴四边形EFGH是平行四边形.
方法归纳
当题目中出现线段的中点时,一般连接中点,考虑用三角形的中位线定理来解决,本题还可以再连接BD,利用两组对边分别平行的四边形是平行四边形来解决.
经典例题
题型一 三角形中位线性质的应用
例1 如图所示,在△ABC中,E是AB的中点,CD平分∠ACB,AD⊥CD于点D,连接ED,求证:
(1)DE∥BC;
(2)2DE=BC-AC.
分析 (1)延长AD交BC于点F,根据△ACD≌△FCD得到AC=CF,AD=DF,故可得出DE∥BC.
(2)根据AC=CF可得出BF=BC-CF=BC-AC,由三角形中位线定理即可得出结论.
证明 (1)如图所示,延长AD交BC于点F,
∵CD平分∠ACB,且AD⊥CD,∴∠CDA=∠CDF=90°,∠ACD=∠FCD.
又∵CD=CD,∴△ACD≌△FCD,∴AC=CF,AD=DF.
∵E是AB的中点,∴DE是△ABF的中位线,∴DE∥BC.
(2)由(1)知DE是△ABF的中位线,AC=CF,
∴DE=BF= (BC-CF)= (BC-AC),即2DE=BC-AC.
点拨
当问题中有中点,且证明线段平行或2倍关系时,我们通常考虑问题能不能应用三角形中位线定理解决.
题型二 构造三角形的中位线解题
例2 如图所示,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,EF分别交BD、AC于点G、H.求证:OG=OH.
分析
取BC边的中点M,连接EM,FM,首先根据三角形的中位线定理得到△EMF是等腰三角形,然后根据等边对等角得到∠MEF=∠MFE,再根据平行线的性质得到∠OGH=∠OHG,最后根据等角对等边即可证得结论.
证明 如图所示,取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,∴MF∥BD,MF=BD,
同理,ME∥AC,ME= AC,
∵AC=BD,∴ME=MF,∴∠MEF=∠MFE.∵MF∥BD,∴∠MFE=∠OGH.
同理,∠MEF=∠OHG,∴∠OGH=∠OHG,∴OG=OH.
点拨
已知三角形一边的中点时,常作辅助线构造出三角形的中位线.
