话说“江苏五年新高考”(徐瑢)新20120908
文档属性
| 名称 | 话说“江苏五年新高考”(徐瑢)新20120908 |

|
|
| 格式 | zip | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-12 00:00:00 | ||
图片预览











文档简介
(共50张PPT)
话说“江苏五年新高考”
一、“五年新高考”内容的分布
1.填空题
(1)新知年年考,难度比较小
五年新增知识点考查一览
新增知识点 2008年 2009年 2010年 2011年 2012年
任意、存在量词
幂函数
零点
算法 √ √ √ √ √
合情、演绎推理 √ √
统计 √ √ √ √ √
概率 √ √ √ √ √
导数 √ √ √ √
复数 √ √ √ √ √
一、“五年新高考”内容的分布
1.填空题
(1)新知年年考,难度比较小
(2)知识要全面,能力不偏废
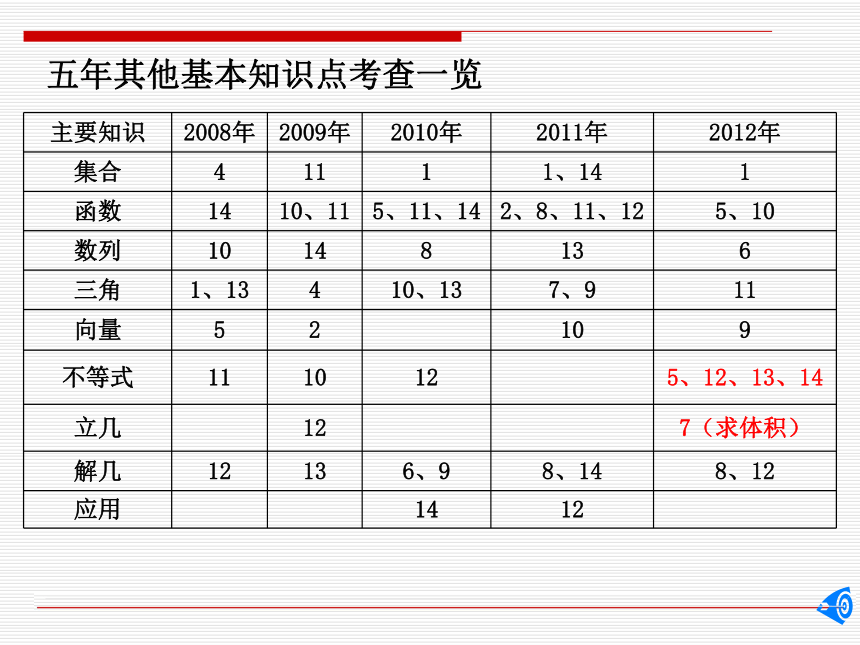
五年其他基本知识点考查一览
主要知识 2008年 2009年 2010年 2011年 2012年
集合 4 11 1 1、14 1
函数 14 10、11 5、11、14 2、8、11、12 5、10
数列 10 14 8 13 6
三角 1、13 4 10、13 7、9 11
向量 5 2 10 9
不等式 11 10 12 5、12、13、14
立几 12 7(求体积)
解几 12 13 6、9 8、14 8、12
应用 14 12
一、“五年新高考”内容的分布
1.填空题
(1)新知年年考,难度比较小
(2)知识要全面,能力不偏废
2.解答题
五年大题一览:
题号 2008年 2009年 2010年 2011年 2012年
15 三角计算 三角向量 向量计算 三角形计算 三角形向量
16 立体几何 立体几何 立几(距离) 立体几何 立体几何
17 应用
(三角、导数) 数列
(整数) 应用
(三角测量) 应用(三次函数、导数) 应用(二次函数,不等式)
18 解几
(抛.圆) 解几
(圆.点) 椭圆
(定点) 椭圆
(恒⊥) 函数综合
19 数列综合 应用
(不等式) 数列综合 函数综合 椭圆
(和定)
20 函数综合 函数综合 函数综合 数列综合 数列综合
二、话说江苏“五年新高考”特点
1. “五年新高考”的命题总特点:
数学命题力求做到“三个避免”:
尽量避免需要死记硬背的内容,
尽量避免呆板题,
尽量避免烦琐计算题.
数学命题还强调“三个反对,两个坚持”:
反对死记硬背,反对题海战术,反对猜题押题;
坚持三基为本,坚持能力为纲.
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(1)填空题的三级跳:50分钟
1——8 ,一望便知,一算即得;
9——12,中等要求,细心不错;
13、14, 小题把关,“事倍功半”.
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(2)解答题的三级跳:70分钟
代数、立几把分送够;
应用、解几区别显著;
函数、数列“几舸”争流.
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(3)附加题:30分钟
21题四中选二,当机立断;
22题中等要求,应对熟练;
23题力求新意,半易半难.
(容易题、中等题、难题之比为5:4:1)
(2009年23题)
(2010年23题)已知△ABC的三边长都是有理数.
(1)求证:cosA是有理数;
(2)对任意正整数n,求证cosnA是有理数.
——有理数
——cos(k+1)A=coskAcosA-sinkAsinA
(2011年23题)
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(4)总体势态:
年份
均分
2008年
2009年
2010年
2011年
2012年
88
把关题有些难
小把关没把关
求变与3误
维稳是大计
立体几何升级
三、“五年新高考”的各年“话题”
1、2008年的话题:
——小题关卡多,题题不省心
——大题要求高,处处难深入
*
考题点击
*
考题点击
*
考题点击
*
三、“五年新高考”的各年“话题”
2、2009年的话题:
——小题把关,一马平川,皆大欢喜!
——首创应用题把关,师生皆言苦不堪!
——压轴题平和常规,背景熟悉易发挥!
14.设{an}是公比为q的等比数列,|q|>1,令bn=an+1(n=1,2,…),若数列{bn}有连续四项在集合{-53,-23,19,37,82}中,则6q= .
【解析】将各数按照绝对值从小到大排列,各数减1,观察即可得解.
考题点击
——这样的填空题怎么把关?
——小题把关,一马平川,皆大欢喜!
考题点击
——首创应用题把关,师生皆言苦不堪!
考题点击
——压轴题平和常规,背景熟悉易发挥!
三、“五年新高考”的各年“话题”
3、2010年的话题:
——填空多题让学生抓狂
——超纲争议令老师纠结
——大题布局受专家称道
——填空多题让学生抓狂
8.函数y=x2(x>0)的图像在点(ak,,ak2)处的切线与x轴交点的横坐标为ak+1,其中k∈N*,若a1=16,则a1+a3+a5的值是 .
——切线斜率是导数,点斜式得切线方程,横截距是数列递推,等比数列,求和;
——6年江苏考了3次,06、10、11三年;
考题点击
(2011年12题)在平面直角坐标系xOy中,已知点P是函数f(x)=ex(x>0)的图象上的动点,该图象在P处的切线l交y轴于点M,过点P作l的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____.
——设点(u,eu),求导,切线方程,求M,
求法线方程,求N,中点纵坐标t=g(u) ,
求函数t=g(u) 的最值
——知识网络交汇处命题,思维运算链长!
考题点击
12.设实数x,y满足3≤ xy2 ≤8,4≤ x2/y ≤9,则x3/y 4的最大值是 .
——构造和化归
解析二:通过取对数,化归为关于lgx和lgy这两个元素的线性规划问题.
考题点击
考题点击
三、“五年新高考”的各年“话题”
4、2011年的话题:
——无可奈何1 3 题,菜鸟开心高手急;
——让人无语应用题,放在中考也不奇;
——压轴大题把住关,寥寥无几能生还!
13.设1≤a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是____.
——a1,a2,a1q,a2+1,a1q2,a2+2,a1q3,…
——找不到切入点,坚持还是放弃?
——无可奈何13题,菜鸟开心高手急!
考题点击
17.请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
——让人无语应用题,放在中考也不奇!
考题点击
20.设M为部分正整数组成的集合,数列{an}的首项a1=1,前n项的和为Sn,已知对任意整数k属于M,
当n>k时,Sn+k+ Sn-k =2(Sn + Sk)都成立.
(1)设M={1},a2=2,求a5的值;
(2)设M={3,4},求数列{an}的通项公式.
——压轴大题把住关,寥寥无几能生还!
考题点击
怎么想?具体写出性质
当k=3时, Sn+3+ Sn-3 =2(Sn + S3),
再写下一个 Sn+4+ Sn-2 =2(Sn+1 + S3),
两个相减得 an+4+ an-2 =2an+1 ,n≥4,
即有 a2,a5,a8,a11,…成等差数列,设公差是3d1;
a3,a6,a9,a12,…成等差数列,设公差是3d2;
a4,a7,a10,a13,…成等差数列,设公差是3d3;
考题点击
——压轴大题把住关,寥寥无几能生还!
当k=4时,同理有 an+5+ an-3 =2an+1 ,n≥5,
即有 a3,a7,a11,a15,…成等差数列,设公差是4b1;
a4,a8,a12,a16,…成等差数列,设公差是4b2;
a5,a9,a13,a17,…成等差数列,设公差是4b3;
a2,a6,a10,a14,…成等差数列,设公差是4b4;
——b1=d2=b2=d3=b3=d1…?
考题点击
——压轴大题把住关,寥寥无几能生还!
18.如图,在平面直角坐标系xOy中,M、N分别是椭圆x2/4+y2/2=1的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
(1)当直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB.
——得分差异最大的试题
O
x
y
C
B
M
P
N
A
考题品味
是巧合还是必然?
点A的轨迹方程是:
有没有更一般性的结论?
*
回归课本,追根溯源
考题品味
o
x
y
B
C
A
(一)纵向探究
回归课本,追根溯源
——归纳得到椭圆的一种“生成方式”
考题品味
(二)逆向探究
回归课本,追根溯源
——得到椭圆的一个性质
考题品味
o
x
y
B
C
A
o
x
y
B
C
A
(三)深度探究
回归课本,追根溯源
——构建椭圆新的认知体系
考题品味
⑴
⑵
⑶
o
x
P
C
A
y
B
N
M
*
回归课本,追根溯源
考题品味
(四)拓展应用
o
x
P
C
A
y
B
N
M
*
回归课本,追根溯源
考题品味
(四)拓展应用
⑶
三、“五年新高考”的各年“话题”
5、2012年的话题:
——立体几何“不甘寂寞”
——应用大题“再惹争议”
——数列问题“皆感意外”
——立体几何“不甘寂寞”
考题点击
17.如图,建立平面直角坐标系 xOy , x 轴在地平面上,y 轴垂直于地平面,单位长度为 1 千米.某炮兵位于坐标原点.已知炮弹发射后的轨迹在方程
表示的曲线上,其中 k 与发射方向有关.炮的射程是炮弹落地点的横坐标.
(1)求跑的最大射程; (2) 设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标 a 不超过多少时,炮弹可以击中它?请说明理由。
——应用大题“再惹争议”
考题点击
——数列问题“皆感意外”
考题点击
四、 思考与启示:
重技能训练向重能力培养转变;
重课后训练向重课堂熏陶转变 ;
重通性通法向重审题分析转变;
重强化运算向重算理算法转变。
谢谢大家!
话说“江苏五年新高考”
一、“五年新高考”内容的分布
1.填空题
(1)新知年年考,难度比较小
五年新增知识点考查一览
新增知识点 2008年 2009年 2010年 2011年 2012年
任意、存在量词
幂函数
零点
算法 √ √ √ √ √
合情、演绎推理 √ √
统计 √ √ √ √ √
概率 √ √ √ √ √
导数 √ √ √ √
复数 √ √ √ √ √
一、“五年新高考”内容的分布
1.填空题
(1)新知年年考,难度比较小
(2)知识要全面,能力不偏废
五年其他基本知识点考查一览
主要知识 2008年 2009年 2010年 2011年 2012年
集合 4 11 1 1、14 1
函数 14 10、11 5、11、14 2、8、11、12 5、10
数列 10 14 8 13 6
三角 1、13 4 10、13 7、9 11
向量 5 2 10 9
不等式 11 10 12 5、12、13、14
立几 12 7(求体积)
解几 12 13 6、9 8、14 8、12
应用 14 12
一、“五年新高考”内容的分布
1.填空题
(1)新知年年考,难度比较小
(2)知识要全面,能力不偏废
2.解答题
五年大题一览:
题号 2008年 2009年 2010年 2011年 2012年
15 三角计算 三角向量 向量计算 三角形计算 三角形向量
16 立体几何 立体几何 立几(距离) 立体几何 立体几何
17 应用
(三角、导数) 数列
(整数) 应用
(三角测量) 应用(三次函数、导数) 应用(二次函数,不等式)
18 解几
(抛.圆) 解几
(圆.点) 椭圆
(定点) 椭圆
(恒⊥) 函数综合
19 数列综合 应用
(不等式) 数列综合 函数综合 椭圆
(和定)
20 函数综合 函数综合 函数综合 数列综合 数列综合
二、话说江苏“五年新高考”特点
1. “五年新高考”的命题总特点:
数学命题力求做到“三个避免”:
尽量避免需要死记硬背的内容,
尽量避免呆板题,
尽量避免烦琐计算题.
数学命题还强调“三个反对,两个坚持”:
反对死记硬背,反对题海战术,反对猜题押题;
坚持三基为本,坚持能力为纲.
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(1)填空题的三级跳:50分钟
1——8 ,一望便知,一算即得;
9——12,中等要求,细心不错;
13、14, 小题把关,“事倍功半”.
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(2)解答题的三级跳:70分钟
代数、立几把分送够;
应用、解几区别显著;
函数、数列“几舸”争流.
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(3)附加题:30分钟
21题四中选二,当机立断;
22题中等要求,应对熟练;
23题力求新意,半易半难.
(容易题、中等题、难题之比为5:4:1)
(2009年23题)
(2010年23题)已知△ABC的三边长都是有理数.
(1)求证:cosA是有理数;
(2)对任意正整数n,求证cosnA是有理数.
——有理数
——cos(k+1)A=coskAcosA-sinkAsinA
(2011年23题)
二、话说江苏“五年新高考”特点
2.“五年新高考”的“坚守”:
(4)总体势态:
年份
均分
2008年
2009年
2010年
2011年
2012年
88
把关题有些难
小把关没把关
求变与3误
维稳是大计
立体几何升级
三、“五年新高考”的各年“话题”
1、2008年的话题:
——小题关卡多,题题不省心
——大题要求高,处处难深入
*
考题点击
*
考题点击
*
考题点击
*
三、“五年新高考”的各年“话题”
2、2009年的话题:
——小题把关,一马平川,皆大欢喜!
——首创应用题把关,师生皆言苦不堪!
——压轴题平和常规,背景熟悉易发挥!
14.设{an}是公比为q的等比数列,|q|>1,令bn=an+1(n=1,2,…),若数列{bn}有连续四项在集合{-53,-23,19,37,82}中,则6q= .
【解析】将各数按照绝对值从小到大排列,各数减1,观察即可得解.
考题点击
——这样的填空题怎么把关?
——小题把关,一马平川,皆大欢喜!
考题点击
——首创应用题把关,师生皆言苦不堪!
考题点击
——压轴题平和常规,背景熟悉易发挥!
三、“五年新高考”的各年“话题”
3、2010年的话题:
——填空多题让学生抓狂
——超纲争议令老师纠结
——大题布局受专家称道
——填空多题让学生抓狂
8.函数y=x2(x>0)的图像在点(ak,,ak2)处的切线与x轴交点的横坐标为ak+1,其中k∈N*,若a1=16,则a1+a3+a5的值是 .
——切线斜率是导数,点斜式得切线方程,横截距是数列递推,等比数列,求和;
——6年江苏考了3次,06、10、11三年;
考题点击
(2011年12题)在平面直角坐标系xOy中,已知点P是函数f(x)=ex(x>0)的图象上的动点,该图象在P处的切线l交y轴于点M,过点P作l的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____.
——设点(u,eu),求导,切线方程,求M,
求法线方程,求N,中点纵坐标t=g(u) ,
求函数t=g(u) 的最值
——知识网络交汇处命题,思维运算链长!
考题点击
12.设实数x,y满足3≤ xy2 ≤8,4≤ x2/y ≤9,则x3/y 4的最大值是 .
——构造和化归
解析二:通过取对数,化归为关于lgx和lgy这两个元素的线性规划问题.
考题点击
考题点击
三、“五年新高考”的各年“话题”
4、2011年的话题:
——无可奈何1 3 题,菜鸟开心高手急;
——让人无语应用题,放在中考也不奇;
——压轴大题把住关,寥寥无几能生还!
13.设1≤a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是____.
——a1,a2,a1q,a2+1,a1q2,a2+2,a1q3,…
——找不到切入点,坚持还是放弃?
——无可奈何13题,菜鸟开心高手急!
考题点击
17.请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包装盒侧面积S(cm)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
——让人无语应用题,放在中考也不奇!
考题点击
20.设M为部分正整数组成的集合,数列{an}的首项a1=1,前n项的和为Sn,已知对任意整数k属于M,
当n>k时,Sn+k+ Sn-k =2(Sn + Sk)都成立.
(1)设M={1},a2=2,求a5的值;
(2)设M={3,4},求数列{an}的通项公式.
——压轴大题把住关,寥寥无几能生还!
考题点击
怎么想?具体写出性质
当k=3时, Sn+3+ Sn-3 =2(Sn + S3),
再写下一个 Sn+4+ Sn-2 =2(Sn+1 + S3),
两个相减得 an+4+ an-2 =2an+1 ,n≥4,
即有 a2,a5,a8,a11,…成等差数列,设公差是3d1;
a3,a6,a9,a12,…成等差数列,设公差是3d2;
a4,a7,a10,a13,…成等差数列,设公差是3d3;
考题点击
——压轴大题把住关,寥寥无几能生还!
当k=4时,同理有 an+5+ an-3 =2an+1 ,n≥5,
即有 a3,a7,a11,a15,…成等差数列,设公差是4b1;
a4,a8,a12,a16,…成等差数列,设公差是4b2;
a5,a9,a13,a17,…成等差数列,设公差是4b3;
a2,a6,a10,a14,…成等差数列,设公差是4b4;
——b1=d2=b2=d3=b3=d1…?
考题点击
——压轴大题把住关,寥寥无几能生还!
18.如图,在平面直角坐标系xOy中,M、N分别是椭圆x2/4+y2/2=1的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
(1)当直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB.
——得分差异最大的试题
O
x
y
C
B
M
P
N
A
考题品味
是巧合还是必然?
点A的轨迹方程是:
有没有更一般性的结论?
*
回归课本,追根溯源
考题品味
o
x
y
B
C
A
(一)纵向探究
回归课本,追根溯源
——归纳得到椭圆的一种“生成方式”
考题品味
(二)逆向探究
回归课本,追根溯源
——得到椭圆的一个性质
考题品味
o
x
y
B
C
A
o
x
y
B
C
A
(三)深度探究
回归课本,追根溯源
——构建椭圆新的认知体系
考题品味
⑴
⑵
⑶
o
x
P
C
A
y
B
N
M
*
回归课本,追根溯源
考题品味
(四)拓展应用
o
x
P
C
A
y
B
N
M
*
回归课本,追根溯源
考题品味
(四)拓展应用
⑶
三、“五年新高考”的各年“话题”
5、2012年的话题:
——立体几何“不甘寂寞”
——应用大题“再惹争议”
——数列问题“皆感意外”
——立体几何“不甘寂寞”
考题点击
17.如图,建立平面直角坐标系 xOy , x 轴在地平面上,y 轴垂直于地平面,单位长度为 1 千米.某炮兵位于坐标原点.已知炮弹发射后的轨迹在方程
表示的曲线上,其中 k 与发射方向有关.炮的射程是炮弹落地点的横坐标.
(1)求跑的最大射程; (2) 设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标 a 不超过多少时,炮弹可以击中它?请说明理由。
——应用大题“再惹争议”
考题点击
——数列问题“皆感意外”
考题点击
四、 思考与启示:
重技能训练向重能力培养转变;
重课后训练向重课堂熏陶转变 ;
重通性通法向重审题分析转变;
重强化运算向重算理算法转变。
谢谢大家!
同课章节目录
