2021--2022学年冀教版八年级数学上册 期中模拟考试试题(word版含答案)
文档属性
| 名称 | 2021--2022学年冀教版八年级数学上册 期中模拟考试试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 137.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 00:00:00 | ||
图片预览


文档简介
2021-2022第一学期八年级期中考试
数学试题(冀教版)
注意事项:1.本试卷共6页,总分120分,考试时间90分钟。
2.答卷前将密封线左侧项目填写清楚。
3.答题用黑色钢笔或黑色碳素笔。
题号 一 二 三 总分
19 20 21 22 23 24 25 26
答案
得分 评卷人
一、选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是符合题目的,把符合题目要求的选项前的字母填写在表格内)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案
1.实数4的算术平方根是 ( )
A.﹣2 B.2 C.±2 D.±4
2.若的值为零,则x的值是 ( )
A.±1 B.1 C.﹣1 D.不存在
3.下列命题是真命题的是 ( )
A.三个角对应相等的两个三角形全等
B.面积相等的两个三角形全等
C.对顶角相等
D.相等的两个角是对顶角
4.下列各式中:①﹣,②,③,④,⑤,⑥,是分式的是 ( )
A.①③④⑥ B.①③⑤ C.①③④⑤ D.③⑤⑥
5.如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定 ( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
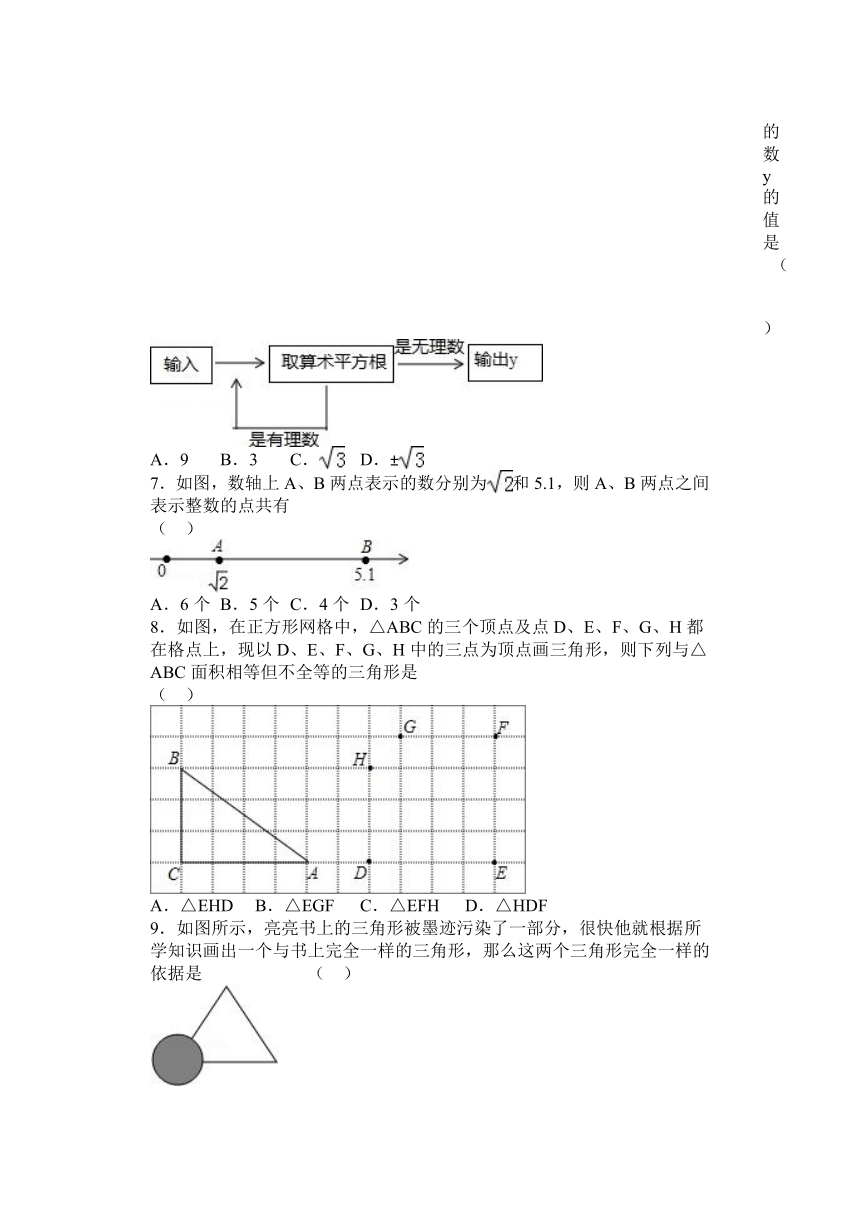
6.有一个数值转换器,程序如图所示,当输入的数x为81时,输出的数y的值是( )
A.9 B.3 C. D.±
7.如图,数轴上A、B两点表示的数分别为和5.1,则A、B两点之间表示整数的点共有 ( )
A.6个 B.5个 C.4个 D.3个
8.如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是 ( )
A.△EHD B.△EGF C.△EFH D.△HDF
9.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( )
A.SSS B.SAS C.AAS D.ASA
10.若关于x的方程=1的解是正数,则a的取值范围是 ( )
A.a>﹣1 B.a>﹣1且a≠0 C.a<﹣1 D.a<﹣1且a≠﹣3
11.已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为 ( )
①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A.③①② B.①②③ C.②③① D.③②①
12.小玲每天骑自行车或步行上学,她上学的路程为2800米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为x米/分,根据题意,下面列出的方程正确的是 ( )
A. B.
C. D.
得分 评卷人
二、填空题(本大题共6个小题,每小题3分,共18分,把答案写在表格内)
13.圆周率π精确到百分位的近似数是
14.已知﹣=3,则分式的值为
15.若两个连续的整数a、b满足a<<b,则的值为
16.分式方程+1=有增根,则m=
17.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
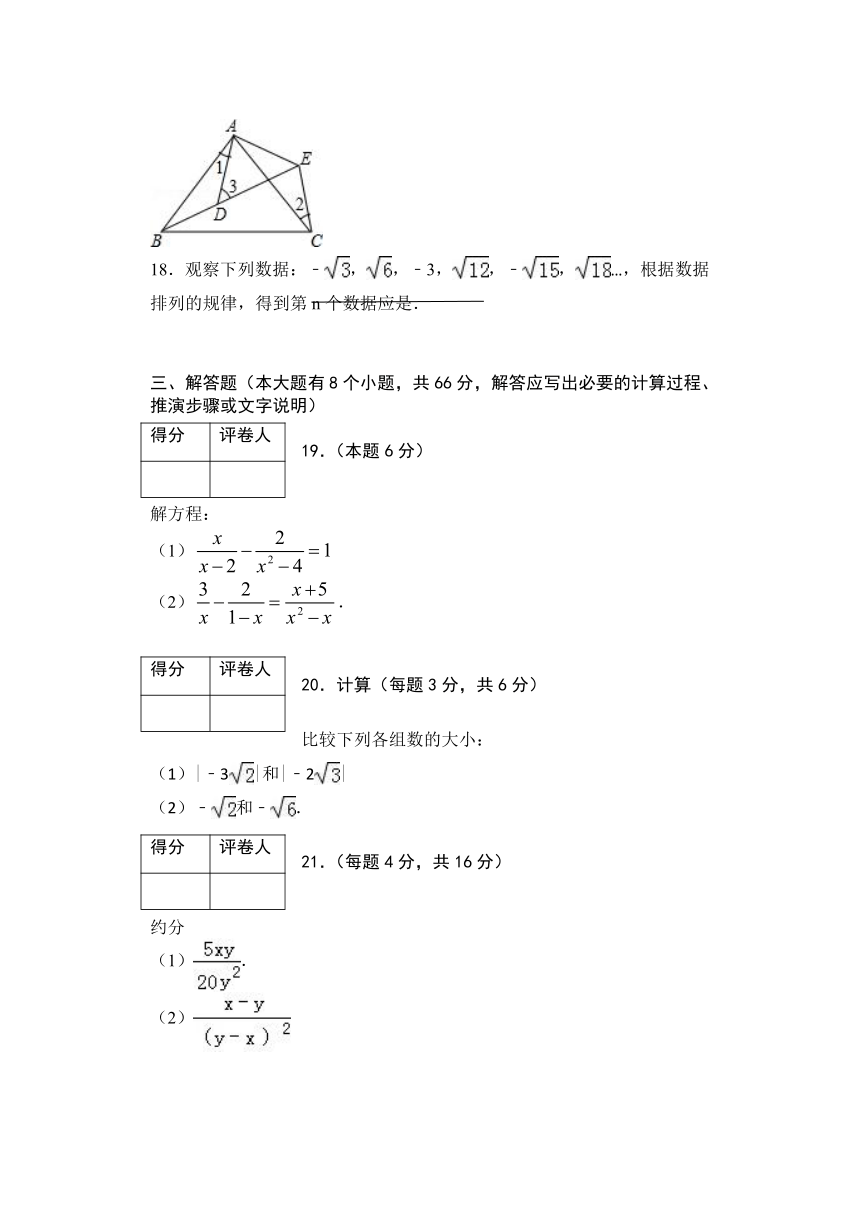
18.观察下列数据:﹣,,﹣3,,﹣,…,根据数据排列的规律,得到第n个数据应是.
三、解答题(本大题有8个小题,共66分,解答应写出必要的计算过程、推演步骤或文字说明)
得分 评卷人
19.(本题6分)
解方程:
(1)
(2).
得分 评卷人
20.计算(每题3分,共6分)
比较下列各组数的大小:
(1)|﹣3|和|﹣2|
(2)﹣和﹣.
得分 评卷人
21.(每题4分,共16分)
约分
(1).
(2)
(3)
(4)通分:,,
得分 评卷人
22.(本题6分)
先化简,再选取一个你喜欢的数代入求值:(+);
得分 评卷人
23.(本题8分)
如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.
得分 评卷人
24.(本题8分)
已知实数a、b满足|a﹣5|+=0
(1)求a,b的值;
(2)求a+b﹣1的立方根.
得分 评卷人
25.(本题8分)
某淘宝商家在2015年6月份用13200元购进了一批牧马人鼠标,后经销售发现供不应求,于是该商家又用28800元购进了第二批这种鼠标,所购数量是第一批购进量的2倍,但每个鼠标的单价贵了10元.
(1)求该商家第一次购进的鼠标的数量;
(2)若两批鼠标按相同的售价进行出售,最后剩下的50个鼠标按售价的八折出售,如果两批鼠标全部售完后,总利润恰好为两次总进价的25%,求每个鼠标的售价.
得分 评卷人
26.(本题8分)
如图,在△ABC中,AD,CE是高,AD与CE交于点F,连接BF,延长AD到点G,使得AG=BC,连接BG,若CF=AB.
(1)试判断BF与BG之间的数量关系,并说明理由;
(2)求∠FBG的度数.
参考答案
1-6B C C B B C 6-12 C D D D A A
13.3.
14..
15. .
16.3
17. 55°.
18. (﹣1)n.
19. 解:(1)去分母得:x2+2x﹣2=x2﹣4,
解得:x=﹣1,
经检验x=﹣1是分式方程的解;
(2)去分母得:3x﹣3+2x=x+5,
解得:x=2,
经检验x=2是增根,分式方程无解.
20. 1)∵,
∵|﹣3|>|﹣2|,
(2)∵,
∴.
21. 解:(1)原式==,
(2)原式==,
(3)原式==,
(4)最简公分母10a2b2c2,
=,
=,
=﹣;
22.原式=(+) = =,
当x=2时,原式=2;
23.解:∵C是AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B,∠DCE=∠E,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS),
∴AD=CE,∠D=∠E,
∴∠DCE=∠D,
∴AD∥CE,
所以AD与CE平行且相等.
24.解:(1)∵|a﹣5|+=0,
a﹣5=0,b2﹣16=0,
解得a=5,b=±4;
(2)当a=5,b=4时,a+b﹣1=5+4﹣1=8,∴=2;
当a=5,b=﹣4时,a+b﹣1=5﹣4﹣1=0,∴=0.
25.解:(1)设该商家购进的第一批衬衫是x件,则购进第二批这种衬衫是2x件,依题意有
+10=,
解得x=120,
经检验,x=120是原方程的解,且符合题意.
答:该商家购进的第一批鼠标是120个.
(2)3x=3×120=360,
设每件鼠标的标价y元,依题意有
(360﹣50)y+50×0.8y≥(13200+28800)×(1+25%),
解得y≥150.
答:每件鼠标的标价至少是150元.
26.解:(1)BF=BG;
∵AD,CE是高,
∴∠BAD+∠AFE=∠BCF+∠CFD=90°,
∵∠AFE=∠CFD,
∴∠BAD=∠BCF,
在△ABG与△CFB中,
,
∴△ABG≌△CFB,
∴BF=BG;
(2)∵△ABG≌△CFB,
∴∠G=∠FBD,
∵∠FBD+∠DBG=90°,
∴∠G+∠DBG=90°,
∴∠FBG的度数为90°.
数学试题(冀教版)
注意事项:1.本试卷共6页,总分120分,考试时间90分钟。
2.答卷前将密封线左侧项目填写清楚。
3.答题用黑色钢笔或黑色碳素笔。
题号 一 二 三 总分
19 20 21 22 23 24 25 26
答案
得分 评卷人
一、选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是符合题目的,把符合题目要求的选项前的字母填写在表格内)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
答案
1.实数4的算术平方根是 ( )
A.﹣2 B.2 C.±2 D.±4
2.若的值为零,则x的值是 ( )
A.±1 B.1 C.﹣1 D.不存在
3.下列命题是真命题的是 ( )
A.三个角对应相等的两个三角形全等
B.面积相等的两个三角形全等
C.对顶角相等
D.相等的两个角是对顶角
4.下列各式中:①﹣,②,③,④,⑤,⑥,是分式的是 ( )
A.①③④⑥ B.①③⑤ C.①③④⑤ D.③⑤⑥
5.如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定 ( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
6.有一个数值转换器,程序如图所示,当输入的数x为81时,输出的数y的值是( )
A.9 B.3 C. D.±
7.如图,数轴上A、B两点表示的数分别为和5.1,则A、B两点之间表示整数的点共有 ( )
A.6个 B.5个 C.4个 D.3个
8.如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是 ( )
A.△EHD B.△EGF C.△EFH D.△HDF
9.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( )
A.SSS B.SAS C.AAS D.ASA
10.若关于x的方程=1的解是正数,则a的取值范围是 ( )
A.a>﹣1 B.a>﹣1且a≠0 C.a<﹣1 D.a<﹣1且a≠﹣3
11.已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为 ( )
①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A.③①② B.①②③ C.②③① D.③②①
12.小玲每天骑自行车或步行上学,她上学的路程为2800米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为x米/分,根据题意,下面列出的方程正确的是 ( )
A. B.
C. D.
得分 评卷人
二、填空题(本大题共6个小题,每小题3分,共18分,把答案写在表格内)
13.圆周率π精确到百分位的近似数是
14.已知﹣=3,则分式的值为
15.若两个连续的整数a、b满足a<<b,则的值为
16.分式方程+1=有增根,则m=
17.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
18.观察下列数据:﹣,,﹣3,,﹣,…,根据数据排列的规律,得到第n个数据应是.
三、解答题(本大题有8个小题,共66分,解答应写出必要的计算过程、推演步骤或文字说明)
得分 评卷人
19.(本题6分)
解方程:
(1)
(2).
得分 评卷人
20.计算(每题3分,共6分)
比较下列各组数的大小:
(1)|﹣3|和|﹣2|
(2)﹣和﹣.
得分 评卷人
21.(每题4分,共16分)
约分
(1).
(2)
(3)
(4)通分:,,
得分 评卷人
22.(本题6分)
先化简,再选取一个你喜欢的数代入求值:(+);
得分 评卷人
23.(本题8分)
如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.
得分 评卷人
24.(本题8分)
已知实数a、b满足|a﹣5|+=0
(1)求a,b的值;
(2)求a+b﹣1的立方根.
得分 评卷人
25.(本题8分)
某淘宝商家在2015年6月份用13200元购进了一批牧马人鼠标,后经销售发现供不应求,于是该商家又用28800元购进了第二批这种鼠标,所购数量是第一批购进量的2倍,但每个鼠标的单价贵了10元.
(1)求该商家第一次购进的鼠标的数量;
(2)若两批鼠标按相同的售价进行出售,最后剩下的50个鼠标按售价的八折出售,如果两批鼠标全部售完后,总利润恰好为两次总进价的25%,求每个鼠标的售价.
得分 评卷人
26.(本题8分)
如图,在△ABC中,AD,CE是高,AD与CE交于点F,连接BF,延长AD到点G,使得AG=BC,连接BG,若CF=AB.
(1)试判断BF与BG之间的数量关系,并说明理由;
(2)求∠FBG的度数.
参考答案
1-6B C C B B C 6-12 C D D D A A
13.3.
14..
15. .
16.3
17. 55°.
18. (﹣1)n.
19. 解:(1)去分母得:x2+2x﹣2=x2﹣4,
解得:x=﹣1,
经检验x=﹣1是分式方程的解;
(2)去分母得:3x﹣3+2x=x+5,
解得:x=2,
经检验x=2是增根,分式方程无解.
20. 1)∵,
∵|﹣3|>|﹣2|,
(2)∵,
∴.
21. 解:(1)原式==,
(2)原式==,
(3)原式==,
(4)最简公分母10a2b2c2,
=,
=,
=﹣;
22.原式=(+) = =,
当x=2时,原式=2;
23.解:∵C是AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B,∠DCE=∠E,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS),
∴AD=CE,∠D=∠E,
∴∠DCE=∠D,
∴AD∥CE,
所以AD与CE平行且相等.
24.解:(1)∵|a﹣5|+=0,
a﹣5=0,b2﹣16=0,
解得a=5,b=±4;
(2)当a=5,b=4时,a+b﹣1=5+4﹣1=8,∴=2;
当a=5,b=﹣4时,a+b﹣1=5﹣4﹣1=0,∴=0.
25.解:(1)设该商家购进的第一批衬衫是x件,则购进第二批这种衬衫是2x件,依题意有
+10=,
解得x=120,
经检验,x=120是原方程的解,且符合题意.
答:该商家购进的第一批鼠标是120个.
(2)3x=3×120=360,
设每件鼠标的标价y元,依题意有
(360﹣50)y+50×0.8y≥(13200+28800)×(1+25%),
解得y≥150.
答:每件鼠标的标价至少是150元.
26.解:(1)BF=BG;
∵AD,CE是高,
∴∠BAD+∠AFE=∠BCF+∠CFD=90°,
∵∠AFE=∠CFD,
∴∠BAD=∠BCF,
在△ABG与△CFB中,
,
∴△ABG≌△CFB,
∴BF=BG;
(2)∵△ABG≌△CFB,
∴∠G=∠FBD,
∵∠FBD+∠DBG=90°,
∴∠G+∠DBG=90°,
∴∠FBG的度数为90°.
同课章节目录
