贵州册亨二中2012-2013学年高二上学期8月月考数学(理)试题
文档属性
| 名称 | 贵州册亨二中2012-2013学年高二上学期8月月考数学(理)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 186.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-13 00:00:00 | ||
图片预览




文档简介
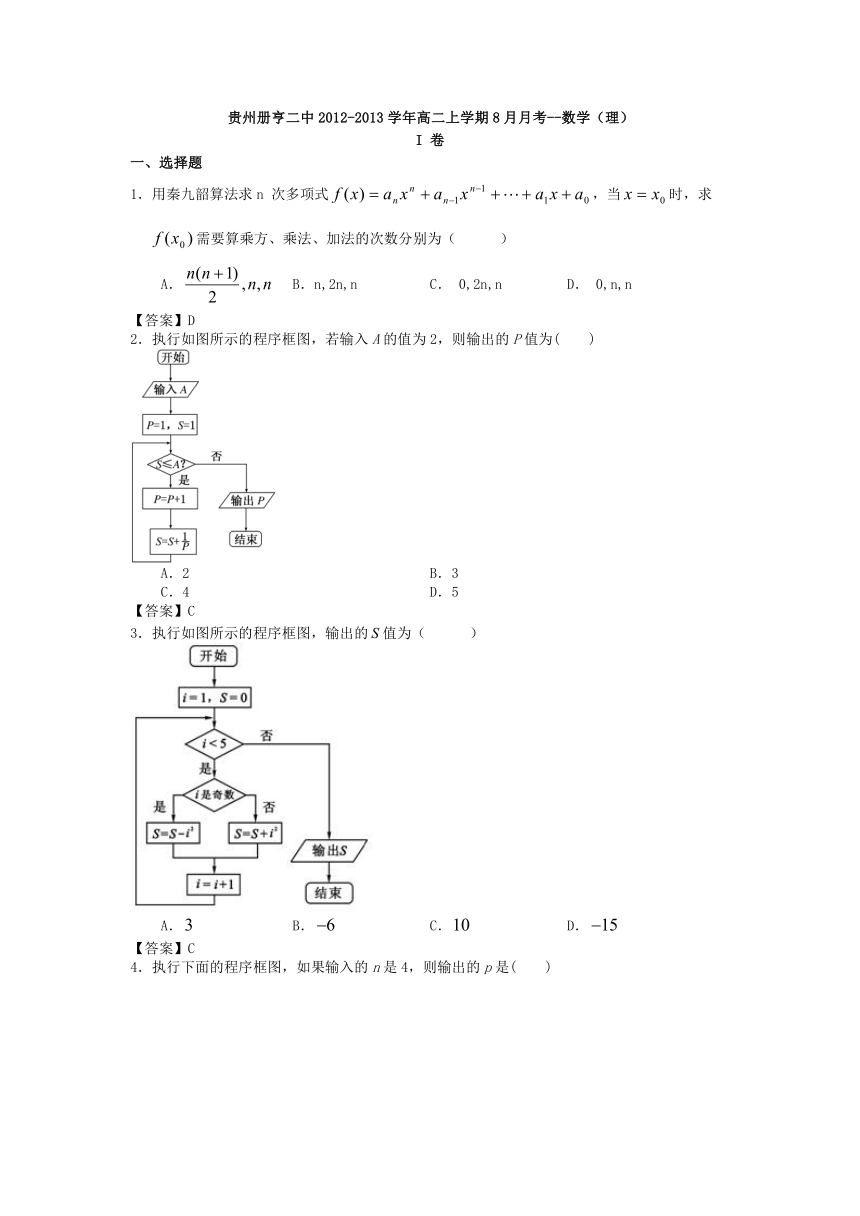
贵州册亨二中2012-2013学年高二上学期8月月考--数学(理)
I 卷
一、选择题
1.用秦九韶算法求n 次多项式,当时,求需要算乘方、乘法、加法的次数分别为( )
A. B.n,2n,n C. 0,2n,n D. 0,n,n
【答案】D
2.执行如图所示的程序框图,若输入A的值为2,则输出的P值为( )
A.2 B.3
C.4 D.5
【答案】C
3.执行如图所示的程序框图,输出的值为( )
A. B. C. D.
【答案】C
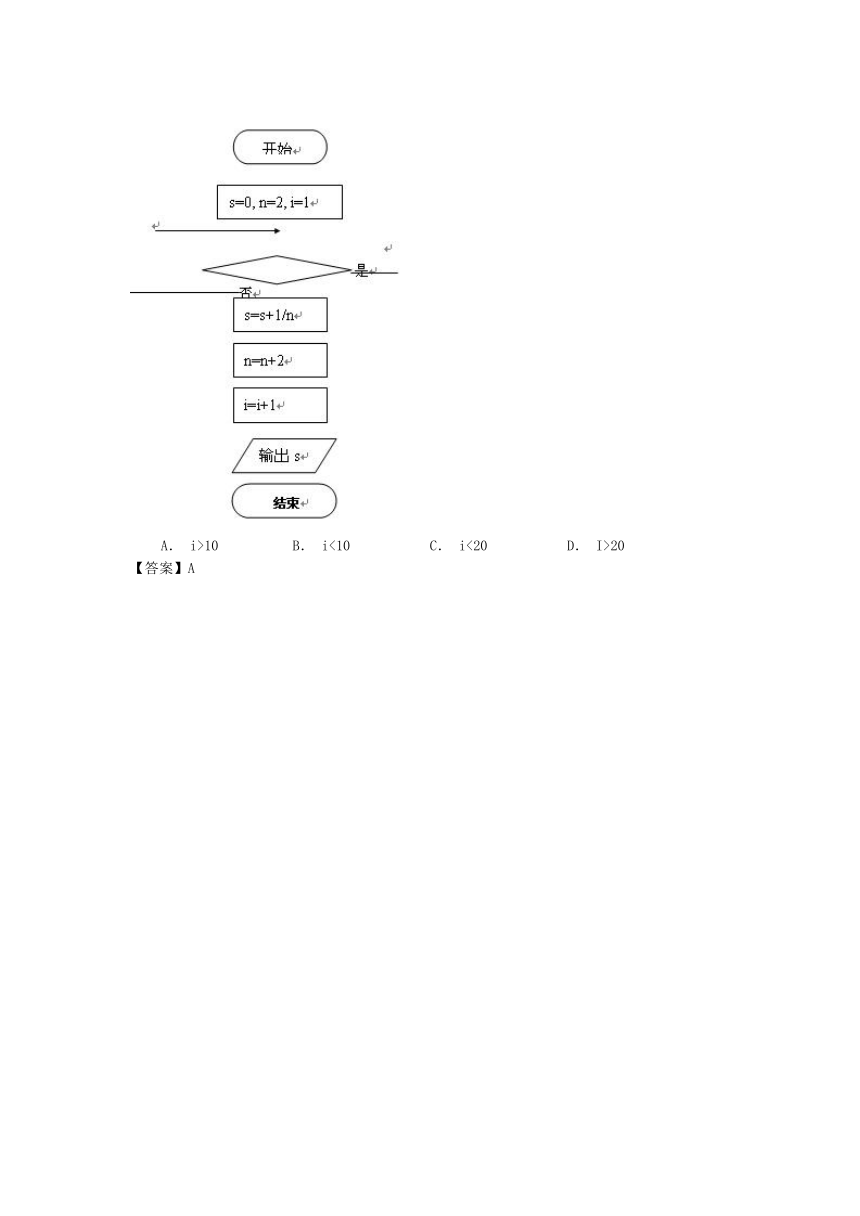
4.执行下面的程序框图,如果输入的n是4,则输出的p是( )
A.8 B.5
C.3 D.2
【答案】C
5.下列给出的赋值语句中正确的是( )
A.3=A B. M=-M C. B=A=2 D.
【答案】B
6.执行下面的程序框图,如果输入的N是6,那么输出的p是( )
A.120 B.720
C.1440 D.5040
【答案】B
7.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法( )
A.S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播
B.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播
C.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播
D.吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶
【答案】C
8.把十进制数15化为二进制数为( C )
A. 1011 B.1001 (2) C. 1111(2) D.1111
【答案】C
9.如图所示的算法流程图中(注:“”也可写成“”或“”, 均表示赋值语句),第3个输出的数是( )
A.1 B.
C. D.
【答案】C
10.以下关于排序的说法中,正确的是( )
A.排序就是将数按从小到大的顺序排序
B.排序只有两种方法,即直接插入排序和冒泡排序
C.用冒泡排序把一列数从小到大排序时,最小的数逐趟向上漂浮
D.用冒泡排序把一列数从小到大排序时,最大的数逐趟向上漂浮
【答案】C
11.计算机执行下面的程序段后,输出的结果是( )
A. B. C. D.
【答案】B
12.以下给出的是计算的值的一个程序框图(如图所示),其中判断框内应填入的条件是( )
A. i>10 B. i<10 C. i<20 D. I>20
【答案】A
II卷
二、填空题
13.如图,是一程序框图,则输出结果为________.
【答案】
14.用更相减损术求38与23的最大公约数为
【答案】1
15.下列给出的几个式子中,正确的赋值语句是(填序号)
①3←A ; ②M← —M ; ③B←A←2 ; ④x+y←0
【答案】②
16. 用秦九韶算法计算多项式当时的值时,至多需要做乘法和加法的次数分别是 _和
【答案】6 , 6
三、解答题
17.请.从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.
【答案】
18.将下列问题的算法改用 “Do…End Do”语句表示,并画出其流程图。
【答案】
19. 写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
【答案】
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
20. 我国《算经十书》之一《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?答曰:二十三.”你
能用程序解决这个问题吗?
【答案】设物共m个,被3,5,7除所得的商分别为x、y、z,则这个问题相当于求不定方程
的正整数解.
m应同时满足下列三个条件:(1)m MOD 3=2;(2)m MOD 5=3;
(3)m MOD 7=2.因此,可以让m从2开始检验,若3个条件中有任何一个不成立,则m递增1,一直到m同时满足三个条件为止.
程序:m=2
f=0
WHILE f=0
IF m MOD 3=2 AND m MOD 5=3
AND m MOD 7=2 THEN
PRINT “物体的个数为:”;m
f=1
ELSE
m=m+1
END IF
WEND
END
21. 我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一凡百钱,买鸡百只,问鸡翁、母、雏各几何?”你能用程序解决这个问题吗?
【答案】设鸡翁、母、雏各x、y、z只,则
由②,得z=100-x-y, ③
③代入①,得5x+3y+=100,
7x+4y=100. ④
求方程④的解,可由程序解之.
程序:x=1
y=1
WHILE x<=14
WHILE y<=25
IF 7*x+4*y=100 THEN
z=100-x-y
PRINT “鸡翁、母、雏的个数别为:”;x,y,z
END IF
y=y+1
WEND
x=x+1
y=1
WEND
END
(法二)实际上,该题可以不对方程组进行化简,通过设置多重循环的方式得以实现.由①、②可得x最大值为20,y最大值为33,z最大值为100,且z为3的倍数.程序如下:
x=1
y=1
z=3
WHILE x<=20
WHILE y<=33
WHILE z<=100
IF 5*x+3*y+z3=100 AND
x+y+z=100 THEN
PRINT “鸡翁、母、雏的个数分别为:”;x、y、z
END IF
z=z+3
WEND
y=y+1
z=3
WEND
x=x+1
y=1
WEND
END
22.设计程序框图求的值.
【答案】程序框图如图所示:
I 卷
一、选择题
1.用秦九韶算法求n 次多项式,当时,求需要算乘方、乘法、加法的次数分别为( )
A. B.n,2n,n C. 0,2n,n D. 0,n,n
【答案】D
2.执行如图所示的程序框图,若输入A的值为2,则输出的P值为( )
A.2 B.3
C.4 D.5
【答案】C
3.执行如图所示的程序框图,输出的值为( )
A. B. C. D.
【答案】C
4.执行下面的程序框图,如果输入的n是4,则输出的p是( )
A.8 B.5
C.3 D.2
【答案】C
5.下列给出的赋值语句中正确的是( )
A.3=A B. M=-M C. B=A=2 D.
【答案】B
6.执行下面的程序框图,如果输入的N是6,那么输出的p是( )
A.120 B.720
C.1440 D.5040
【答案】B
7.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法( )
A.S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播
B.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播
C.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播
D.吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶
【答案】C
8.把十进制数15化为二进制数为( C )
A. 1011 B.1001 (2) C. 1111(2) D.1111
【答案】C
9.如图所示的算法流程图中(注:“”也可写成“”或“”, 均表示赋值语句),第3个输出的数是( )
A.1 B.
C. D.
【答案】C
10.以下关于排序的说法中,正确的是( )
A.排序就是将数按从小到大的顺序排序
B.排序只有两种方法,即直接插入排序和冒泡排序
C.用冒泡排序把一列数从小到大排序时,最小的数逐趟向上漂浮
D.用冒泡排序把一列数从小到大排序时,最大的数逐趟向上漂浮
【答案】C
11.计算机执行下面的程序段后,输出的结果是( )
A. B. C. D.
【答案】B
12.以下给出的是计算的值的一个程序框图(如图所示),其中判断框内应填入的条件是( )
A. i>10 B. i<10 C. i<20 D. I>20
【答案】A
II卷
二、填空题
13.如图,是一程序框图,则输出结果为________.
【答案】
14.用更相减损术求38与23的最大公约数为
【答案】1
15.下列给出的几个式子中,正确的赋值语句是(填序号)
①3←A ; ②M← —M ; ③B←A←2 ; ④x+y←0
【答案】②
16. 用秦九韶算法计算多项式当时的值时,至多需要做乘法和加法的次数分别是 _和
【答案】6 , 6
三、解答题
17.请.从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.
【答案】
18.将下列问题的算法改用 “Do…End Do”语句表示,并画出其流程图。
【答案】
19. 写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
【答案】
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
20. 我国《算经十书》之一《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?答曰:二十三.”你
能用程序解决这个问题吗?
【答案】设物共m个,被3,5,7除所得的商分别为x、y、z,则这个问题相当于求不定方程
的正整数解.
m应同时满足下列三个条件:(1)m MOD 3=2;(2)m MOD 5=3;
(3)m MOD 7=2.因此,可以让m从2开始检验,若3个条件中有任何一个不成立,则m递增1,一直到m同时满足三个条件为止.
程序:m=2
f=0
WHILE f=0
IF m MOD 3=2 AND m MOD 5=3
AND m MOD 7=2 THEN
PRINT “物体的个数为:”;m
f=1
ELSE
m=m+1
END IF
WEND
END
21. 我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一凡百钱,买鸡百只,问鸡翁、母、雏各几何?”你能用程序解决这个问题吗?
【答案】设鸡翁、母、雏各x、y、z只,则
由②,得z=100-x-y, ③
③代入①,得5x+3y+=100,
7x+4y=100. ④
求方程④的解,可由程序解之.
程序:x=1
y=1
WHILE x<=14
WHILE y<=25
IF 7*x+4*y=100 THEN
z=100-x-y
PRINT “鸡翁、母、雏的个数别为:”;x,y,z
END IF
y=y+1
WEND
x=x+1
y=1
WEND
END
(法二)实际上,该题可以不对方程组进行化简,通过设置多重循环的方式得以实现.由①、②可得x最大值为20,y最大值为33,z最大值为100,且z为3的倍数.程序如下:
x=1
y=1
z=3
WHILE x<=20
WHILE y<=33
WHILE z<=100
IF 5*x+3*y+z3=100 AND
x+y+z=100 THEN
PRINT “鸡翁、母、雏的个数分别为:”;x、y、z
END IF
z=z+3
WEND
y=y+1
z=3
WEND
x=x+1
y=1
WEND
END
22.设计程序框图求的值.
【答案】程序框图如图所示:
同课章节目录
