14.2乘法公式 达标训练题--2021--2022学年人教版(2012)八年级上册数学(word版含答案)
文档属性
| 名称 | 14.2乘法公式 达标训练题--2021--2022学年人教版(2012)八年级上册数学(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 327.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 10:04:14 | ||
图片预览




文档简介
14.2乘法公式达标训练题--2021--2022学年人教版(2012)八年级上学期第十四章整式的乘法与因式分解
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列运算正确的是( )
A.(x+y)(﹣y+x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(y﹣x)=x2﹣y2
2.已知,xy=3,则等于( )
A.25 B.-25 C.19 D.-19
3.如图,在边长为的正方形中剪去一个边长为的小正方形,把剩下的部分拼成一个梯形,分别计算这两个阴影部分的面积,这个过程验证了公式( )
A. B.
C. D.
4.已知,则的值是( )
A. B. C. D.
5.下列各式能用平方差公式计算的是( )
A.(2a+b)(2b﹣a) B.(﹣x+1)(﹣x﹣1)
C.(a+b)(a﹣2b) D.(2x﹣1)(﹣2x+1)
6.若x+y=6,x2+y2=20,求x-y的值是( )
A.2 B.﹣2 C.4 D.±2
7.已知,x2+kx+9是一个完全平方式,则k的值是( )
A.-6 B.3 C.6 D.±6
8.已知,则的值( )
A.10 B.6 C.5 D.3
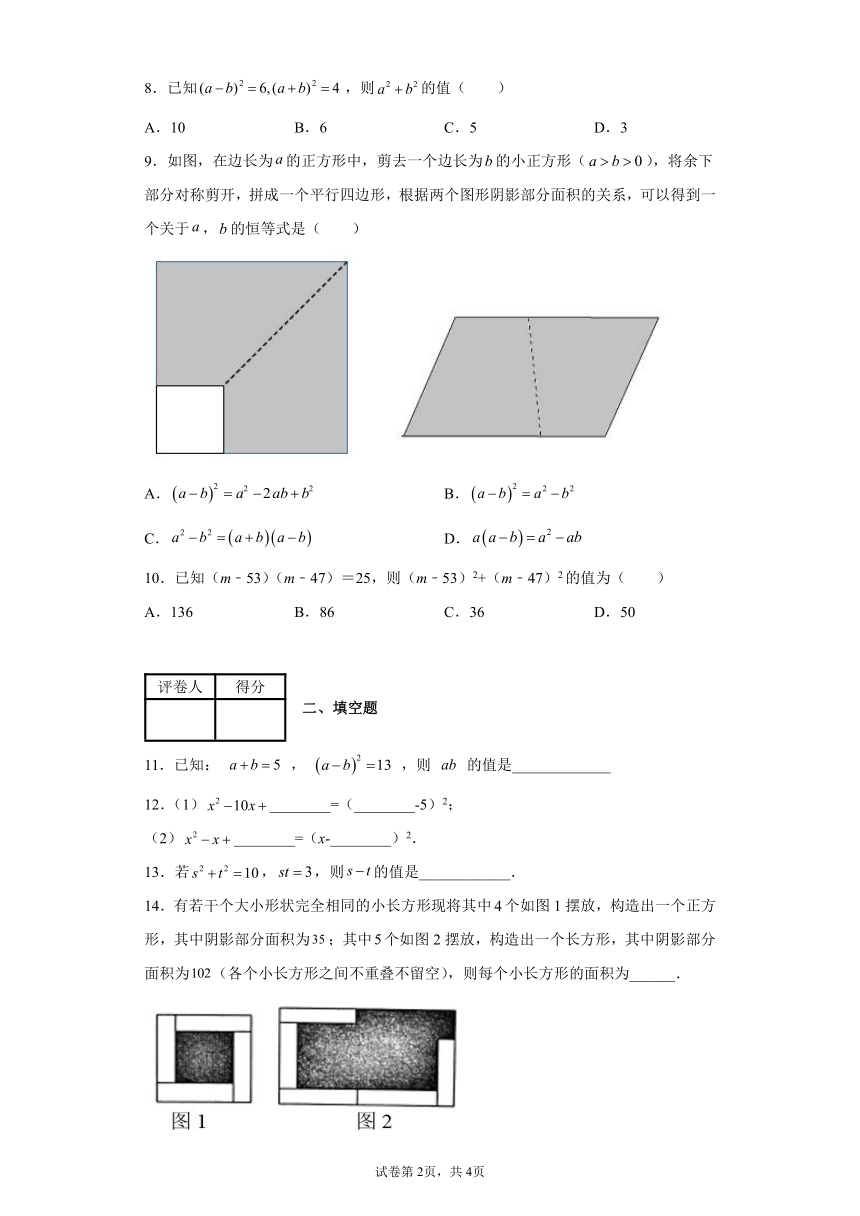
9.如图,在边长为的正方形中,剪去一个边长为的小正方形(),将余下部分对称剪开,拼成一个平行四边形,根据两个图形阴影部分面积的关系,可以得到一个关于,的恒等式是( )
A. B.
C. D.
10.已知(m﹣53)(m﹣47)=25,则(m﹣53)2+(m﹣47)2的值为( )
A.136 B.86 C.36 D.50
评卷人得分
二、填空题
11.已知: , ,则 的值是_____________
12.(1)________=(________-5)2;
(2)________=(x-________)2.
13.若,,则的值是____________.
14.有若干个大小形状完全相同的小长方形现将其中个如图1摆放,构造出一个正方形,其中阴影部分面积为;其中个如图2摆放,构造出一个长方形,其中阴影部分面积为(各个小长方形之间不重叠不留空),则每个小长方形的面积为______.
评卷人得分
三、解答题
15.计算:
(1);
(2).
16.已知A=,B=,
(1)求;
(2)嘉琪认为随着x取不同的数,的值可以是正数,零,负数,你同意他的说法么?并说明理由.
17.用乘法公式简算
(1)199×201;
(2)20132﹣2014×2012.
18.数学活动课上,张老师准备了若干个如图①的三种纸片,种纸片是边长为的正方形,种纸片是边长为的正方形,种纸片是长为,宽为的长方形,并用种纸片一张,种纸片一张,种纸片两张拼成如图②的大正方形.
(1)仔细观察图①、图②,请你写出代数式,,之间的等量关系是____.
(2)根据(1)中的等量关系,解决下列问题:
①已知,,求的值;
②已知,求的值.
19.阅读材料:若m2-2mn+2n2-8n+16=0,求m,n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,(m-n)2+(n-4)2=0,
∴(m-n)2=0,(n-4)2=0,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知△ABC的三边长a,b,c,且满足a2+b2-10a-12b+61=0,求c的取值范围;
(2)已知P=2x2+4y+13,Q=x2-y2+6x-1,比较P,Q的大小.
20.去年,某校为提升学生综合素质,推出了一系列校本课程,“蔬菜种植课”上,张老师用两条宽均为y米的小道将一块长(3x+y)米,宽(3x-y)米的长方形分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分(如图①的形状).
(1)求图①中两条小道的面积之和并化简;
(2)由于去年学生报名人数有限,张老师只要求学生们在Ⅰ部分土地上种植A型蔬菜,在Ⅱ部分土地上种植B型蔬菜,已知种植A型蔬菜每平方米的产量是6千克,种植B型蔬菜每平方米的产量是4千克,求去年种植蔬菜的总产量并化简;
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【详解】
A. (x+y)(﹣y+x)=x2﹣y2,故该选项正确,符合题意;
B. (﹣x+y)2=x2-2xy+y2,故该选项不正确,不符合题意;
C. (﹣x﹣y)2=x2+2xy+y2,故该选项不正确,不符合题意;
D. (x+y)(y﹣x)=y2﹣x2,故该选项不正确,不符合题意;
故选A
2.C
【详解】
解:∵,xy=3,
∴=(x+y)2 2xy=52 2×3=25 6=19,
故选:C.
3.A
【详解】:∵左图中阴影部分的面积是a2 b2,右图中梯形的面积是
(2a+2b)(a b)=(a+b)(a b),
∴a2 b2=(a+b)(a b).
故选:A.
4.B
解:由两边同时平方得:
,
∴;
故选:B.
5.B
解:、不存在互为相同和相反的项,不能用平方差公式计算,故本选项不符合题意;
B、是相同的项,互为相反项是与,符合平方差公式的要求,故本选项符合题意;
C、a是相同的项,不存在相反的项,不能用平方差公式计算,故本选项错误 ;
D、 中符合完全平方公式,不能用平方差公式计算,故本选项错误.
故选B.
6.D
解:∵x+y=6,x2+y2=(x+y)2 2xy=20,
∴2xy=62 20=16,
∴xy=8,
∴(x y)2=x2+y2 2xy=20 2×8=4,
∴x y=±2,
故选:D.
7.D
解:∵x的二次三项式x2+kx+9可以写成一个完全平方式,
∴x2+kx+9=(x±3)2=x2±6x+9,
∴k=±6.
故选:D.
8.C
解:∵(a-b)2=6,
∴a2-2ab+b2=6①
∵(a+b)2=4,
∴a2+2ab+b2=4②
①+②得,2a2+2b2=10,
∴a2+b2=5
故选:C.
9.A
解:根据正方形的图形可知,阴影部分的面积为,
平行四边形的底边长为,高为,
故平行四边形的面积为,
由此可以得到一个关于,的恒等式是,
故选:C.
10.B
解:设a=m-53,b=m-47,则ab=25,a-b=-6,
∴a2+b2=(a-b)2+2ab=(-6)2+50=86,
∴(m-53)2+(m-47)2=86,
故选:B.
11.3
解:∵,
∴,即 ①,
∵,
∴②,
由①-②,得: ,
解得:.
故答案为:3.
12.25
解:(1),即:,
(2),即:,
故答案为:(1)25;;(2);.
13.±2
解:∵(s-t)2=s2-2st+t2=10-6=4,
∴s-t=±2,
故答案为:±2.
14.8
解:设长方形的长为a,宽为b,
由图1可得, 4ab=35,
即=2ab+35①,
由图2可得,(2a+b)(a+2b) 5ab=102,
即=51②,
由①②得,2ab+35=51,
所以ab=8,
即长方形的面积为8,
故答案为:8.
15.(1);(2).
解:(1)
(2)
16.(1)=;(2)不同意,理由见详解.
解:(1),
=,
=;
(2)不同意,理由如下
=,
∵,
∴,
∴随着x取不同的数,的值总是正数.
∴嘉琪的说法不正确,不同意他的说法.
17.(1)39999;(2)1
(1)原式=(200-1)×(200+1)
=2002-12
=40000-1
=39999;
(2)20132﹣(2013+1)×(2013-1)
=20132-20132+1
=1.
18.(1);(2)①3,②
解:(1).
(2)①,
.
.
,
.
②设,则,.
,
.
.
.
.
即.
.
19.(1)1<c<11;(2)P>Q.
解:(1)∵a2+b2-10a-12b+61=0,
∴a2-10a+25+b2-12b+36=0,
∴(a-5)2+(b-6)2=0,
∵(a-5)2≥0,(b-6)2≥0,
∴a-5=0,b-6=0,
解得:a=5,b=6,
∵a,b,c,是△ABC的三边长,
∴6-5<c<6+5,
即:1<c<11;
(2)由题知P-Q=2x2+4y+13-(x2-y2+6x-1)
=x2-6x+9+y2+4y+4+1
=(x-3)2+(y+2)2+1>0,
∴P>Q.
20.(1)图①中两条小道的面积之和为米2;(2)去年种植蔬菜的总产量为.
解:(1)两条小道的面积之和:
;
∴两条小道的面积之和为米2;
(2)根据题意,
.
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列运算正确的是( )
A.(x+y)(﹣y+x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(y﹣x)=x2﹣y2
2.已知,xy=3,则等于( )
A.25 B.-25 C.19 D.-19
3.如图,在边长为的正方形中剪去一个边长为的小正方形,把剩下的部分拼成一个梯形,分别计算这两个阴影部分的面积,这个过程验证了公式( )
A. B.
C. D.
4.已知,则的值是( )
A. B. C. D.
5.下列各式能用平方差公式计算的是( )
A.(2a+b)(2b﹣a) B.(﹣x+1)(﹣x﹣1)
C.(a+b)(a﹣2b) D.(2x﹣1)(﹣2x+1)
6.若x+y=6,x2+y2=20,求x-y的值是( )
A.2 B.﹣2 C.4 D.±2
7.已知,x2+kx+9是一个完全平方式,则k的值是( )
A.-6 B.3 C.6 D.±6
8.已知,则的值( )
A.10 B.6 C.5 D.3
9.如图,在边长为的正方形中,剪去一个边长为的小正方形(),将余下部分对称剪开,拼成一个平行四边形,根据两个图形阴影部分面积的关系,可以得到一个关于,的恒等式是( )
A. B.
C. D.
10.已知(m﹣53)(m﹣47)=25,则(m﹣53)2+(m﹣47)2的值为( )
A.136 B.86 C.36 D.50
评卷人得分
二、填空题
11.已知: , ,则 的值是_____________
12.(1)________=(________-5)2;
(2)________=(x-________)2.
13.若,,则的值是____________.
14.有若干个大小形状完全相同的小长方形现将其中个如图1摆放,构造出一个正方形,其中阴影部分面积为;其中个如图2摆放,构造出一个长方形,其中阴影部分面积为(各个小长方形之间不重叠不留空),则每个小长方形的面积为______.
评卷人得分
三、解答题
15.计算:
(1);
(2).
16.已知A=,B=,
(1)求;
(2)嘉琪认为随着x取不同的数,的值可以是正数,零,负数,你同意他的说法么?并说明理由.
17.用乘法公式简算
(1)199×201;
(2)20132﹣2014×2012.
18.数学活动课上,张老师准备了若干个如图①的三种纸片,种纸片是边长为的正方形,种纸片是边长为的正方形,种纸片是长为,宽为的长方形,并用种纸片一张,种纸片一张,种纸片两张拼成如图②的大正方形.
(1)仔细观察图①、图②,请你写出代数式,,之间的等量关系是____.
(2)根据(1)中的等量关系,解决下列问题:
①已知,,求的值;
②已知,求的值.
19.阅读材料:若m2-2mn+2n2-8n+16=0,求m,n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,(m-n)2+(n-4)2=0,
∴(m-n)2=0,(n-4)2=0,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知△ABC的三边长a,b,c,且满足a2+b2-10a-12b+61=0,求c的取值范围;
(2)已知P=2x2+4y+13,Q=x2-y2+6x-1,比较P,Q的大小.
20.去年,某校为提升学生综合素质,推出了一系列校本课程,“蔬菜种植课”上,张老师用两条宽均为y米的小道将一块长(3x+y)米,宽(3x-y)米的长方形分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分(如图①的形状).
(1)求图①中两条小道的面积之和并化简;
(2)由于去年学生报名人数有限,张老师只要求学生们在Ⅰ部分土地上种植A型蔬菜,在Ⅱ部分土地上种植B型蔬菜,已知种植A型蔬菜每平方米的产量是6千克,种植B型蔬菜每平方米的产量是4千克,求去年种植蔬菜的总产量并化简;
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【详解】
A. (x+y)(﹣y+x)=x2﹣y2,故该选项正确,符合题意;
B. (﹣x+y)2=x2-2xy+y2,故该选项不正确,不符合题意;
C. (﹣x﹣y)2=x2+2xy+y2,故该选项不正确,不符合题意;
D. (x+y)(y﹣x)=y2﹣x2,故该选项不正确,不符合题意;
故选A
2.C
【详解】
解:∵,xy=3,
∴=(x+y)2 2xy=52 2×3=25 6=19,
故选:C.
3.A
【详解】:∵左图中阴影部分的面积是a2 b2,右图中梯形的面积是
(2a+2b)(a b)=(a+b)(a b),
∴a2 b2=(a+b)(a b).
故选:A.
4.B
解:由两边同时平方得:
,
∴;
故选:B.
5.B
解:、不存在互为相同和相反的项,不能用平方差公式计算,故本选项不符合题意;
B、是相同的项,互为相反项是与,符合平方差公式的要求,故本选项符合题意;
C、a是相同的项,不存在相反的项,不能用平方差公式计算,故本选项错误 ;
D、 中符合完全平方公式,不能用平方差公式计算,故本选项错误.
故选B.
6.D
解:∵x+y=6,x2+y2=(x+y)2 2xy=20,
∴2xy=62 20=16,
∴xy=8,
∴(x y)2=x2+y2 2xy=20 2×8=4,
∴x y=±2,
故选:D.
7.D
解:∵x的二次三项式x2+kx+9可以写成一个完全平方式,
∴x2+kx+9=(x±3)2=x2±6x+9,
∴k=±6.
故选:D.
8.C
解:∵(a-b)2=6,
∴a2-2ab+b2=6①
∵(a+b)2=4,
∴a2+2ab+b2=4②
①+②得,2a2+2b2=10,
∴a2+b2=5
故选:C.
9.A
解:根据正方形的图形可知,阴影部分的面积为,
平行四边形的底边长为,高为,
故平行四边形的面积为,
由此可以得到一个关于,的恒等式是,
故选:C.
10.B
解:设a=m-53,b=m-47,则ab=25,a-b=-6,
∴a2+b2=(a-b)2+2ab=(-6)2+50=86,
∴(m-53)2+(m-47)2=86,
故选:B.
11.3
解:∵,
∴,即 ①,
∵,
∴②,
由①-②,得: ,
解得:.
故答案为:3.
12.25
解:(1),即:,
(2),即:,
故答案为:(1)25;;(2);.
13.±2
解:∵(s-t)2=s2-2st+t2=10-6=4,
∴s-t=±2,
故答案为:±2.
14.8
解:设长方形的长为a,宽为b,
由图1可得, 4ab=35,
即=2ab+35①,
由图2可得,(2a+b)(a+2b) 5ab=102,
即=51②,
由①②得,2ab+35=51,
所以ab=8,
即长方形的面积为8,
故答案为:8.
15.(1);(2).
解:(1)
(2)
16.(1)=;(2)不同意,理由见详解.
解:(1),
=,
=;
(2)不同意,理由如下
=,
∵,
∴,
∴随着x取不同的数,的值总是正数.
∴嘉琪的说法不正确,不同意他的说法.
17.(1)39999;(2)1
(1)原式=(200-1)×(200+1)
=2002-12
=40000-1
=39999;
(2)20132﹣(2013+1)×(2013-1)
=20132-20132+1
=1.
18.(1);(2)①3,②
解:(1).
(2)①,
.
.
,
.
②设,则,.
,
.
.
.
.
即.
.
19.(1)1<c<11;(2)P>Q.
解:(1)∵a2+b2-10a-12b+61=0,
∴a2-10a+25+b2-12b+36=0,
∴(a-5)2+(b-6)2=0,
∵(a-5)2≥0,(b-6)2≥0,
∴a-5=0,b-6=0,
解得:a=5,b=6,
∵a,b,c,是△ABC的三边长,
∴6-5<c<6+5,
即:1<c<11;
(2)由题知P-Q=2x2+4y+13-(x2-y2+6x-1)
=x2-6x+9+y2+4y+4+1
=(x-3)2+(y+2)2+1>0,
∴P>Q.
20.(1)图①中两条小道的面积之和为米2;(2)去年种植蔬菜的总产量为.
解:(1)两条小道的面积之和:
;
∴两条小道的面积之和为米2;
(2)根据题意,
.
