贵州兴义六中2012-2013学年高二上学期8月月考数学(文)试题
文档属性
| 名称 | 贵州兴义六中2012-2013学年高二上学期8月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-13 08:21:53 | ||
图片预览



文档简介
贵州兴义六中2012-2013学年高二上学期8月月考--数学(文)
I 卷
一、选择题
1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )
A. 一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
【答案】D
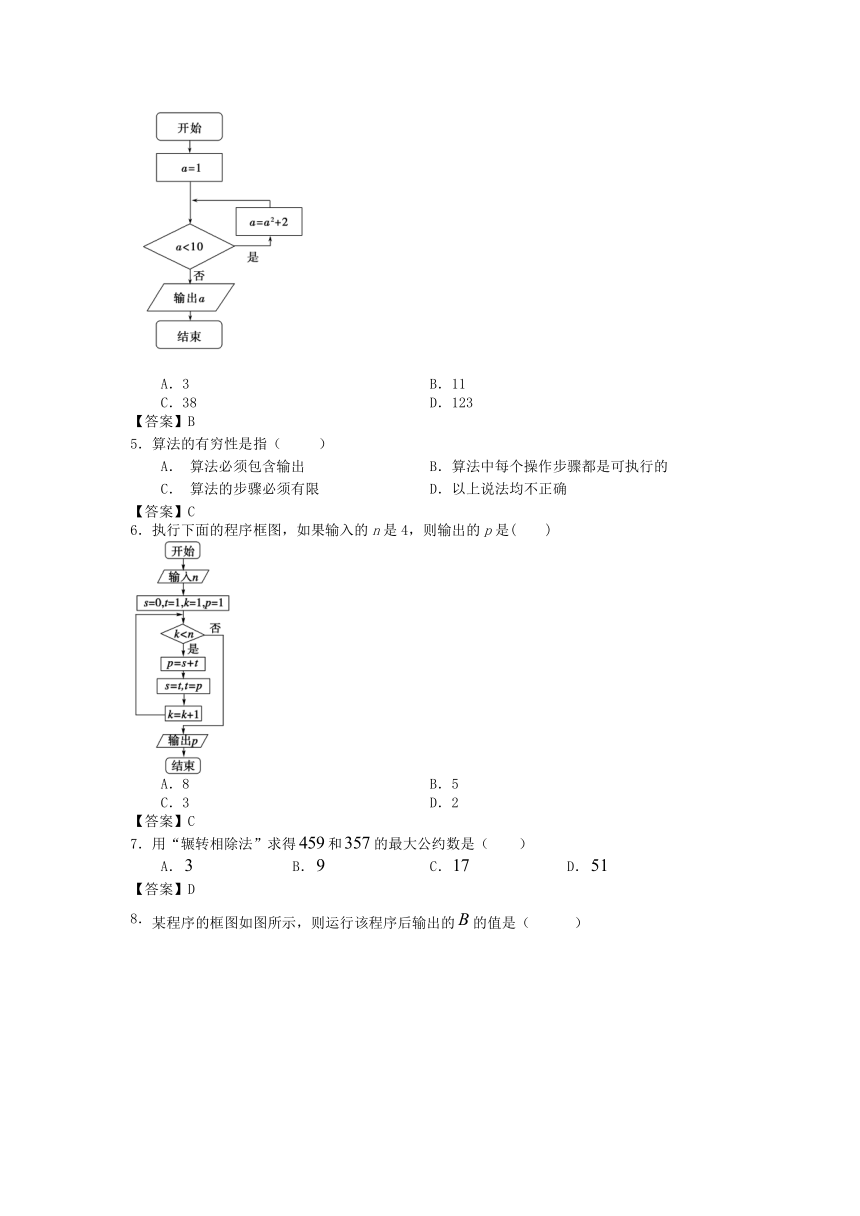
2.阅读如图21-5所示的程序框图,输出的结果S的值为( )
图21-5
A.0 B. C. D.-
【答案】B
3.执行如图所示的程序框图,输出的S值为( )
A. B. C. D.
【答案】A
4.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )
A.3 B.11
C.38 D.123
【答案】B
5.算法的有穷性是指( )
A. 算法必须包含输出 B.算法中每个操作步骤都是可执行的
C. 算法的步骤必须有限 D.以上说法均不正确
【答案】C
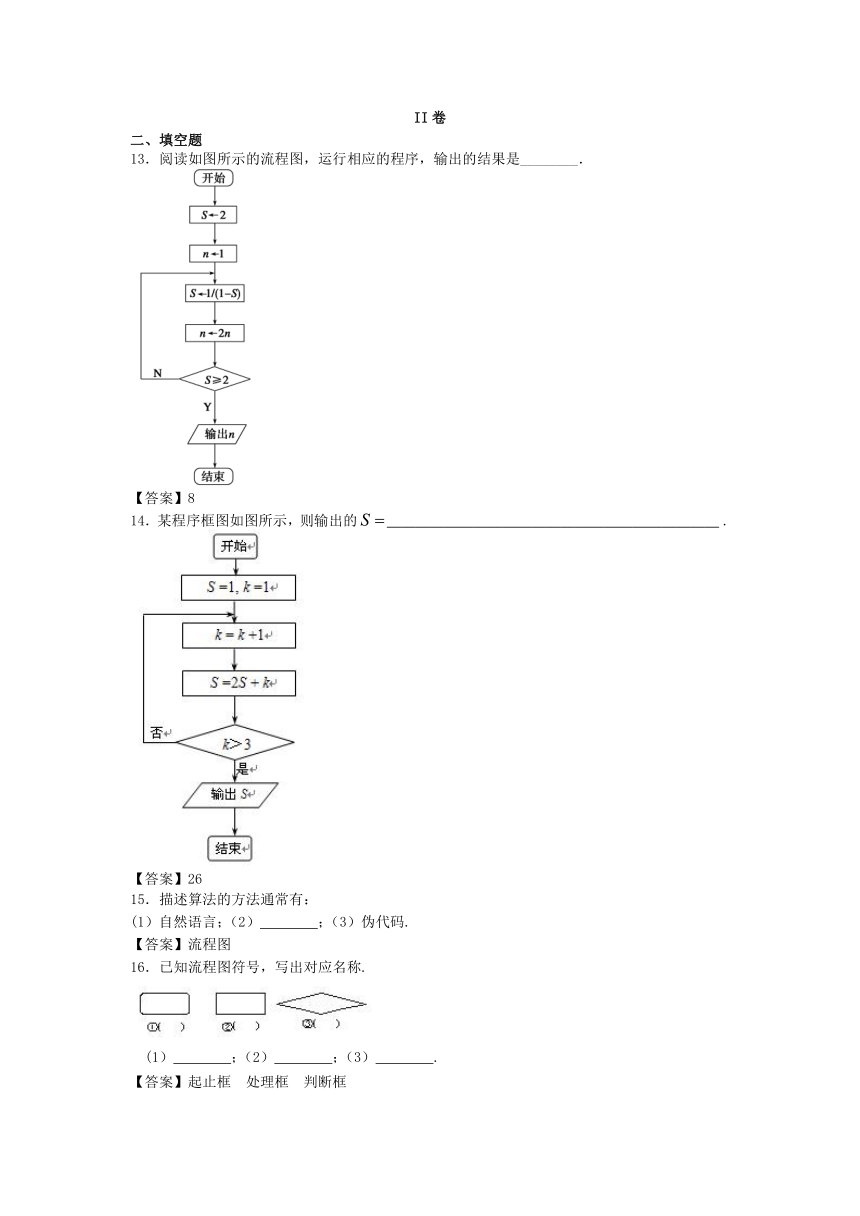
6.执行下面的程序框图,如果输入的n是4,则输出的p是( )
A.8 B.5
C.3 D.2
【答案】C
7.用“辗转相除法”求得和的最大公约数是( )
A. B. C. D.
【答案】D
8.某程序的框图如图所示,则运行该程序后输出的的值是( )
A.
B.
C.
D.
【答案】A
9.下列给出的赋值语句中正确的是( )
A.3=A B. M=-M C. B=A=2 D.
【答案】B
10.下列运算不属于我们所讨论算法范畴的是( )
A.已知圆的半径求圆的面积
B.随意抽4张扑克牌算到二十四点的可能性
C.已知坐标平面内两点求直线方程
D.加减乘除法运算法则
【答案】B
11.用秦九韶算法求n 次多项式,当时,求需要算乘方、乘法、加法的次数分别为( )
A. B.n,2n,n C. 0,2n,n D. 0,n,n
【答案】D
12.下列程序执行后输出的结果是( )
A. –1 B. 0 C. 1 D. 2
【答案】B
II卷
二、填空题
13.阅读如图所示的流程图,运行相应的程序,输出的结果是________.
【答案】8
14.某程序框图如图所示,则输出的 .
【答案】26
15.描述算法的方法通常有:
(1)自然语言;(2) ;(3)伪代码.
【答案】流程图
16.已知流程图符号,写出对应名称.
(1) ;(2) ;(3) .
【答案】起止框 处理框 判断框
三、解答题
17. 写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
【答案】用二分法求方程的近似值一般取区间[a,b]具有以下特征:
f(a)<0,f(b)>0. 由于f(1)=13-1-1=-1<0,
f(1.5)=1.53-1.5-1=0.875>0,
所以取[1,1.5]中点=1.25研究,以下同求x2-2=0的根的方法.
相应的程序框图是:
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
18.某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:
(1)写出该城市人口数y(万人)与年份x(年)的函数关系式;
(2)表示计算10年以后该城市人口总数的算法;
(3)用流程图表示计算大约多少年以后该城市人口将达到120万人的算法。
【答案】(1)
(2)法1
Rrint y
法2
(3)分析:即求满足的最小正整数n,其算法流程图如下:
19.用秦九韶算法求多项式
当时的值。写出其算法,写出相应的程序语句.
【答案】
20. 用冒泡排序法将下列各数排成一列:8,6,3,18,21,67,54.
并写出各趟的最后结果及各趟完成交换的次数.
【答案】每一趟都从头开始,两个两个地比较,若前者小,则两数位置不变;否则,调整这两个数的位置.
第一趟的结果是:6 3 8 18 21 54 67
完成3次交换.
第二趟的结果是:3 6 8 18 21 54 67
完成1次交换.
第三趟交换次数为0,说明已排好次序,
即3 6 8 18 21 54 67.
21. 我国《算经十书》之一《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?答曰:二十三.”你
能用程序解决这个问题吗?
【答案】设物共m个,被3,5,7除所得的商分别为x、y、z,则这个问题相当于求不定方程
的正整数解.
m应同时满足下列三个条件:(1)m MOD 3=2;(2)m MOD 5=3;
(3)m MOD 7=2.因此,可以让m从2开始检验,若3个条件中有任何一个不成立,则m递增1,一直到m同时满足三个条件为止.
程序:m=2
f=0
WHILE f=0
IF m MOD 3=2 AND m MOD 5=3
AND m MOD 7=2 THEN
PRINT “物体的个数为:”;m
f=1
ELSE
m=m+1
END IF
WEND
END
22.将十进制数30化为二进制.
【答案】把一个十进制的数转换为相应的二进制数,用2反复去除欲被转换的十进制数30,直到商是0为止,所得余数(从末位读起)就是该十进制数30的二进制表示. 所以
I 卷
一、选择题
1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )
A. 一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
【答案】D
2.阅读如图21-5所示的程序框图,输出的结果S的值为( )
图21-5
A.0 B. C. D.-
【答案】B
3.执行如图所示的程序框图,输出的S值为( )
A. B. C. D.
【答案】A
4.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )
A.3 B.11
C.38 D.123
【答案】B
5.算法的有穷性是指( )
A. 算法必须包含输出 B.算法中每个操作步骤都是可执行的
C. 算法的步骤必须有限 D.以上说法均不正确
【答案】C
6.执行下面的程序框图,如果输入的n是4,则输出的p是( )
A.8 B.5
C.3 D.2
【答案】C
7.用“辗转相除法”求得和的最大公约数是( )
A. B. C. D.
【答案】D
8.某程序的框图如图所示,则运行该程序后输出的的值是( )
A.
B.
C.
D.
【答案】A
9.下列给出的赋值语句中正确的是( )
A.3=A B. M=-M C. B=A=2 D.
【答案】B
10.下列运算不属于我们所讨论算法范畴的是( )
A.已知圆的半径求圆的面积
B.随意抽4张扑克牌算到二十四点的可能性
C.已知坐标平面内两点求直线方程
D.加减乘除法运算法则
【答案】B
11.用秦九韶算法求n 次多项式,当时,求需要算乘方、乘法、加法的次数分别为( )
A. B.n,2n,n C. 0,2n,n D. 0,n,n
【答案】D
12.下列程序执行后输出的结果是( )
A. –1 B. 0 C. 1 D. 2
【答案】B
II卷
二、填空题
13.阅读如图所示的流程图,运行相应的程序,输出的结果是________.
【答案】8
14.某程序框图如图所示,则输出的 .
【答案】26
15.描述算法的方法通常有:
(1)自然语言;(2) ;(3)伪代码.
【答案】流程图
16.已知流程图符号,写出对应名称.
(1) ;(2) ;(3) .
【答案】起止框 处理框 判断框
三、解答题
17. 写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
【答案】用二分法求方程的近似值一般取区间[a,b]具有以下特征:
f(a)<0,f(b)>0. 由于f(1)=13-1-1=-1<0,
f(1.5)=1.53-1.5-1=0.875>0,
所以取[1,1.5]中点=1.25研究,以下同求x2-2=0的根的方法.
相应的程序框图是:
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
18.某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:
(1)写出该城市人口数y(万人)与年份x(年)的函数关系式;
(2)表示计算10年以后该城市人口总数的算法;
(3)用流程图表示计算大约多少年以后该城市人口将达到120万人的算法。
【答案】(1)
(2)法1
Rrint y
法2
(3)分析:即求满足的最小正整数n,其算法流程图如下:
19.用秦九韶算法求多项式
当时的值。写出其算法,写出相应的程序语句.
【答案】
20. 用冒泡排序法将下列各数排成一列:8,6,3,18,21,67,54.
并写出各趟的最后结果及各趟完成交换的次数.
【答案】每一趟都从头开始,两个两个地比较,若前者小,则两数位置不变;否则,调整这两个数的位置.
第一趟的结果是:6 3 8 18 21 54 67
完成3次交换.
第二趟的结果是:3 6 8 18 21 54 67
完成1次交换.
第三趟交换次数为0,说明已排好次序,
即3 6 8 18 21 54 67.
21. 我国《算经十书》之一《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?答曰:二十三.”你
能用程序解决这个问题吗?
【答案】设物共m个,被3,5,7除所得的商分别为x、y、z,则这个问题相当于求不定方程
的正整数解.
m应同时满足下列三个条件:(1)m MOD 3=2;(2)m MOD 5=3;
(3)m MOD 7=2.因此,可以让m从2开始检验,若3个条件中有任何一个不成立,则m递增1,一直到m同时满足三个条件为止.
程序:m=2
f=0
WHILE f=0
IF m MOD 3=2 AND m MOD 5=3
AND m MOD 7=2 THEN
PRINT “物体的个数为:”;m
f=1
ELSE
m=m+1
END IF
WEND
END
22.将十进制数30化为二进制.
【答案】把一个十进制的数转换为相应的二进制数,用2反复去除欲被转换的十进制数30,直到商是0为止,所得余数(从末位读起)就是该十进制数30的二进制表示. 所以
同课章节目录
