贵州兴枣中学2012-2013学年高二上学期8月月考数学(理)试题
文档属性
| 名称 | 贵州兴枣中学2012-2013学年高二上学期8月月考数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 224.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-13 08:22:41 | ||
图片预览

文档简介
贵州兴枣中学2012-2013学年高二上学期8月月考--数学(理)
I 卷
一、选择题
1.给出以下四个数:6,-3,0,15,用冒泡排序法将它们按从大到小的顺序排列需要经过几趟( )
A.1
B. 2
C. 3
D. 4
【答案】C
2.当时,下面的程序段执行后所得的结果是 ( )
A. B. C. D.
【答案】C
3.当时,下面的程序段输出的结果是( )
A. B. C. D.
【答案】D
4.算法的有穷性是指( )
A. 算法必须包含输出 B.算法中每个操作步骤都是可执行的
C. 算法的步骤必须有限 D.以上说法均不正确
【答案】C
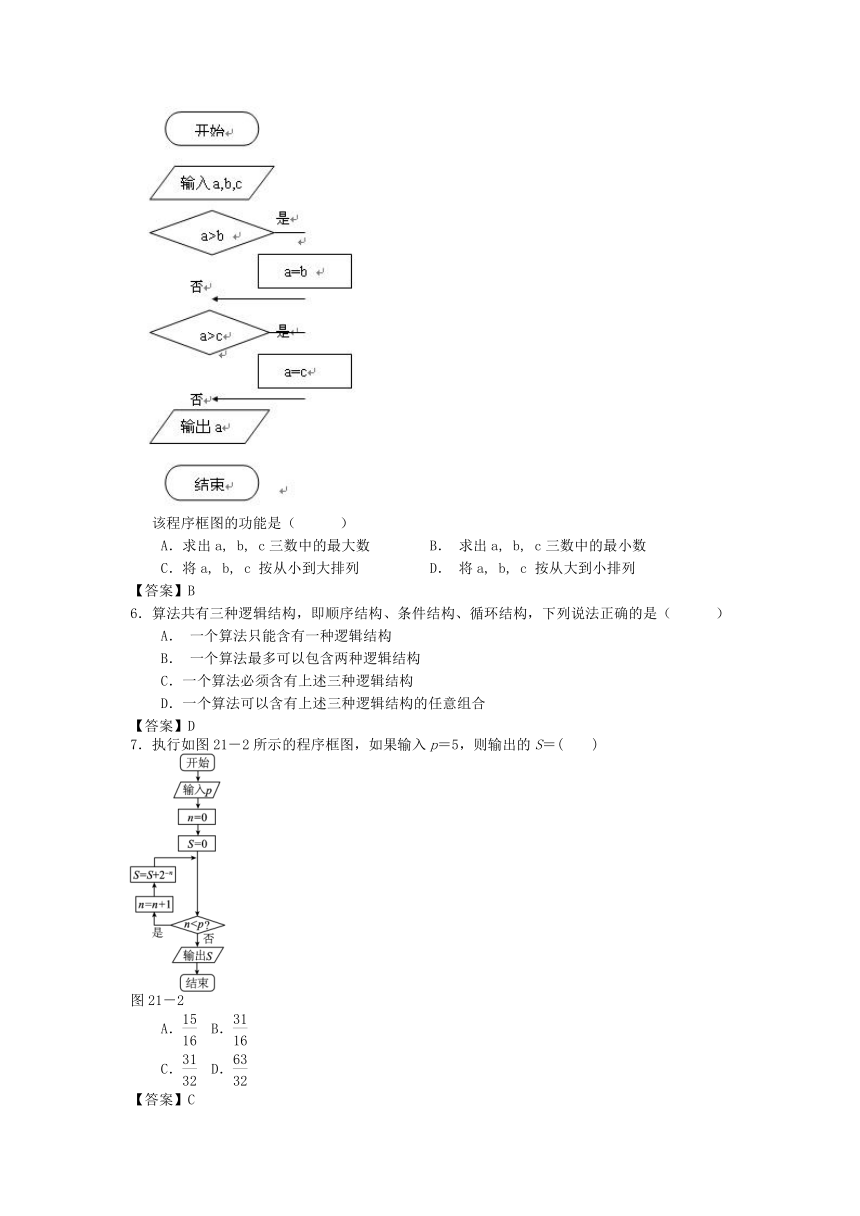
5.给出以下一个算法的程序框图(如图所示):
该程序框图的功能是( )
A.求出a, b, c三数中的最大数 B. 求出a, b, c三数中的最小数
C.将a, b, c 按从小到大排列 D. 将a, b, c 按从大到小排列
【答案】B
6.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )
A. 一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
【答案】D
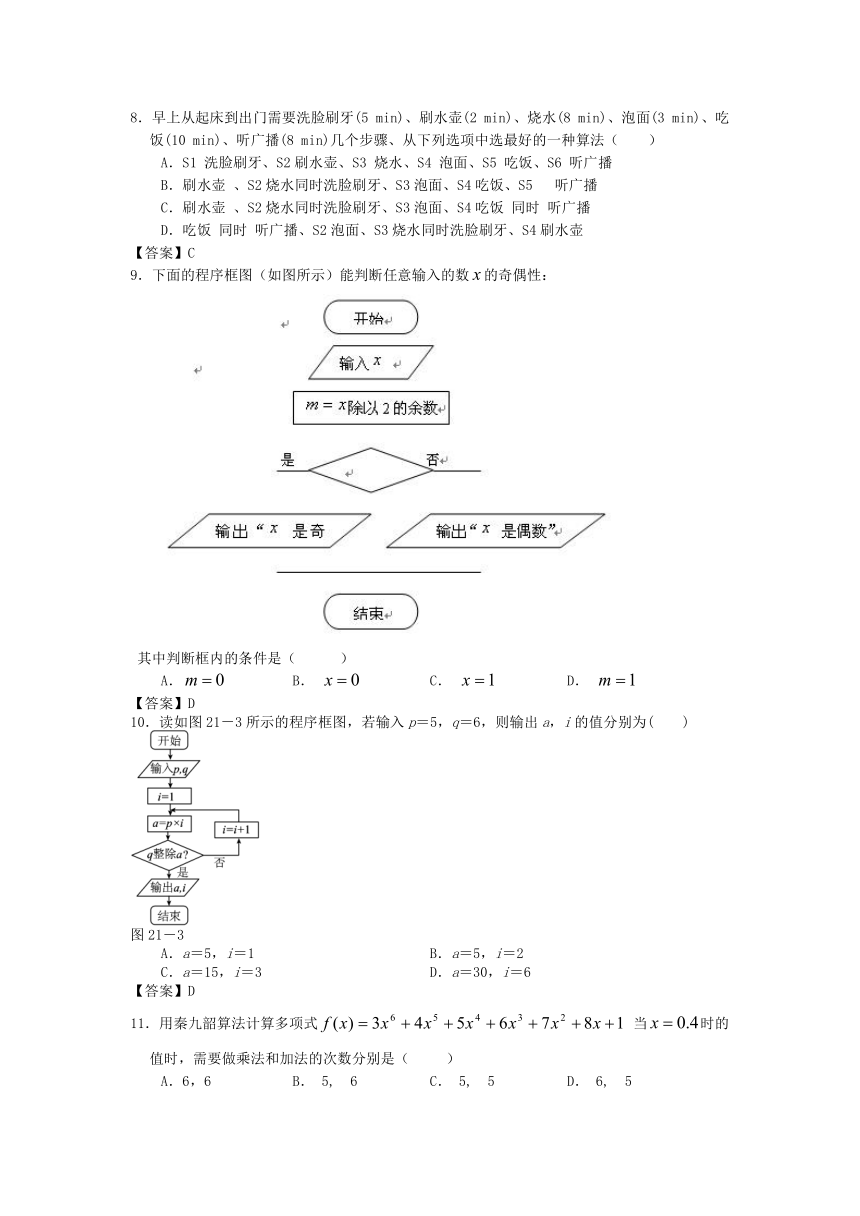
7.执行如图21-2所示的程序框图,如果输入p=5,则输出的S=( )
图21-2
A. B.
C. D.
【答案】C
8.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法( )
A.S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播
B.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播
C.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播
D.吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶
【答案】C
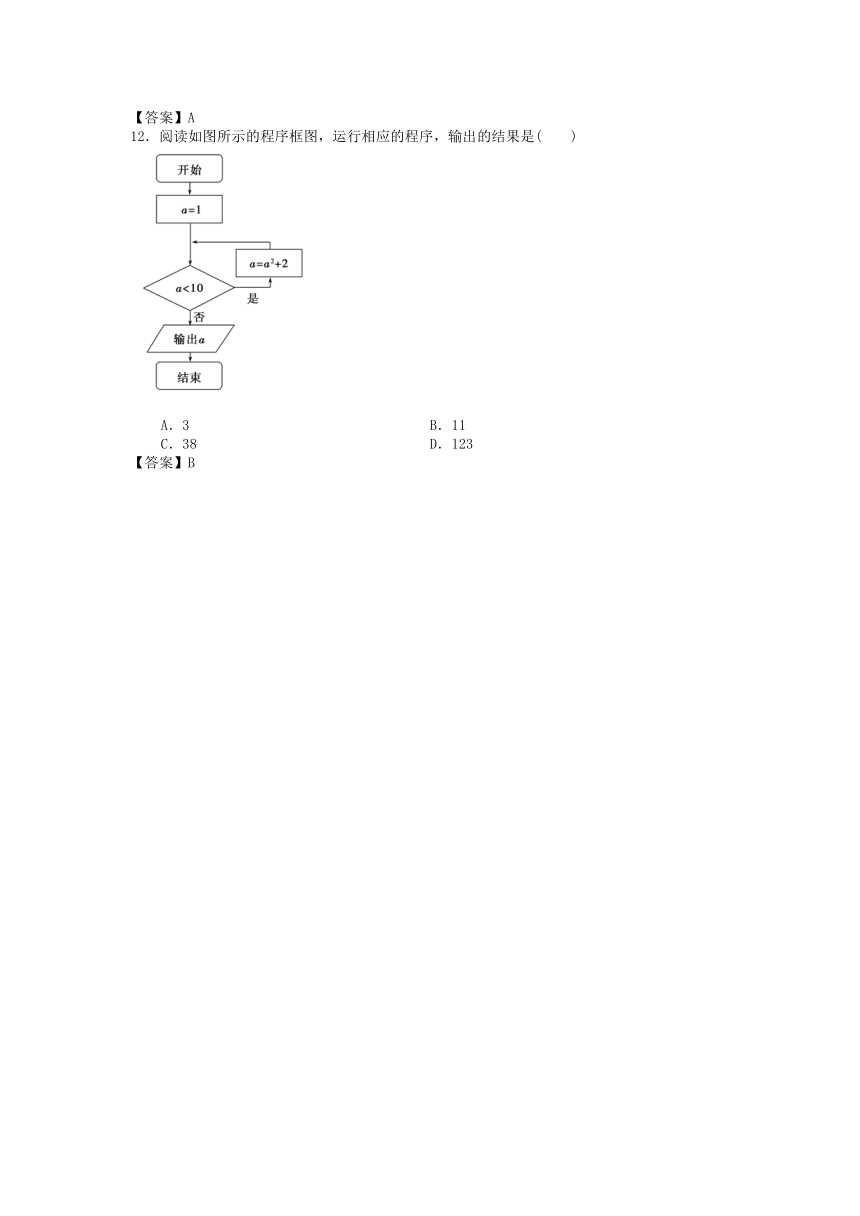
9.下面的程序框图(如图所示)能判断任意输入的数的奇偶性:
其中判断框内的条件是( )
A. B. C. D.
【答案】D
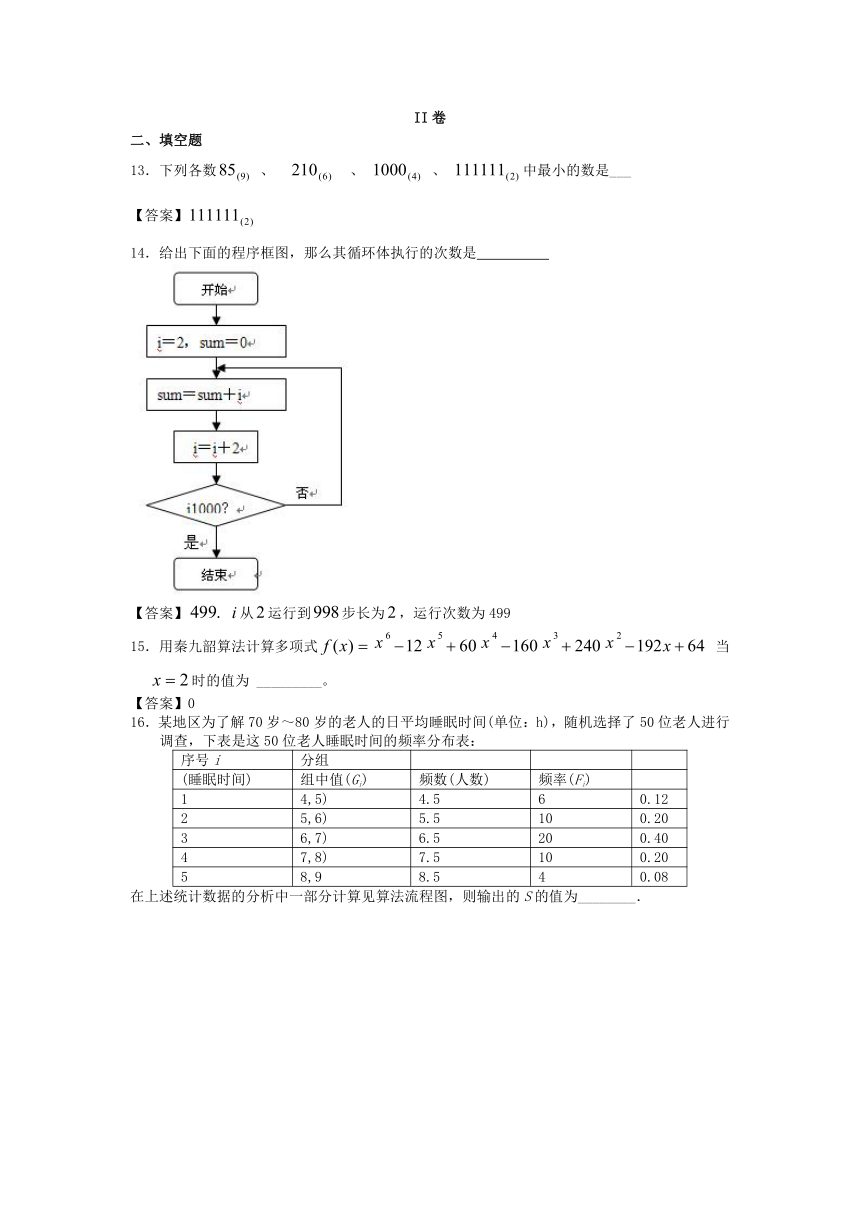
10.读如图21-3所示的程序框图,若输入p=5,q=6,则输出a,i的值分别为( )
图21-3
A.a=5,i=1 B.a=5,i=2
C.a=15,i=3 D.a=30,i=6
【答案】D
11.用秦九韶算法计算多项式 当时的值时,需要做乘法和加法的次数分别是( )
A.6,6 B. 5, 6 C. 5, 5 D. 6, 5
【答案】A
12.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )
A.3 B.11
C.38 D.123
【答案】B
II卷
二、填空题
13.下列各数 、 、 、 中最小的数是___
【答案】
14.给出下面的程序框图,那么其循环体执行的次数是
【答案】 从运行到步长为,运行次数为499
15.用秦九韶算法计算多项式 当时的值为 _________。
【答案】0
16.某地区为了解70岁~80岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
序号i 分组
(睡眠时间) 组中值(Gi) 频数(人数) 频率(Fi)
1 4,5) 4.5 6 0.12
2 5,6) 5.5 10 0.20
3 6,7) 6.5 20 0.40
4 7,8) 7.5 10 0.20
5 8,9 8.5 4 0.08
在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为________.
【答案】6.42
三、解答题
17. 写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
【答案】
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
18. 2000年我国人口为13亿,如果人口每年的自然增长率为7‰,那么多少年
后我国人口将达到15亿?设计一个算法的程序.
【答案】A=13
R=0.007
i=1
DO
A=A*(1+R)
i=i+1
LOOP UNTIL A>=15
i=i-1
PRINT “达到或超过15亿人口需要的年数为:”;i
END
19. 写出下列程序运行的结果.
(1)a=2 (2)x=100
i=1 i=1
WHILE i<=6 DO
a=a+1 x=x+10
PRINT i,a PRINT i,x
i=i+1 i=i+1
WEND LOOP UNTIL x=200
END END
【答案】(1)1,3;2,4;3,5;4,6;5,7;6,8.
(2)1,110;2,120;3,130;4,140;5,150;6,160;7,170;8,180; 9,190;10,200.
20. 求两个底面半径分别为1和4,且高为4的圆台的表面积及体积,写出该问题的一个算法,并画出流程图.
【答案】算法设计如下:
S1 r1←1,r2←4,h←4;
S2 l←;
S3 S1←πr,S2←πr,S3←π(r1+r2)l;
S4 S←S1+S2+S3,
V← (S1++S2)h;
S5 输出S和V.
该算法的流程图如下:
21.用秦九韶算法求多项式
当时的值。写出其算法,写出相应的程序语句.
【答案】
22. 我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一凡百钱,买鸡百只,问鸡翁、母、雏各几何?”你能用程序解决这个问题吗?
【答案】设鸡翁、母、雏各x、y、z只,则
由②,得z=100-x-y, ③
③代入①,得5x+3y+=100,
7x+4y=100. ④
求方程④的解,可由程序解之.
程序:x=1
y=1
WHILE x<=14
WHILE y<=25
IF 7*x+4*y=100 THEN
z=100-x-y
PRINT “鸡翁、母、雏的个数别为:”;x,y,z
END IF
y=y+1
WEND
x=x+1
y=1
WEND
END
(法二)实际上,该题可以不对方程组进行化简,通过设置多重循环的方式得以实现.由①、②可得x最大值为20,y最大值为33,z最大值为100,且z为3的倍数.程序如下:
x=1
y=1
z=3
WHILE x<=20
WHILE y<=33
WHILE z<=100
IF 5*x+3*y+z3=100 AND
x+y+z=100 THEN
PRINT “鸡翁、母、雏的个数分别为:”;x、y、z
END IF
z=z+3
WEND
y=y+1
z=3
WEND
x=x+1
y=1
WEND
END
I 卷
一、选择题
1.给出以下四个数:6,-3,0,15,用冒泡排序法将它们按从大到小的顺序排列需要经过几趟( )
A.1
B. 2
C. 3
D. 4
【答案】C
2.当时,下面的程序段执行后所得的结果是 ( )
A. B. C. D.
【答案】C
3.当时,下面的程序段输出的结果是( )
A. B. C. D.
【答案】D
4.算法的有穷性是指( )
A. 算法必须包含输出 B.算法中每个操作步骤都是可执行的
C. 算法的步骤必须有限 D.以上说法均不正确
【答案】C
5.给出以下一个算法的程序框图(如图所示):
该程序框图的功能是( )
A.求出a, b, c三数中的最大数 B. 求出a, b, c三数中的最小数
C.将a, b, c 按从小到大排列 D. 将a, b, c 按从大到小排列
【答案】B
6.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )
A. 一个算法只能含有一种逻辑结构
B. 一个算法最多可以包含两种逻辑结构
C.一个算法必须含有上述三种逻辑结构
D.一个算法可以含有上述三种逻辑结构的任意组合
【答案】D
7.执行如图21-2所示的程序框图,如果输入p=5,则输出的S=( )
图21-2
A. B.
C. D.
【答案】C
8.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个步骤、从下列选项中选最好的一种算法( )
A.S1 洗脸刷牙、S2刷水壶、S3 烧水、S4 泡面、S5 吃饭、S6 听广播
B.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5 听广播
C.刷水壶 、S2烧水同时洗脸刷牙、S3泡面、S4吃饭 同时 听广播
D.吃饭 同时 听广播、S2泡面、S3烧水同时洗脸刷牙、S4刷水壶
【答案】C
9.下面的程序框图(如图所示)能判断任意输入的数的奇偶性:
其中判断框内的条件是( )
A. B. C. D.
【答案】D
10.读如图21-3所示的程序框图,若输入p=5,q=6,则输出a,i的值分别为( )
图21-3
A.a=5,i=1 B.a=5,i=2
C.a=15,i=3 D.a=30,i=6
【答案】D
11.用秦九韶算法计算多项式 当时的值时,需要做乘法和加法的次数分别是( )
A.6,6 B. 5, 6 C. 5, 5 D. 6, 5
【答案】A
12.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )
A.3 B.11
C.38 D.123
【答案】B
II卷
二、填空题
13.下列各数 、 、 、 中最小的数是___
【答案】
14.给出下面的程序框图,那么其循环体执行的次数是
【答案】 从运行到步长为,运行次数为499
15.用秦九韶算法计算多项式 当时的值为 _________。
【答案】0
16.某地区为了解70岁~80岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
序号i 分组
(睡眠时间) 组中值(Gi) 频数(人数) 频率(Fi)
1 4,5) 4.5 6 0.12
2 5,6) 5.5 10 0.20
3 6,7) 6.5 20 0.40
4 7,8) 7.5 10 0.20
5 8,9 8.5 4 0.08
在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为________.
【答案】6.42
三、解答题
17. 写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
【答案】
程序:a=1
b=1.5
c=0.001
DO
x=(a+b)2
f(a)=a∧3-a-1
f(x)=x∧3-x-1
IF f(x)=0 THEN
PRINT “x=”;x
ELSE
IF f(a)*f(x)<0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS(a-b)<=c
PRINT “方程的一个近似解x=”;x
END
18. 2000年我国人口为13亿,如果人口每年的自然增长率为7‰,那么多少年
后我国人口将达到15亿?设计一个算法的程序.
【答案】A=13
R=0.007
i=1
DO
A=A*(1+R)
i=i+1
LOOP UNTIL A>=15
i=i-1
PRINT “达到或超过15亿人口需要的年数为:”;i
END
19. 写出下列程序运行的结果.
(1)a=2 (2)x=100
i=1 i=1
WHILE i<=6 DO
a=a+1 x=x+10
PRINT i,a PRINT i,x
i=i+1 i=i+1
WEND LOOP UNTIL x=200
END END
【答案】(1)1,3;2,4;3,5;4,6;5,7;6,8.
(2)1,110;2,120;3,130;4,140;5,150;6,160;7,170;8,180; 9,190;10,200.
20. 求两个底面半径分别为1和4,且高为4的圆台的表面积及体积,写出该问题的一个算法,并画出流程图.
【答案】算法设计如下:
S1 r1←1,r2←4,h←4;
S2 l←;
S3 S1←πr,S2←πr,S3←π(r1+r2)l;
S4 S←S1+S2+S3,
V← (S1++S2)h;
S5 输出S和V.
该算法的流程图如下:
21.用秦九韶算法求多项式
当时的值。写出其算法,写出相应的程序语句.
【答案】
22. 我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一凡百钱,买鸡百只,问鸡翁、母、雏各几何?”你能用程序解决这个问题吗?
【答案】设鸡翁、母、雏各x、y、z只,则
由②,得z=100-x-y, ③
③代入①,得5x+3y+=100,
7x+4y=100. ④
求方程④的解,可由程序解之.
程序:x=1
y=1
WHILE x<=14
WHILE y<=25
IF 7*x+4*y=100 THEN
z=100-x-y
PRINT “鸡翁、母、雏的个数别为:”;x,y,z
END IF
y=y+1
WEND
x=x+1
y=1
WEND
END
(法二)实际上,该题可以不对方程组进行化简,通过设置多重循环的方式得以实现.由①、②可得x最大值为20,y最大值为33,z最大值为100,且z为3的倍数.程序如下:
x=1
y=1
z=3
WHILE x<=20
WHILE y<=33
WHILE z<=100
IF 5*x+3*y+z3=100 AND
x+y+z=100 THEN
PRINT “鸡翁、母、雏的个数分别为:”;x、y、z
END IF
z=z+3
WEND
y=y+1
z=3
WEND
x=x+1
y=1
WEND
END
同课章节目录
