冀教版七年级数学上册1.8.2有理数的乘法运算律 课件(共22张PPT)
文档属性
| 名称 | 冀教版七年级数学上册1.8.2有理数的乘法运算律 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 987.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 14:40:36 | ||
图片预览








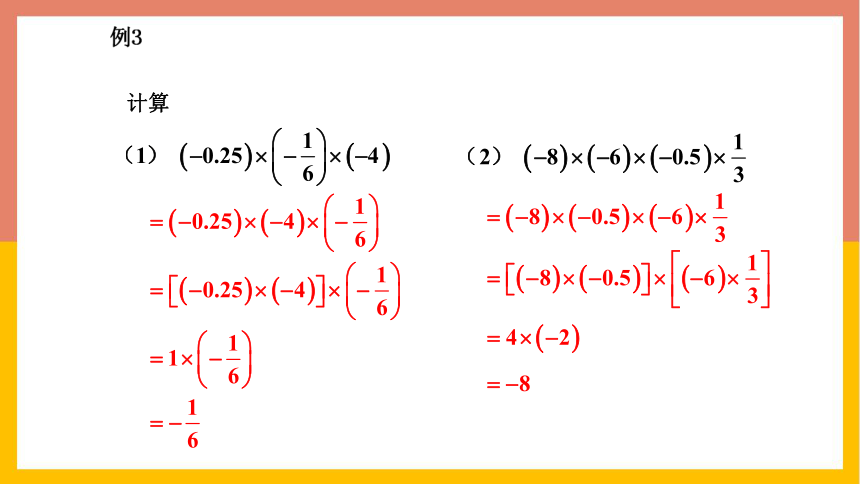
文档简介
(共22张PPT)
有理数的乘法运算律
有理数的乘法运算律
有理数的乘法运算律
学习目标
1、理解有理数乘法的运算律,能利用有理数乘法的运算律进行有理数乘法运算;
2、掌握多个有理数相乘的符号法则.
重难点
有理数的乘法运算律。
重点
多个有理数相乘的符号法则。
难点
探究
3、小学时候大家学过乘法的那些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,仍得0.
先确定积的符号; 再计算绝对值的积.
乘法交换律、乘法结合律、乘法对加法的分配律
1、有理数乘法法则是什么?
2、如何进行有理数的乘法运算?
探究
计算:
通过以上结果思考,乘法交换律在有理数范围还成立吗?
计算:
通过以上结果思考,乘法结合律在有理数范围还成立吗?
探究
计算:
通过以上结果思考,乘法对加法的分配律在有理数范围还成立吗?
探究
运算律
事实上,在有理数范围内,乘法运算律仍然成立:
乘法交换律:ab=ba.
乘法结合律:(ab)c=a(bc).
乘法对加法的分配律(简称分配律):a(b+c)=ab+ac.
例3
计算
例4
计算
小结
(1)运用乘法的交换律、结合律时要连同符号一起交换、结合,否则容易出现错误;
(2)利用分配律时,不能把运算符号和性质符号混淆.
探究
计算并填写表格:
(1) (2) (3) (4) (5)
负因数的个数
积的符号
0
1
2
3
4
正
正
正
负
负
你发现了什么?
小结
几个不为0的数相乘,积的符号由__________________决定.
当负因数有_______个时,积为负;
当负因数有_______个时,积为正.
几个数相乘,如果有一个因数为0,_________
负因数的个数
奇数
偶数
积就为0.
奇负偶正
随堂练习
计算
随堂练习
计算
随堂练习
计算
分配律的逆运用
基础巩固
1.计算时,应该运用( ).
A.加法交换律 B.乘法分配律
C.乘法交换律 D.乘法结合律
2.利用分配律计算时,正确的方案可以是( )
A.
B.
C.
D.
B
A
基础巩固
3.用简便方法计算下列各式的值:
(1)
通过改变负号的位置,使之符合分配律逆用的形式
基础巩固
3.用简便方法计算下列各式的值:
(2)
基础巩固
3.用简便方法计算下列各式的值:
(3)
课堂总结
有理数的乘法运算律
知识
考点
有理数的乘法运算
乘法的简便运算
简便运算
空白演示
单击输入您的封面副标题
谢 谢 聆 听
有理数的乘法运算律
有理数的乘法运算律
有理数的乘法运算律
学习目标
1、理解有理数乘法的运算律,能利用有理数乘法的运算律进行有理数乘法运算;
2、掌握多个有理数相乘的符号法则.
重难点
有理数的乘法运算律。
重点
多个有理数相乘的符号法则。
难点
探究
3、小学时候大家学过乘法的那些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,仍得0.
先确定积的符号; 再计算绝对值的积.
乘法交换律、乘法结合律、乘法对加法的分配律
1、有理数乘法法则是什么?
2、如何进行有理数的乘法运算?
探究
计算:
通过以上结果思考,乘法交换律在有理数范围还成立吗?
计算:
通过以上结果思考,乘法结合律在有理数范围还成立吗?
探究
计算:
通过以上结果思考,乘法对加法的分配律在有理数范围还成立吗?
探究
运算律
事实上,在有理数范围内,乘法运算律仍然成立:
乘法交换律:ab=ba.
乘法结合律:(ab)c=a(bc).
乘法对加法的分配律(简称分配律):a(b+c)=ab+ac.
例3
计算
例4
计算
小结
(1)运用乘法的交换律、结合律时要连同符号一起交换、结合,否则容易出现错误;
(2)利用分配律时,不能把运算符号和性质符号混淆.
探究
计算并填写表格:
(1) (2) (3) (4) (5)
负因数的个数
积的符号
0
1
2
3
4
正
正
正
负
负
你发现了什么?
小结
几个不为0的数相乘,积的符号由__________________决定.
当负因数有_______个时,积为负;
当负因数有_______个时,积为正.
几个数相乘,如果有一个因数为0,_________
负因数的个数
奇数
偶数
积就为0.
奇负偶正
随堂练习
计算
随堂练习
计算
随堂练习
计算
分配律的逆运用
基础巩固
1.计算时,应该运用( ).
A.加法交换律 B.乘法分配律
C.乘法交换律 D.乘法结合律
2.利用分配律计算时,正确的方案可以是( )
A.
B.
C.
D.
B
A
基础巩固
3.用简便方法计算下列各式的值:
(1)
通过改变负号的位置,使之符合分配律逆用的形式
基础巩固
3.用简便方法计算下列各式的值:
(2)
基础巩固
3.用简便方法计算下列各式的值:
(3)
课堂总结
有理数的乘法运算律
知识
考点
有理数的乘法运算
乘法的简便运算
简便运算
空白演示
单击输入您的封面副标题
谢 谢 聆 听
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
