冀教版七年级数学上册3.3代数式的值 课件(共26张PPT)
文档属性
| 名称 | 冀教版七年级数学上册3.3代数式的值 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 14:51:13 | ||
图片预览




文档简介
(共26张PPT)
代数式的值
代数式的值
代数式的值
1、会求代数式的值;
2、掌握代数式求值的实际应用.
学习目标
会求代数式的值。
重点
难点
重难点
掌握代数式求值的实际应用。
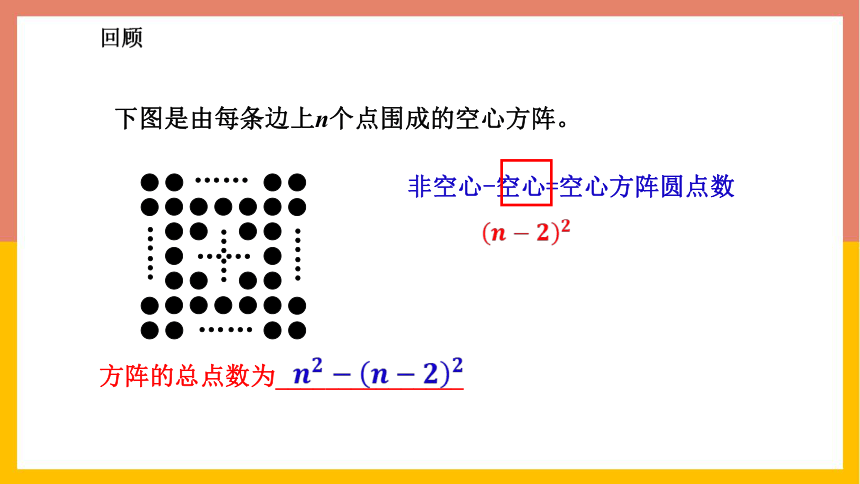
下图是由每条边上n个点围成的空心方阵。
……
……
……
……
方阵的总点数为_______________
非空心-空心=空心方阵圆点数
……
……
回顾
……
……
……
……
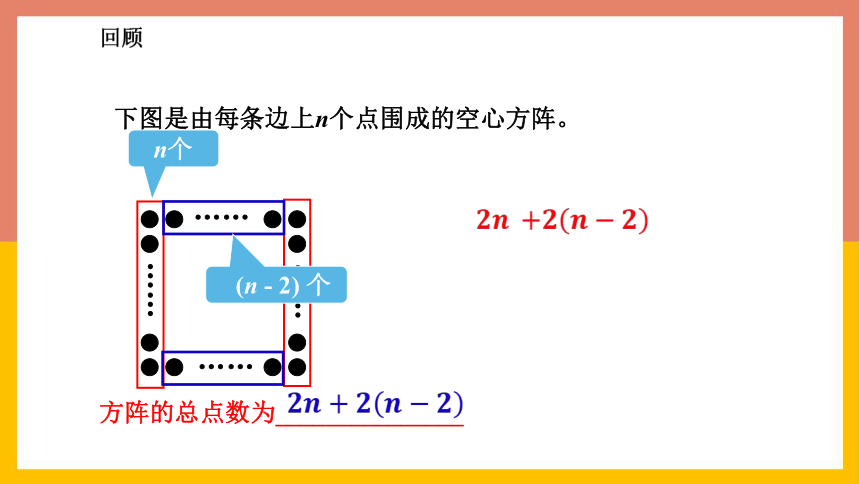
方阵的总点数为_______________
n个
(n - 2) 个
下图是由每条边上n个点围成的空心方阵。
回顾
……
……
……
……
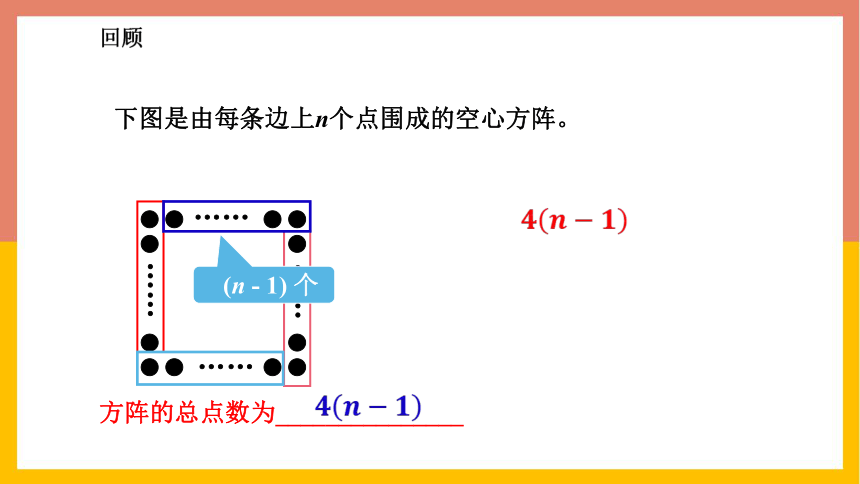
方阵的总点数为_______________
(n - 1) 个
下图是由每条边上n个点围成的空心方阵。
回顾
……
……
……
……
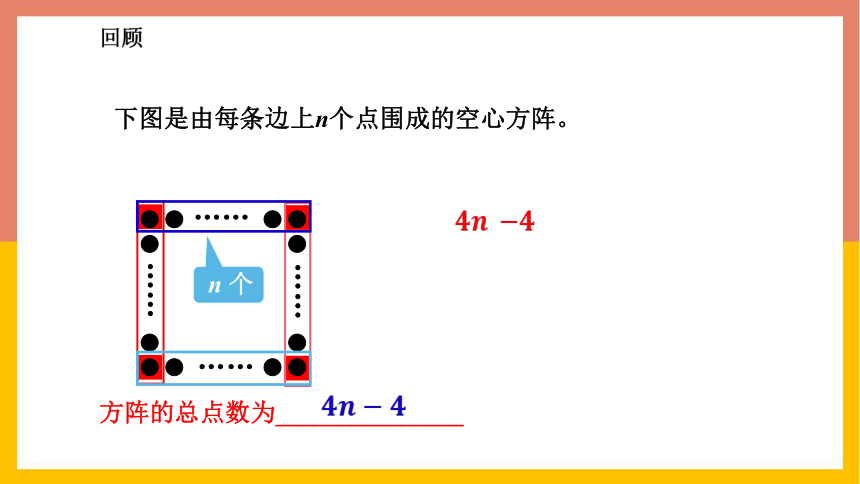
方阵的总点数为_______________
n 个
下图是由每条边上n个点围成的空心方阵。
回顾
这是一个含字母n的代数式.
当n取4,10,13等值时,分别代入上面的代数式,计算出代数式相应的值.
当时,
当时,
当时,
对于n的同一个取值,同学们得到的结果都相同吗?
探究
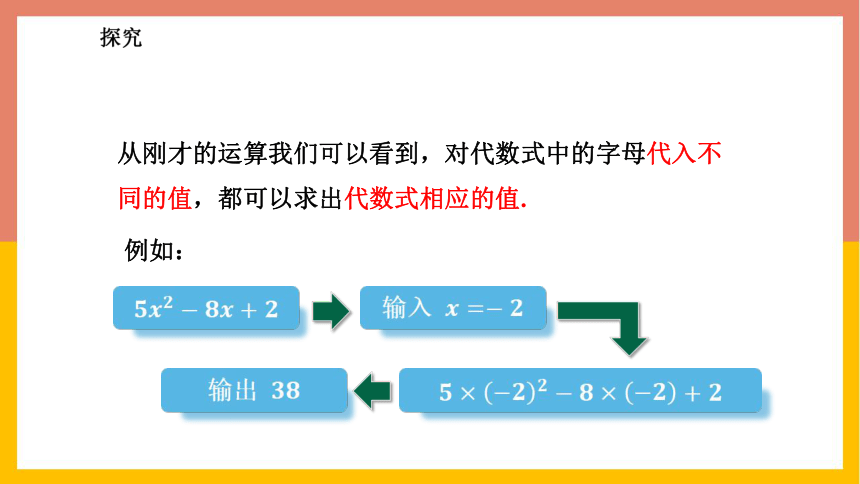
从刚才的运算我们可以看到,对代数式中的字母代入不同的值,都可以求出代数式相应的值.
例如:
输入
输出
探究
像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值。这个过程叫做求代数式的值.
代数式里的字母可以取不同的数值,但所取数值必须使代数式和它代表的实际数量有意义.比如中的v不能取0.
代数式的值
根据下面a,b的值,求代数式的值.
(1) (2)
解:(1)当时:
例1
根据下面a,b的值,求代数式的值.
(1) (2)
解:(1)当时:
例1
求代数式的值的步骤:
(1)写出条件:当……时;
(2)抄写代数式;
(3)代入数值;
(4)计算.
小结
(1)代入时,要“对号入座”,避免代错字母,其他符号不变;
(2)代数式中,代入数值以后原来省略的乘号一定要还原;
(3)若字母的值是负数或分数,将字母的值代入代数式时,应加上括号,原来的数字和运算符号都不能改变.
在代入数值时应注意:
小结
根据下面a,b的值,求代数式和的值.
(1) (2)
解:(1)当时:
随堂练习
根据下面a,b的值,求代数式和的值.
(1) (2)
解:(2)当时:
随堂练习
已知,则代数式的值为_________.
因为,将其整体代入得:
0
整体代入法
变式训练
如图,已知长方体的高为h,底面是边长为a的正方形。当h=3,a=2时,分别求其体积V和表面积S.
h
a
解:因为
所以,当时,
例2
小亮家离学校1280m,他每天步行上学,速度约是80m/min,我们用t(min)表示小亮从离开家开始的步行时间,s1(m)表示离开家的路程,s2 (m)表示距学校的路程.
(1)写出用 t 分别表示s1和s2的代数式;
s1 = _________________;
s2 = _________________.
练习
(2)对具体的 t 值,计算s1和s2的值,并填写下表;
t/min 0 4 5.5 10 12.5 16
s1/m
s2/m
0
1280
320
440
800
1000
1280
0
280
480
840
960
练习
(3)当t = 7时,请你比较小亮离家的路程与离学校的路程哪个远?
答:小亮离学校的路程更远。
练习
利用代数式的值解决实际问题时,可先根据实际问题列出代数式,然后根据已知字母的值求代数式的值,从而达到解决实际问题的目的.
小结
1、当, , 时代数式的值是( )
A.1 B. 2 C.3 D. 4
A
2、如果,那么=________.
3
基础巩固
3、堤坝的横截面是梯形,测得梯形上底为a=18m,下底b=36m,高h=20m,求这个截面的面积.
a
b
h
解:梯形面积公式为:
将a=18,b=36,h=20代入上面公式,得
答:堤坝的横截面积是540m2
基础巩固
知识
考点
根据问题列代数式,并求代数式的值
代数式的值的求法
课堂总结
空白演示
单击输入您的封面副标题
谢 谢 聆 听
代数式的值
代数式的值
代数式的值
1、会求代数式的值;
2、掌握代数式求值的实际应用.
学习目标
会求代数式的值。
重点
难点
重难点
掌握代数式求值的实际应用。
下图是由每条边上n个点围成的空心方阵。
……
……
……
……
方阵的总点数为_______________
非空心-空心=空心方阵圆点数
……
……
回顾
……
……
……
……
方阵的总点数为_______________
n个
(n - 2) 个
下图是由每条边上n个点围成的空心方阵。
回顾
……
……
……
……
方阵的总点数为_______________
(n - 1) 个
下图是由每条边上n个点围成的空心方阵。
回顾
……
……
……
……
方阵的总点数为_______________
n 个
下图是由每条边上n个点围成的空心方阵。
回顾
这是一个含字母n的代数式.
当n取4,10,13等值时,分别代入上面的代数式,计算出代数式相应的值.
当时,
当时,
当时,
对于n的同一个取值,同学们得到的结果都相同吗?
探究
从刚才的运算我们可以看到,对代数式中的字母代入不同的值,都可以求出代数式相应的值.
例如:
输入
输出
探究
像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值。这个过程叫做求代数式的值.
代数式里的字母可以取不同的数值,但所取数值必须使代数式和它代表的实际数量有意义.比如中的v不能取0.
代数式的值
根据下面a,b的值,求代数式的值.
(1) (2)
解:(1)当时:
例1
根据下面a,b的值,求代数式的值.
(1) (2)
解:(1)当时:
例1
求代数式的值的步骤:
(1)写出条件:当……时;
(2)抄写代数式;
(3)代入数值;
(4)计算.
小结
(1)代入时,要“对号入座”,避免代错字母,其他符号不变;
(2)代数式中,代入数值以后原来省略的乘号一定要还原;
(3)若字母的值是负数或分数,将字母的值代入代数式时,应加上括号,原来的数字和运算符号都不能改变.
在代入数值时应注意:
小结
根据下面a,b的值,求代数式和的值.
(1) (2)
解:(1)当时:
随堂练习
根据下面a,b的值,求代数式和的值.
(1) (2)
解:(2)当时:
随堂练习
已知,则代数式的值为_________.
因为,将其整体代入得:
0
整体代入法
变式训练
如图,已知长方体的高为h,底面是边长为a的正方形。当h=3,a=2时,分别求其体积V和表面积S.
h
a
解:因为
所以,当时,
例2
小亮家离学校1280m,他每天步行上学,速度约是80m/min,我们用t(min)表示小亮从离开家开始的步行时间,s1(m)表示离开家的路程,s2 (m)表示距学校的路程.
(1)写出用 t 分别表示s1和s2的代数式;
s1 = _________________;
s2 = _________________.
练习
(2)对具体的 t 值,计算s1和s2的值,并填写下表;
t/min 0 4 5.5 10 12.5 16
s1/m
s2/m
0
1280
320
440
800
1000
1280
0
280
480
840
960
练习
(3)当t = 7时,请你比较小亮离家的路程与离学校的路程哪个远?
答:小亮离学校的路程更远。
练习
利用代数式的值解决实际问题时,可先根据实际问题列出代数式,然后根据已知字母的值求代数式的值,从而达到解决实际问题的目的.
小结
1、当, , 时代数式的值是( )
A.1 B. 2 C.3 D. 4
A
2、如果,那么=________.
3
基础巩固
3、堤坝的横截面是梯形,测得梯形上底为a=18m,下底b=36m,高h=20m,求这个截面的面积.
a
b
h
解:梯形面积公式为:
将a=18,b=36,h=20代入上面公式,得
答:堤坝的横截面积是540m2
基础巩固
知识
考点
根据问题列代数式,并求代数式的值
代数式的值的求法
课堂总结
空白演示
单击输入您的封面副标题
谢 谢 聆 听
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
