苏科版九年级数学上册 第2章圆小结与思考课件(共24张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 第2章圆小结与思考课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 00:00:00 | ||
图片预览

文档简介
(共24张PPT)
小结与思考
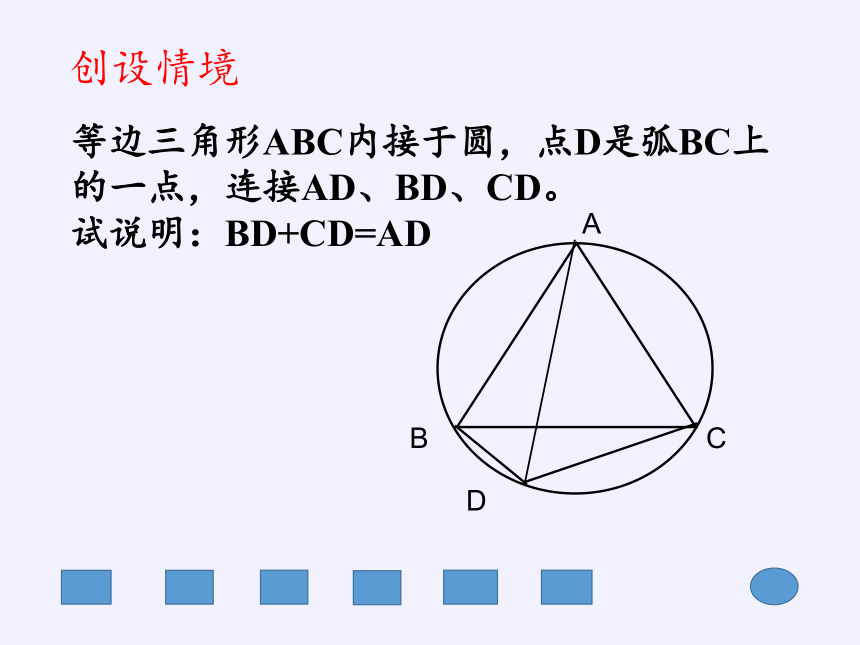
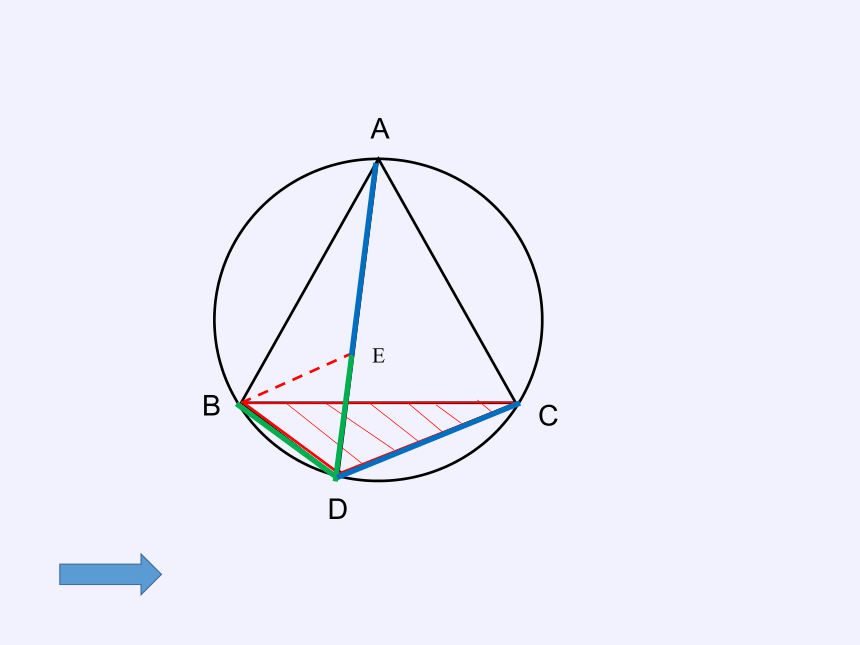
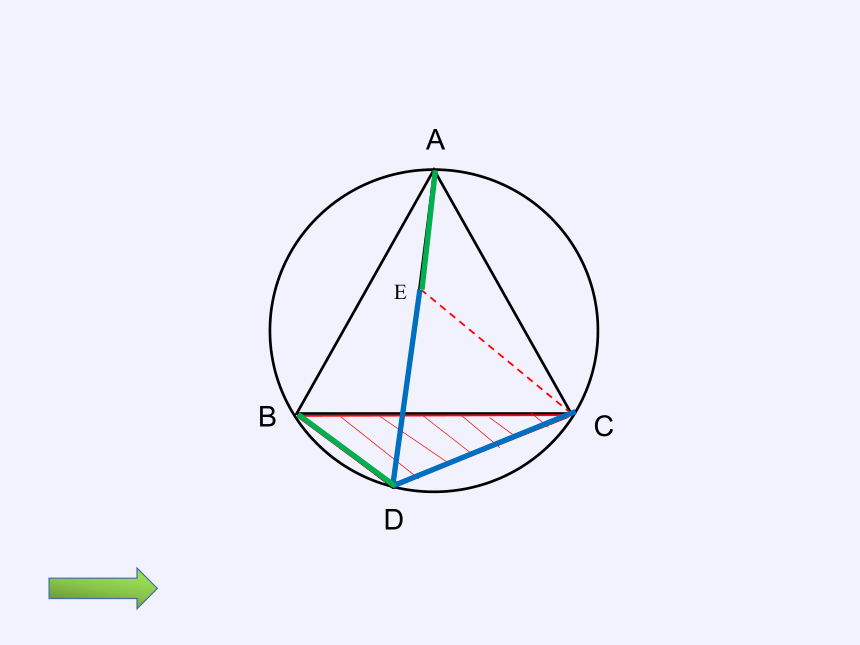
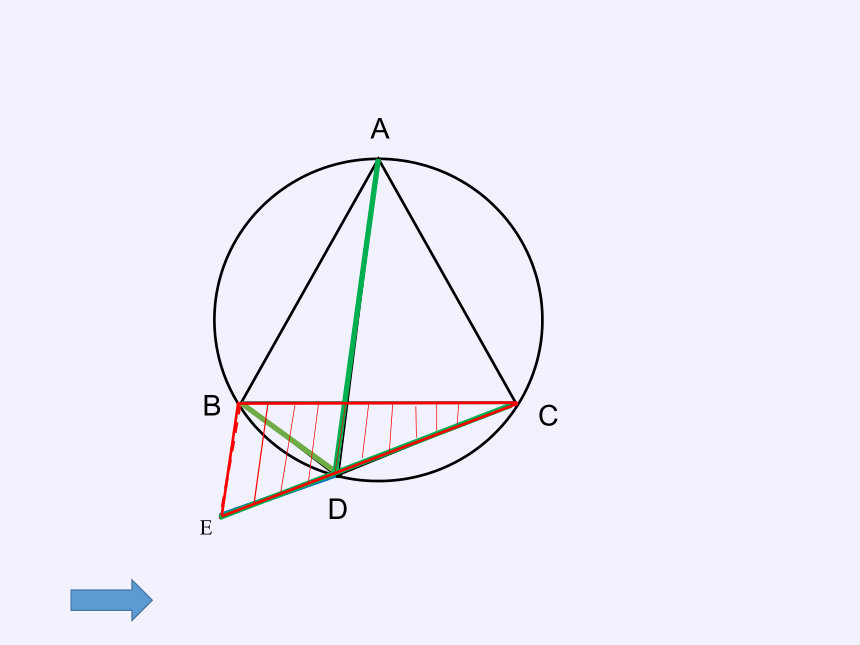
等边三角形ABC内接于圆,点D是弧BC上的一点,连接AD、BD、CD。
试说明:BD+CD=AD
D
C
B
A
创设情境
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
D
C
A
B
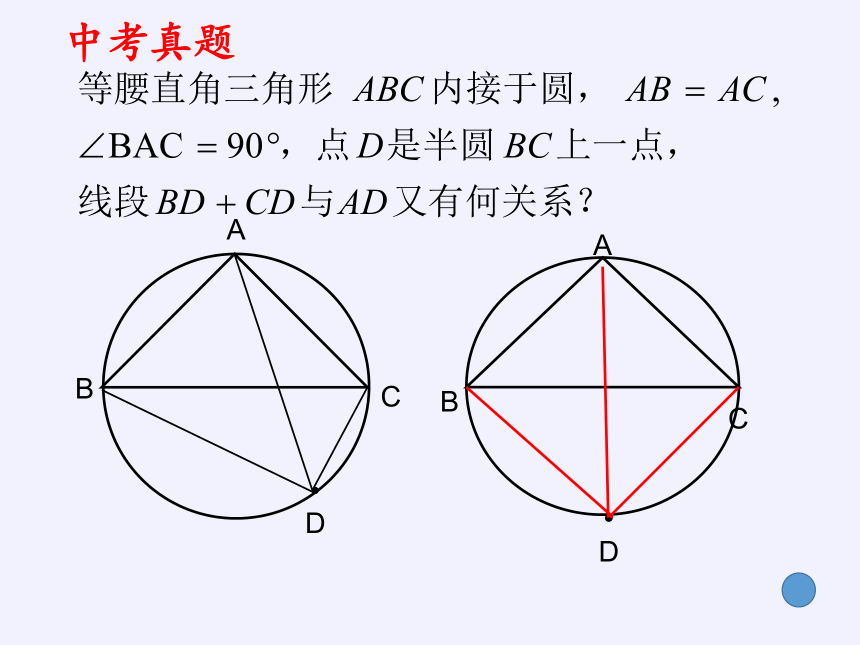
中考真题
A
C
B
D
若点D在弧BC上,猜想:BD+CD与AD有
没有什么数量关系?
延伸探究1
若三角形ABC是等腰三角形,AB=AC
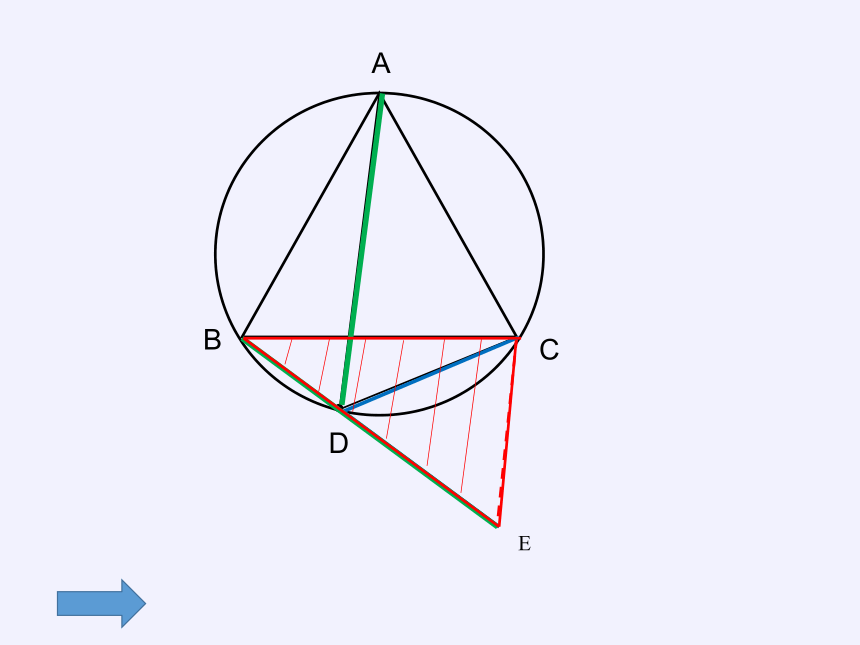
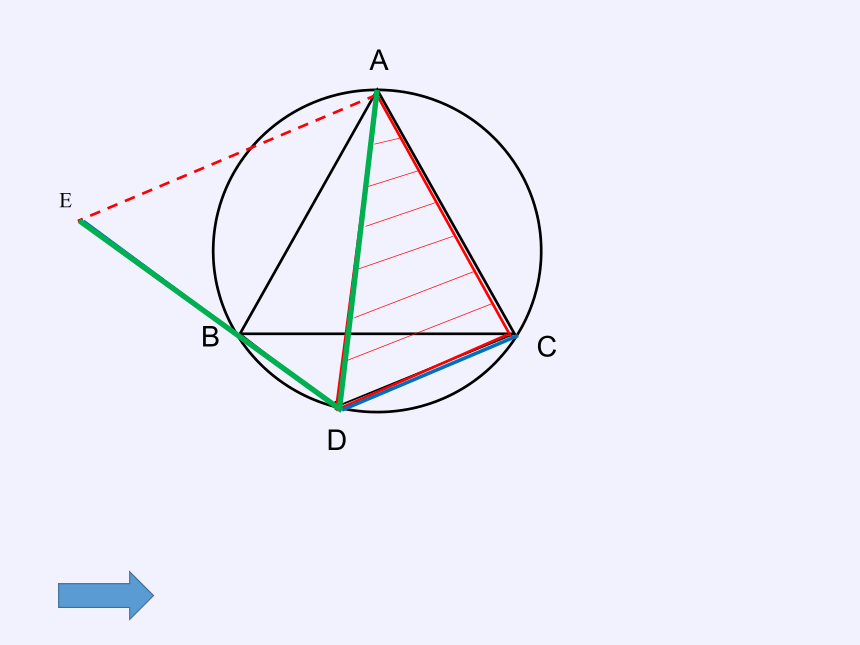
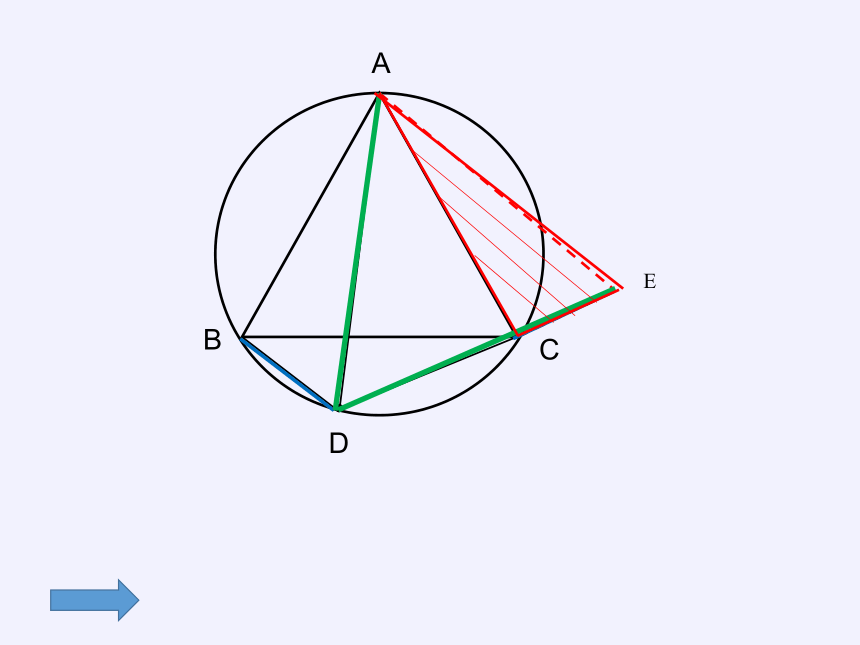
等腰三角形ABC内接于圆,AB=AC,∠ABC=30°,点D是弧BC上的一点,线段BD+CD与AD有没有关系呢?
D
C
A
B
探究应用
探究应用
A
C
B
D
延伸探究2
D
A
C
B
A
C
B
D
延伸探究2
A
C
B
D
E
延伸探究2
A
C
B
D
E
延伸探究2
A
C
B
D
E
延伸探究2
A
C
B
D
若点D在弧AB上,猜想:CD-BD与AD的数量关系又是什么?
延伸探究2
A
C
B
D
若点D在弧AC上,猜想:BD-CD与AD的数量关系又是什么?
延伸探究3
E
探究应用
D
A
C
B
探究应用
A
C
B
D
A
C
B
D
P
正方形ABCD是圆的内接正方形,P是弧BC上的一点,问PA、PB、PC间满足什么数量关系?
探究应用
小结
谈一谈你学到了什么?
谢 谢
小结与思考
等边三角形ABC内接于圆,点D是弧BC上的一点,连接AD、BD、CD。
试说明:BD+CD=AD
D
C
B
A
创设情境
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
D
C
A
B
中考真题
A
C
B
D
若点D在弧BC上,猜想:BD+CD与AD有
没有什么数量关系?
延伸探究1
若三角形ABC是等腰三角形,AB=AC
等腰三角形ABC内接于圆,AB=AC,∠ABC=30°,点D是弧BC上的一点,线段BD+CD与AD有没有关系呢?
D
C
A
B
探究应用
探究应用
A
C
B
D
延伸探究2
D
A
C
B
A
C
B
D
延伸探究2
A
C
B
D
E
延伸探究2
A
C
B
D
E
延伸探究2
A
C
B
D
E
延伸探究2
A
C
B
D
若点D在弧AB上,猜想:CD-BD与AD的数量关系又是什么?
延伸探究2
A
C
B
D
若点D在弧AC上,猜想:BD-CD与AD的数量关系又是什么?
延伸探究3
E
探究应用
D
A
C
B
探究应用
A
C
B
D
A
C
B
D
P
正方形ABCD是圆的内接正方形,P是弧BC上的一点,问PA、PB、PC间满足什么数量关系?
探究应用
小结
谈一谈你学到了什么?
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
