数学人教A版选择性必修第一册第一单元空间向量与立体几何 检测卷 B卷(Word含解析)
文档属性
| 名称 | 数学人教A版选择性必修第一册第一单元空间向量与立体几何 检测卷 B卷(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 974.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 20:42:59 | ||
图片预览




文档简介
选择性必修第一册第一单元达标检测卷
空间向量与立体几何(B)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点关于平面的对称点为( )
A. B. C. D.
2.已知点,,,则的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
3.如图,在平行六面体的棱中,与向量模相等的向量有( )
A.0个 B.3个 C.7个 D.9个
4.已知平面的法向量是,平面的法向量是,若,则的值是( )
A. B. C. D.
5.在正四面体中,,,,为的中点,为的中点,则用表示为( )
A. B.
C. D.
6.如图,在平行六面体中,与的交点为,点在上,且,则下列向量中与相等的向量是( )
A. B.
C. D.
7.在空间直角坐标系中,已知点,点,则( )
A. B. C. D.
8.若直线的一个方向向量,平面的一个法向量为,则( )
A. B.
C. D.A、C都有可能
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.对于任意非零向量,,以下说法错误的有( )
A.若,则
B.若,则
C.
D.若,则为单位向量
10.若,,与的夹角为,则的值为( )
A. B. C. D.
11.如图,棱长为的正方体中,为线段上的动点(不含端点),则下列结论正确的是( )
A.直线与所成的角可能是
B.平面平面
C.三棱锥的体积为定值
D.平面截正方体所得的截面可能是直角三角形
12.如图所示,正方体中,,点在侧面及其边界上运动,并且总是保持,则以下四个结论正确的是( )
A. B.点必在线段上
C. D.平面
三、填空题:本大题共4小题,每小题5分.
13.已知,,则线段的中点坐标为________;_________.
14.在空间直角坐标系中,点和点的距离为,则实数的值为_______.
15.直三棱柱中,若,,,则______.
16.是空间四点,有以下条件:
①;②;
③;④,
能使四点一定共面的条件是______.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,三棱柱中,平面平面,且 ,,,,在①,②,两个条件中选择一个条件,求异面直线与所成角的余弦值.
18.(12分)已知空间中三点,,,设,.
(1)若,且,求向量;
(2)已知向量与互相垂直,求的值;
(3)求的面积.
19.(12分)如图和均为等腰直角三角形,,,平面平面,平面,,.
(1)证明:;
(2)求二面角的余弦值.
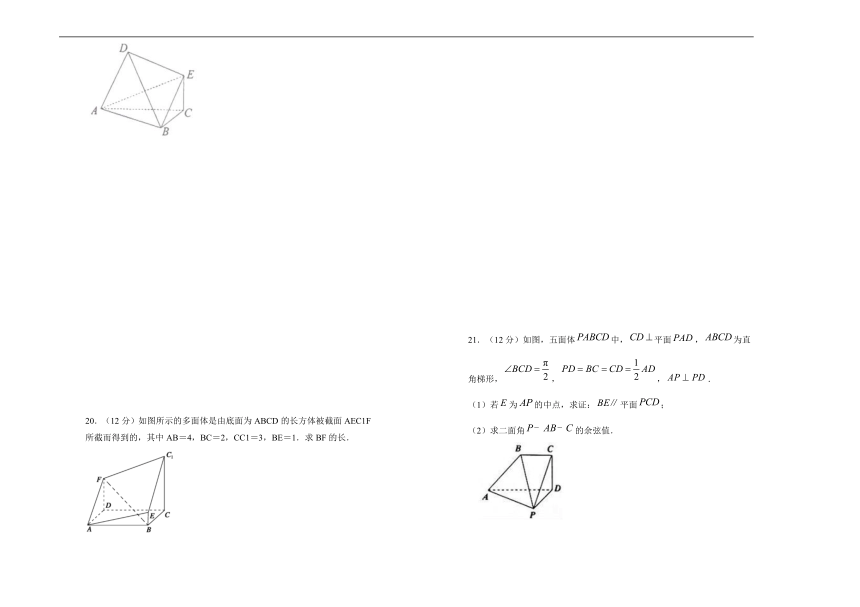
20.(12分)如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,其中AB=4,BC=2,CC1=3,BE=1.求BF的长.
21.(12分)如图,五面体中,平面,为直角梯形,,,.
(1)若为的中点,求证:平面;
(2)求二面角的余弦值.
22.(12分)如图,在长方体中,,,,为的中点,为的中点.
(1)证明:平面;
(2)求平面与平面所成二面角的正弦值.
达标检测卷
空间向量与立体几何(B)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】点关于平面的对称点是坐标不变,变为相反数,
所以点关于平面的对称点为,故选C.
2.【答案】C
【解析】,,
.
所以,故是直角三角形,故选C.
3.【答案】C
【解析】向量模相等即长度相等,根据平行六面体的性质可知,
与向量模相等的向量是,,,,,,,共个,故选C.
4.【答案】C
【解析】由于两个平面垂直,故它们的法向量也垂直,
即,,故选C.
5.【答案】D
【解析】
,
∴,故选D.
6.【答案】C
【解析】因为,所以,
在平行六面体中,
,
故选C.
7.【答案】B
【解析】,,故选B.
8.【答案】B
【解析】直线的一个方向向量为,平面的一个法向量为,
则,,故选B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】BD
【解析】对于A选项,因为,则,A选项正确;
对于B选项,若,且,,若,但分式无意义,B选项错误;
对于C选项,由空间向量数量积的坐标运算可知,C选项正确;
对于D选项,若,则,此时,不是单位向量,D选项错误,
故选BD.
10.【答案】AC
【解析】由已知,
,,
,解得或,
故选AC.
11.【答案】BC
【解析】对于,以为原点,为轴,为轴,为轴,建立空间直角坐标系,
,,,
设,,,
,
,,,
∴直线与所成的角为,故A错误;
对于B,正方体中,,,
∵,∴平面,
∵平面,∴平面平面,故B正确;
对于C,,到平面的距离,
∴三棱锥的体积:为定值,故C正确;
对于D,平面APD1截正方体所得的截面不可能是直角三角形,故D错误,
故选BC.
12.【答案】BD
【解析】对于A,在平面上,平面平面,
到平面即为到平面的距离,即为正方体棱长,
,A错误;
对于B,以为坐标原点可建立如下图所示的空间直角坐标系:
则,,,,,,
,,,
,,,即,
,,即三点共线,
必在线段上,B正确;
对于C,,,,
与不垂直,C错误;
对于D,,,,,,
设平面的法向量,
,令,则,,,
,即,平面,D正确,
故选BD.
三、填空题:本大题共4小题,每小题5分.
13.【答案】、
【解析】设线段的中点坐标为,
由中点坐标公式可得,
即线段的中点坐标为,可得,
故答案为,.
14.【答案】2
【解析】由题意得.
15.【答案】
【解析】如图所示:
因为,,,
所以.
故答案为.
16.【答案】④
【解析】对于④,,
由空间向量共面定理可知四点一定共面,①②③不满足共面定理的条件,
故答案为④.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】见解析.
【解析】若选择条件①,则以为坐标原点,,,所在直线分别为轴、轴、轴,
则,,,,
所以,.
设所求的角为,则,
即异面直线与所成角的余弦值为.
若选择条件②,则以为坐标原点,,所在直线分别为轴、轴,建立如图所示的空间直角坐标系,
则,,,,
所以,.
设所求的角为,则,
即异面直线与所成角的余弦值为.
18.【答案】(1)或;(2);(3).
【解析】(1)空间中三点,,,
设,,
所以,
,
,
,且,设,
,
,,
或.
(2),,
且向量与互相垂直,
,解得,
的值是.
(3)因为,,,
,,,
,
,
.
19.【答案】(1)证明见解析;(2).
【解析】(1)证明:设的中点为,连结,
因为为等腰直角三角形,,,
所以,,
又,所以平面,
因为平面平面,平面平面,
平面,,
所以⊥平面,
又平面,所以.
所以可确定唯一确定的平面,
又平面,.
(2)以为坐标原点,建立如图所示的空间直角坐标系,
则,,,,
,,.
设平面的法向量,
则,即,令,得;
设平面的法向量,
则,即,令,得,
设二面角平面角为,则,
所以二面角的余弦值为.
20.【答案】.
【解析】建立如图所示的空间直角坐标系,
则,,,,,.
设.
∵四边形为平行四边形,∴由,得,
∴,∴,.
于是,即BF的长为.
21.【答案】(1)证明见解析;(2).
【解析】(1)证明:取的中点,连接,
因为分别是的中点,所以且,
因为,,所以且,所以,
又平面平面,所以平面.
(2)以为坐标原点,所在直线分别为轴和轴,建立如图所示的空间直角坐标系,
不妨设,
则,,,,,
,,,
设平面的一个法向量为,则,
令,得,
同理可求平面的一个法向量为,
平面和平面为同一个平面,
所以二面角的余弦值为.
22.【答案】(1)证明见解析;(2).
【解析】(1)证明:如图,
取的中点,连接,.
∵,,且.
∵,,∴,,
∴四边形为平行四边形,∴.
又∵平面,平面,∴平面.
(2)解:以点为原点,向量,,方向分别为,,轴的正方向建立如图所示的空间直角坐标系,
则,,,,,
∴,,,.
设平面的一个法向量为,
则有,解得,取,
得,∴;
设平面的一个法向量为,
则有,解得,取,得,
∴,
由,,,∴,
故平面与平面所成二面角的正弦值为.
空间向量与立体几何(B)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点关于平面的对称点为( )
A. B. C. D.
2.已知点,,,则的形状是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
3.如图,在平行六面体的棱中,与向量模相等的向量有( )
A.0个 B.3个 C.7个 D.9个
4.已知平面的法向量是,平面的法向量是,若,则的值是( )
A. B. C. D.
5.在正四面体中,,,,为的中点,为的中点,则用表示为( )
A. B.
C. D.
6.如图,在平行六面体中,与的交点为,点在上,且,则下列向量中与相等的向量是( )
A. B.
C. D.
7.在空间直角坐标系中,已知点,点,则( )
A. B. C. D.
8.若直线的一个方向向量,平面的一个法向量为,则( )
A. B.
C. D.A、C都有可能
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.对于任意非零向量,,以下说法错误的有( )
A.若,则
B.若,则
C.
D.若,则为单位向量
10.若,,与的夹角为,则的值为( )
A. B. C. D.
11.如图,棱长为的正方体中,为线段上的动点(不含端点),则下列结论正确的是( )
A.直线与所成的角可能是
B.平面平面
C.三棱锥的体积为定值
D.平面截正方体所得的截面可能是直角三角形
12.如图所示,正方体中,,点在侧面及其边界上运动,并且总是保持,则以下四个结论正确的是( )
A. B.点必在线段上
C. D.平面
三、填空题:本大题共4小题,每小题5分.
13.已知,,则线段的中点坐标为________;_________.
14.在空间直角坐标系中,点和点的距离为,则实数的值为_______.
15.直三棱柱中,若,,,则______.
16.是空间四点,有以下条件:
①;②;
③;④,
能使四点一定共面的条件是______.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,三棱柱中,平面平面,且 ,,,,在①,②,两个条件中选择一个条件,求异面直线与所成角的余弦值.
18.(12分)已知空间中三点,,,设,.
(1)若,且,求向量;
(2)已知向量与互相垂直,求的值;
(3)求的面积.
19.(12分)如图和均为等腰直角三角形,,,平面平面,平面,,.
(1)证明:;
(2)求二面角的余弦值.
20.(12分)如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,其中AB=4,BC=2,CC1=3,BE=1.求BF的长.
21.(12分)如图,五面体中,平面,为直角梯形,,,.
(1)若为的中点,求证:平面;
(2)求二面角的余弦值.
22.(12分)如图,在长方体中,,,,为的中点,为的中点.
(1)证明:平面;
(2)求平面与平面所成二面角的正弦值.
达标检测卷
空间向量与立体几何(B)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】点关于平面的对称点是坐标不变,变为相反数,
所以点关于平面的对称点为,故选C.
2.【答案】C
【解析】,,
.
所以,故是直角三角形,故选C.
3.【答案】C
【解析】向量模相等即长度相等,根据平行六面体的性质可知,
与向量模相等的向量是,,,,,,,共个,故选C.
4.【答案】C
【解析】由于两个平面垂直,故它们的法向量也垂直,
即,,故选C.
5.【答案】D
【解析】
,
∴,故选D.
6.【答案】C
【解析】因为,所以,
在平行六面体中,
,
故选C.
7.【答案】B
【解析】,,故选B.
8.【答案】B
【解析】直线的一个方向向量为,平面的一个法向量为,
则,,故选B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】BD
【解析】对于A选项,因为,则,A选项正确;
对于B选项,若,且,,若,但分式无意义,B选项错误;
对于C选项,由空间向量数量积的坐标运算可知,C选项正确;
对于D选项,若,则,此时,不是单位向量,D选项错误,
故选BD.
10.【答案】AC
【解析】由已知,
,,
,解得或,
故选AC.
11.【答案】BC
【解析】对于,以为原点,为轴,为轴,为轴,建立空间直角坐标系,
,,,
设,,,
,
,,,
∴直线与所成的角为,故A错误;
对于B,正方体中,,,
∵,∴平面,
∵平面,∴平面平面,故B正确;
对于C,,到平面的距离,
∴三棱锥的体积:为定值,故C正确;
对于D,平面APD1截正方体所得的截面不可能是直角三角形,故D错误,
故选BC.
12.【答案】BD
【解析】对于A,在平面上,平面平面,
到平面即为到平面的距离,即为正方体棱长,
,A错误;
对于B,以为坐标原点可建立如下图所示的空间直角坐标系:
则,,,,,,
,,,
,,,即,
,,即三点共线,
必在线段上,B正确;
对于C,,,,
与不垂直,C错误;
对于D,,,,,,
设平面的法向量,
,令,则,,,
,即,平面,D正确,
故选BD.
三、填空题:本大题共4小题,每小题5分.
13.【答案】、
【解析】设线段的中点坐标为,
由中点坐标公式可得,
即线段的中点坐标为,可得,
故答案为,.
14.【答案】2
【解析】由题意得.
15.【答案】
【解析】如图所示:
因为,,,
所以.
故答案为.
16.【答案】④
【解析】对于④,,
由空间向量共面定理可知四点一定共面,①②③不满足共面定理的条件,
故答案为④.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】见解析.
【解析】若选择条件①,则以为坐标原点,,,所在直线分别为轴、轴、轴,
则,,,,
所以,.
设所求的角为,则,
即异面直线与所成角的余弦值为.
若选择条件②,则以为坐标原点,,所在直线分别为轴、轴,建立如图所示的空间直角坐标系,
则,,,,
所以,.
设所求的角为,则,
即异面直线与所成角的余弦值为.
18.【答案】(1)或;(2);(3).
【解析】(1)空间中三点,,,
设,,
所以,
,
,
,且,设,
,
,,
或.
(2),,
且向量与互相垂直,
,解得,
的值是.
(3)因为,,,
,,,
,
,
.
19.【答案】(1)证明见解析;(2).
【解析】(1)证明:设的中点为,连结,
因为为等腰直角三角形,,,
所以,,
又,所以平面,
因为平面平面,平面平面,
平面,,
所以⊥平面,
又平面,所以.
所以可确定唯一确定的平面,
又平面,.
(2)以为坐标原点,建立如图所示的空间直角坐标系,
则,,,,
,,.
设平面的法向量,
则,即,令,得;
设平面的法向量,
则,即,令,得,
设二面角平面角为,则,
所以二面角的余弦值为.
20.【答案】.
【解析】建立如图所示的空间直角坐标系,
则,,,,,.
设.
∵四边形为平行四边形,∴由,得,
∴,∴,.
于是,即BF的长为.
21.【答案】(1)证明见解析;(2).
【解析】(1)证明:取的中点,连接,
因为分别是的中点,所以且,
因为,,所以且,所以,
又平面平面,所以平面.
(2)以为坐标原点,所在直线分别为轴和轴,建立如图所示的空间直角坐标系,
不妨设,
则,,,,,
,,,
设平面的一个法向量为,则,
令,得,
同理可求平面的一个法向量为,
平面和平面为同一个平面,
所以二面角的余弦值为.
22.【答案】(1)证明见解析;(2).
【解析】(1)证明:如图,
取的中点,连接,.
∵,,且.
∵,,∴,,
∴四边形为平行四边形,∴.
又∵平面,平面,∴平面.
(2)解:以点为原点,向量,,方向分别为,,轴的正方向建立如图所示的空间直角坐标系,
则,,,,,
∴,,,.
设平面的一个法向量为,
则有,解得,取,
得,∴;
设平面的一个法向量为,
则有,解得,取,得,
∴,
由,,,∴,
故平面与平面所成二面角的正弦值为.
