数学人教A版选择性必修第一册第一单元空间向量与立体几何 检测卷 A卷(Word含解析)
文档属性
| 名称 | 数学人教A版选择性必修第一册第一单元空间向量与立体几何 检测卷 A卷(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 994.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 20:45:36 | ||
图片预览




文档简介
选择性必修第一册第一单元达标检测卷
空间向量与立体几何(A)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在四棱锥中,底面是正方形,为的中点,若,,,则( )
A. B.
C. D.
2.空间四边形中,若向量,,点,分别为线段,的中点,则的坐标为( )
A. B.
C. D.
3.若向量,,,则为( )
A. B. C.或 D.或
4.设,,向量,,,且,,则( )
A. B. C. D.
5.已知平面内有一个点,的一个法向量为,则下列点在平面内的是( )
A. B.
C. D.
6.在三棱柱中,侧棱底面,,点,分别是,的中点,若,则异面直线与所成角的余弦值为( )
A. B. C. D.
7.在棱长为的正方体中,点为的中点,则点到平面的距离为( )
A. B. C. D.
8.如图,在直三棱柱中,,,是的中点,则直线与平面的距离为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.在长方体中,,,,则下列等式成立的是( )
A. B.
C. D.
10.下列命题中不正确的是( )
A.
B.在平行六面体中,
C.若与,与都是共面向量,则与也是共面向量
D.对任意两个非零空间向量,,若存在实数使得,则
11.已知点为三棱锥的底面所在平面内的一点,且(,),则下列说法正确的是( )
A. B.
C.的最大值为 D.的最大值为
12.在棱长为的正方体中,以为原点,以,,分别为轴,轴,轴正方向建立空间直角坐标系,点为线段上一动点,则到平面距离的可能取值为( )
A. B. C. D.
三、填空题:本大题共4小题,每小题5分.
13.设平面,的法向量分别是,,且平面,所成锐二面角的余弦值为,则 .
14.已知,,,若,,三向量共面,则 .
15.已知直线的方向向量为,为直线上一点,若点为直线外一点,则 ,到直线上的距离为 .
16.在菱形中,,,将菱形沿对角线折成直二面角,折起后直线与间的距离为 .
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①,②平面,③三个条件中选两个条件补充在下面的横线处,并加以解答.
如图,在三棱锥中,已知__________,且平面平面.
(1)证明:;
(2)求直线与平面所成角的正弦值.
18.(12分)已知在正方体中,,,分别是,和的中点,利用向量法证明:
(1)平面;
(2)平面平面.
19.(12分)如图,在四棱锥中,底面,底面是正方形,,,分别是,的中点.
(1)求证:;
(2)在平面内求一点,使平面,并证明你的结论.
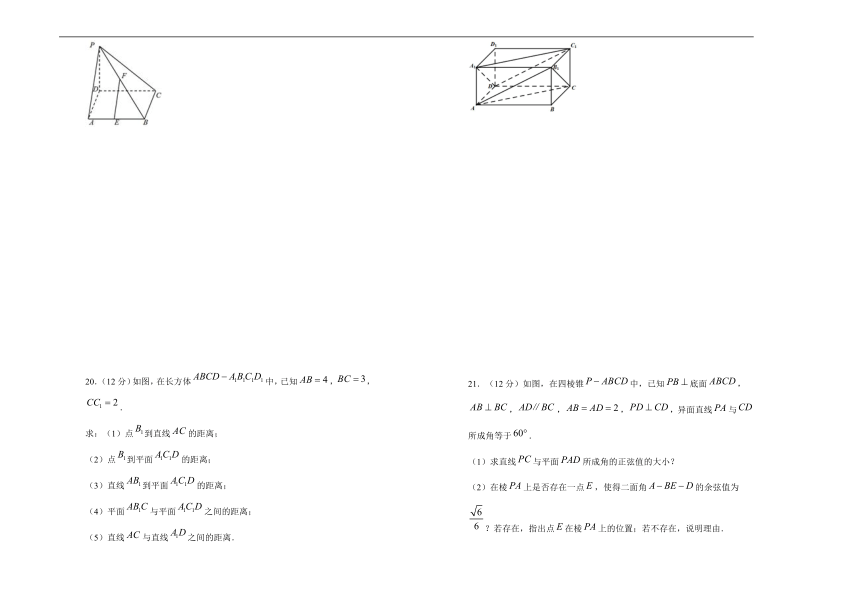
20.(12分)如图,在长方体中,已知,,.
求:(1)点到直线的距离;
(2)点到平面的距离;
(3)直线到平面的距离;
(4)平面与平面之间的距离;
(5)直线与直线之间的距离.
21.(12分)如图,在四棱锥中,已知底面,,,,,异面直线与所成角等于.
(1)求直线与平面所成角的正弦值的大小?
(2)在棱上是否存在一点,使得二面角的余弦值为?若存在,指出点在棱上的位置;若不存在,说明理由.
22.(12分)如图已知是矩形,,分别为边,的中点,与交于点,沿将矩形折起,设,,二面角的大小为.
(1)当时,求的值;
(2)当时,点是线段上一点,直线与平面所成的角为.若,求线段的长.
达标检测卷
空间向量与立体几何(A)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】
.
2.【答案】B
【解析】取中点,连接,,
则,,
从而.
3.【答案】D
【解析】由,化简得,
解得或.
4.【答案】C
【解析】∵,∴,∴,∴,
∵,∴,∴,∴,
∴,∴.
5.【答案】B
【解析】要判断点是否在平面内,
只需要判断向量与平面的法向量是否垂直,即是否为,
因此,要对每个选项进行检验.
对于选项A,,,故排除A;
对于选项B,,则,故B正确;
同理可排除C,D,故选B.
6.【答案】A
【解析】如图,建立空间直角坐标系,设,
则,,,,
,,
所以,
所以异面直线与所成角的余弦值为,故选A.
7.【答案】C
【解析】以为原点建立如图所示的空间直角坐标系,
则,,,∴,,
设平面的一个法向量为,则,∴,
∴,
而,∴,∴点到平面的距离为.
8.【答案】B
【解析】由三角形的中位线可证平面,
而由是直三棱柱,且,
故以为原点,以,,分别为,,轴建立空间直角坐标系,
则,,,,
∴,,
设平面的一个法向量为,则有,
∴,取,得,
又,直线与平面的距离为.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】CD
【解析】,∴C正确;
,∴D正确.
10.【答案】BC
【解析】在平行六面体中,,∴B错误;
在正方体中,若,,,满足与,与都是共面向量,但与不是共面向量,∴C错误,
故选BC.
11.【答案】BC
【解析】根据空间向量基本定理可知,,即,∴B正确;
又由基本不等式可得,当且仅当时等号成立,∴C正确.
12.【答案】AB
【解析】由题意可知,,,,
设,∴,,
设平面的一个法向量为,则,
令,可得,
又,∴到平面距离为,故选AB.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】,所以,
所以.
14.【答案】
【解析】∵与不共线,∴与可取作此平面的一个基向量,
∵,,三向量共面,∴存在实数,使得,
∴,解得,
故答案为.
15.【答案】,
【解析】由已知得,,
∴在上的投影长度为,
∴点到直线的距离为.
16.【答案】
【解析】设,
∵在菱形中,,折起后,,两两垂直,
以为坐标原点,建立如下图的空间直角坐标系.
∵在原菱形中,,,∴,,
∴,,,,∴,,
设,令,则,
令,则,,∴,
又∵,∴与间的距离.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)证明见解析;(2).
【解析】(1)若选②:如图,作于点,
∵平面平面,平面平面,平面,,
∴平面,
又平面,∴,矛盾.
所以②必不选,故选①③.
下面证明:.
作,交的延长线于点,连结.
∵平面平面,平面平面,平面,,
∴平面,
又∵平面,∴,,
在中,……①,
在中,……②,
联立①②可得,,
在中,,
∵,∴,即,
又平面,且,∴平面,
∵平面,∴.
(2)由(1)问可知两两互相垂直,则以为原点,分别为轴建立空间直线坐标系,
,,,,
,,,
设平面的一个法向量为,
则,取,得,
∴,
∴直线与平面所成角的正弦.
18.【答案】(1)证明见解析;(2)证明见解析.
【解析】以为坐标原点,,,分别为,,轴的正方向,
建立空间直角坐标系,并设正方体的棱长为,
则,,,,.
(1)由正方体的性质知平面,
∴为平面的一个法向量,
由于,则又平面,,∴,∴平面.
(2)由于,,,即.
由于平面,∴平面,
又由(1),知平面,,
∴由两个平面平行的判定定理,知平面平面.
19.【答案】(1)证明见解析;(2)点为的中点,证明见解析.
【解析】(1)证明:以,,所在的直线分别为轴,轴,轴建立空间直角坐标系(如图),
设,则,,,,,,∴,,
∴,∴.
(2)∵平面,设,∴.
由(1)知,,
由题意,要使平面,
只需,,
∴,,∴点的坐标为,即点为的中点.
20.【答案】(1);(2);(3);(4);(5).
【解析】以,,所在的直线分别为轴,轴,轴建立如图所示的空间直角坐标系.
由于,,,
则得下列各点的坐标,,,,,,.
(1)过作直线的垂线,垂足为,则.
由前可得,,
设,则,
∵,∴,∴,解得.
∴,
∴.
(2)设平面的一个法向量为,
∵,,∴,即,
令,则得平面的一个法向量为,
又,∴点到平面的距离.
∵平面平面,∴(3)(4)(5)的结论都是.
21.【答案】(1);(2)存在这样的点,为棱上靠近点的三等分点.
【解析】(1)由题以为原点,分别以,,所在的直线为轴,轴,轴,建立空间直角坐标系,设,,
则,,,,,
则,,,
则由可得,即.
又异面直线与所成角等于,则,
设平面的一个法向量为,
,取,则,
又∵,
∴直线与平面所成角的正弦值为.
(2)假设存在这样的点,
设,且,即,,
设平面的一个法向量为,
,得,
又平面的法向量为,,
解得或(不合题意,舍去),
∴存在这样的点,为棱上靠近点的三等分点.
22.【答案】(1);(2).
【解析】(1)设,的中点分别为,,连接,,
建立如图所示的空间直角坐标系,易知,,
∴,,∴.
(2)取得中点,连接,如图,分别以,所在的直线为轴,轴,过作垂直于平面的垂线,为轴,建立如图所示的空间直角坐标系.
由,得,,,,
∴,,,,
设,
则,∴.
设平面的一个法向量为,
∵,∴,取,得,
则是平面的一个法向量,
由题意,得,即,∴或(舍去),
∴.
空间向量与立体几何(A)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在四棱锥中,底面是正方形,为的中点,若,,,则( )
A. B.
C. D.
2.空间四边形中,若向量,,点,分别为线段,的中点,则的坐标为( )
A. B.
C. D.
3.若向量,,,则为( )
A. B. C.或 D.或
4.设,,向量,,,且,,则( )
A. B. C. D.
5.已知平面内有一个点,的一个法向量为,则下列点在平面内的是( )
A. B.
C. D.
6.在三棱柱中,侧棱底面,,点,分别是,的中点,若,则异面直线与所成角的余弦值为( )
A. B. C. D.
7.在棱长为的正方体中,点为的中点,则点到平面的距离为( )
A. B. C. D.
8.如图,在直三棱柱中,,,是的中点,则直线与平面的距离为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.在长方体中,,,,则下列等式成立的是( )
A. B.
C. D.
10.下列命题中不正确的是( )
A.
B.在平行六面体中,
C.若与,与都是共面向量,则与也是共面向量
D.对任意两个非零空间向量,,若存在实数使得,则
11.已知点为三棱锥的底面所在平面内的一点,且(,),则下列说法正确的是( )
A. B.
C.的最大值为 D.的最大值为
12.在棱长为的正方体中,以为原点,以,,分别为轴,轴,轴正方向建立空间直角坐标系,点为线段上一动点,则到平面距离的可能取值为( )
A. B. C. D.
三、填空题:本大题共4小题,每小题5分.
13.设平面,的法向量分别是,,且平面,所成锐二面角的余弦值为,则 .
14.已知,,,若,,三向量共面,则 .
15.已知直线的方向向量为,为直线上一点,若点为直线外一点,则 ,到直线上的距离为 .
16.在菱形中,,,将菱形沿对角线折成直二面角,折起后直线与间的距离为 .
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①,②平面,③三个条件中选两个条件补充在下面的横线处,并加以解答.
如图,在三棱锥中,已知__________,且平面平面.
(1)证明:;
(2)求直线与平面所成角的正弦值.
18.(12分)已知在正方体中,,,分别是,和的中点,利用向量法证明:
(1)平面;
(2)平面平面.
19.(12分)如图,在四棱锥中,底面,底面是正方形,,,分别是,的中点.
(1)求证:;
(2)在平面内求一点,使平面,并证明你的结论.
20.(12分)如图,在长方体中,已知,,.
求:(1)点到直线的距离;
(2)点到平面的距离;
(3)直线到平面的距离;
(4)平面与平面之间的距离;
(5)直线与直线之间的距离.
21.(12分)如图,在四棱锥中,已知底面,,,,,异面直线与所成角等于.
(1)求直线与平面所成角的正弦值的大小?
(2)在棱上是否存在一点,使得二面角的余弦值为?若存在,指出点在棱上的位置;若不存在,说明理由.
22.(12分)如图已知是矩形,,分别为边,的中点,与交于点,沿将矩形折起,设,,二面角的大小为.
(1)当时,求的值;
(2)当时,点是线段上一点,直线与平面所成的角为.若,求线段的长.
达标检测卷
空间向量与立体几何(A)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】
.
2.【答案】B
【解析】取中点,连接,,
则,,
从而.
3.【答案】D
【解析】由,化简得,
解得或.
4.【答案】C
【解析】∵,∴,∴,∴,
∵,∴,∴,∴,
∴,∴.
5.【答案】B
【解析】要判断点是否在平面内,
只需要判断向量与平面的法向量是否垂直,即是否为,
因此,要对每个选项进行检验.
对于选项A,,,故排除A;
对于选项B,,则,故B正确;
同理可排除C,D,故选B.
6.【答案】A
【解析】如图,建立空间直角坐标系,设,
则,,,,
,,
所以,
所以异面直线与所成角的余弦值为,故选A.
7.【答案】C
【解析】以为原点建立如图所示的空间直角坐标系,
则,,,∴,,
设平面的一个法向量为,则,∴,
∴,
而,∴,∴点到平面的距离为.
8.【答案】B
【解析】由三角形的中位线可证平面,
而由是直三棱柱,且,
故以为原点,以,,分别为,,轴建立空间直角坐标系,
则,,,,
∴,,
设平面的一个法向量为,则有,
∴,取,得,
又,直线与平面的距离为.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】CD
【解析】,∴C正确;
,∴D正确.
10.【答案】BC
【解析】在平行六面体中,,∴B错误;
在正方体中,若,,,满足与,与都是共面向量,但与不是共面向量,∴C错误,
故选BC.
11.【答案】BC
【解析】根据空间向量基本定理可知,,即,∴B正确;
又由基本不等式可得,当且仅当时等号成立,∴C正确.
12.【答案】AB
【解析】由题意可知,,,,
设,∴,,
设平面的一个法向量为,则,
令,可得,
又,∴到平面距离为,故选AB.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】,所以,
所以.
14.【答案】
【解析】∵与不共线,∴与可取作此平面的一个基向量,
∵,,三向量共面,∴存在实数,使得,
∴,解得,
故答案为.
15.【答案】,
【解析】由已知得,,
∴在上的投影长度为,
∴点到直线的距离为.
16.【答案】
【解析】设,
∵在菱形中,,折起后,,两两垂直,
以为坐标原点,建立如下图的空间直角坐标系.
∵在原菱形中,,,∴,,
∴,,,,∴,,
设,令,则,
令,则,,∴,
又∵,∴与间的距离.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)证明见解析;(2).
【解析】(1)若选②:如图,作于点,
∵平面平面,平面平面,平面,,
∴平面,
又平面,∴,矛盾.
所以②必不选,故选①③.
下面证明:.
作,交的延长线于点,连结.
∵平面平面,平面平面,平面,,
∴平面,
又∵平面,∴,,
在中,……①,
在中,……②,
联立①②可得,,
在中,,
∵,∴,即,
又平面,且,∴平面,
∵平面,∴.
(2)由(1)问可知两两互相垂直,则以为原点,分别为轴建立空间直线坐标系,
,,,,
,,,
设平面的一个法向量为,
则,取,得,
∴,
∴直线与平面所成角的正弦.
18.【答案】(1)证明见解析;(2)证明见解析.
【解析】以为坐标原点,,,分别为,,轴的正方向,
建立空间直角坐标系,并设正方体的棱长为,
则,,,,.
(1)由正方体的性质知平面,
∴为平面的一个法向量,
由于,则又平面,,∴,∴平面.
(2)由于,,,即.
由于平面,∴平面,
又由(1),知平面,,
∴由两个平面平行的判定定理,知平面平面.
19.【答案】(1)证明见解析;(2)点为的中点,证明见解析.
【解析】(1)证明:以,,所在的直线分别为轴,轴,轴建立空间直角坐标系(如图),
设,则,,,,,,∴,,
∴,∴.
(2)∵平面,设,∴.
由(1)知,,
由题意,要使平面,
只需,,
∴,,∴点的坐标为,即点为的中点.
20.【答案】(1);(2);(3);(4);(5).
【解析】以,,所在的直线分别为轴,轴,轴建立如图所示的空间直角坐标系.
由于,,,
则得下列各点的坐标,,,,,,.
(1)过作直线的垂线,垂足为,则.
由前可得,,
设,则,
∵,∴,∴,解得.
∴,
∴.
(2)设平面的一个法向量为,
∵,,∴,即,
令,则得平面的一个法向量为,
又,∴点到平面的距离.
∵平面平面,∴(3)(4)(5)的结论都是.
21.【答案】(1);(2)存在这样的点,为棱上靠近点的三等分点.
【解析】(1)由题以为原点,分别以,,所在的直线为轴,轴,轴,建立空间直角坐标系,设,,
则,,,,,
则,,,
则由可得,即.
又异面直线与所成角等于,则,
设平面的一个法向量为,
,取,则,
又∵,
∴直线与平面所成角的正弦值为.
(2)假设存在这样的点,
设,且,即,,
设平面的一个法向量为,
,得,
又平面的法向量为,,
解得或(不合题意,舍去),
∴存在这样的点,为棱上靠近点的三等分点.
22.【答案】(1);(2).
【解析】(1)设,的中点分别为,,连接,,
建立如图所示的空间直角坐标系,易知,,
∴,,∴.
(2)取得中点,连接,如图,分别以,所在的直线为轴,轴,过作垂直于平面的垂线,为轴,建立如图所示的空间直角坐标系.
由,得,,,,
∴,,,,
设,
则,∴.
设平面的一个法向量为,
∵,∴,取,得,
则是平面的一个法向量,
由题意,得,即,∴或(舍去),
∴.
