数学人教A版选择性必修第三册第八单元成对数据的统计分析 检测卷 B卷(Word含解析)
文档属性
| 名称 | 数学人教A版选择性必修第三册第八单元成对数据的统计分析 检测卷 B卷(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 763.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 20:54:43 | ||
图片预览




文档简介
选择性必修第三册第八单元达标检测卷
成对数据的统计分析(B)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列语句所表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年 B.名师出高徒
C.吸烟有害健康 D.喜鹊叫喜,乌鸦叫丧
2.在下列各图中,两个变量不具有任何关系的是( )
A.①② B.①③ C.②④ D.④
3.某校一个课外学习小组为研究某作物种子的发芽率和温度(单位:)的关系,在个不同的温度条件下进行种子发芽实验,由实验数据
得到下面的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率和温度的回归方程类型的是( )
A. B.
C. D.
4.根据一位母亲记录儿子岁的身高数据,建立儿子身高 (单位:)对年龄 (单位:岁)的回归直线方程,用此方程预测儿子岁时的身高,有关叙述正确的是( )
A.身高一定为 B.身高大于
C.身高小于 D.身高在左右
5.年是新中国成立周年.年来,在中国共产党的坚强领导下,全国各族人民团结一心,迎难而上,开拓进取,奋力前行,创造了一个又一个人类发展史上的伟大奇迹,中华民族迎来了从站起来、富起来到强起来的伟大飞跃.某公司统计了第年(年是第一年)的经济效益为(千万元),得到如下表格:
若由表中数据得到关于的线性回归方程是,则可预测年经济效益大约是( )
A.千万元 B.千万元 C.千万元 D.千万元
6.通过随机询问名性别不同的高二学生是否爱吃零食,得到如下的列联表:
其中,则下列结论正确的是( )
A.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别有关”
B.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别无关”
C.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别有关”
D.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别无关”
7.随机调查某校名学生是否喜欢跳舞,由列联表和公式计算出,并由此作出结论:“有的可能性认为学生喜欢跳舞与性别有关”,则可以为( )
A. B. C. D.
8.为考察某种药物预防疾病的效果,对只某种动物进行试验,得到如下的列联表:
经计算,统计量的观测值,则认为药物有效出错的可能性不超过( )
已知独立性检验中统计量的临界值参考值为:
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:月日本地降水概率为,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程中,当解释变量每增加个单位时,预报变量多增加个单位
10.下列说法正确的是( )
A.回归直线一定经过样本点的中心
B.若两个具有线性相关关系的变量的相关性越强,则线性相关系数的值越接近于
C.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D.在线性回归模型中,相关指数越接近于,说明回归的效果越好
11.某校计划在课外活动中新增攀岩项目,为了解学生喜欢攀岩和性别是否有关,面向学生开展了一次随机调查,其中参加调查的男女生人数相同,并绘制如图等高条形图,则( )
参考公式:,.
A.参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多
B.参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数多
C.若参与调查的男女生人数均为人,则有的把握认为喜欢攀岩和性别有关
D.无论参与调查的男女生人数为多少,都有的把握认为喜欢攀岩和性别有关
12.下列命题正确的是( )
A.随机变量,且,则
B.已知函数是定义在上的偶函数,且在上单调递减,,则不等式的解集为
C.已知,则“”是“”的充分不必要条件
D.根据一组样本数据的散点图判断出两个变量线性相关,由最小二乘法求得其回归直线方程为,若样本中心点为,则
三、填空题:本大题共4小题,每小题5分.
13.已知回归直线斜率的估计值为,样本点的中心为点,则回归直线的方程为________.
14.某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 不喜欢甜品 合计
南方学生
北方学生
合计
根据表中数据,问是否有的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”______.(填有或没有)
附:
15.在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁,为了考察某种埃博拉病毒疫苗的效果,现随机抽取只小鼠进行试验,得到如下列联表:
参照附表,在犯错误的概率最多不超过_____(填百分比)的前提下,可认为“该种疫苗有预防埃博拉病毒感染的效果”.
参考公式:.
16.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月号到号每天打篮球时间(单位:小时)与当天投篮命中率之间的关系:
小李这天的平均投篮命中率为______;用线性回归分析的方法,预测小李该月号打小时篮球的投篮命中率为_______.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①,②,③这三个条件中,任选一个补充在下面的问题中,并加以解答.
为考查某种药物预防疾病的效果,随机抽查了只服用药的动物和只未服用药的动物得知服用药的动物中患病的比例是,未服用药的动物中患病的比例为___.
(1)根据以上数据完成下列列联表:
(2)能否有的把握认为药物有效 并说明理由.
附:临界值表
参考公式:,.
18.(12分)为加强环境保护,治理空气污染,环境检测部门对某市空气质量进行调研,随机抽查了天空气中的和浓度(单位:),得下表:
(1)估计事件“该市一天空气中浓度不超过,且浓度不超过”的概率;
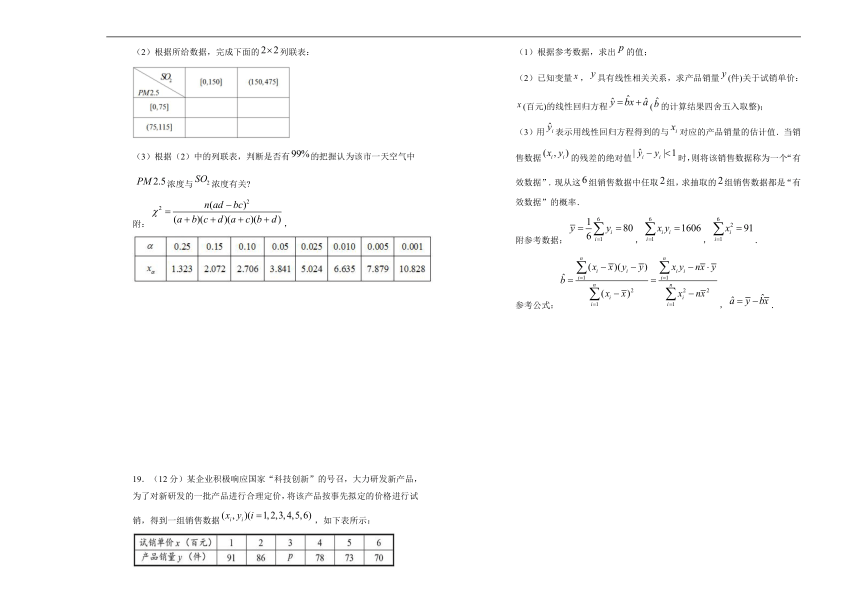
(2)根据所给数据,完成下面的列联表:
(3)根据(2)中的列联表,判断是否有的把握认为该市一天空气中浓度与浓度有关
附:,
19.(12分)某企业积极响应国家“科技创新”的号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据,如下表所示:
(1)根据参考数据,求出的值;
(2)已知变量,具有线性相关关系,求产品销量(件)关于试销单价:(百元)的线性回归方程(的计算结果四舍五入取整);
(3)用表示用线性回归方程得到的与对应的产品销量的估计值.当销售数据的残差的绝对值时,则将该销售数据称为一个“有效数据”.现从这组销售数据中任取组,求抽取的组销售数据都是“有效数据”的概率.
附参考数据:,,.
参考公式:,.
20.(12分)某工厂生产某种型号的农机具零配件,为了预测今年月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度月份至月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价(单位:元)和销售量(单位:千件)之间的组数据如下表所示:
(1)根据至月份的数据,求关于的线性回归方程(系数精确到);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件元,那么工厂如何制定月份的销售单价,才能使该月利润达到最大 (计算结果精确到)
参考公式:回归直线方程,,
参考数据:,.
21.(12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加,为调查该地区某种野生动物的数量,将其分成面积相近的个地块,从这些地块中用简单随机抽样的方法抽取个作为样区,调查得到样本数据,其中和分别表示第个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,,
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本的相关系数(精确到);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大,为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数:,.
22.(12分)年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取名学生对线上教育进行调查,其中男生与女生的人数之比为,其中男生人对于线上教育满意,女生中有名表示对线上教育不满意.
(1)完成列联表,并回答能否有的把握认为对“线上教育是否满意与性别有关”;
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取名学生,再在名学生中抽取名学生,作线上学习的经验介绍,其中抽取男生的个数为,求出的分布列及期望值.
参考公式:附:
达标检测卷
成对数据的统计分析(B)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】D
【解析】瑞雪兆丰年和名师出高徒是根据多年经验总结归纳出来的,吸烟有害健康具有科学根据,所以它们都是相关关系,所以A、B、C三项具有相关关系;
结合生活经验知喜鹊和乌鸦发出叫声是它们自身的生理反应,与人无任何关系,不具有相关关系.
2.【答案】D
【解析】①具有函数关系;②③具有相关关系;④无关系.
3.【答案】D
【解析】由图象可知作为发芽率和温度的回归方程类型最适宜.
4.【答案】D
【解析】用回归直线方程预测的不是准确值,而是估计值.
当时,,只能说身高在左右.
5.【答案】A
【解析】由表格中的数据求得,,
所以样本点的中心坐标为,代入,
得,解得,
∴线性回归方程为,
取,得年经济效益大约是千万元,故选A.
6.【答案】A
【解析】由题意得,
又因为,
所以犯错误的概率不超过的前提下,认为“是否爱吃零食与性别有关”,
故选A.
7.【答案】D
【解析】有的可能性认为学生喜欢跳舞与性别有关,所以.
8.【答案】B
【解析】根据题意,得,
参照附表,可得认为药物有效出错的可能性不超过,故选B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】CD
【解析】对A项,在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越好,故A错误;
对B项,概率只说明事件发生的可能性,某次事件不一定发生,所以并不能说明天气预报不科学,故B错误;
对C项,回归分析模型中,残差平方和越小,说明模型的拟合效果越好,故C正确;
对D项,在回归直线方程中,当解释变量每增加个单位时,预报变量多增加个单位,故D正确.
10.【答案】ACD
【解析】对于选项A,因为回归直线恒过样本点的中心,不一定经过每个样本点,故选项A正确;
对于选项B,由相关系数的绝对值越接近于,相关性越强可知,若两个变量负相关,其相关性越强,则线性相关系数的值越接近于,故选项B错误;
对于选项C,因为在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高,故选项C正确;
对于选项D,因为在线性回归模型中,相关指数越接近于,说明线性回归模型的拟合效果越好,故选项D正确.
11.【答案】AC
【解析】由于参与调查的男生人数和女生人数相同,直接根据等高条形图可知A正确,B错误;
假设男生女生调查的人数均为,根据题意可得:
男生 女生 总计
喜欢
不喜欢
总计
则,
当时,,故C正确;
由于与有关,故D错误.
12.【答案】BD
【解析】由于,则,
则,故A错误;
由于,则,解得,故B正确;
当时,不成立,反之不等式,可以推出,故C错误;
由于,解得,故D正确.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】设回归直线方程为,
又经过点,故,.
14.【答案】有
【解析】根据表中数据,计算观测值,
对照临界值知,有的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”.
15.【答案】
【解析】由题意,计算观测值,
参照附表,可得:在犯错误的概率不超过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”.
16.【答案】;
【解析】平均命中率;
而,,
于是,∴,
令,得.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)列联表见解析;(2)见解析.
【解析】选条件①:
(1)由已知数据可得列联表如下:
(2)由(1)中列联表的数据可得,
因为,故不能够有的把握认为药物有效.
选条件②:
(1)由已知数据可得列联表如下:
患病 未患病 总计
服用药
没服用药
总计
(2)由(1)中列联表的数据可得,
因为,故能够有的把握认为药物有效.
选条件③:
(1)由已知数据可得列联表如下:
患病 未患病 总计
服用药
没服用药
总计
(2)由(1)中列联表的数据可得,
因为,故能够有的把握认为药物有效.
18.【答案】(1);(2)列联表见解析;(3)有的把握认为的浓度与浓度有关.
【解析】(1)由表格可得浓度不超过且浓度不超过的天数有天,
∴概率为.
(2)
(3),
∴有的把握认为的浓度与浓度有关.
19.【答案】(1);(2);(3).
【解析】(1)由,得,求得.
(2)∵,
而,,,
∴,根据取整有,
∴,
∴所求的线性回归方程为.
(3)当时,;当时,;当时,;当时,;当时,;当时,.
满足条件的“有效数据”有、、、共个,
从个销售数据中任意抽取个的所有可能结果有种,抽取的组销售数据都是“有效数据”的有种,
∴抽取的组销售数据都是“有效数据”的概率为.
20.【答案】(1);(2)故月份销售单价为元时,该月利润才能达到最大.
【解析】(1)由条件知,,
,
所以
,
,
故关于的线性回归方程为.
(2)假设月份的销售单价为元,
则由(1)可知,月份零配件销量为,
故月份的利润,
其对称轴,
故月份销售单价为元时,该月利润才能达到最大.
21.【答案】(1)12000;(2);(3)详见解析.
【解析】(1)由题意可知,个样区这种野生动物数量的平均数,
故这种野生动物数量的估计值.
(2)由参考公式得.
(3)由题意可知,各地块间植物覆盖面积差异很大,因此在调查时,先确定该地区各地块间植物覆盖面积大小并且由小到大排序,每十个分为一组,采用系统抽样的方法抽取个地块作为样区进行样本统计.
22.【答案】(1)列联表见解析,有的把握认为;(2)分布列见解析;.
【解析】(1)因为男生人数为,所以女生人数为,
于是可完成列联表,如下:
根据列联表中的数据,得到的观测值,
所以有的把握认为对“线上教育是否满意与性别有关”.
(2)由(1)可知男生抽人,女生抽人,依题可知的可能取值为,
并且服从超几何分布,,
即,,,,
可得分布列为
可得.
成对数据的统计分析(B)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列语句所表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年 B.名师出高徒
C.吸烟有害健康 D.喜鹊叫喜,乌鸦叫丧
2.在下列各图中,两个变量不具有任何关系的是( )
A.①② B.①③ C.②④ D.④
3.某校一个课外学习小组为研究某作物种子的发芽率和温度(单位:)的关系,在个不同的温度条件下进行种子发芽实验,由实验数据
得到下面的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率和温度的回归方程类型的是( )
A. B.
C. D.
4.根据一位母亲记录儿子岁的身高数据,建立儿子身高 (单位:)对年龄 (单位:岁)的回归直线方程,用此方程预测儿子岁时的身高,有关叙述正确的是( )
A.身高一定为 B.身高大于
C.身高小于 D.身高在左右
5.年是新中国成立周年.年来,在中国共产党的坚强领导下,全国各族人民团结一心,迎难而上,开拓进取,奋力前行,创造了一个又一个人类发展史上的伟大奇迹,中华民族迎来了从站起来、富起来到强起来的伟大飞跃.某公司统计了第年(年是第一年)的经济效益为(千万元),得到如下表格:
若由表中数据得到关于的线性回归方程是,则可预测年经济效益大约是( )
A.千万元 B.千万元 C.千万元 D.千万元
6.通过随机询问名性别不同的高二学生是否爱吃零食,得到如下的列联表:
其中,则下列结论正确的是( )
A.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别有关”
B.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别无关”
C.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别有关”
D.在犯错误的概率不超过的前提下,认为“是否爱吃零食与性别无关”
7.随机调查某校名学生是否喜欢跳舞,由列联表和公式计算出,并由此作出结论:“有的可能性认为学生喜欢跳舞与性别有关”,则可以为( )
A. B. C. D.
8.为考察某种药物预防疾病的效果,对只某种动物进行试验,得到如下的列联表:
经计算,统计量的观测值,则认为药物有效出错的可能性不超过( )
已知独立性检验中统计量的临界值参考值为:
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:月日本地降水概率为,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程中,当解释变量每增加个单位时,预报变量多增加个单位
10.下列说法正确的是( )
A.回归直线一定经过样本点的中心
B.若两个具有线性相关关系的变量的相关性越强,则线性相关系数的值越接近于
C.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D.在线性回归模型中,相关指数越接近于,说明回归的效果越好
11.某校计划在课外活动中新增攀岩项目,为了解学生喜欢攀岩和性别是否有关,面向学生开展了一次随机调查,其中参加调查的男女生人数相同,并绘制如图等高条形图,则( )
参考公式:,.
A.参与调查的学生中喜欢攀岩的男生人数比喜欢攀岩的女生人数多
B.参与调查的女生中喜欢攀岩的人数比不喜欢攀岩的人数多
C.若参与调查的男女生人数均为人,则有的把握认为喜欢攀岩和性别有关
D.无论参与调查的男女生人数为多少,都有的把握认为喜欢攀岩和性别有关
12.下列命题正确的是( )
A.随机变量,且,则
B.已知函数是定义在上的偶函数,且在上单调递减,,则不等式的解集为
C.已知,则“”是“”的充分不必要条件
D.根据一组样本数据的散点图判断出两个变量线性相关,由最小二乘法求得其回归直线方程为,若样本中心点为,则
三、填空题:本大题共4小题,每小题5分.
13.已知回归直线斜率的估计值为,样本点的中心为点,则回归直线的方程为________.
14.某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 不喜欢甜品 合计
南方学生
北方学生
合计
根据表中数据,问是否有的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”______.(填有或没有)
附:
15.在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁,为了考察某种埃博拉病毒疫苗的效果,现随机抽取只小鼠进行试验,得到如下列联表:
参照附表,在犯错误的概率最多不超过_____(填百分比)的前提下,可认为“该种疫苗有预防埃博拉病毒感染的效果”.
参考公式:.
16.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月号到号每天打篮球时间(单位:小时)与当天投篮命中率之间的关系:
小李这天的平均投篮命中率为______;用线性回归分析的方法,预测小李该月号打小时篮球的投篮命中率为_______.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①,②,③这三个条件中,任选一个补充在下面的问题中,并加以解答.
为考查某种药物预防疾病的效果,随机抽查了只服用药的动物和只未服用药的动物得知服用药的动物中患病的比例是,未服用药的动物中患病的比例为___.
(1)根据以上数据完成下列列联表:
(2)能否有的把握认为药物有效 并说明理由.
附:临界值表
参考公式:,.
18.(12分)为加强环境保护,治理空气污染,环境检测部门对某市空气质量进行调研,随机抽查了天空气中的和浓度(单位:),得下表:
(1)估计事件“该市一天空气中浓度不超过,且浓度不超过”的概率;
(2)根据所给数据,完成下面的列联表:
(3)根据(2)中的列联表,判断是否有的把握认为该市一天空气中浓度与浓度有关
附:,
19.(12分)某企业积极响应国家“科技创新”的号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据,如下表所示:
(1)根据参考数据,求出的值;
(2)已知变量,具有线性相关关系,求产品销量(件)关于试销单价:(百元)的线性回归方程(的计算结果四舍五入取整);
(3)用表示用线性回归方程得到的与对应的产品销量的估计值.当销售数据的残差的绝对值时,则将该销售数据称为一个“有效数据”.现从这组销售数据中任取组,求抽取的组销售数据都是“有效数据”的概率.
附参考数据:,,.
参考公式:,.
20.(12分)某工厂生产某种型号的农机具零配件,为了预测今年月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度月份至月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价(单位:元)和销售量(单位:千件)之间的组数据如下表所示:
(1)根据至月份的数据,求关于的线性回归方程(系数精确到);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件元,那么工厂如何制定月份的销售单价,才能使该月利润达到最大 (计算结果精确到)
参考公式:回归直线方程,,
参考数据:,.
21.(12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加,为调查该地区某种野生动物的数量,将其分成面积相近的个地块,从这些地块中用简单随机抽样的方法抽取个作为样区,调查得到样本数据,其中和分别表示第个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,,
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本的相关系数(精确到);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大,为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数:,.
22.(12分)年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取名学生对线上教育进行调查,其中男生与女生的人数之比为,其中男生人对于线上教育满意,女生中有名表示对线上教育不满意.
(1)完成列联表,并回答能否有的把握认为对“线上教育是否满意与性别有关”;
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取名学生,再在名学生中抽取名学生,作线上学习的经验介绍,其中抽取男生的个数为,求出的分布列及期望值.
参考公式:附:
达标检测卷
成对数据的统计分析(B)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】D
【解析】瑞雪兆丰年和名师出高徒是根据多年经验总结归纳出来的,吸烟有害健康具有科学根据,所以它们都是相关关系,所以A、B、C三项具有相关关系;
结合生活经验知喜鹊和乌鸦发出叫声是它们自身的生理反应,与人无任何关系,不具有相关关系.
2.【答案】D
【解析】①具有函数关系;②③具有相关关系;④无关系.
3.【答案】D
【解析】由图象可知作为发芽率和温度的回归方程类型最适宜.
4.【答案】D
【解析】用回归直线方程预测的不是准确值,而是估计值.
当时,,只能说身高在左右.
5.【答案】A
【解析】由表格中的数据求得,,
所以样本点的中心坐标为,代入,
得,解得,
∴线性回归方程为,
取,得年经济效益大约是千万元,故选A.
6.【答案】A
【解析】由题意得,
又因为,
所以犯错误的概率不超过的前提下,认为“是否爱吃零食与性别有关”,
故选A.
7.【答案】D
【解析】有的可能性认为学生喜欢跳舞与性别有关,所以.
8.【答案】B
【解析】根据题意,得,
参照附表,可得认为药物有效出错的可能性不超过,故选B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】CD
【解析】对A项,在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越好,故A错误;
对B项,概率只说明事件发生的可能性,某次事件不一定发生,所以并不能说明天气预报不科学,故B错误;
对C项,回归分析模型中,残差平方和越小,说明模型的拟合效果越好,故C正确;
对D项,在回归直线方程中,当解释变量每增加个单位时,预报变量多增加个单位,故D正确.
10.【答案】ACD
【解析】对于选项A,因为回归直线恒过样本点的中心,不一定经过每个样本点,故选项A正确;
对于选项B,由相关系数的绝对值越接近于,相关性越强可知,若两个变量负相关,其相关性越强,则线性相关系数的值越接近于,故选项B错误;
对于选项C,因为在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高,故选项C正确;
对于选项D,因为在线性回归模型中,相关指数越接近于,说明线性回归模型的拟合效果越好,故选项D正确.
11.【答案】AC
【解析】由于参与调查的男生人数和女生人数相同,直接根据等高条形图可知A正确,B错误;
假设男生女生调查的人数均为,根据题意可得:
男生 女生 总计
喜欢
不喜欢
总计
则,
当时,,故C正确;
由于与有关,故D错误.
12.【答案】BD
【解析】由于,则,
则,故A错误;
由于,则,解得,故B正确;
当时,不成立,反之不等式,可以推出,故C错误;
由于,解得,故D正确.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】设回归直线方程为,
又经过点,故,.
14.【答案】有
【解析】根据表中数据,计算观测值,
对照临界值知,有的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”.
15.【答案】
【解析】由题意,计算观测值,
参照附表,可得:在犯错误的概率不超过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”.
16.【答案】;
【解析】平均命中率;
而,,
于是,∴,
令,得.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)列联表见解析;(2)见解析.
【解析】选条件①:
(1)由已知数据可得列联表如下:
(2)由(1)中列联表的数据可得,
因为,故不能够有的把握认为药物有效.
选条件②:
(1)由已知数据可得列联表如下:
患病 未患病 总计
服用药
没服用药
总计
(2)由(1)中列联表的数据可得,
因为,故能够有的把握认为药物有效.
选条件③:
(1)由已知数据可得列联表如下:
患病 未患病 总计
服用药
没服用药
总计
(2)由(1)中列联表的数据可得,
因为,故能够有的把握认为药物有效.
18.【答案】(1);(2)列联表见解析;(3)有的把握认为的浓度与浓度有关.
【解析】(1)由表格可得浓度不超过且浓度不超过的天数有天,
∴概率为.
(2)
(3),
∴有的把握认为的浓度与浓度有关.
19.【答案】(1);(2);(3).
【解析】(1)由,得,求得.
(2)∵,
而,,,
∴,根据取整有,
∴,
∴所求的线性回归方程为.
(3)当时,;当时,;当时,;当时,;当时,;当时,.
满足条件的“有效数据”有、、、共个,
从个销售数据中任意抽取个的所有可能结果有种,抽取的组销售数据都是“有效数据”的有种,
∴抽取的组销售数据都是“有效数据”的概率为.
20.【答案】(1);(2)故月份销售单价为元时,该月利润才能达到最大.
【解析】(1)由条件知,,
,
所以
,
,
故关于的线性回归方程为.
(2)假设月份的销售单价为元,
则由(1)可知,月份零配件销量为,
故月份的利润,
其对称轴,
故月份销售单价为元时,该月利润才能达到最大.
21.【答案】(1)12000;(2);(3)详见解析.
【解析】(1)由题意可知,个样区这种野生动物数量的平均数,
故这种野生动物数量的估计值.
(2)由参考公式得.
(3)由题意可知,各地块间植物覆盖面积差异很大,因此在调查时,先确定该地区各地块间植物覆盖面积大小并且由小到大排序,每十个分为一组,采用系统抽样的方法抽取个地块作为样区进行样本统计.
22.【答案】(1)列联表见解析,有的把握认为;(2)分布列见解析;.
【解析】(1)因为男生人数为,所以女生人数为,
于是可完成列联表,如下:
根据列联表中的数据,得到的观测值,
所以有的把握认为对“线上教育是否满意与性别有关”.
(2)由(1)可知男生抽人,女生抽人,依题可知的可能取值为,
并且服从超几何分布,,
即,,,,
可得分布列为
可得.
