数学人教A版选择性必修第三册第八单元成对数据的统计分析 检测卷 A卷(Word含解析)
文档属性
| 名称 | 数学人教A版选择性必修第三册第八单元成对数据的统计分析 检测卷 A卷(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 948.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 20:54:17 | ||
图片预览




文档简介
选择性必修第三册第八单元达标检测卷
成对数据的统计分析(A)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.观察下列关于两个变量和的三个散点图,它们从左到右的对应关系依次为( )
A.正相关、负相关、不相关 B.负相关、不相关、正相关
C.负相关、正相关、不相关 D.正相关、不相关、负相关
2.对具有相关关系的两个变量,,收集了组数据:,,,,根据最小二乘法得到线性回归方程,则下列说法一定正确的是( )
A.,都有
B.,使得
C.,都有
D.,使得
3.为考察、两种药物预防某疾病的效果,进行动物试验,分别得到如下等高条形图,根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物、对该疾病均没有预防效果
B.药物、对该疾病均有显著的预防效
C.药物的预防效果优于药物的预防效果
D.药物的预防效果优于药物的预防效果
4.已知一组数据,,,的线性回归方程为,则的值为( )
A. B. C. D.
5.某校学生会为研究该校学生的性别与语文,数学、英语成绩这个变量之间的关系,随机抽查了名学生,得到某次期末考试的成绩数据如表至表,根据表中数据可知该校学生语文、数学、英语这三门学科中( )
表
表
表
A.语文成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
B.数学成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
C.英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
D.英语成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
6.某研究机构在对具有线性相关的两个变量和进行统计分析时,得到如下数据.
由表中数据求得关于的回归方程为,则在这些样本点中任取一点,该点落在回归直线上方的概率为( )
A. B. C. D.
7.下列说法正确的个数是( )
①分类变量与的随机变量越大,说明“与有关系”的可信度越大
②以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,的值分别是和
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为中,,,,则
A. B. C. D.
8.下图是相关变量的散点图,现对这两个变量进行线性相关分析.
方案一:根据图中所有数据,得到线性回归方程,相关系数为;
方案二:剔除点,根据剩下数据得到线性回归直线方程,相关系数为.则( )
A. B.
C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列命题中,正确的命题有( )
A.用相关指数来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于,说明模型的拟合效果越好
B.若分类变量和的随机变量的观测值越大,则“与相关”的可信程度越小
C残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适
D两个模型中残差平方和越小的模型拟合的效果越好
10.己知某产品的销售额与广告费用之间的关系如下表:
若根据表中的数据用最小二乘法求得对的回归直线方程为,则下列说法中正确的是( )
A.的值是
B.该回归直线过点
C.产品的销售额与广告费用成正相关
D.当广告费用为万元时,销售额一定为万元
11.某公司为了增加其商品的销售利润,调查了该商品投入的广告费用与销售利润的统计数据如下表:
由表中数据,得线性回归方程,,则下列结论正确的是( )
A. B.
C直线过点 D.直线过点
12.下列说法正确的是( )
A.某中学高一年级560人,高二年级540人,高三年级520人,用分层抽样的方法抽取容量为81的样本,则在高一、高二、高三三个年级抽取的人数分别为28、27、26
B.正态分布在区间和上取值的概率相等
C.若两个随机变量的线性相关性越强,则相关系数的值越接近于1
D.若一组数据、、、的众数是,则这组数据的中位数是
三、填空题:本大题共4小题,每小题5分.
13.为了研究某班学生的脚长(单位:厘米)和身高(单位:厘米)的关系,从该班随机抽取名学生,根据测量数据的散点图可以看出与之间有线性相关关系,设其回归直线方程为,已知,,.该班某学生的脚长为,据此估计其身高为_______.
14.有两个分类变量与,其一组观测值如下面的列联表所示:
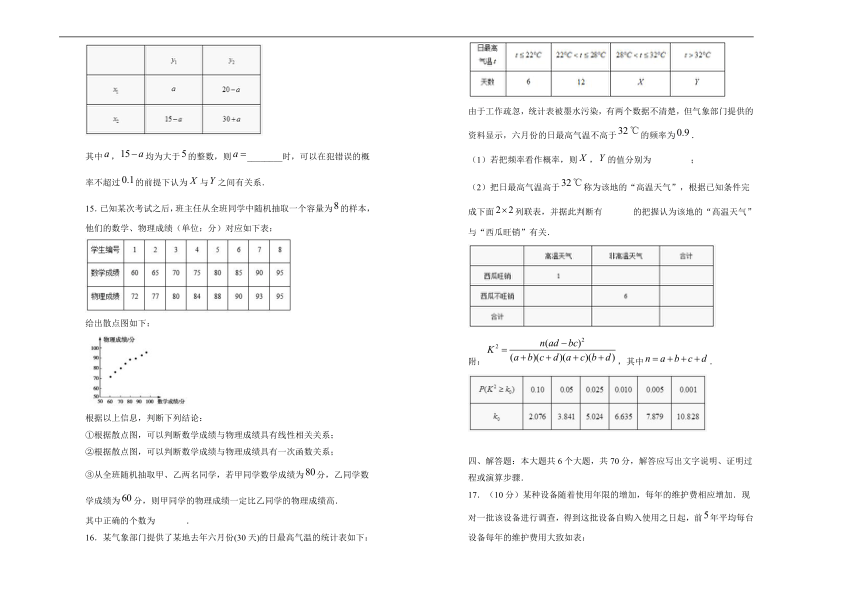
其中,均为大于的整数,则________时,可以在犯错误的概率不超过的前提下认为与之间有关系.
15.已知某次考试之后,班主任从全班同学中随机抽取一个容量为的样本,他们的数学、物理成绩(单位:分)对应如下表:
给出散点图如下:
根据以上信息,判断下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取甲、乙两名同学,若甲同学数学成绩为分,乙同学数学成绩为分,则甲同学的物理成绩一定比乙同学的物理成绩高.
其中正确的个数为 .
16.某气象部门提供了某地去年六月份(30天)的日最高气温的统计表如下:
由于工作疏忽,统计表被墨水污染,有两个数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于的频率为.
(1)若把频率看作概率,则,的值分别为 ;
(2)把日最高气温高于称为该地的“高温天气”,根据已知条件完成下面列联表,并据此判断有 的把握认为该地的“高温天气”与“西瓜旺销”有关.
附:,其中.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前年平均每台设备每年的维护费用大致如表:
给出下列两个条件;线性回归方程为,选择其中的一个作为已知,求下列问题.
(1)求表格中的值;
(2)从这年中随机抽取两年,求平均每台设备每年的维护费用至少有年多于万元的概率;
(3)据此预测第几年开始平均每台设备每年的维护费用超过万元.
参考公式:用最小二乘法求线性回归方程的系数公式:
,.
18.(12分)每个国家对退休年龄都有不一样的规定,从年开始我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取人进行调查,调查情况如表:
(1)从赞成“延迟退休”的人中任选人,此人年龄在的概率为,求出表格中,的值;
(2)在被调查的人中,年龄低于岁的人可以认为“低龄人”,年龄不低于岁的人可以认为“非低龄人”,试作出是否赞成“延迟退休”与“低龄与否”的列联表,并指出有无的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
附:,.
19.(12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表所示:
零件的个数个
加工的时间
(,)
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出关于的线性回归方程;
(3)试预测加工个零件需要多少时间.
20.(12分)年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用模式,其中语文、数学、外语三科为必考科目,满分各分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物门科目中自选门参加考试(选),每科目满分分.为了应对新高考,某高中从高一年级名学生(其中男生人,女生人)中,采用分层抽样的方法从中抽取名学生进行调查.
(1)已知抽取的名学生中含女生人,求的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的列联表.请将列联表补充完整,并判断是否有的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取的选择“地理”的学生中按分层抽样再抽取名,再从这名学生中抽取人了解学生对“地理”的选课意向情况,求人中至少有名男生的概率.
参考公式:.
21.(12分)已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数(个)和温度()的7组观测数据,其散点图如所示:
根据散点图,结合函数知识,可以发现产卵数和温度可用方程来拟合,令,结合样本数据可知与温度可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
27 74 182
表中,.
(1)求和温度的回归方程(回归系数结果精确到);
(2)求产卵数关于温度的回归方程;若该地区一段时间内的气温在之间(包括与),估计该品种一只昆虫的产卵数的范围.(参考数据:,,,,.)
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为.
22.(12分)在年高考数学的全国卷中,文科和理科的题目完全相同,第题考查坐标系和参数方程,第题考查不等式选讲.某校高三质量检测的命题采用了全国卷的模式,在测试结束后,该校数学组教师对该校全体高三学生的得分情况进行了统计,得到两题得分的统计表如下(已知每名学生只做了一道题):
第题的得分统计表
第题得分统计表
(1)完成如下列联表,并判断能否有的把握认为“的选择”与“文、理科的科类”有关;
(2)判断该校全体高三学生第题和第题中哪道题的得分率更高 (得分率题目平均分题目满分,结果精确到);
(3)在按分层抽样的方法在第题得分为的学生中随机抽取名进行单独辅导,并在辅导后随机抽取名学生进行测试,求被抽中进行测试的名学生均为理科生的概率.
附:,其中,.
达标检测卷
成对数据的统计分析(A)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】D
【解析】由散点图可得,从左到右第一个和第三个图中的点大致分布在一条直线附近,两个变量和具有相关性;
而第二个图中的点较分散,两个变量和不具有相关性;
又第一个图中的点由左下方到右上方,两个变量和具有正相关;
第三个图中的点由左上方到右下方,两个变量和具有负相关.
2.【答案】D
【解析】由个数据得到的回归直线不一定过样本中的点,而是这个点到回归直线的距离的平方和最小,所以容易排除选项A、B、C,故选D.
3.【答案】C
【解析】由、两种药物预防某疾病的效果,进行动物试验,分别得到的等高条形图,知:药物的预防效果优于药物的预防效果.
4.【答案】A
【解析】由题意知,,
样本中心点的坐标为,
∵线性回归方程为,∴,解得.
5.【答案】C
【解析】因为
,
所以英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小.
6.【答案】B
【解析】∵,,
∴,∴,
∴点,在回归直线上方,故所求概率为.
7.【答案】D
【解析】分类变量与的随机变量越大,说明“与有关系”的可信度越大,①正确;
,所以,,
所以,的值分别是和,②正确;
回归直线过点,即,解得,即③正确,
所以正确的个数是.
8.【答案】D
【解析】方案一中,没有剔除,线性相关性弱些,成负相关;
方案二中,剔除,线性相关性强些,也成负相关,相关性越强,越接近于,
故选D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】CD
【解析】A中,用相关指数来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于,说明模型的拟合效果越好;
B中,若分类变量和的随机变量的观测值越大,则“与相关”的可信程度越大;
C中,残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适;
D中,两个模型中残差平方和越小的模型拟合的效果越好.
10.【答案】ABC
【解析】根据表中的数据可求得,,由中心点必经过回归直线方程,代入即可求得,A正确;
将点代入可知满足直线方程,B正确;
由回归直线方程可知的系数为正数,说明二者是正相关,C正确;
将代入回归直线方程为中,求得,
所以得到是销售额的估计值为万元,不是一定为万元,D不正确.
11.【答案】ABC
【解析】,,∴直线经过点,
,
,∴,.
∴回归方程为,
当时,,∴直线过点.
12.【答案】ABD
【解析】对于A,根据题意得,用分层抽样在各层的抽样的比为,则在高一年级抽取的人数为人,高二年级抽取的人数为人,高三年级抽取的人数为人,A正确;
对于B,正态分布的正态曲线关于对称,区间和与对称轴距离相等,所以在两个区间上的概率相等,B正确;
对于C,两个随机变量的线性相关性越强,则相关系数的绝对值越接近于,C错误;
对于选项D,若一组数据、、、的众数是,则这组数据的中位数是,所以该选项是正确的.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】由题意可知,,,所以,.
又,所以,
所以当时,.
14.【答案】或
【解析】查表可知,要使在犯错误的概率不超过的前提下认为与之间有关系,
则,
而,
由,得或,
又且,,即,,
故为或时,可以在犯错误的概率不超过的前提下认为与之间有关系.
15.【答案】
【解析】由散点图知,各点都分布在一条直线附近,故可以判断数学成绩与物理成绩具有线性相关关系,但不能判断数学成绩与物理成绩具有一次函数关系,故①正确,②错误;
若甲同学数学成绩为分,乙同学数学成绩为分,则甲同学的物理成绩可能比乙同学的物理成绩高,故③错误,
综上,正确的个数为.
16.【答案】,,
【解析】(1)由已知得,所以,
.
(2)根据题意可得列联表如下,
根据列联表中的数据,得到,
所以有的把握认为该地的“高温天气”与“西瓜旺销”有关.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2);(3)第年.
【解析】选条件,
(1)由,解得.
(2)年中平均每台设备每年的维护费用不超过万元的有年,分别编号为,,,超过万元的有年,编号为,,
随机抽取两年,基本事件为,,,,,,,,,,共个,而且这些基本事件的出现是等可能的,
用表示“抽取的年中平均每台设备每年的维护费用至少有年多于万元”,
则包含的基本事件有,,,,,,,共个,
故.
(3),,,,
,,
∴,,
所以回归方程为,
由题意有,
故第年开始平均每台设备每年的维护费用超过万元.
选条件线性回归方程为,
(1),,
由题意知在回归直线方程上,,解得.
(2)同条件的解答.
(3)由题意知,解得,
所以第年开始平均每台设备每年的维护费用超过万元.
18.【答案】(1),;(2)列联表见解析,有的把握认为.
【解析】(1)因为总共抽取人进行调查,
所以,
因为从赞成“延迟退休”的人中任选人,
此人年龄在的概率为,所以.
(2)是否赞成“延迟退休”与“低龄与否”的列联表如下:
,
所以有的把握认为是否赞成“延迟退休”与“低龄与否”有关.
19.【答案】(1)散点图见解析,(2);(3)小时.
【解析】(1)散点图如图所示.
(2)由表中数据得,,,,
∴,∴,
.
(3)将代入回归直线方程小时,
∴预测加工个零件需要小时.
20.【答案】(1),男生人;(2)列联表见解析,有的把握认为;(3).
【解析】(1)由题意得:,解得,男生人数为人.
(2)列联表为:
,
所以有的把握认为选择科目与性别有关.
(3)从个选择地理的学生中分层抽样抽名,
所以这名学生中有名男生,名女生,
男生编号为,,女生编号为,名学生中再选抽个,
则所有可能的结果为,
至少一名男生的结果为,
所以人中至少一名男生的概率为.
21.【答案】(1);(2),.
【解析】(1)因为与温度可以用线性回归方程来拟合,设.
,
所以,
故关于的线性回归方程为.
(2)由(1)可得,
于是产卵数关于温度的回归方程为,
当时,;
当时,,
因为函数为增函数,
所以气温在之间时,一只该品种昆虫的产卵数的估计范围是内的正整数.
22.【答案】(1)列联表见解析,有的把握认为;(2)第题的得分率更高;(3).
【解析】(1)根据题意填写列联表如下:
由表中数据,计算,
对照临界值得,有的把握认为“的选择”与“文、理科的科类”有关;
(2)第题的平均分为,
得分率为,
第题的平均分为,
得分率为,
所以第题的得分率更高.
(3)由分层抽样的方法可知被选取的名学生中理科生有名,文科生有名,记名理科生为,名文科生为,从这名学生中随机抽取名,
基本事件是:、、、、、、、、、、、、、、共种,
被抽中的名学生中均为理科生的基本事件为、、、、、共种,
故所求概率为.
成对数据的统计分析(A)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.观察下列关于两个变量和的三个散点图,它们从左到右的对应关系依次为( )
A.正相关、负相关、不相关 B.负相关、不相关、正相关
C.负相关、正相关、不相关 D.正相关、不相关、负相关
2.对具有相关关系的两个变量,,收集了组数据:,,,,根据最小二乘法得到线性回归方程,则下列说法一定正确的是( )
A.,都有
B.,使得
C.,都有
D.,使得
3.为考察、两种药物预防某疾病的效果,进行动物试验,分别得到如下等高条形图,根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物、对该疾病均没有预防效果
B.药物、对该疾病均有显著的预防效
C.药物的预防效果优于药物的预防效果
D.药物的预防效果优于药物的预防效果
4.已知一组数据,,,的线性回归方程为,则的值为( )
A. B. C. D.
5.某校学生会为研究该校学生的性别与语文,数学、英语成绩这个变量之间的关系,随机抽查了名学生,得到某次期末考试的成绩数据如表至表,根据表中数据可知该校学生语文、数学、英语这三门学科中( )
表
表
表
A.语文成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
B.数学成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
C.英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
D.英语成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
6.某研究机构在对具有线性相关的两个变量和进行统计分析时,得到如下数据.
由表中数据求得关于的回归方程为,则在这些样本点中任取一点,该点落在回归直线上方的概率为( )
A. B. C. D.
7.下列说法正确的个数是( )
①分类变量与的随机变量越大,说明“与有关系”的可信度越大
②以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,的值分别是和
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为中,,,,则
A. B. C. D.
8.下图是相关变量的散点图,现对这两个变量进行线性相关分析.
方案一:根据图中所有数据,得到线性回归方程,相关系数为;
方案二:剔除点,根据剩下数据得到线性回归直线方程,相关系数为.则( )
A. B.
C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列命题中,正确的命题有( )
A.用相关指数来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于,说明模型的拟合效果越好
B.若分类变量和的随机变量的观测值越大,则“与相关”的可信程度越小
C残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适
D两个模型中残差平方和越小的模型拟合的效果越好
10.己知某产品的销售额与广告费用之间的关系如下表:
若根据表中的数据用最小二乘法求得对的回归直线方程为,则下列说法中正确的是( )
A.的值是
B.该回归直线过点
C.产品的销售额与广告费用成正相关
D.当广告费用为万元时,销售额一定为万元
11.某公司为了增加其商品的销售利润,调查了该商品投入的广告费用与销售利润的统计数据如下表:
由表中数据,得线性回归方程,,则下列结论正确的是( )
A. B.
C直线过点 D.直线过点
12.下列说法正确的是( )
A.某中学高一年级560人,高二年级540人,高三年级520人,用分层抽样的方法抽取容量为81的样本,则在高一、高二、高三三个年级抽取的人数分别为28、27、26
B.正态分布在区间和上取值的概率相等
C.若两个随机变量的线性相关性越强,则相关系数的值越接近于1
D.若一组数据、、、的众数是,则这组数据的中位数是
三、填空题:本大题共4小题,每小题5分.
13.为了研究某班学生的脚长(单位:厘米)和身高(单位:厘米)的关系,从该班随机抽取名学生,根据测量数据的散点图可以看出与之间有线性相关关系,设其回归直线方程为,已知,,.该班某学生的脚长为,据此估计其身高为_______.
14.有两个分类变量与,其一组观测值如下面的列联表所示:
其中,均为大于的整数,则________时,可以在犯错误的概率不超过的前提下认为与之间有关系.
15.已知某次考试之后,班主任从全班同学中随机抽取一个容量为的样本,他们的数学、物理成绩(单位:分)对应如下表:
给出散点图如下:
根据以上信息,判断下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取甲、乙两名同学,若甲同学数学成绩为分,乙同学数学成绩为分,则甲同学的物理成绩一定比乙同学的物理成绩高.
其中正确的个数为 .
16.某气象部门提供了某地去年六月份(30天)的日最高气温的统计表如下:
由于工作疏忽,统计表被墨水污染,有两个数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于的频率为.
(1)若把频率看作概率,则,的值分别为 ;
(2)把日最高气温高于称为该地的“高温天气”,根据已知条件完成下面列联表,并据此判断有 的把握认为该地的“高温天气”与“西瓜旺销”有关.
附:,其中.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前年平均每台设备每年的维护费用大致如表:
给出下列两个条件;线性回归方程为,选择其中的一个作为已知,求下列问题.
(1)求表格中的值;
(2)从这年中随机抽取两年,求平均每台设备每年的维护费用至少有年多于万元的概率;
(3)据此预测第几年开始平均每台设备每年的维护费用超过万元.
参考公式:用最小二乘法求线性回归方程的系数公式:
,.
18.(12分)每个国家对退休年龄都有不一样的规定,从年开始我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取人进行调查,调查情况如表:
(1)从赞成“延迟退休”的人中任选人,此人年龄在的概率为,求出表格中,的值;
(2)在被调查的人中,年龄低于岁的人可以认为“低龄人”,年龄不低于岁的人可以认为“非低龄人”,试作出是否赞成“延迟退休”与“低龄与否”的列联表,并指出有无的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
附:,.
19.(12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表所示:
零件的个数个
加工的时间
(,)
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出关于的线性回归方程;
(3)试预测加工个零件需要多少时间.
20.(12分)年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用模式,其中语文、数学、外语三科为必考科目,满分各分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物门科目中自选门参加考试(选),每科目满分分.为了应对新高考,某高中从高一年级名学生(其中男生人,女生人)中,采用分层抽样的方法从中抽取名学生进行调查.
(1)已知抽取的名学生中含女生人,求的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的列联表.请将列联表补充完整,并判断是否有的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取的选择“地理”的学生中按分层抽样再抽取名,再从这名学生中抽取人了解学生对“地理”的选课意向情况,求人中至少有名男生的概率.
参考公式:.
21.(12分)已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数(个)和温度()的7组观测数据,其散点图如所示:
根据散点图,结合函数知识,可以发现产卵数和温度可用方程来拟合,令,结合样本数据可知与温度可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
27 74 182
表中,.
(1)求和温度的回归方程(回归系数结果精确到);
(2)求产卵数关于温度的回归方程;若该地区一段时间内的气温在之间(包括与),估计该品种一只昆虫的产卵数的范围.(参考数据:,,,,.)
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为.
22.(12分)在年高考数学的全国卷中,文科和理科的题目完全相同,第题考查坐标系和参数方程,第题考查不等式选讲.某校高三质量检测的命题采用了全国卷的模式,在测试结束后,该校数学组教师对该校全体高三学生的得分情况进行了统计,得到两题得分的统计表如下(已知每名学生只做了一道题):
第题的得分统计表
第题得分统计表
(1)完成如下列联表,并判断能否有的把握认为“的选择”与“文、理科的科类”有关;
(2)判断该校全体高三学生第题和第题中哪道题的得分率更高 (得分率题目平均分题目满分,结果精确到);
(3)在按分层抽样的方法在第题得分为的学生中随机抽取名进行单独辅导,并在辅导后随机抽取名学生进行测试,求被抽中进行测试的名学生均为理科生的概率.
附:,其中,.
达标检测卷
成对数据的统计分析(A)答 案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】D
【解析】由散点图可得,从左到右第一个和第三个图中的点大致分布在一条直线附近,两个变量和具有相关性;
而第二个图中的点较分散,两个变量和不具有相关性;
又第一个图中的点由左下方到右上方,两个变量和具有正相关;
第三个图中的点由左上方到右下方,两个变量和具有负相关.
2.【答案】D
【解析】由个数据得到的回归直线不一定过样本中的点,而是这个点到回归直线的距离的平方和最小,所以容易排除选项A、B、C,故选D.
3.【答案】C
【解析】由、两种药物预防某疾病的效果,进行动物试验,分别得到的等高条形图,知:药物的预防效果优于药物的预防效果.
4.【答案】A
【解析】由题意知,,
样本中心点的坐标为,
∵线性回归方程为,∴,解得.
5.【答案】C
【解析】因为
,
所以英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小.
6.【答案】B
【解析】∵,,
∴,∴,
∴点,在回归直线上方,故所求概率为.
7.【答案】D
【解析】分类变量与的随机变量越大,说明“与有关系”的可信度越大,①正确;
,所以,,
所以,的值分别是和,②正确;
回归直线过点,即,解得,即③正确,
所以正确的个数是.
8.【答案】D
【解析】方案一中,没有剔除,线性相关性弱些,成负相关;
方案二中,剔除,线性相关性强些,也成负相关,相关性越强,越接近于,
故选D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
9.【答案】CD
【解析】A中,用相关指数来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于,说明模型的拟合效果越好;
B中,若分类变量和的随机变量的观测值越大,则“与相关”的可信程度越大;
C中,残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适;
D中,两个模型中残差平方和越小的模型拟合的效果越好.
10.【答案】ABC
【解析】根据表中的数据可求得,,由中心点必经过回归直线方程,代入即可求得,A正确;
将点代入可知满足直线方程,B正确;
由回归直线方程可知的系数为正数,说明二者是正相关,C正确;
将代入回归直线方程为中,求得,
所以得到是销售额的估计值为万元,不是一定为万元,D不正确.
11.【答案】ABC
【解析】,,∴直线经过点,
,
,∴,.
∴回归方程为,
当时,,∴直线过点.
12.【答案】ABD
【解析】对于A,根据题意得,用分层抽样在各层的抽样的比为,则在高一年级抽取的人数为人,高二年级抽取的人数为人,高三年级抽取的人数为人,A正确;
对于B,正态分布的正态曲线关于对称,区间和与对称轴距离相等,所以在两个区间上的概率相等,B正确;
对于C,两个随机变量的线性相关性越强,则相关系数的绝对值越接近于,C错误;
对于选项D,若一组数据、、、的众数是,则这组数据的中位数是,所以该选项是正确的.
三、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】由题意可知,,,所以,.
又,所以,
所以当时,.
14.【答案】或
【解析】查表可知,要使在犯错误的概率不超过的前提下认为与之间有关系,
则,
而,
由,得或,
又且,,即,,
故为或时,可以在犯错误的概率不超过的前提下认为与之间有关系.
15.【答案】
【解析】由散点图知,各点都分布在一条直线附近,故可以判断数学成绩与物理成绩具有线性相关关系,但不能判断数学成绩与物理成绩具有一次函数关系,故①正确,②错误;
若甲同学数学成绩为分,乙同学数学成绩为分,则甲同学的物理成绩可能比乙同学的物理成绩高,故③错误,
综上,正确的个数为.
16.【答案】,,
【解析】(1)由已知得,所以,
.
(2)根据题意可得列联表如下,
根据列联表中的数据,得到,
所以有的把握认为该地的“高温天气”与“西瓜旺销”有关.
四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2);(3)第年.
【解析】选条件,
(1)由,解得.
(2)年中平均每台设备每年的维护费用不超过万元的有年,分别编号为,,,超过万元的有年,编号为,,
随机抽取两年,基本事件为,,,,,,,,,,共个,而且这些基本事件的出现是等可能的,
用表示“抽取的年中平均每台设备每年的维护费用至少有年多于万元”,
则包含的基本事件有,,,,,,,共个,
故.
(3),,,,
,,
∴,,
所以回归方程为,
由题意有,
故第年开始平均每台设备每年的维护费用超过万元.
选条件线性回归方程为,
(1),,
由题意知在回归直线方程上,,解得.
(2)同条件的解答.
(3)由题意知,解得,
所以第年开始平均每台设备每年的维护费用超过万元.
18.【答案】(1),;(2)列联表见解析,有的把握认为.
【解析】(1)因为总共抽取人进行调查,
所以,
因为从赞成“延迟退休”的人中任选人,
此人年龄在的概率为,所以.
(2)是否赞成“延迟退休”与“低龄与否”的列联表如下:
,
所以有的把握认为是否赞成“延迟退休”与“低龄与否”有关.
19.【答案】(1)散点图见解析,(2);(3)小时.
【解析】(1)散点图如图所示.
(2)由表中数据得,,,,
∴,∴,
.
(3)将代入回归直线方程小时,
∴预测加工个零件需要小时.
20.【答案】(1),男生人;(2)列联表见解析,有的把握认为;(3).
【解析】(1)由题意得:,解得,男生人数为人.
(2)列联表为:
,
所以有的把握认为选择科目与性别有关.
(3)从个选择地理的学生中分层抽样抽名,
所以这名学生中有名男生,名女生,
男生编号为,,女生编号为,名学生中再选抽个,
则所有可能的结果为,
至少一名男生的结果为,
所以人中至少一名男生的概率为.
21.【答案】(1);(2),.
【解析】(1)因为与温度可以用线性回归方程来拟合,设.
,
所以,
故关于的线性回归方程为.
(2)由(1)可得,
于是产卵数关于温度的回归方程为,
当时,;
当时,,
因为函数为增函数,
所以气温在之间时,一只该品种昆虫的产卵数的估计范围是内的正整数.
22.【答案】(1)列联表见解析,有的把握认为;(2)第题的得分率更高;(3).
【解析】(1)根据题意填写列联表如下:
由表中数据,计算,
对照临界值得,有的把握认为“的选择”与“文、理科的科类”有关;
(2)第题的平均分为,
得分率为,
第题的平均分为,
得分率为,
所以第题的得分率更高.
(3)由分层抽样的方法可知被选取的名学生中理科生有名,文科生有名,记名理科生为,名文科生为,从这名学生中随机抽取名,
基本事件是:、、、、、、、、、、、、、、共种,
被抽中的名学生中均为理科生的基本事件为、、、、、共种,
故所求概率为.
