2021-2022学年沪教新版九年级上册数学第25章 锐角的三角比单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版九年级上册数学第25章 锐角的三角比单元测试卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 551.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 10:51:24 | ||
图片预览




文档简介
2021-2022学年沪教新版九年级上册数学《第25章 锐角的三角比》单元测试卷
一.选择题
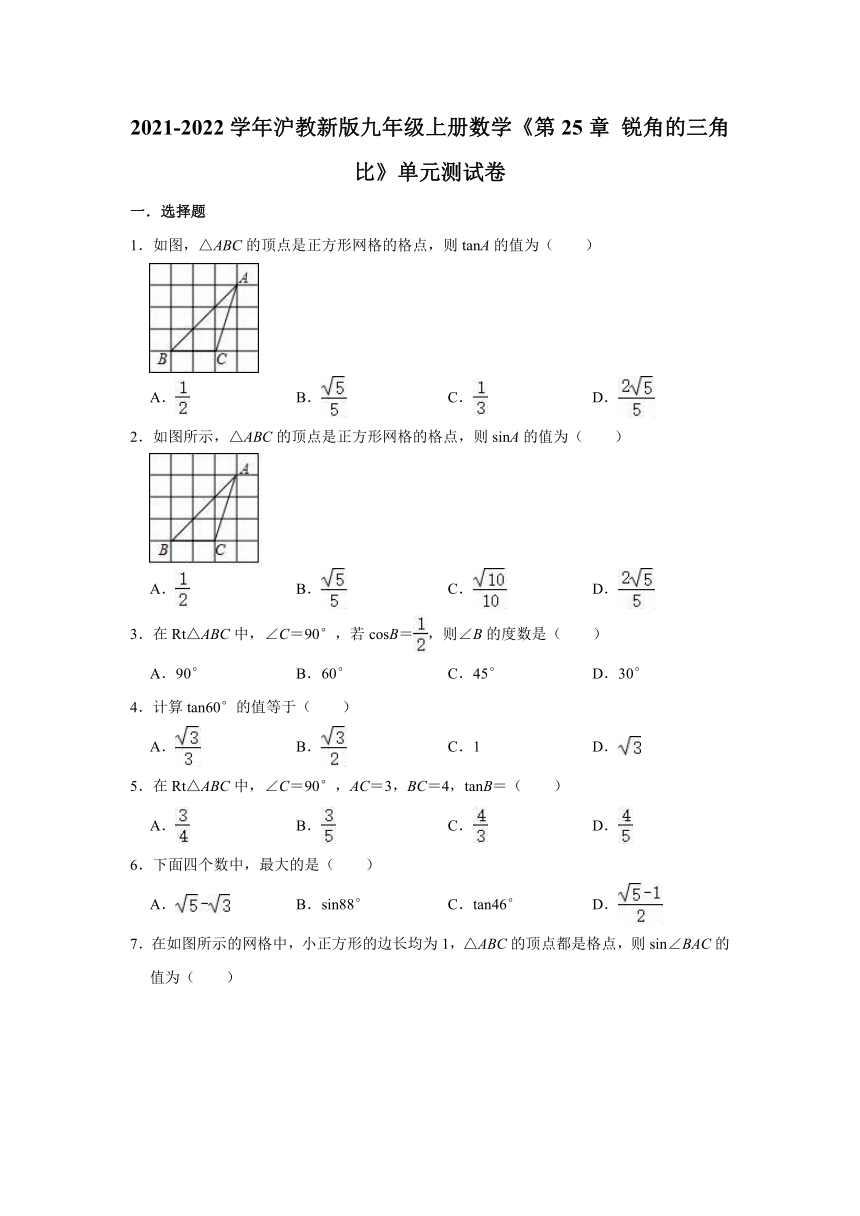
1.如图,△ABC的顶点是正方形网格的格点,则tanA的值为( )
A. B. C. D.
2.如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,若cosB=,则∠B的度数是( )
A.90° B.60° C.45° D.30°
4.计算tan60°的值等于( )
A. B. C.1 D.
5.在Rt△ABC中,∠C=90°,AC=3,BC=4,tanB=( )
A. B. C. D.
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
7.在如图所示的网格中,小正方形的边长均为1,△ABC的顶点都是格点,则sin∠BAC的值为( )
A. B. C.2 D.
8.如图,在△ABC中,∠A=30°,E为AC上一点,且AE:EC=3:1,EF⊥AB于F,连接FC,则tan∠CFB等于( )
A. B. C. D.
9.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A. B.2 C.1 D.
10.如图,△ABC的三个顶点均在格点上,则cosA的值为( )
A. B. C.2 D.
二.填空题
11.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是 .
12.已知:Rt△ABC中,∠C=90°,sinA=,则sinB= .
13.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC= .
14.在Rt△ABC中,∠C=90°,AC=2,BC=3,则cosA= .
15.∠A和∠B是一直角三角形的两锐角,则tan= .
16.若,则锐角α= .
17.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: 0.(可用计算器计算)
18.在网格中,△ABC如图放置,则sinB的值为 .
19.新定义:有一组对角互余的凸四边形称为对余四边形,如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,tanB=,那么边AD的长为 .
20.△ABC中,∠ABC=30°,AB=4,AC=4,则BC= .
三.解答题
21.求下列各式的值:
(1)2sin30°+3cos60°﹣4tan45°;
(2)tan60°﹣(4﹣π)0+2cos30°+()﹣1.
22.计算:()﹣2+×(sin21°13′﹣tan21°)0﹣.
解方程:2(x﹣3)=3x(x﹣3).
23.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
24.计算:.
25.如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:≈1.4,≈1.7,≈2.2)
26.在锐角△ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
27.如图,梯形ABCD中,AD∥BC,AB⊥BC,已知AD=8,BC=12,AB=4.动点E从点B出发,沿射线BA以每秒3个单位的速度移动;同时动点F从点A出发,在线段AD上以每秒2个单位的速度向点D移动.当点F与点D重合时,E、F两点同时停止移动.设点E移动时间为t秒.
(1)求当t为何值时,三点C、E、F共线;
(2)设顺次连接四点B、C、F、E所得封闭图形的面积为S,求出S与t之间的函数关系(要求写出t的取值范围);并求当S取最大值时tan∠BEF的值;
(3)求当t为何值时,以B、E、F为顶点的三角形是等腰三角形?
参考答案与试题解析
一.选择题
1.解:连接CD.
则CD=,AD=2,
则tanA===.
故选:A.
2.解:连接DC,
由网格可得:CD⊥AB,
则DC=,AC=,
故sinA===.
故选:B.
3.解:∵∠C=90°,cosB=,
∴∠B=60°,
故选:B.
4.解:原式=,
故选:D.
5.解:如图所示:
∵在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴tanB==.
故选:A.
6.解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
7.解:作CD⊥AB于D,
由图形可知BC=2,
由勾股定理得,AC==,AB==3,
由三角形的面积公式可得,×2×3=×3×DE,
解得,DE=,
∴sin∠BAC===,
故选:D.
8.解:如图,作出CD⊥AB,垂足为D,则EF∥CD,
∴设EC=x,则AE=3x,sinA=sin30°=EF:AE=1:2,
∴EF=x,
∵cosA=cos30°=AF:AE=,
∴AF=x.
∵EF∥CD,
∴==3,==,
∴FD==x,CD=EF=2x,
∴tan∠CFB==.
故选:C.
9.解:如图,连接BE,与CD交于点F,
∵四边形BCEH是正方形,
∴HF=CF=CH,BF=EF=BE,CH=BE,BE⊥CH,
∴BF=CF,
∵AC∥BH,
∴△ACO∽△BHO,
∴HO:CO=BH:AC=1:3,
∵CF=HF,
∴HO:HF=1:2,
∴HO=OF=,
在Rt△OBF中,tan∠BOF==2
∵∠AOD=∠BOF,
∴tan∠AOD=2.
故选:B.
10.解:过B点作BD⊥AC,如图,
由勾股定理得,
AB==,AC==3,
∴S△ABC=,
∴BD==,
∴AD===2,
cosA===,
故选:D.
二.填空题
11.解:∵∠C=90°,cosA=,AB=15,
∴AC=15×cosA=9,
故答案为9.
12.解:Rt△ABC中,∠C=90°,sinA=,即=,
设CB=5x,则AB=13x,
∴根据勾股定理可得:AC=12x.
∴sinB==.
13.解:∵∠B=90°,sin∠ACB=,
∴=,
∵AB=2,
∴AC=6,
∵AC⊥CD,
∴∠ACD=90°,
∴AD===10,
∴cos∠ADC==.
故答案为:.
14.解:在Rt△ABC中,∠C=90°,AC=2,BC=3,
由勾股定理可得AB=.
则cosA===.
15.解:∵∠A和∠B是一直角三角形的两锐角,
∴∠A+∠B=90°,
∴tan=tan45°=1.
16.解:∵,
∴cosα=,
∴α=45°.
故答案是:45°.
17.解:(Ⅰ)sin60° cos30°﹣= ﹣=﹣=.
(Ⅱ)sin50°cos40°﹣≈0.0868>0.
故答案为:(Ⅰ).
(Ⅱ)>.
18.解:连接A和BC与网格的交点D,设一个小网的边长a,
则AB=a,BD=a,AD=a,
∵AB2=BD2+AD2,
∴可证△ABD为等腰直角三角形,
∴sinB的值为.
故答案为:.
19.解:如图,过端午A作AH⊥BC于H,过点C作CE⊥AD于E,连接AC.
在Rt△ABH中,tanB==,
∴可以假设AH=3k,BH=4k,则AB=5k=10,
∴k=2,
∴AH=6,BH=8,
∵BC=12,
∴CH=BC﹣BH=12﹣8=4,
∴AC===2,
∵∠B+∠D=90°,∠D+∠ECD=90°,
∴∠ECD=∠B,
在Rt△CED中,tan∠ECD==,
∵CD=5,
∴DE=3,CE=4,
∴AE===6,
∴AD=AE+DE=9.
故答案为:9.
20.解:①当∠ACB为锐角时,如图1,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD+DC=6+2=8;
②当∠ACB为钝角时,如图2,过点A作AD⊥BC,交BC的延长线于点D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD﹣DC=6﹣2=4;
因此BC的长为8或4,
故答案为:8或4.
三.解答题
21.解:(1)2sin30°+3cos60°﹣4tan45°
=2×+3×﹣4×1
=1+﹣4
=﹣;
(2)tan60°﹣(4﹣π)0+2cos30°+()﹣1.
=﹣1+2×+4
=﹣1++4
=+3.
22.解:
(1)()﹣2+×(sin21°13′﹣tan21°)0﹣
=4﹣2(+2)×1﹣(1﹣2)
=4﹣2﹣4﹣1+2
=﹣1;
(2)解方程:2(x﹣3)=3x(x﹣3);
(x﹣3)(3x﹣2)=0;
x1=3,x2=;
∴方程的解为:x1=3,x2=.
23.证明:过A作AD⊥BC于D,
在Rt△ABD中,sinB=,
∴AD=ABsinB,
在Rt△ADC中,sinC=,
∴AD=ACsinC,
∴ABsinB=ACsinC,
而AB=c,AC=b,
∴csinB=bsinC,
∴=.
24.解:原式=×1+×+×
=+1+
=3.
25.解:(1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
在Rt△ADC中,AC=4,
∵∠ACB=150°,
∴∠ACD=30°,
∴AD=AC=2,
CD=AC cos30°=4×=2,
在Rt△ABD中,tanB===,
∴BD=16,
∴BC=BD﹣CD=16﹣2;
(2)在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD====2﹣≈0.3.
26.解:(1)过A作AD⊥BC于点D.
∵S△ABC=BC AD=84,
∴×14×AD=84,
∴AD=12.
又∵AB=15,
∴BD==9.
∴CD=14﹣9=5.
在Rt△ADC中,AC==13,
∴tanC==;
(2)过B作BE⊥AC于点E.
∵S△ABC=AC EB=84,
∴BE=,
∴sin∠BAC===.
27.解:(1)依题意得BE=3t,AF=2t,当C,E,F三点共线时,
∵AF∥BC
∴△AEF∽△BEF
∴=即:=;解得t2﹣6t+8=0,t1=2,t2=4
∴当t=2或4秒时,C、E、F三点共线.
(2)当0≤t<时,S=(2t+12)×4﹣(4﹣3t)×2t=3t2+24;
当≤t≤4时,S=(2t+12)×4+12(3t﹣4)×2t=3t2+24
故当t=4时,S最大为72,此时BE=3t=12,tan∠BEF==1.
(3)当E点在线段AB上时,BE=EF,
在Rt△AEF中,AE2+AF2=EF2,
即(4﹣3t)2+(2t)2=(3t)2,解得t1=3﹣,t2=3+(舍去);
当E点在线段AB以外时,
若BE=BF,则BE2=BF2,即(3t)2=42+(2t)2,解得:t=±(舍去负值);
若BE=EF,则BE2=EF2,即(3t)2=(3t﹣4)2+(2t)2,解得t1=3﹣,t2=3+(舍去);
若BF=EF时,AB=AE,即4=3t﹣4,解得t=,
∴t=3﹣,,秒时,以B、E、F为顶点的三角形是等腰三角形.
一.选择题
1.如图,△ABC的顶点是正方形网格的格点,则tanA的值为( )
A. B. C. D.
2.如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,若cosB=,则∠B的度数是( )
A.90° B.60° C.45° D.30°
4.计算tan60°的值等于( )
A. B. C.1 D.
5.在Rt△ABC中,∠C=90°,AC=3,BC=4,tanB=( )
A. B. C. D.
6.下面四个数中,最大的是( )
A. B.sin88° C.tan46° D.
7.在如图所示的网格中,小正方形的边长均为1,△ABC的顶点都是格点,则sin∠BAC的值为( )
A. B. C.2 D.
8.如图,在△ABC中,∠A=30°,E为AC上一点,且AE:EC=3:1,EF⊥AB于F,连接FC,则tan∠CFB等于( )
A. B. C. D.
9.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A. B.2 C.1 D.
10.如图,△ABC的三个顶点均在格点上,则cosA的值为( )
A. B. C.2 D.
二.填空题
11.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是 .
12.已知:Rt△ABC中,∠C=90°,sinA=,则sinB= .
13.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC= .
14.在Rt△ABC中,∠C=90°,AC=2,BC=3,则cosA= .
15.∠A和∠B是一直角三角形的两锐角,则tan= .
16.若,则锐角α= .
17.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: 0.(可用计算器计算)
18.在网格中,△ABC如图放置,则sinB的值为 .
19.新定义:有一组对角互余的凸四边形称为对余四边形,如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,tanB=,那么边AD的长为 .
20.△ABC中,∠ABC=30°,AB=4,AC=4,则BC= .
三.解答题
21.求下列各式的值:
(1)2sin30°+3cos60°﹣4tan45°;
(2)tan60°﹣(4﹣π)0+2cos30°+()﹣1.
22.计算:()﹣2+×(sin21°13′﹣tan21°)0﹣.
解方程:2(x﹣3)=3x(x﹣3).
23.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
24.计算:.
25.如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:≈1.4,≈1.7,≈2.2)
26.在锐角△ABC中,AB=15,BC=14,S△ABC=84,求:
(1)tanC的值;
(2)sinA的值.
27.如图,梯形ABCD中,AD∥BC,AB⊥BC,已知AD=8,BC=12,AB=4.动点E从点B出发,沿射线BA以每秒3个单位的速度移动;同时动点F从点A出发,在线段AD上以每秒2个单位的速度向点D移动.当点F与点D重合时,E、F两点同时停止移动.设点E移动时间为t秒.
(1)求当t为何值时,三点C、E、F共线;
(2)设顺次连接四点B、C、F、E所得封闭图形的面积为S,求出S与t之间的函数关系(要求写出t的取值范围);并求当S取最大值时tan∠BEF的值;
(3)求当t为何值时,以B、E、F为顶点的三角形是等腰三角形?
参考答案与试题解析
一.选择题
1.解:连接CD.
则CD=,AD=2,
则tanA===.
故选:A.
2.解:连接DC,
由网格可得:CD⊥AB,
则DC=,AC=,
故sinA===.
故选:B.
3.解:∵∠C=90°,cosB=,
∴∠B=60°,
故选:B.
4.解:原式=,
故选:D.
5.解:如图所示:
∵在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴tanB==.
故选:A.
6.解:A、﹣≈2.236﹣1.732≈0.504;
B、sin88°≈0.999;
C、tan46°≈1.036;
D、≈≈0.568.
故tan46°最大,
故选:C.
7.解:作CD⊥AB于D,
由图形可知BC=2,
由勾股定理得,AC==,AB==3,
由三角形的面积公式可得,×2×3=×3×DE,
解得,DE=,
∴sin∠BAC===,
故选:D.
8.解:如图,作出CD⊥AB,垂足为D,则EF∥CD,
∴设EC=x,则AE=3x,sinA=sin30°=EF:AE=1:2,
∴EF=x,
∵cosA=cos30°=AF:AE=,
∴AF=x.
∵EF∥CD,
∴==3,==,
∴FD==x,CD=EF=2x,
∴tan∠CFB==.
故选:C.
9.解:如图,连接BE,与CD交于点F,
∵四边形BCEH是正方形,
∴HF=CF=CH,BF=EF=BE,CH=BE,BE⊥CH,
∴BF=CF,
∵AC∥BH,
∴△ACO∽△BHO,
∴HO:CO=BH:AC=1:3,
∵CF=HF,
∴HO:HF=1:2,
∴HO=OF=,
在Rt△OBF中,tan∠BOF==2
∵∠AOD=∠BOF,
∴tan∠AOD=2.
故选:B.
10.解:过B点作BD⊥AC,如图,
由勾股定理得,
AB==,AC==3,
∴S△ABC=,
∴BD==,
∴AD===2,
cosA===,
故选:D.
二.填空题
11.解:∵∠C=90°,cosA=,AB=15,
∴AC=15×cosA=9,
故答案为9.
12.解:Rt△ABC中,∠C=90°,sinA=,即=,
设CB=5x,则AB=13x,
∴根据勾股定理可得:AC=12x.
∴sinB==.
13.解:∵∠B=90°,sin∠ACB=,
∴=,
∵AB=2,
∴AC=6,
∵AC⊥CD,
∴∠ACD=90°,
∴AD===10,
∴cos∠ADC==.
故答案为:.
14.解:在Rt△ABC中,∠C=90°,AC=2,BC=3,
由勾股定理可得AB=.
则cosA===.
15.解:∵∠A和∠B是一直角三角形的两锐角,
∴∠A+∠B=90°,
∴tan=tan45°=1.
16.解:∵,
∴cosα=,
∴α=45°.
故答案是:45°.
17.解:(Ⅰ)sin60° cos30°﹣= ﹣=﹣=.
(Ⅱ)sin50°cos40°﹣≈0.0868>0.
故答案为:(Ⅰ).
(Ⅱ)>.
18.解:连接A和BC与网格的交点D,设一个小网的边长a,
则AB=a,BD=a,AD=a,
∵AB2=BD2+AD2,
∴可证△ABD为等腰直角三角形,
∴sinB的值为.
故答案为:.
19.解:如图,过端午A作AH⊥BC于H,过点C作CE⊥AD于E,连接AC.
在Rt△ABH中,tanB==,
∴可以假设AH=3k,BH=4k,则AB=5k=10,
∴k=2,
∴AH=6,BH=8,
∵BC=12,
∴CH=BC﹣BH=12﹣8=4,
∴AC===2,
∵∠B+∠D=90°,∠D+∠ECD=90°,
∴∠ECD=∠B,
在Rt△CED中,tan∠ECD==,
∵CD=5,
∴DE=3,CE=4,
∴AE===6,
∴AD=AE+DE=9.
故答案为:9.
20.解:①当∠ACB为锐角时,如图1,过点A作AD⊥BC,垂足为D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD+DC=6+2=8;
②当∠ACB为钝角时,如图2,过点A作AD⊥BC,交BC的延长线于点D,
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD﹣DC=6﹣2=4;
因此BC的长为8或4,
故答案为:8或4.
三.解答题
21.解:(1)2sin30°+3cos60°﹣4tan45°
=2×+3×﹣4×1
=1+﹣4
=﹣;
(2)tan60°﹣(4﹣π)0+2cos30°+()﹣1.
=﹣1+2×+4
=﹣1++4
=+3.
22.解:
(1)()﹣2+×(sin21°13′﹣tan21°)0﹣
=4﹣2(+2)×1﹣(1﹣2)
=4﹣2﹣4﹣1+2
=﹣1;
(2)解方程:2(x﹣3)=3x(x﹣3);
(x﹣3)(3x﹣2)=0;
x1=3,x2=;
∴方程的解为:x1=3,x2=.
23.证明:过A作AD⊥BC于D,
在Rt△ABD中,sinB=,
∴AD=ABsinB,
在Rt△ADC中,sinC=,
∴AD=ACsinC,
∴ABsinB=ACsinC,
而AB=c,AC=b,
∴csinB=bsinC,
∴=.
24.解:原式=×1+×+×
=+1+
=3.
25.解:(1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
在Rt△ADC中,AC=4,
∵∠ACB=150°,
∴∠ACD=30°,
∴AD=AC=2,
CD=AC cos30°=4×=2,
在Rt△ABD中,tanB===,
∴BD=16,
∴BC=BD﹣CD=16﹣2;
(2)在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD====2﹣≈0.3.
26.解:(1)过A作AD⊥BC于点D.
∵S△ABC=BC AD=84,
∴×14×AD=84,
∴AD=12.
又∵AB=15,
∴BD==9.
∴CD=14﹣9=5.
在Rt△ADC中,AC==13,
∴tanC==;
(2)过B作BE⊥AC于点E.
∵S△ABC=AC EB=84,
∴BE=,
∴sin∠BAC===.
27.解:(1)依题意得BE=3t,AF=2t,当C,E,F三点共线时,
∵AF∥BC
∴△AEF∽△BEF
∴=即:=;解得t2﹣6t+8=0,t1=2,t2=4
∴当t=2或4秒时,C、E、F三点共线.
(2)当0≤t<时,S=(2t+12)×4﹣(4﹣3t)×2t=3t2+24;
当≤t≤4时,S=(2t+12)×4+12(3t﹣4)×2t=3t2+24
故当t=4时,S最大为72,此时BE=3t=12,tan∠BEF==1.
(3)当E点在线段AB上时,BE=EF,
在Rt△AEF中,AE2+AF2=EF2,
即(4﹣3t)2+(2t)2=(3t)2,解得t1=3﹣,t2=3+(舍去);
当E点在线段AB以外时,
若BE=BF,则BE2=BF2,即(3t)2=42+(2t)2,解得:t=±(舍去负值);
若BE=EF,则BE2=EF2,即(3t)2=(3t﹣4)2+(2t)2,解得t1=3﹣,t2=3+(舍去);
若BF=EF时,AB=AE,即4=3t﹣4,解得t=,
∴t=3﹣,,秒时,以B、E、F为顶点的三角形是等腰三角形.
