浙江省温州市平阳二中高一数学《向量的加法运算及其几何意义》课件
文档属性
| 名称 | 浙江省温州市平阳二中高一数学《向量的加法运算及其几何意义》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 582.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-13 20:57:45 | ||
图片预览




文档简介
(共20张PPT)
2.2.1 向量加法
运算及其几何意义
长度相等 且方向相同 的向量叫做相等向量 。
向量的有关概念
1.向量的定义:
既有大小又有方向的量。
2.相等向量:
数能进行加法运算,与数的运算类比向量能否进行加法运算呢?
问题情境
杭州湾跨海大桥
问题1:建桥之前乘车如何从宁波到达嘉兴?
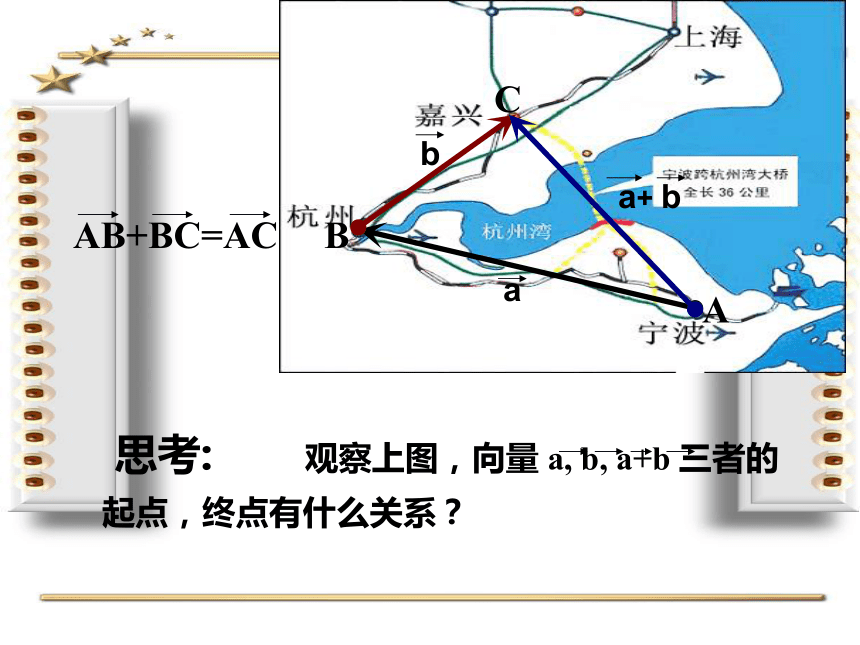
建桥之后可以从宁波直达嘉兴,此时的位移AC与前面两次位移AB, BC的结果有何关系?两次位移的结果可称为两次位移的和,如何用等式来刻画这三个位移的关系
A
B
C
AB+BC=AC
AB+BC=AC
A
B
C
a
b
a+ b
思考: 观察上图,向量 a, b, a+b 三者的起点,终点有什么关系?
A
C
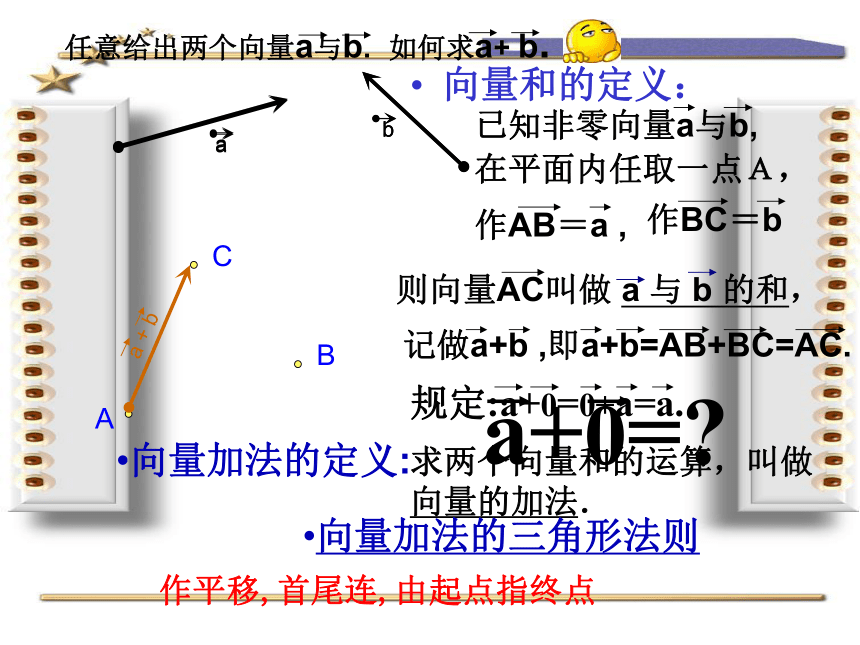
任意给出两个向量a与b.
如何求a+ b.
a
b
a
b
B
a + b
a
b
在平面内任取一点A,
作AB=a ,
作BC=b
则向量AC叫做 a 与 b 的和,
记做a+b ,即a+b=AB+BC=AC.
a+0=
规定:a+0=0+a=a.
求两个向量和的运算,叫做向量的加法.
向量加法的定义:
向量加法的三角形法则
向量和的定义:
已知非零向量a与b,
作平移,首尾连,由起点指终点
A
C
a
b
a
b
B
a + b
a
b
B
O
A
C
a + b
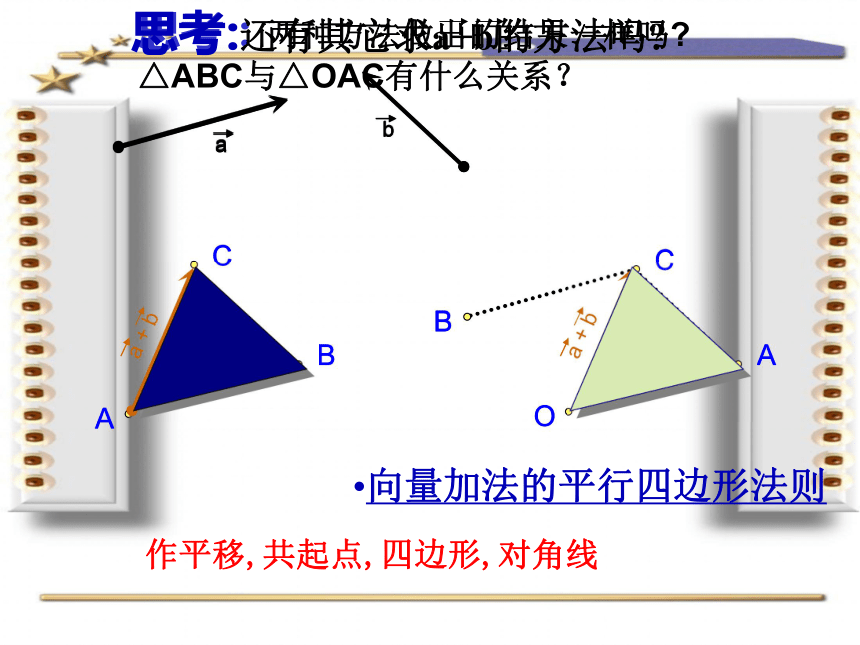
思考:两种方法做出的结果一样吗 △ABC与△OAC有什么关系?
向量加法的平行四边形法则
思考:还有其它求a+b的方法吗
作平移,共起点,四边形,对角线
A
B
C
C
B
b
a
a
b
AC = a + b
AC = a + b
(1)
(2)
A
两向量平行只能用向量加法的三角形法则!
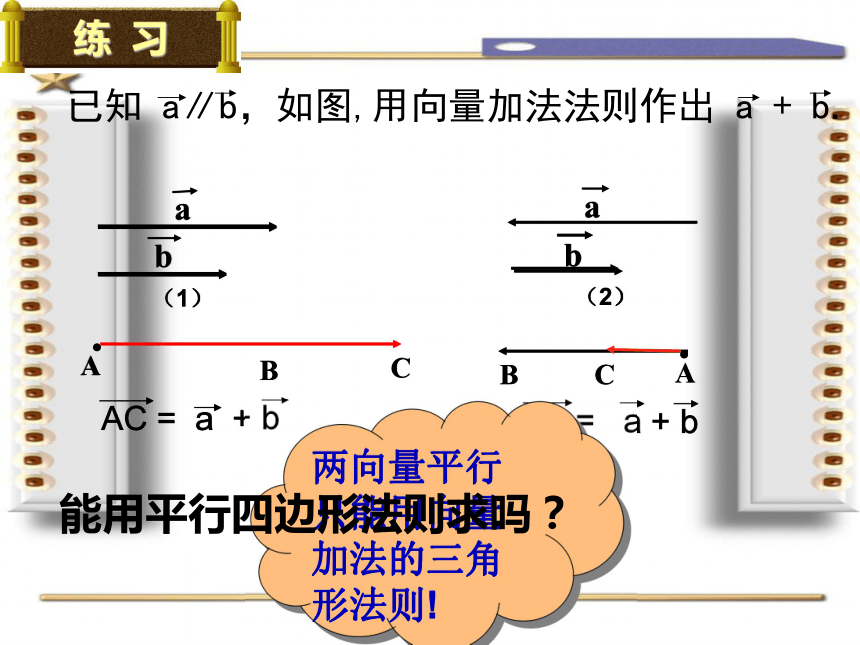
练 习
已知 a∥b,如图,用向量加法法则作出 a + b.
能用平行四边形法则求吗?
当向量 不共线时,和向量的长度 与向量
的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
综合以上探究我们可得结论:
实数的加法
向量的加法
性
质
交换律
结合律
问题2:加法其实我们并不陌生,从小就开始学习数、字母、式的加法,实数的加法有哪些运算性质?向量的加法是否也满足类似的性质?如果满足,具体形式是什么?
?
?
A
O
B
C
M
N
A
B
C
D
a
b
c
实数的加法
向量的加法
性
质
实数的加法有哪些运算性质? 向量的加法是否也满足类似的性 质?如果满足,具体形式是什么?
交换律
结合律
问题:
?
?
如图,O为正六边形A1A2A3A4A5A6的中心,
作出下列向量:
(1)
(2)
(3)
OA2
A1A6
A1A6
A1A2 + A2A3 +……+ An-1An =_______
引申:
A1An
例1:
尝试练习一:
A
B
C
D
E
(1)根据图示填空:
例2. 跨海大桥所在的杭州湾,由于受落潮影响,海水以10km/h的速度向东流,现有一艘小船,在杭州湾海面上巡逻,船以 km/h的速度向正北方向行驶,求船实际航行速度的大小与方向(用与海水速度间的夹角表示).
东
北
分析:首先将实际问题数学化,把三个速度分别用
向量来表示:
设 表示水流速度, 表示船的速度,
三个向量应满足什么关系?
A
B
D
V实
V船
V水
北
东
用AC表示船的实际速度,其方向?
AC=AB+AD
C
练习
如图,在四边形ABCD中,证明
证:
二个定义(向量和的定义、向量加法的定义) 二个运算法则 以及二个运算律
研究方法:
马克思说过:一种科学只有在成功地运用数学时,才算达到完善的地步. 我们今天所学习的向量的加法为研究物理的相关问题提供了一种数学工具,随着对向量研究的逐步深入,向量作为一种新的数学工具被越来越广泛的应用.
小结:
知识内容:
2.2.1 向量加法
运算及其几何意义
长度相等 且方向相同 的向量叫做相等向量 。
向量的有关概念
1.向量的定义:
既有大小又有方向的量。
2.相等向量:
数能进行加法运算,与数的运算类比向量能否进行加法运算呢?
问题情境
杭州湾跨海大桥
问题1:建桥之前乘车如何从宁波到达嘉兴?
建桥之后可以从宁波直达嘉兴,此时的位移AC与前面两次位移AB, BC的结果有何关系?两次位移的结果可称为两次位移的和,如何用等式来刻画这三个位移的关系
A
B
C
AB+BC=AC
AB+BC=AC
A
B
C
a
b
a+ b
思考: 观察上图,向量 a, b, a+b 三者的起点,终点有什么关系?
A
C
任意给出两个向量a与b.
如何求a+ b.
a
b
a
b
B
a + b
a
b
在平面内任取一点A,
作AB=a ,
作BC=b
则向量AC叫做 a 与 b 的和,
记做a+b ,即a+b=AB+BC=AC.
a+0=
规定:a+0=0+a=a.
求两个向量和的运算,叫做向量的加法.
向量加法的定义:
向量加法的三角形法则
向量和的定义:
已知非零向量a与b,
作平移,首尾连,由起点指终点
A
C
a
b
a
b
B
a + b
a
b
B
O
A
C
a + b
思考:两种方法做出的结果一样吗 △ABC与△OAC有什么关系?
向量加法的平行四边形法则
思考:还有其它求a+b的方法吗
作平移,共起点,四边形,对角线
A
B
C
C
B
b
a
a
b
AC = a + b
AC = a + b
(1)
(2)
A
两向量平行只能用向量加法的三角形法则!
练 习
已知 a∥b,如图,用向量加法法则作出 a + b.
能用平行四边形法则求吗?
当向量 不共线时,和向量的长度 与向量
的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
综合以上探究我们可得结论:
实数的加法
向量的加法
性
质
交换律
结合律
问题2:加法其实我们并不陌生,从小就开始学习数、字母、式的加法,实数的加法有哪些运算性质?向量的加法是否也满足类似的性质?如果满足,具体形式是什么?
?
?
A
O
B
C
M
N
A
B
C
D
a
b
c
实数的加法
向量的加法
性
质
实数的加法有哪些运算性质? 向量的加法是否也满足类似的性 质?如果满足,具体形式是什么?
交换律
结合律
问题:
?
?
如图,O为正六边形A1A2A3A4A5A6的中心,
作出下列向量:
(1)
(2)
(3)
OA2
A1A6
A1A6
A1A2 + A2A3 +……+ An-1An =_______
引申:
A1An
例1:
尝试练习一:
A
B
C
D
E
(1)根据图示填空:
例2. 跨海大桥所在的杭州湾,由于受落潮影响,海水以10km/h的速度向东流,现有一艘小船,在杭州湾海面上巡逻,船以 km/h的速度向正北方向行驶,求船实际航行速度的大小与方向(用与海水速度间的夹角表示).
东
北
分析:首先将实际问题数学化,把三个速度分别用
向量来表示:
设 表示水流速度, 表示船的速度,
三个向量应满足什么关系?
A
B
D
V实
V船
V水
北
东
用AC表示船的实际速度,其方向?
AC=AB+AD
C
练习
如图,在四边形ABCD中,证明
证:
二个定义(向量和的定义、向量加法的定义) 二个运算法则 以及二个运算律
研究方法:
马克思说过:一种科学只有在成功地运用数学时,才算达到完善的地步. 我们今天所学习的向量的加法为研究物理的相关问题提供了一种数学工具,随着对向量研究的逐步深入,向量作为一种新的数学工具被越来越广泛的应用.
小结:
知识内容:
同课章节目录
