北师大版九年级上册相似图形培优习题(2)(Word版,附答案)
文档属性
| 名称 | 北师大版九年级上册相似图形培优习题(2)(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 00:00:00 | ||
图片预览


文档简介
北师大版九上数学相似图形培优习题(2)
一、填空题
1.如图,在矩形 中, , ,点 是边 的中点,连接 ,将 沿 折叠得到 , 与 交于点 ,则 的长为 .
2.如图,矩形ABCD中,AD AB , 点E在BC边上,且AE=AD , DF⊥AE于点F , 连接DE , BF , BF的延长线交DE于点O , 交CD于点G . 以下结论:①AF=DC , ②OF:BF=CE:CG , ③S△BCG S△DFG , ④图形中相似三角形有6对,则正确结论的序号是 .
3.如图,在正方形ABCD中,E,F分别是边BC,CD上的一点,EF=BE+DF,在△AEF内部有一点P,且∠APE=∠APF=120°,PA=2 +2,PE=4,则PF2= .
4.如图,在 中, .点D为 边上一点,将 沿 翻折得到 交 于点E.已知 平分 ,则 .
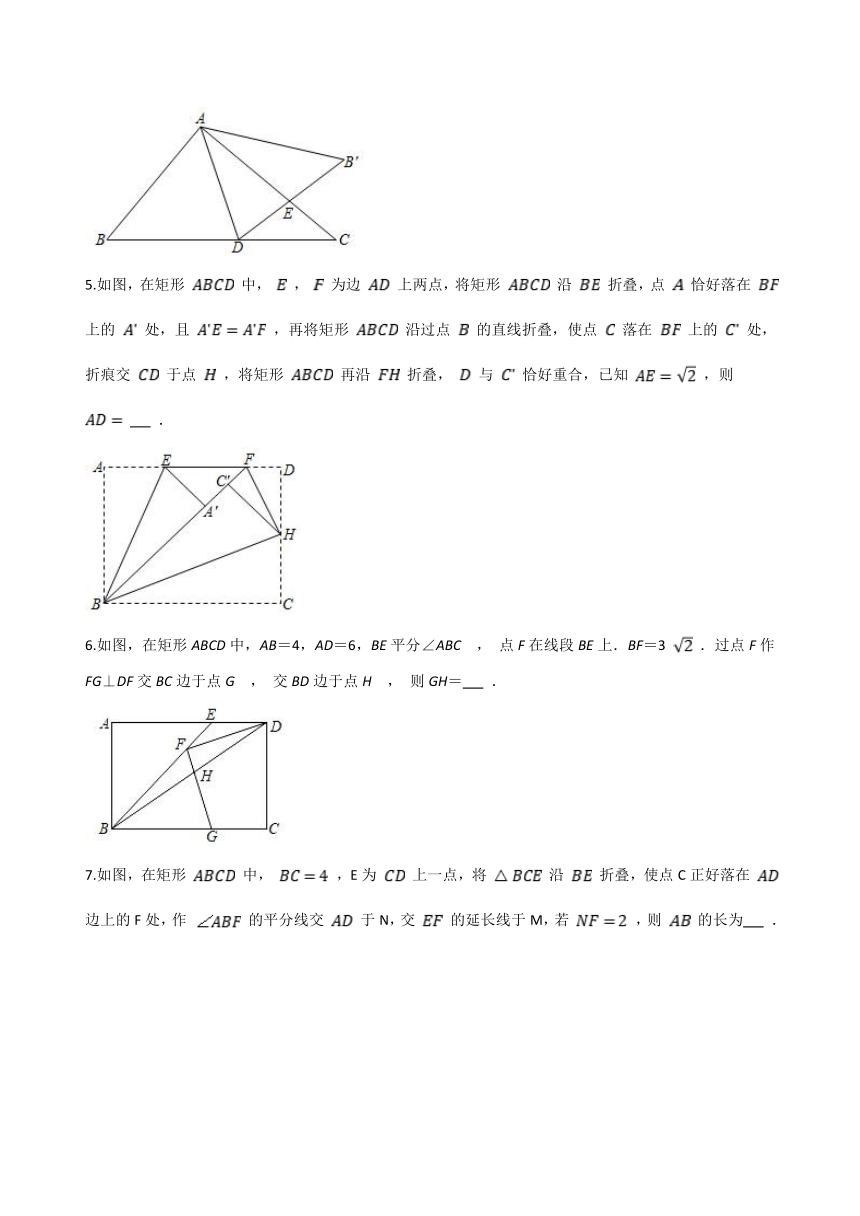
5.如图,在矩形 中, , 为边 上两点,将矩形 沿 折叠,点 恰好落在 上的 处,且 ,再将矩形 沿过点 的直线折叠,使点 落在 上的 处,折痕交 于点 ,将矩形 再沿 折叠, 与 恰好重合,已知 ,则 .
6.如图,在矩形ABCD中,AB=4,AD=6,BE平分∠ABC , 点F在线段BE上.BF=3 .过点F作FG⊥DF交BC边于点G , 交BD边于点H , 则GH= .
7.如图,在矩形 中, ,E为 上一点,将 沿 折叠,使点C正好落在 边上的F处,作 的平分线交 于N,交 的延长线于M,若 ,则 的长为 .
8.已知矩形 , 是 边上一点且 是 边的中点,连接 相交于 两点,则 的面积是 .
9.如图,在矩形 中, , , 是边 上一点,连接 ,将 沿 折叠使点 落在 点,连接 并延长交 于点 ,连接 .若 是以 为腰的等腰三角形,则 的长为 .
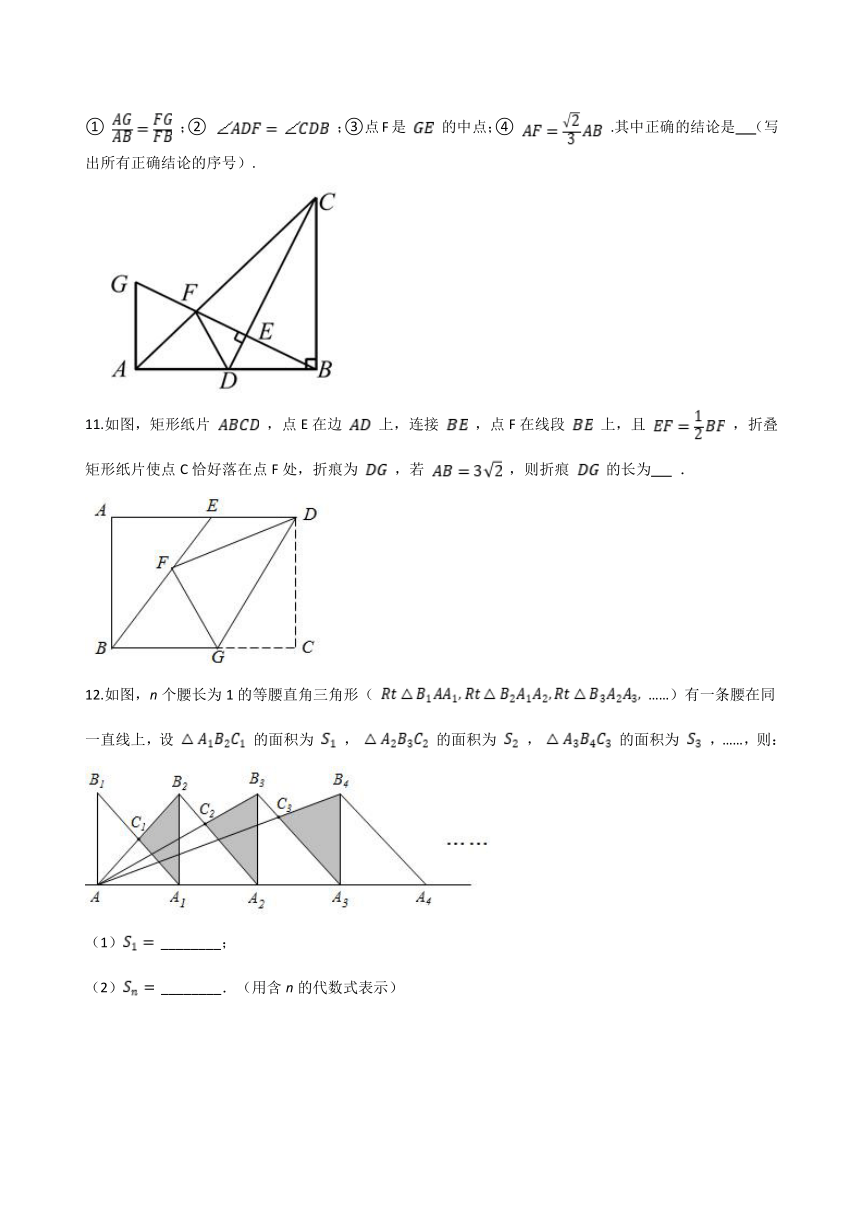
10.如图,在 中, ,点D是 的中点,连结 ,过点B作 ,分别交 于点 ,与过点A且垂直于 的直线相交于点G,连结 ,给出以下几个结论:① ;② ;③点F是 的中点;④ .其中正确的结论是 (写出所有正确结论的序号).
11.如图,矩形纸片 ,点E在边 上,连接 ,点F在线段 上,且 ,折叠矩形纸片使点C恰好落在点F处,折痕为 ,若 ,则折痕 的长为 .
12.如图,n个腰长为1的等腰直角三角形( ……)有一条腰在同一直线上,设 的面积为 , 的面积为 , 的面积为 ,……,则:
(1) ________;
(2) ________.(用含n的代数式表示)
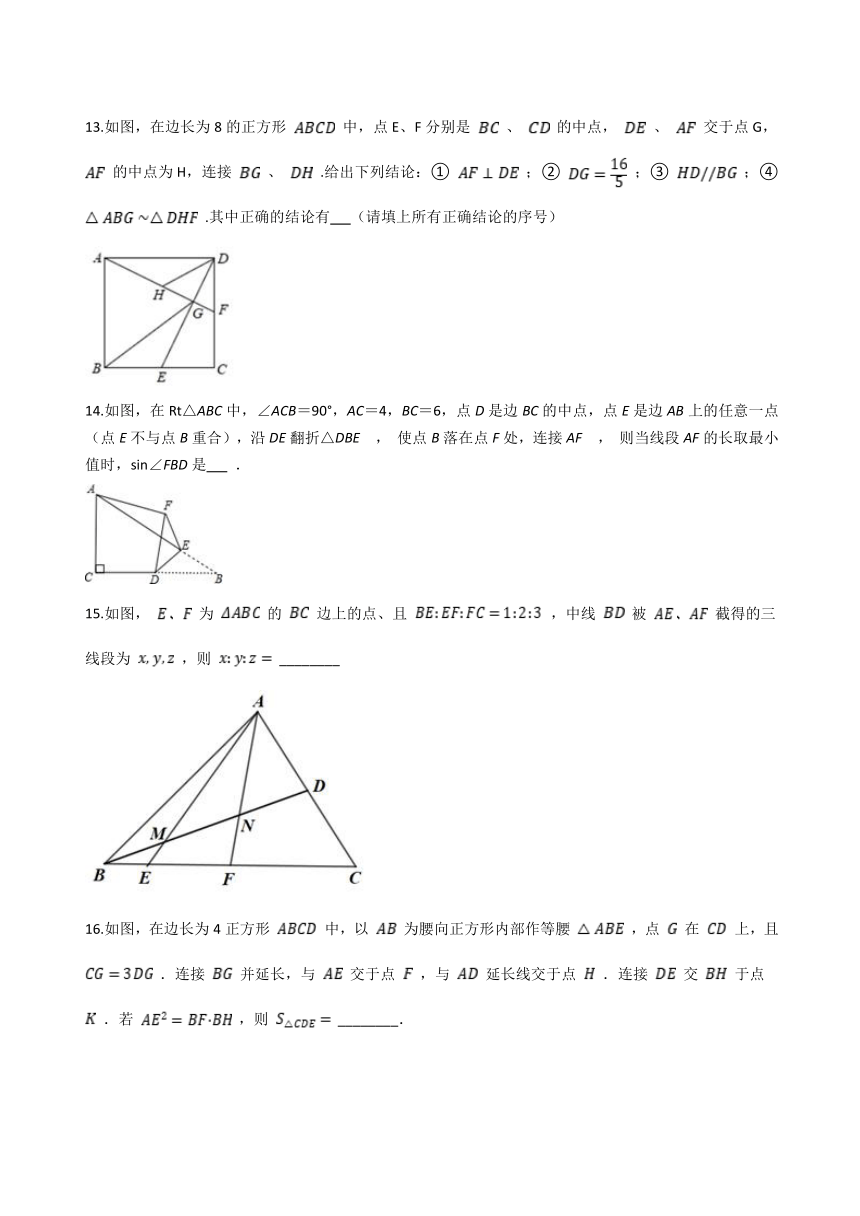
13.如图,在边长为8的正方形 中,点E、F分别是 、 的中点, 、 交于点G, 的中点为H,连接 、 .给出下列结论:① ;② ;③ ;④ .其中正确的结论有 (请填上所有正确结论的序号)
14.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE , 使点B落在点F处,连接AF , 则当线段AF的长取最小值时,sin∠FBD是 .
15.如图, 为 的 边上的点、且 ,中线 被 截得的三线段为 ,则 ________
16.如图,在边长为4正方形 中,以 为腰向正方形内部作等腰 ,点 在 上,且 .连接 并延长,与 交于点 ,与 延长线交于点 .连接 交 于点 .若 ,则 ________.
17.如图,点A在线段BD上,在BD的同侧作等腰 和等腰 ,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:① ;②CD= BE;③MP MD=MA ME;④2CB2=CP CM.其中正确的是________(请填上序号).
二、解答题
18.如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20 ,MD=14 ,求则 NE 的长
19.如图,在 ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。
20.如图
问题背景如图(1),已知 ,求证: ;
尝试应用如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值(提示;连接 );
拓展创新如图(3), 是 内一点, , , , ,直接写出 的长.
21.如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
22.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
23.已知正方形 的对角线 , 相交于点 .
(1)如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;
(2)如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,
①求证: ;
②当 时,求 的长.
24.在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1 .
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.
三、综合题
25.如图
(1).如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F . 求证:AD=BE;
(2).如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,直线AD和直线BE交于点F .
①求证:AD= BE;
②若AB=BC=3 , DE=EC= ,将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
26.已知在 ABC中,O为BC边的中点,连接AO,将 AOC绕点O顺时针方向旋转(旋转角为钝角),得到 EOF,连接AE,CF.
(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是________;
(2)如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.
27.如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是________, ________;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
28.在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,得到△BFE.
(1).点F恰好在AD上;
①如图1,若∠FEB=75°,求出AB:BC的值.
②如图2,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF= BC时,求出AB:BC的值.
(2).E从C到D的运动过程中.
①如图3,若AB=5,BC=8,∠ABF的角平分线交EF的延长线于点M,求M到AD的距离;
②在①的条件下,E从C到D的过程中,直接写出M运动的路径长.
29. 中, , , 、 分别为 、 中点,连接 与 的角平分线 交于点 ,连接 .
(1)如图,求证: .
(2)取 中点 ,连接 、 , 与 交于点 ,如图.
①求证: ;
②求 的值.
30.已知 , 的顶点A在 上,顶点B在 上,且 , .连接 ,与 交于点D.
(1).如图1,若 ,求证: 平分 ;
(2).如图2,若 与 不垂直, 是否仍平分 请作出结论,并说明理由
(3).如图3,若 , ,求 的长.
答案解析部分
一、填空题
1.【答案】
2.【答案】 ①②
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】 3
9.【答案】 或
10.【答案】 ①②④
11.【答案】
12.【答案】 (1)
(2)
13.【答案】 ①④
14.【答案】
15.【答案】
16.【答案】
17.【答案】 ①②③④
二、解答题
18.【答案】 解:连接CM,过点M作MF⊥BD于F
∵△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,AB=20 ,
∴BM= AB=10 ,AC=BC=20,∠CMB=90°,∠BCM= ∠ACB=45°
∵CD⊥BN
∴∠CDB=90°
∴∠CDB+∠CMB=180°
∴C、M、B、D四点共圆
∴∠MDB=∠BCM=45°,∠DCB=∠BMD
∴△DMF为等腰直角三角形
∵MD=14 ,
∴MF=DF=14
在Rt△BMF中,BF=
∴BD=BF+DF=16
∵cos∠CBN=
即
解得:BN=25
∴DN=BN-BD=9
∵∠BNE=∠BNA,而∠DCN+∠BNA=90°
∴∠BNE+∠DCN=90°
∵∠DCN+∠DCB=90°
∴∠BNE=∠DCB
∴∠BNE=∠BMD
∵∠NDE=∠MDB
∴△NDE∽△MDB
∴
即
解得:NE=
故答案为: .
19.【答案】 解:如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.
∵AC⊥BC,
∴∠ACB=90°,
∵BC= ,∠BAC=30°,
∴AB=2BC= ,AC= BC=6,∠ABC=60°,
∵∠EPB=∠EBP=60°,
∴△EPB是等边三角形,
∴∠PEB=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BCE=180°﹣∠ABC=120°,
∴∠EPB+∠BCE=180°,
∴P,B,C,E四点共圆,
∴∠PCB=∠PEB=60°,∠MPC=∠EBC,
∵∠TCB=∠CBT=60°
∴△TCB是等边三角形,
∴∠BCT=60°,∠ACT=30°,BT=BC=AT= ,
∵∠BAG=∠BAC=30°,
∴∠APC=90°,
∴PA=AT cos30°=3,AN=PA cos30°= ,PN= PA= ,PC= PA= ,
∴BN=AB﹣AN= ,
∵∠PBE=∠CBT=60°,
∴∠PBN=∠CBE=∠CPM,
∵∠PCM=∠PNB=90°,
∴△PCM∽△BNP,
∴ ,
∴ ,
∴CM= ,
∵PA⊥PC,CM⊥PC,
∴CM∥PA,
∴ ,
∴AF= AC= .
故答案为 .
20.【答案】 解:问题背景
证明:∵ ,
∴ , ,
∴ , ,
∴ ;
尝试应用
解:如图1,连接 ,
∵ , ,
∴ ,
由(1)知 ,
∴ , ,
在 中, ,
∴ ,
∴ .
∵ , ,
∴ ,
∴ .
拓展创新
如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,
∵∠BAD=30°,
∴∠DAM=60°,
∴∠AMD=30°,
∴∠AMD=∠DBC,
又∵∠ADM=∠BDC=90°,
∴△BDC∽△MDA,
,
又∠BDC=∠ADM,
∴∠BDC+∠CDM=∠ADM+∠CDM,
即∠BDM=∠CDA,
∴△BDM∽△CDA,
=
∵AC=2 ,
∴BM=2 × =6,
∴AM= = =2 ,
.
21.【答案】 (1)解:PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM= BD,PN= AE,
∴PM=PN,
∵PM∥BD,PN∥AE,AE⊥BD,
∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN.
(2)解:∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,
∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PM∥BD;
PN= AE,PN∥AE.
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN
(3)解:PM=kPN
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴ =k.
∴△BCD∽△ACE.
∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PN= AE.
∴PM=kPN.
22.【答案】 (1)解:△BMN是等腰直角三角形.
证明:∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴ .
∴△BMN是等腰直角三角形
(2)解:△MFN∽△BDC.
证明:∵点F,M分别是AB,BC的中点,
∴FM∥AC, .
∵AC=BD,
∴ ,即 .
由(1)知△BMN是等腰直角三角形,
∴ ,即 ,
∴ .
∵AM⊥BC,
∴∠NMF+∠FMB=90°.
∵FM∥AC.
∵∠ACB=∠FMB.
∵∠CEB=90°,
∴∠ACB+∠CBD=90°.
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD.
∴△MFN∽△BDC.
23.【答案】 (1)证明:∵四边形ABCD是正方形.
∴AC⊥BD,OD=OC.
∴∠DOG=∠COE=90°.
∴∠OEC+∠OCE=90°.
∵DF⊥CE.
∴∠OEC+∠ODG=90°.
∴∠ODG=∠OCE.
∴△DOG≌△COE(ASA).
∴OE=OG.
(2)①证明∵OD=OC,∠DOG=∠COE=90°.
又OE=OG.
∴△DOG≌△COE(SAS).
∴∠ODG=∠OCE.
②解:设CH=x,
∵四边形ABCD是正方形,AB=1
∴BH=1-x
∠DBC=∠BDC=∠ACB=45°
∵EH⊥BC
∴∠BEH=∠EBH=45°
∴EH=BH=1-x
∵∠ODG=∠OCE
∴∠BDC-∠ODG=∠ACB-∠OCE
∴∠HDC=∠ECH
∵EH⊥BC
∴∠EHC=∠HCD=90°
∴△CHE∽△DCH
∴ =.
∴HC2=EH·CD
得x2+x-1=0
解得x1=,x2= (舍去).
∴HC=.
24.【答案】 解:(1)①证明:如图1,∵四边形ABCD是正方形,∴OC=OA=OD=OB,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1 , ∴OC1=OC,OD1=OD,∠COC1=∠DOD1 , ∴OC1=OD1 , ∠AOC1=∠BOD1=90°+∠AOD1 , 在△AOC1和△BOD1中, ∴△AOC1≌△BOD1(SAS);②AC1⊥BD1;(2)AC1⊥BD1 . 理由如下:如图2,∵四边形ABCD是菱形,∴OC=OA=AC,OD=OB=BD,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1 , ∴OC1=OC,OD1=OD,∠COC1=∠DOD1 , ∴OC1=OA,OD1=OB,∠AOC1=∠BOD1 , ∴= , ∴△AOC1∽△BOD1 , ∴∠OAC1=∠OBD1 , 又∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD1=90°,∴∠OAB+∠ABP+∠OAC1=90°,∴∠APB=90°∴AC1⊥BD1;∵△AOC1∽△BOD1 , ∴==== , ∴k=;(3)如图3,与(2)一样可证明△AOC1∽△BOD1 , ∴=== , ∴k=;∵△COD绕点O按逆时针方向旋转得到△C1OD1 , ∴OD1=OD,而OD=OB,∴OD1=OB=OD,∴△BDD1为直角三角形,在Rt△BDD1中,BD12+DD12=BD2=100,∴(2AC1)2+DD12=100,∴AC12+(kDD1)2=25.
三、综合题
25.【答案】 (1)证明:∵△ABC与△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACD+∠DCB=∠ECD+∠DCB,
∴∴∠ACD=∠BCE.
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:①∵△ABC与△CDE都是等腰直角三角形,∠ABC=∠DEC=90°,
∴AB=BC,DE=EC,
∴∠ACB=∠DCE=45°, , , ,
∴∠ACD=∠BCE,
∵
∴△ACD∽△BCE,
∴ ,
∴ ;
②当点D落在线段BC上时,
如图所示
则由①得 , .
过点E作EH⊥BC于点H,
∴ (三线合一定理)
∴ (直角三角形斜边的中线等于斜边的一半), .
∴ .
同①原理可得∠ACD=∠BCE=45°, ,
∴△ACD∽△BCE,
∴∠CAD=∠CBE,
又∵∠ADC=∠BDF,
∴∠BFD=∠ACD=45°.
∴∠BFD=∠BCE=45°.
又∵∠DBF=∠EBC,
∴△BDF∽△BEC.
∴ .
∴ .
∴ .
26.【答案】 (1)AE=CF
(2)解:结论成立.
理由:如图2中,
, ,
,
,
,
, ,
,
.
(3)解:如图3中,
由旋转的性质可知 ,
,
,
,
, , ,
,
,
,
,
,
,
.
27.【答案】 (1)ED=BD;
(2)解:①正方形,理由如下:
∵ , 平分 ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴四边形 为矩形,
又∵ ,
∴四边形 为正方形;
②显然,在正方形 中, ,
∴ ,
又∵ ,
∴ ,
由(1)得: 则 为等边三角形,
∴ ,
∵ ,
∴ ,
∴ , ,
又∵ ,
∴ ,
∴ ,
∵ ,
∴
在 与 中,
∴ ,
∴ ,
∴
(3)解:同(2)中①理, ,
∴ , ,
∵ ,
∴ ,
∴ , ,
∴ , ,
∴四边形 为菱形,
∵ 为等边三角形,
∴ ,菱形的边长也为2,
由题意, , ,
∵ ,
∴ ,
即: ,
∴ ,
∵在菱形 中, ,
∴ ,
∴ ,
如图,作 ,
∵ ,
∴ , ,
∵ ,
∴ , ,
在 中, ,
∴ ,
∴ ,
在 中, ,
∴ ,
∵ ,
∴
28.【答案】 (1)解:①如图1中,设 .
∵四边形 是矩形,
∴
由翻折的性质可知,
∴ ,
∴
∴
∵
∴
∴ .
②过点N作NG⊥BF于点G,
∵ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
设AN=x,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG=x,AB=BG=2x,
设FG=y,则AF=2y,
∵AB2+AF2=BF2 ,
∴ ,
解得 .
∴ .
∴
(2)解:①如图3﹣1中,过点M作MK⊥AD于K,MH⊥BA交BA的延长线于H,交CD的延长线于G.
∵四边形ABCD是矩形,
∴∠C=∠BAD=∠ABD=∠ADC=90°,AB=CD=5,AD=BC=8,
∵MH⊥AB,MK⊥AD,
∴∠H=∠HAK=∠AKM=90°,
∴四边形AKMH是矩形,
∴AH=MK,
∵BM平分∠ABF,
∴∠MBH=∠MBF,
∵∠H=∠AFM=90°,BM=BM,
∴△BMH≌△BMF(AAS),
∴BH=BF,
∵BF=BC=8,
∴BH=BC=8,
∴MK=AH=BH﹣AB=8﹣5=3,
∴M到AD的距离为3.
②如图3﹣2中,当点E与D重合时,
∵△BMH≌△BMF,
∴MH=MF,
设MH=MF=m,
∵四边形AHGD是矩形,
∴AH=DG=3,GH=AD=8,∠G=90°,
∵CD=DF=5,GM=GH﹣HM=8﹣m,
在Rt△DGM中,则有 ,
解得m= ,
∴GM=8﹣ = ,
观察图象可知,当E从C到D的过程中,点M运动的路径是线段MG,
∴点M的运动的路径的长为
29.【答案】 (1)∵ , ,
∴ =45°,
∵BF平分 ,
∴ ,
∵ 、 为 、 中点,
∴DE为△ABC的中位线,
∴ ,
∴ ,
∴∠BGD=22.5°,
∴ ,
∴ ,
∴ .
(2)①作 交 于点 ,
∵H为BC中点,∠BAC=90°,AB=AC,
∴∠AHB=90°,AH=BH,
由(1)得∠AGB=90°,
∴ ,
∵ ,
∴ =22.5°,
∵∠AHG+∠AHM=∠GHM=90°,∠BHM+∠AHM=∠AHB=90°,
∴∠AHG=∠BHM,
在△AHG和△BHM中, ,
∴△AHG≌△BHM,
∴ ,GH=MH,
∴△GHM是等腰直角三角形,
∴ ,
∴ .
②如图,过点F作FN⊥BC于N,
∵AB=AC,∠BAC=90°,点H为BC中点,
∴AH=BH,AH⊥BC,
∴△ABH为等腰直角三角形,
∴AB= BH,BC=2BH,
∵DE为△ABC中位线,
∴DE= ,△ADE为等腰直角三角形,
∴AE= ,
∵BF为∠ABC的角平分线,FN⊥BC,∠BAC=90°,
∴FN=AF,∠ABF=∠HBP,
∵AH⊥BC,
∴∠BAF=∠BHP=90°,
∴△ABF∽△HBP,
∴ ,即PH= ,
∵S△ABC= AF·AB+ BC·FN= AB2 ,
∴ BH·AF+2BH·AF=2BH2 ,
∴AF=(2- )BH,
∴EF=AE-AF= ,
.
30.【答案】 (1)证明: , , ,
,
,
.
又 , ,
平分
(2)解: 仍平分 .
理由如下:如图1,作 , .
,
.
又 ,
.
又 ,
.
.
又 , ,
平分 .
(3)解:如图2,作 ,垂足为H.
由(2)知, 平分 ,
.
, ,
.
.
又 ,
.
.
,
设 ,则 ,
, .
.
在 中, .
, ,
, .
在 中, .
一、填空题
1.如图,在矩形 中, , ,点 是边 的中点,连接 ,将 沿 折叠得到 , 与 交于点 ,则 的长为 .
2.如图,矩形ABCD中,AD AB , 点E在BC边上,且AE=AD , DF⊥AE于点F , 连接DE , BF , BF的延长线交DE于点O , 交CD于点G . 以下结论:①AF=DC , ②OF:BF=CE:CG , ③S△BCG S△DFG , ④图形中相似三角形有6对,则正确结论的序号是 .
3.如图,在正方形ABCD中,E,F分别是边BC,CD上的一点,EF=BE+DF,在△AEF内部有一点P,且∠APE=∠APF=120°,PA=2 +2,PE=4,则PF2= .
4.如图,在 中, .点D为 边上一点,将 沿 翻折得到 交 于点E.已知 平分 ,则 .
5.如图,在矩形 中, , 为边 上两点,将矩形 沿 折叠,点 恰好落在 上的 处,且 ,再将矩形 沿过点 的直线折叠,使点 落在 上的 处,折痕交 于点 ,将矩形 再沿 折叠, 与 恰好重合,已知 ,则 .
6.如图,在矩形ABCD中,AB=4,AD=6,BE平分∠ABC , 点F在线段BE上.BF=3 .过点F作FG⊥DF交BC边于点G , 交BD边于点H , 则GH= .
7.如图,在矩形 中, ,E为 上一点,将 沿 折叠,使点C正好落在 边上的F处,作 的平分线交 于N,交 的延长线于M,若 ,则 的长为 .
8.已知矩形 , 是 边上一点且 是 边的中点,连接 相交于 两点,则 的面积是 .
9.如图,在矩形 中, , , 是边 上一点,连接 ,将 沿 折叠使点 落在 点,连接 并延长交 于点 ,连接 .若 是以 为腰的等腰三角形,则 的长为 .
10.如图,在 中, ,点D是 的中点,连结 ,过点B作 ,分别交 于点 ,与过点A且垂直于 的直线相交于点G,连结 ,给出以下几个结论:① ;② ;③点F是 的中点;④ .其中正确的结论是 (写出所有正确结论的序号).
11.如图,矩形纸片 ,点E在边 上,连接 ,点F在线段 上,且 ,折叠矩形纸片使点C恰好落在点F处,折痕为 ,若 ,则折痕 的长为 .
12.如图,n个腰长为1的等腰直角三角形( ……)有一条腰在同一直线上,设 的面积为 , 的面积为 , 的面积为 ,……,则:
(1) ________;
(2) ________.(用含n的代数式表示)
13.如图,在边长为8的正方形 中,点E、F分别是 、 的中点, 、 交于点G, 的中点为H,连接 、 .给出下列结论:① ;② ;③ ;④ .其中正确的结论有 (请填上所有正确结论的序号)
14.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE , 使点B落在点F处,连接AF , 则当线段AF的长取最小值时,sin∠FBD是 .
15.如图, 为 的 边上的点、且 ,中线 被 截得的三线段为 ,则 ________
16.如图,在边长为4正方形 中,以 为腰向正方形内部作等腰 ,点 在 上,且 .连接 并延长,与 交于点 ,与 延长线交于点 .连接 交 于点 .若 ,则 ________.
17.如图,点A在线段BD上,在BD的同侧作等腰 和等腰 ,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:① ;②CD= BE;③MP MD=MA ME;④2CB2=CP CM.其中正确的是________(请填上序号).
二、解答题
18.如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20 ,MD=14 ,求则 NE 的长
19.如图,在 ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。
20.如图
问题背景如图(1),已知 ,求证: ;
尝试应用如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值(提示;连接 );
拓展创新如图(3), 是 内一点, , , , ,直接写出 的长.
21.如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
22.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
23.已知正方形 的对角线 , 相交于点 .
(1)如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;
(2)如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,
①求证: ;
②当 时,求 的长.
24.在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1 .
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.
三、综合题
25.如图
(1).如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F . 求证:AD=BE;
(2).如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,直线AD和直线BE交于点F .
①求证:AD= BE;
②若AB=BC=3 , DE=EC= ,将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
26.已知在 ABC中,O为BC边的中点,连接AO,将 AOC绕点O顺时针方向旋转(旋转角为钝角),得到 EOF,连接AE,CF.
(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是________;
(2)如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.
27.如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)如图1,若 ,则线段 与 的数量关系是________, ________;
(2)如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
①试判断四边形 的形状,并说明理由;
②求证: ;
(3)如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).
28.在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,得到△BFE.
(1).点F恰好在AD上;
①如图1,若∠FEB=75°,求出AB:BC的值.
②如图2,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF= BC时,求出AB:BC的值.
(2).E从C到D的运动过程中.
①如图3,若AB=5,BC=8,∠ABF的角平分线交EF的延长线于点M,求M到AD的距离;
②在①的条件下,E从C到D的过程中,直接写出M运动的路径长.
29. 中, , , 、 分别为 、 中点,连接 与 的角平分线 交于点 ,连接 .
(1)如图,求证: .
(2)取 中点 ,连接 、 , 与 交于点 ,如图.
①求证: ;
②求 的值.
30.已知 , 的顶点A在 上,顶点B在 上,且 , .连接 ,与 交于点D.
(1).如图1,若 ,求证: 平分 ;
(2).如图2,若 与 不垂直, 是否仍平分 请作出结论,并说明理由
(3).如图3,若 , ,求 的长.
答案解析部分
一、填空题
1.【答案】
2.【答案】 ①②
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】 3
9.【答案】 或
10.【答案】 ①②④
11.【答案】
12.【答案】 (1)
(2)
13.【答案】 ①④
14.【答案】
15.【答案】
16.【答案】
17.【答案】 ①②③④
二、解答题
18.【答案】 解:连接CM,过点M作MF⊥BD于F
∵△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,AB=20 ,
∴BM= AB=10 ,AC=BC=20,∠CMB=90°,∠BCM= ∠ACB=45°
∵CD⊥BN
∴∠CDB=90°
∴∠CDB+∠CMB=180°
∴C、M、B、D四点共圆
∴∠MDB=∠BCM=45°,∠DCB=∠BMD
∴△DMF为等腰直角三角形
∵MD=14 ,
∴MF=DF=14
在Rt△BMF中,BF=
∴BD=BF+DF=16
∵cos∠CBN=
即
解得:BN=25
∴DN=BN-BD=9
∵∠BNE=∠BNA,而∠DCN+∠BNA=90°
∴∠BNE+∠DCN=90°
∵∠DCN+∠DCB=90°
∴∠BNE=∠DCB
∴∠BNE=∠BMD
∵∠NDE=∠MDB
∴△NDE∽△MDB
∴
即
解得:NE=
故答案为: .
19.【答案】 解:如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.
∵AC⊥BC,
∴∠ACB=90°,
∵BC= ,∠BAC=30°,
∴AB=2BC= ,AC= BC=6,∠ABC=60°,
∵∠EPB=∠EBP=60°,
∴△EPB是等边三角形,
∴∠PEB=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BCE=180°﹣∠ABC=120°,
∴∠EPB+∠BCE=180°,
∴P,B,C,E四点共圆,
∴∠PCB=∠PEB=60°,∠MPC=∠EBC,
∵∠TCB=∠CBT=60°
∴△TCB是等边三角形,
∴∠BCT=60°,∠ACT=30°,BT=BC=AT= ,
∵∠BAG=∠BAC=30°,
∴∠APC=90°,
∴PA=AT cos30°=3,AN=PA cos30°= ,PN= PA= ,PC= PA= ,
∴BN=AB﹣AN= ,
∵∠PBE=∠CBT=60°,
∴∠PBN=∠CBE=∠CPM,
∵∠PCM=∠PNB=90°,
∴△PCM∽△BNP,
∴ ,
∴ ,
∴CM= ,
∵PA⊥PC,CM⊥PC,
∴CM∥PA,
∴ ,
∴AF= AC= .
故答案为 .
20.【答案】 解:问题背景
证明:∵ ,
∴ , ,
∴ , ,
∴ ;
尝试应用
解:如图1,连接 ,
∵ , ,
∴ ,
由(1)知 ,
∴ , ,
在 中, ,
∴ ,
∴ .
∵ , ,
∴ ,
∴ .
拓展创新
如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,
∵∠BAD=30°,
∴∠DAM=60°,
∴∠AMD=30°,
∴∠AMD=∠DBC,
又∵∠ADM=∠BDC=90°,
∴△BDC∽△MDA,
,
又∠BDC=∠ADM,
∴∠BDC+∠CDM=∠ADM+∠CDM,
即∠BDM=∠CDA,
∴△BDM∽△CDA,
=
∵AC=2 ,
∴BM=2 × =6,
∴AM= = =2 ,
.
21.【答案】 (1)解:PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM= BD,PN= AE,
∴PM=PN,
∵PM∥BD,PN∥AE,AE⊥BD,
∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN.
(2)解:∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,
∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PM∥BD;
PN= AE,PN∥AE.
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN
(3)解:PM=kPN
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴ =k.
∴△BCD∽△ACE.
∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM= BD,PN= AE.
∴PM=kPN.
22.【答案】 (1)解:△BMN是等腰直角三角形.
证明:∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴ .
∴△BMN是等腰直角三角形
(2)解:△MFN∽△BDC.
证明:∵点F,M分别是AB,BC的中点,
∴FM∥AC, .
∵AC=BD,
∴ ,即 .
由(1)知△BMN是等腰直角三角形,
∴ ,即 ,
∴ .
∵AM⊥BC,
∴∠NMF+∠FMB=90°.
∵FM∥AC.
∵∠ACB=∠FMB.
∵∠CEB=90°,
∴∠ACB+∠CBD=90°.
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD.
∴△MFN∽△BDC.
23.【答案】 (1)证明:∵四边形ABCD是正方形.
∴AC⊥BD,OD=OC.
∴∠DOG=∠COE=90°.
∴∠OEC+∠OCE=90°.
∵DF⊥CE.
∴∠OEC+∠ODG=90°.
∴∠ODG=∠OCE.
∴△DOG≌△COE(ASA).
∴OE=OG.
(2)①证明∵OD=OC,∠DOG=∠COE=90°.
又OE=OG.
∴△DOG≌△COE(SAS).
∴∠ODG=∠OCE.
②解:设CH=x,
∵四边形ABCD是正方形,AB=1
∴BH=1-x
∠DBC=∠BDC=∠ACB=45°
∵EH⊥BC
∴∠BEH=∠EBH=45°
∴EH=BH=1-x
∵∠ODG=∠OCE
∴∠BDC-∠ODG=∠ACB-∠OCE
∴∠HDC=∠ECH
∵EH⊥BC
∴∠EHC=∠HCD=90°
∴△CHE∽△DCH
∴ =.
∴HC2=EH·CD
得x2+x-1=0
解得x1=,x2= (舍去).
∴HC=.
24.【答案】 解:(1)①证明:如图1,∵四边形ABCD是正方形,∴OC=OA=OD=OB,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1 , ∴OC1=OC,OD1=OD,∠COC1=∠DOD1 , ∴OC1=OD1 , ∠AOC1=∠BOD1=90°+∠AOD1 , 在△AOC1和△BOD1中, ∴△AOC1≌△BOD1(SAS);②AC1⊥BD1;(2)AC1⊥BD1 . 理由如下:如图2,∵四边形ABCD是菱形,∴OC=OA=AC,OD=OB=BD,AC⊥BD,∴∠AOB=∠COD=90°,∵△COD绕点O按逆时针方向旋转得到△C1OD1 , ∴OC1=OC,OD1=OD,∠COC1=∠DOD1 , ∴OC1=OA,OD1=OB,∠AOC1=∠BOD1 , ∴= , ∴△AOC1∽△BOD1 , ∴∠OAC1=∠OBD1 , 又∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD1=90°,∴∠OAB+∠ABP+∠OAC1=90°,∴∠APB=90°∴AC1⊥BD1;∵△AOC1∽△BOD1 , ∴==== , ∴k=;(3)如图3,与(2)一样可证明△AOC1∽△BOD1 , ∴=== , ∴k=;∵△COD绕点O按逆时针方向旋转得到△C1OD1 , ∴OD1=OD,而OD=OB,∴OD1=OB=OD,∴△BDD1为直角三角形,在Rt△BDD1中,BD12+DD12=BD2=100,∴(2AC1)2+DD12=100,∴AC12+(kDD1)2=25.
三、综合题
25.【答案】 (1)证明:∵△ABC与△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACD+∠DCB=∠ECD+∠DCB,
∴∴∠ACD=∠BCE.
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:①∵△ABC与△CDE都是等腰直角三角形,∠ABC=∠DEC=90°,
∴AB=BC,DE=EC,
∴∠ACB=∠DCE=45°, , , ,
∴∠ACD=∠BCE,
∵
∴△ACD∽△BCE,
∴ ,
∴ ;
②当点D落在线段BC上时,
如图所示
则由①得 , .
过点E作EH⊥BC于点H,
∴ (三线合一定理)
∴ (直角三角形斜边的中线等于斜边的一半), .
∴ .
同①原理可得∠ACD=∠BCE=45°, ,
∴△ACD∽△BCE,
∴∠CAD=∠CBE,
又∵∠ADC=∠BDF,
∴∠BFD=∠ACD=45°.
∴∠BFD=∠BCE=45°.
又∵∠DBF=∠EBC,
∴△BDF∽△BEC.
∴ .
∴ .
∴ .
26.【答案】 (1)AE=CF
(2)解:结论成立.
理由:如图2中,
, ,
,
,
,
, ,
,
.
(3)解:如图3中,
由旋转的性质可知 ,
,
,
,
, , ,
,
,
,
,
,
,
.
27.【答案】 (1)ED=BD;
(2)解:①正方形,理由如下:
∵ , 平分 ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴四边形 为矩形,
又∵ ,
∴四边形 为正方形;
②显然,在正方形 中, ,
∴ ,
又∵ ,
∴ ,
由(1)得: 则 为等边三角形,
∴ ,
∵ ,
∴ ,
∴ , ,
又∵ ,
∴ ,
∴ ,
∵ ,
∴
在 与 中,
∴ ,
∴ ,
∴
(3)解:同(2)中①理, ,
∴ , ,
∵ ,
∴ ,
∴ , ,
∴ , ,
∴四边形 为菱形,
∵ 为等边三角形,
∴ ,菱形的边长也为2,
由题意, , ,
∵ ,
∴ ,
即: ,
∴ ,
∵在菱形 中, ,
∴ ,
∴ ,
如图,作 ,
∵ ,
∴ , ,
∵ ,
∴ , ,
在 中, ,
∴ ,
∴ ,
在 中, ,
∴ ,
∵ ,
∴
28.【答案】 (1)解:①如图1中,设 .
∵四边形 是矩形,
∴
由翻折的性质可知,
∴ ,
∴
∴
∵
∴
∴ .
②过点N作NG⊥BF于点G,
∵ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
设AN=x,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG=x,AB=BG=2x,
设FG=y,则AF=2y,
∵AB2+AF2=BF2 ,
∴ ,
解得 .
∴ .
∴
(2)解:①如图3﹣1中,过点M作MK⊥AD于K,MH⊥BA交BA的延长线于H,交CD的延长线于G.
∵四边形ABCD是矩形,
∴∠C=∠BAD=∠ABD=∠ADC=90°,AB=CD=5,AD=BC=8,
∵MH⊥AB,MK⊥AD,
∴∠H=∠HAK=∠AKM=90°,
∴四边形AKMH是矩形,
∴AH=MK,
∵BM平分∠ABF,
∴∠MBH=∠MBF,
∵∠H=∠AFM=90°,BM=BM,
∴△BMH≌△BMF(AAS),
∴BH=BF,
∵BF=BC=8,
∴BH=BC=8,
∴MK=AH=BH﹣AB=8﹣5=3,
∴M到AD的距离为3.
②如图3﹣2中,当点E与D重合时,
∵△BMH≌△BMF,
∴MH=MF,
设MH=MF=m,
∵四边形AHGD是矩形,
∴AH=DG=3,GH=AD=8,∠G=90°,
∵CD=DF=5,GM=GH﹣HM=8﹣m,
在Rt△DGM中,则有 ,
解得m= ,
∴GM=8﹣ = ,
观察图象可知,当E从C到D的过程中,点M运动的路径是线段MG,
∴点M的运动的路径的长为
29.【答案】 (1)∵ , ,
∴ =45°,
∵BF平分 ,
∴ ,
∵ 、 为 、 中点,
∴DE为△ABC的中位线,
∴ ,
∴ ,
∴∠BGD=22.5°,
∴ ,
∴ ,
∴ .
(2)①作 交 于点 ,
∵H为BC中点,∠BAC=90°,AB=AC,
∴∠AHB=90°,AH=BH,
由(1)得∠AGB=90°,
∴ ,
∵ ,
∴ =22.5°,
∵∠AHG+∠AHM=∠GHM=90°,∠BHM+∠AHM=∠AHB=90°,
∴∠AHG=∠BHM,
在△AHG和△BHM中, ,
∴△AHG≌△BHM,
∴ ,GH=MH,
∴△GHM是等腰直角三角形,
∴ ,
∴ .
②如图,过点F作FN⊥BC于N,
∵AB=AC,∠BAC=90°,点H为BC中点,
∴AH=BH,AH⊥BC,
∴△ABH为等腰直角三角形,
∴AB= BH,BC=2BH,
∵DE为△ABC中位线,
∴DE= ,△ADE为等腰直角三角形,
∴AE= ,
∵BF为∠ABC的角平分线,FN⊥BC,∠BAC=90°,
∴FN=AF,∠ABF=∠HBP,
∵AH⊥BC,
∴∠BAF=∠BHP=90°,
∴△ABF∽△HBP,
∴ ,即PH= ,
∵S△ABC= AF·AB+ BC·FN= AB2 ,
∴ BH·AF+2BH·AF=2BH2 ,
∴AF=(2- )BH,
∴EF=AE-AF= ,
.
30.【答案】 (1)证明: , , ,
,
,
.
又 , ,
平分
(2)解: 仍平分 .
理由如下:如图1,作 , .
,
.
又 ,
.
又 ,
.
.
又 , ,
平分 .
(3)解:如图2,作 ,垂足为H.
由(2)知, 平分 ,
.
, ,
.
.
又 ,
.
.
,
设 ,则 ,
, .
.
在 中, .
, ,
, .
在 中, .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
