5.4 多边形的内角和与外角和(20张ppt)
文档属性
| 名称 | 5.4 多边形的内角和与外角和(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 660.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-06 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第五章 平行四边形
4 多边形的内角和与外角和
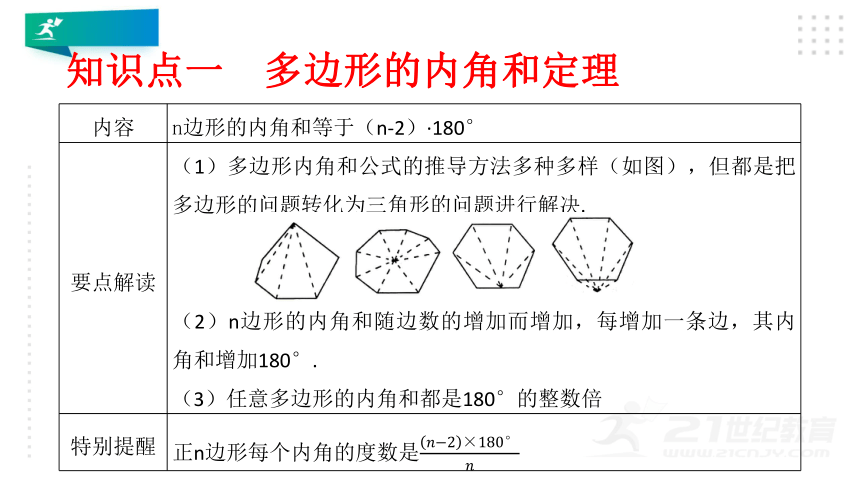
知识点一 多边形的内角和定理
内容 n边形的内角和等于(n-2)·180°
要点解读 (1)多边形内角和公式的推导方法多种多样(如图),但都是把多边形的问题转化为三角形的问题进行解决.
(2)n边形的内角和随边数的增加而增加,每增加一条边,其内角和增加180°.
(3)任意多边形的内角和都是180°的整数倍
特别提醒 正n边形每个内角的度数是
例1 (1)十边形的内角和为__________;
(2)如果一个多边形的内角和为1800°,那么这个多边形的边数是________.
例1 (1)十边形的内角和为__________;
(2)如果一个多边形的内角和为1800°,那么这个多边形的边数是________.
解析 (1)∵n边形的内角和为(n-2)·180°,
∴十边形的内角和为(10-2)×180°=1440°.
(2)设这个多边形的边数为n,则(n-2)·180=1800,解得n=12,
故这个多边形的边数为12.
例1 (1)十边形的内角和为__________;
(2)如果一个多边形的内角和为1800°,那么这个多边形的边数是________.
解析 (1)∵n边形的内角和为(n-2)·180°,
∴十边形的内角和为(10-2)×180°=1440°.
(2)设这个多边形的边数为n,则(n-2)·180=1800,解得n=12,
故这个多边形的边数为12.
方法归纳 (1)运用多边形内角和定理可以求出任意边数的多边形的内角和(2)已知多边形的内角和,根据多边形内角和定理列方程,求出边数.
知识点二 多边形外角的定义、外角和定理
1.多边形内角的一边与另一边的反向延长线所组成的角,叫做这个多边形的外角.
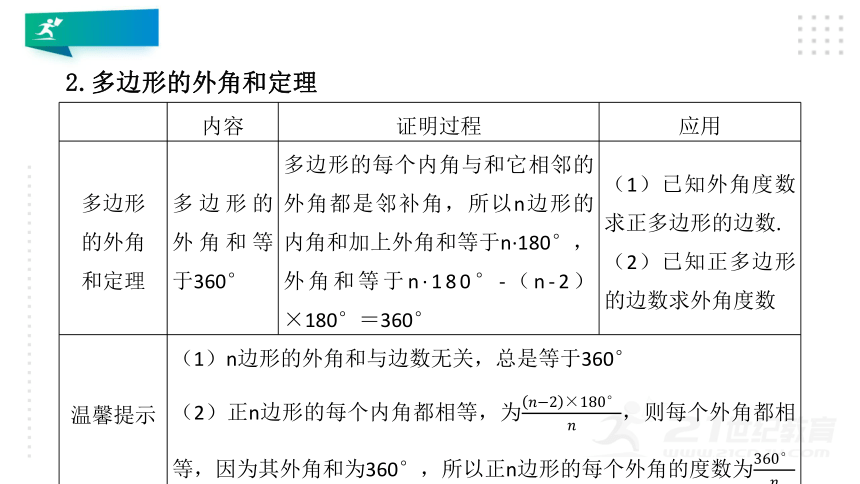
2.多边形的外角和定理
内容 证明过程 应用
多边形 的外角 和定理 多边形的外角和等于360° 多边形的每个内角与和它相邻的外角都是邻补角,所以n边形的内角和加上外角和等于n·180°,外角和等于n·180°-(n-2)×180°=360° (1)已知外角度数求正多边形的边数.
(2)已知正多边形的边数求外角度数
温馨提示 (1)n边形的外角和与边数无关,总是等于360° (2)正n边形的每个内角都相等,为,则每个外角都相等,因为其外角和为360°,所以正n边形的每个外角的度数为 例2(1)一个多边形的每个外角都是45°,求它的边数;
(2)某多边形的内角和与外角和之和为1080°,求该多边形的边数.
例2(1)一个多边形的每个外角都是45°,求它的边数;
(2)某多边形的内角和与外角和之和为1080°,求该多边形的边数.
分析 (1)根据多边形外角和定理列一元一次方程即可求解;
(2)由任意多边形的外角和等于360°,可求出多边形的内角和,再根据多边形内角和定理可求出边数.
解析 (1)设这个多边形的边数为n,由多边形外角和定理得45°·n=360°,解得n=8,所以这个多边形的边数为8.
(2)设这个多边形的边数为n,则(n-2)·180°+360°=1080°,即(n-2)·180°=720°,所以n-2=4,所以n=6.所以这个多边形的边数为6.
解析 (1)设这个多边形的边数为n,由多边形外角和定理得45°·n=360°,解得n=8,所以这个多边形的边数为8.
(2)设这个多边形的边数为n,则(n-2)·180°+360°=1080°,即(n-2)·180°=720°,所以n-2=4,所以n=6.所以这个多边形的边数为6.
方法归纳 当已知一个正多边形的一个外角的度数求多边形的边数时,通常根据多边形的外角和定理来解答,并且与多边形内角和与外角和有关的问题,通常借助方程思想来解答.
经典例题
题型一 应用多边形的内角和公式求边数
例1 若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
题型一 应用多边形的内角和公式求边数
例1 若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
解析 设原多边形的边数为n,则增加一条边后的边数为n+1.由题意得(n+1-2)×180=1440°,解得n=9.
故原多边形的边数为9.
题型一 应用多边形的内角和公式求边数
例1 若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
解析 设原多边形的边数为n,则增加一条边后的边数为n+1.由题意得(n+1-2)×180=1440°,解得n=9.
故原多边形的边数为9.
点拨 本题也可以利用多边形边数每增加1,其内角和就增加180°这一规律来解答,即原多边形的内角和为1440°180°,若设原多边形的边数为n,则可得方程(n-2)×180°=1440°-180°,解得n=9.
题型二 求多边形中角的度数
例2 一个多边形除一个内角∠A外,其余所有内角之和为2190°,求出这个多边形的边数及∠A的度数.
题型二 求多边形中角的度数
例2 一个多边形除一个内角∠A外,其余所有内角之和为2190°,求出这个多边形的边数及∠A的度数.
解析 设此多边形的边数为n,∠A的度数为a,
则(n-2)·180°=2190°+a,即(n-2)·180°=12×180°+30°+a,
∴n-2=13,30°+a=180°,则n=15,a=150°.
故这个多边形的边数是15,∠A的度数是150°.
题型二 求多边形中角的度数
例2 一个多边形除一个内角∠A外,其余所有内角之和为2190°,求出这个多边形的边数及∠A的度数.
解析 设此多边形的边数为n,∠A的度数为a,
则(n-2)·180°=2190°+a,即(n-2)·180°=12×180°+30°+a,
∴n-2=13,30°+a=180°,则n=15,a=150°.
故这个多边形的边数是15,∠A的度数是150°.
点拨 解此类问题时,要注意多边形的内角和为180°的整数倍.
第五章 平行四边形
4 多边形的内角和与外角和
知识点一 多边形的内角和定理
内容 n边形的内角和等于(n-2)·180°
要点解读 (1)多边形内角和公式的推导方法多种多样(如图),但都是把多边形的问题转化为三角形的问题进行解决.
(2)n边形的内角和随边数的增加而增加,每增加一条边,其内角和增加180°.
(3)任意多边形的内角和都是180°的整数倍
特别提醒 正n边形每个内角的度数是
例1 (1)十边形的内角和为__________;
(2)如果一个多边形的内角和为1800°,那么这个多边形的边数是________.
例1 (1)十边形的内角和为__________;
(2)如果一个多边形的内角和为1800°,那么这个多边形的边数是________.
解析 (1)∵n边形的内角和为(n-2)·180°,
∴十边形的内角和为(10-2)×180°=1440°.
(2)设这个多边形的边数为n,则(n-2)·180=1800,解得n=12,
故这个多边形的边数为12.
例1 (1)十边形的内角和为__________;
(2)如果一个多边形的内角和为1800°,那么这个多边形的边数是________.
解析 (1)∵n边形的内角和为(n-2)·180°,
∴十边形的内角和为(10-2)×180°=1440°.
(2)设这个多边形的边数为n,则(n-2)·180=1800,解得n=12,
故这个多边形的边数为12.
方法归纳 (1)运用多边形内角和定理可以求出任意边数的多边形的内角和(2)已知多边形的内角和,根据多边形内角和定理列方程,求出边数.
知识点二 多边形外角的定义、外角和定理
1.多边形内角的一边与另一边的反向延长线所组成的角,叫做这个多边形的外角.
2.多边形的外角和定理
内容 证明过程 应用
多边形 的外角 和定理 多边形的外角和等于360° 多边形的每个内角与和它相邻的外角都是邻补角,所以n边形的内角和加上外角和等于n·180°,外角和等于n·180°-(n-2)×180°=360° (1)已知外角度数求正多边形的边数.
(2)已知正多边形的边数求外角度数
温馨提示 (1)n边形的外角和与边数无关,总是等于360° (2)正n边形的每个内角都相等,为,则每个外角都相等,因为其外角和为360°,所以正n边形的每个外角的度数为 例2(1)一个多边形的每个外角都是45°,求它的边数;
(2)某多边形的内角和与外角和之和为1080°,求该多边形的边数.
例2(1)一个多边形的每个外角都是45°,求它的边数;
(2)某多边形的内角和与外角和之和为1080°,求该多边形的边数.
分析 (1)根据多边形外角和定理列一元一次方程即可求解;
(2)由任意多边形的外角和等于360°,可求出多边形的内角和,再根据多边形内角和定理可求出边数.
解析 (1)设这个多边形的边数为n,由多边形外角和定理得45°·n=360°,解得n=8,所以这个多边形的边数为8.
(2)设这个多边形的边数为n,则(n-2)·180°+360°=1080°,即(n-2)·180°=720°,所以n-2=4,所以n=6.所以这个多边形的边数为6.
解析 (1)设这个多边形的边数为n,由多边形外角和定理得45°·n=360°,解得n=8,所以这个多边形的边数为8.
(2)设这个多边形的边数为n,则(n-2)·180°+360°=1080°,即(n-2)·180°=720°,所以n-2=4,所以n=6.所以这个多边形的边数为6.
方法归纳 当已知一个正多边形的一个外角的度数求多边形的边数时,通常根据多边形的外角和定理来解答,并且与多边形内角和与外角和有关的问题,通常借助方程思想来解答.
经典例题
题型一 应用多边形的内角和公式求边数
例1 若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
题型一 应用多边形的内角和公式求边数
例1 若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
解析 设原多边形的边数为n,则增加一条边后的边数为n+1.由题意得(n+1-2)×180=1440°,解得n=9.
故原多边形的边数为9.
题型一 应用多边形的内角和公式求边数
例1 若一个多边形的边数增加1,其内角和变为1440°,求原多边形的边数.
解析 设原多边形的边数为n,则增加一条边后的边数为n+1.由题意得(n+1-2)×180=1440°,解得n=9.
故原多边形的边数为9.
点拨 本题也可以利用多边形边数每增加1,其内角和就增加180°这一规律来解答,即原多边形的内角和为1440°180°,若设原多边形的边数为n,则可得方程(n-2)×180°=1440°-180°,解得n=9.
题型二 求多边形中角的度数
例2 一个多边形除一个内角∠A外,其余所有内角之和为2190°,求出这个多边形的边数及∠A的度数.
题型二 求多边形中角的度数
例2 一个多边形除一个内角∠A外,其余所有内角之和为2190°,求出这个多边形的边数及∠A的度数.
解析 设此多边形的边数为n,∠A的度数为a,
则(n-2)·180°=2190°+a,即(n-2)·180°=12×180°+30°+a,
∴n-2=13,30°+a=180°,则n=15,a=150°.
故这个多边形的边数是15,∠A的度数是150°.
题型二 求多边形中角的度数
例2 一个多边形除一个内角∠A外,其余所有内角之和为2190°,求出这个多边形的边数及∠A的度数.
解析 设此多边形的边数为n,∠A的度数为a,
则(n-2)·180°=2190°+a,即(n-2)·180°=12×180°+30°+a,
∴n-2=13,30°+a=180°,则n=15,a=150°.
故这个多边形的边数是15,∠A的度数是150°.
点拨 解此类问题时,要注意多边形的内角和为180°的整数倍.
