苏科版七年级数学上册 4.1 从问题到方程(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学上册 4.1 从问题到方程(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
4.1 从问题到方程
七年级(上册)
初中数学
一、情境导入,激发思考
如图,天平左盘内有一袋食盐,天平右盘内有一些砝码,天平平衡时, 你能说出食盐的质量吗?
10g
100g
50g
怎样描述天平平衡时数量之间的相等关系?
天平平衡时
一、情境导入,激发思考
已知天平左盘中放有一袋糖,在天平的右盘内放入砝码,你能称出这袋糖的质量吗?
?
议一议
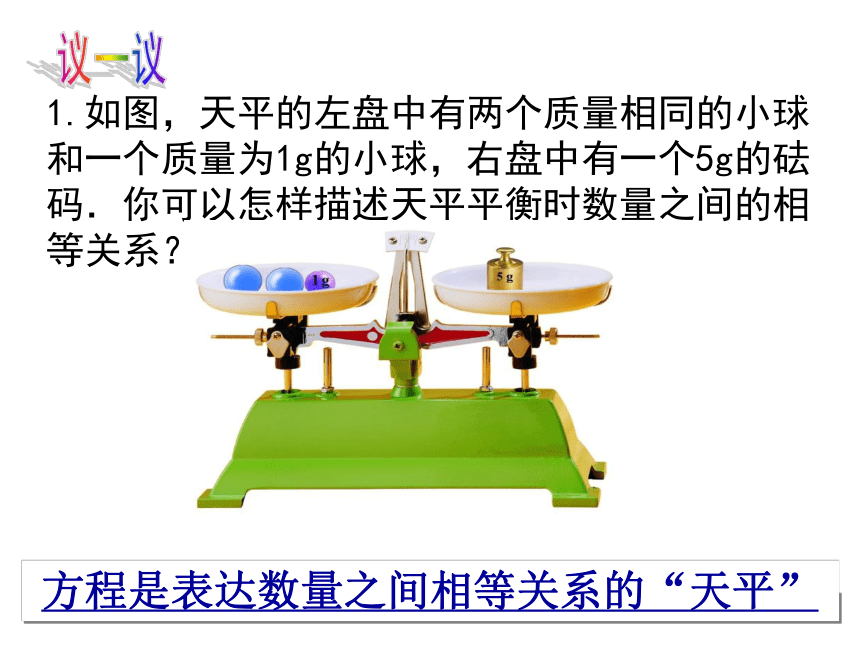
1.如图,天平的左盘中有两个质量相同的小球和一个质量为1g的小球,右盘中有一个5g的砝码.你可以怎样描述天平平衡时数量之间的相等关系?
方程是表达数量之间相等关系的“天平”
2016年里约奥运会上,以小组第四勉强出线的中国女排3比1逆转塞尔维亚女排,强势夺冠。中国女排时隔12年再次成为奥运冠军。女排的不放弃,再一次振奋了国人。
请您欣赏
议一议
2.某排球队在排球联赛中比赛了12场,排球联赛规定:胜一场得2分,负一场得1分,这只排球队一共得了20分.怎样描述其中数量之间的相等关系?
胜场的得分+负场的得分=20
解:设该队胜x场,那么该队负(12-x)场,
可列出方程:____________________
相等关系:
2x+(12-x)=20
想一想
我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?
解:设井深为x尺, 则绳长可表示为 或________尺,
可列方程:________________。
我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺。绳长、井深各几何?
3(x+4)
想一想(根据下列问题中的条件列出方程)
两次测量绳长相等
3(x+4)=4(x+1)
用绳子量井深,把绳折成三段来量,井外余绳四尺;若把绳折成四段来量,井外余绳一尺。绳长、井深各几尺?
4(x+1)
法二:设绳长为y尺,
则井深可表示为 或________尺,
可列方程:________________。
两次测量井深相等
相等关系:____________________
相等关系:____________________
二、合作探究,建构生成
(1)弄清题目中已知什么,求什么,
找出题目中的相等关系;
你觉得“从问题到方程”一般要经历哪些过程
(2)设未知量为x;
(3)用x表示出相关的量,根据相等关系
列出方程。
设
列
相等关系
找
归纳小结
1.我们知道,按下图方式搭n条“小鱼” 需要
[8+6(n-1)]根火柴棒.
搭n条“小鱼”用了140根火柴棒,怎样用方程来描述其中数量之间的相等关系?
试一试
相等关系:____________________,
列出方程:______________________.
8+6(n-1)=140
搭n条小鱼用的火材棒根数=140
试一试
2.今年小红5岁,爸爸32岁.
(1)用代数式分别表示x年后小红与爸爸的年龄.
(2)如果x年后小红的年龄是爸爸年龄的 ,怎样用方程来描述其中数量之间的相等关系?
观察归纳
以上所列方程有什么特点?
叫一元一次方程.
你知道吗
宋元时期,中国数学家创立了“天元术”,用“天元”表示未知数进而建立方程。这种方法的代表作是数学家李冶写的《测圆海镜》,书中所说的“立天元一”相当于“设未知数x。”所以在简称方程时,将未知数称为“元”,如一个未知数的方程叫“一元方程”。而两个以上的未知数,在古代又称为“天元”、“地元”、“人元”。
三、观察归纳,理解概念
练一练
下列各式中,哪些是一元一次方程?
①x=1, ②3x+2=8x-7,③ -2x-3=0 ,
④ x+1>3 , ⑤ 2x+1 , ⑥ ,
⑦
讲一讲
1.你学到了什么数学知识?
2.你体会到了什么数学思想方法
早在300多年前法国数学家笛卡尔有一个伟大的设想:首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为方程问题。虽然笛卡尔的“伟大设想”没有实现,但是充分说明了方程的重要性 。
一个伟大的设想
作业
课本P98 习题1、2、3、4.
谢谢!
4.1 从问题到方程
七年级(上册)
初中数学
一、情境导入,激发思考
如图,天平左盘内有一袋食盐,天平右盘内有一些砝码,天平平衡时, 你能说出食盐的质量吗?
10g
100g
50g
怎样描述天平平衡时数量之间的相等关系?
天平平衡时
一、情境导入,激发思考
已知天平左盘中放有一袋糖,在天平的右盘内放入砝码,你能称出这袋糖的质量吗?
?
议一议
1.如图,天平的左盘中有两个质量相同的小球和一个质量为1g的小球,右盘中有一个5g的砝码.你可以怎样描述天平平衡时数量之间的相等关系?
方程是表达数量之间相等关系的“天平”
2016年里约奥运会上,以小组第四勉强出线的中国女排3比1逆转塞尔维亚女排,强势夺冠。中国女排时隔12年再次成为奥运冠军。女排的不放弃,再一次振奋了国人。
请您欣赏
议一议
2.某排球队在排球联赛中比赛了12场,排球联赛规定:胜一场得2分,负一场得1分,这只排球队一共得了20分.怎样描述其中数量之间的相等关系?
胜场的得分+负场的得分=20
解:设该队胜x场,那么该队负(12-x)场,
可列出方程:____________________
相等关系:
2x+(12-x)=20
想一想
我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?
解:设井深为x尺, 则绳长可表示为 或________尺,
可列方程:________________。
我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺。绳长、井深各几何?
3(x+4)
想一想(根据下列问题中的条件列出方程)
两次测量绳长相等
3(x+4)=4(x+1)
用绳子量井深,把绳折成三段来量,井外余绳四尺;若把绳折成四段来量,井外余绳一尺。绳长、井深各几尺?
4(x+1)
法二:设绳长为y尺,
则井深可表示为 或________尺,
可列方程:________________。
两次测量井深相等
相等关系:____________________
相等关系:____________________
二、合作探究,建构生成
(1)弄清题目中已知什么,求什么,
找出题目中的相等关系;
你觉得“从问题到方程”一般要经历哪些过程
(2)设未知量为x;
(3)用x表示出相关的量,根据相等关系
列出方程。
设
列
相等关系
找
归纳小结
1.我们知道,按下图方式搭n条“小鱼” 需要
[8+6(n-1)]根火柴棒.
搭n条“小鱼”用了140根火柴棒,怎样用方程来描述其中数量之间的相等关系?
试一试
相等关系:____________________,
列出方程:______________________.
8+6(n-1)=140
搭n条小鱼用的火材棒根数=140
试一试
2.今年小红5岁,爸爸32岁.
(1)用代数式分别表示x年后小红与爸爸的年龄.
(2)如果x年后小红的年龄是爸爸年龄的 ,怎样用方程来描述其中数量之间的相等关系?
观察归纳
以上所列方程有什么特点?
叫一元一次方程.
你知道吗
宋元时期,中国数学家创立了“天元术”,用“天元”表示未知数进而建立方程。这种方法的代表作是数学家李冶写的《测圆海镜》,书中所说的“立天元一”相当于“设未知数x。”所以在简称方程时,将未知数称为“元”,如一个未知数的方程叫“一元方程”。而两个以上的未知数,在古代又称为“天元”、“地元”、“人元”。
三、观察归纳,理解概念
练一练
下列各式中,哪些是一元一次方程?
①x=1, ②3x+2=8x-7,③ -2x-3=0 ,
④ x+1>3 , ⑤ 2x+1 , ⑥ ,
⑦
讲一讲
1.你学到了什么数学知识?
2.你体会到了什么数学思想方法
早在300多年前法国数学家笛卡尔有一个伟大的设想:首先把宇宙万物的所有问题都转化为数学问题;其次,把所有的数学问题转化为代数问题;最后,把所有的代数问题转化为方程问题。虽然笛卡尔的“伟大设想”没有实现,但是充分说明了方程的重要性 。
一个伟大的设想
作业
课本P98 习题1、2、3、4.
谢谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
