第3章 圆 名校试题套卷(4) 2021-2022学年北师大版数学九年级下册(word版含答案)
文档属性
| 名称 | 第3章 圆 名校试题套卷(4) 2021-2022学年北师大版数学九年级下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 978.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 08:15:33 | ||
图片预览



文档简介
2021年北师大新版九年级(下)《第3章 圆》名校试题套卷(4)
一、选择题(共10小题)
1.如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )
A.100° B.80° C.50° D.40°
2.如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则的度数为何( )
A.50° B.60° C.100° D.120°
3.已知圆O的半径是4,圆心O到直线L的距离d=6,则直线L与圆O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
4.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5 cm B.8 cm C.10 cm D.12 cm
5.如图⊙O的两条弦AB、CD相交于点E,AC与DB的延长线交于点P,下列结论中成立的是( )
A.CE CD=BE BA B.CE AE=BE DE
C.PC CA=PB BD D.PC PA=PB PD
6.如图,在4×4的方格中,每个小方格都是边长为1的正方形,O、A、B分别是小正方形的顶点,则的长度为( )
A.π B. C.2π D.4π
7.已知a,b,c是△ABC三边的长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5,b=12,c=12
C.a=5,b=12,c=13 D.a=5,b=12,c=14
8.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
9.已知圆O的半径为5,P为圆O内一点,且OP=3,则过点P的所有弦中,弦长是整数的共有( )
A.4条 B.3条 C.2条 D.1条
10.如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A',再以点B为圆心,BA'为半径作圆弧交CB的延长线于B',依次进行.得到螺旋线,再顺次连接EA',AB',BC',CD',DE',得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
A. B. C. D.
二、填空题(共10小题)
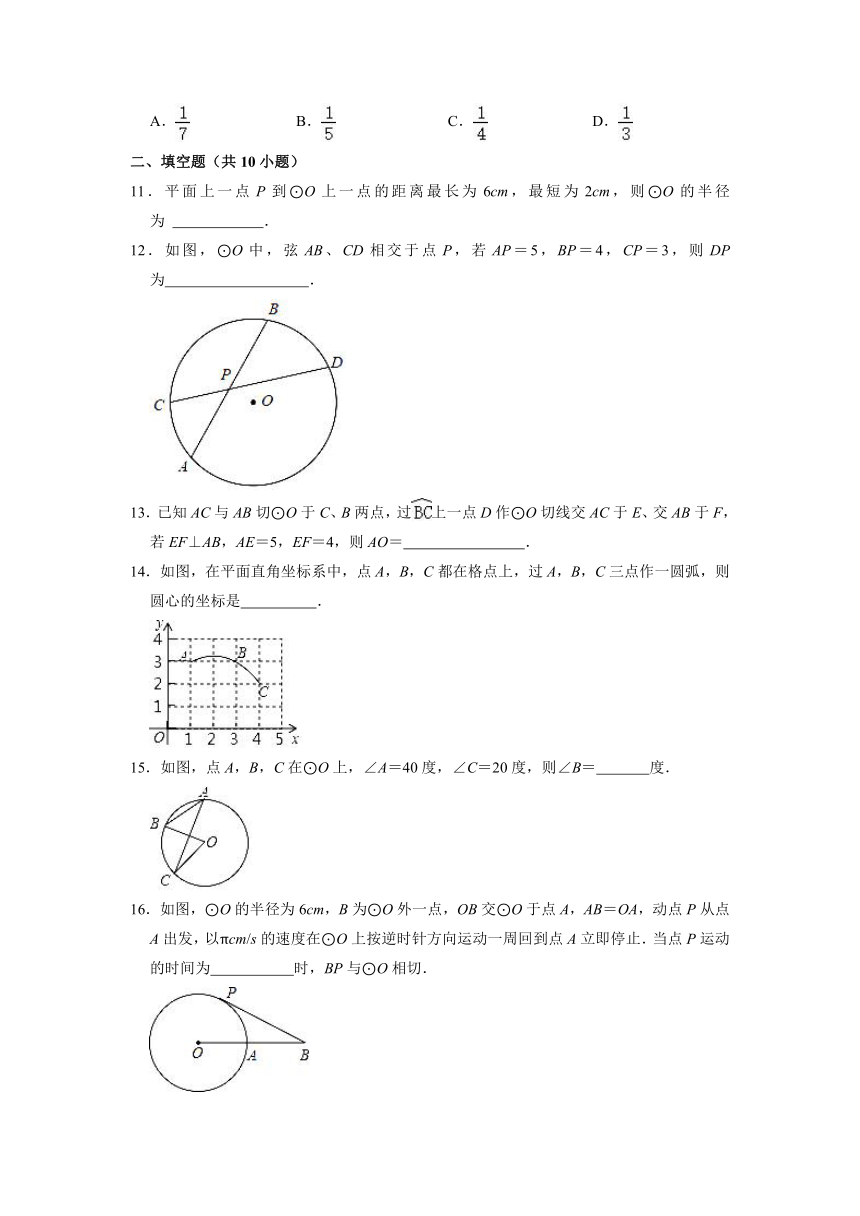
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为 .
12.如图,⊙O中,弦AB、CD相交于点P,若AP=5,BP=4,CP=3,则DP为 .
13.已知AC与AB切⊙O于C、B两点,过上一点D作⊙O切线交AC于E、交AB于F,若EF⊥AB,AE=5,EF=4,则AO= .
14.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
15.如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B= 度.
16.如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 时,BP与⊙O相切.
17.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是 .
18.在△ABC中,AB=4,BC=5,AC=6,⊙O是△ABC的内切圆,则⊙O的半径为 .
19.如图,⊙O1与⊙O2交于点A,B,延长⊙O2的直径CA交⊙O1于点D,延长⊙O2的弦CB交⊙O1于点E.已知AC=6,AD:BC:BE=1:1:5,则DE的长是 .
20.如图,已知⊙O的半径为2,正方形ABCD的边长为2,过点O作OM⊥AB,垂足为M,AM=BM,若阴影部分的面积为2,则OM长为 .
三、解答题(共10小题)
21.如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
(1)求证:DE所在的直线为⊙O的切线.
(2)若AB=10,BE=5,求OF的长.
22.如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
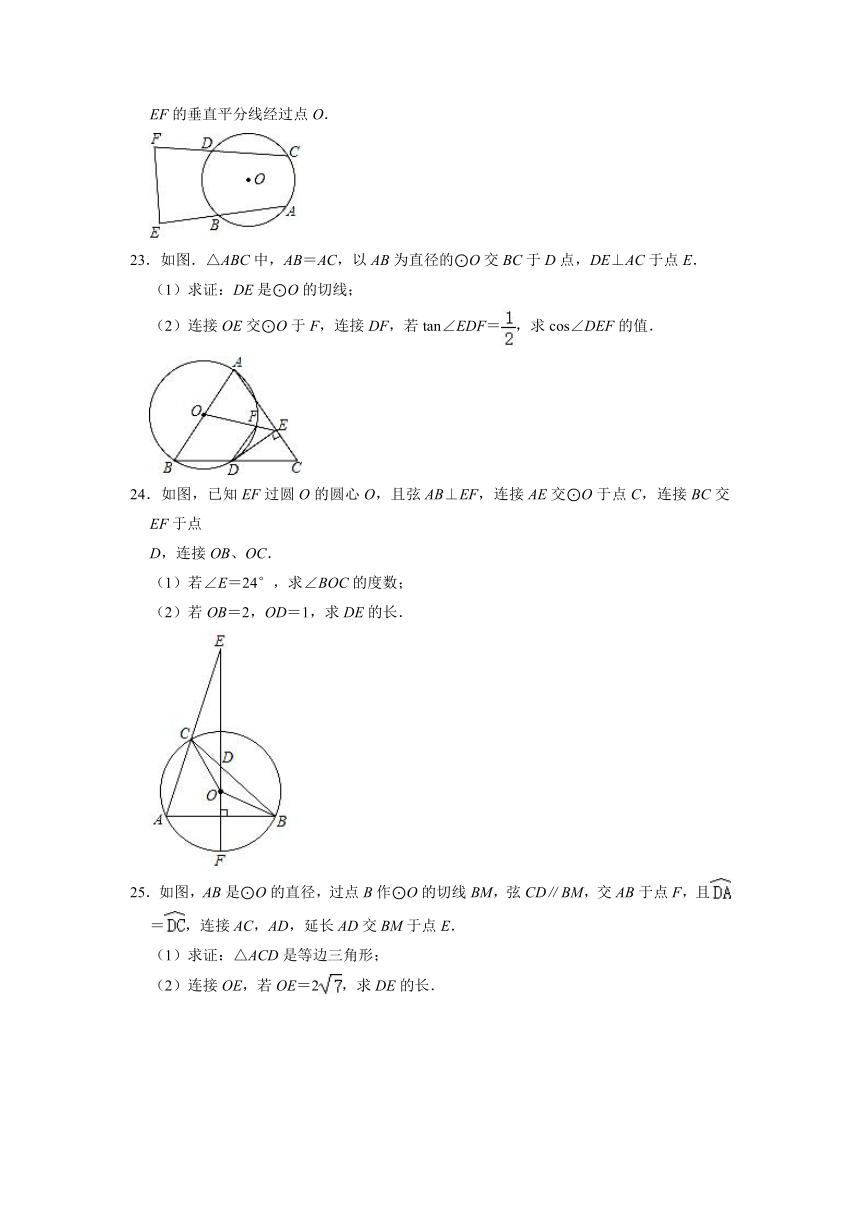
23.如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)连接OE交⊙O于F,连接DF,若tan∠EDF=,求cos∠DEF的值.
24.如图,已知EF过圆O的圆心O,且弦AB⊥EF,连接AE交⊙O于点C,连接BC交EF于点
D,连接OB、OC.
(1)若∠E=24°,求∠BOC的度数;
(2)若OB=2,OD=1,求DE的长.
25.如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)连接OE,若OE=2,求DE的长.
26.如图,已知,BE是⊙O的直径,BC切⊙O于B,弦DE∥OC,连接CD并延长交BE的延长线于点A.
(1)证明:CD是⊙O的切线;
(2)若AD=2,AE=1,求CD的长.
27.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
28.每个小方格都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图.
(1)将菱形OABC先向右平移4个单位,再向上平移2个单位,得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2,并求出点B旋转到B2的路径长.
29.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A等于66°,求∠ADB的度数.
30.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
2021年北师大新版九年级(下)《第3章 圆》名校试题套卷(4)
参考答案与试题解析
一、选择题(共10小题)
1.如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )
A.100° B.80° C.50° D.40°
【解答】解:∵OA=OB,
∴∠BAO=∠ABO=50°,
∴∠AOB=180°﹣50°﹣50°=80°,
∴∠ACB=∠AOB=40°.
故选:D.
2.如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则的度数为何( )
A.50° B.60° C.100° D.120°
【解答】解:∵∠A=70°,∠B=60°,
∴∠C=50°.
∵此圆与直线BC相切于C点,
∴的度数=2∠C=100°.
故选:C.
3.已知圆O的半径是4,圆心O到直线L的距离d=6,则直线L与圆O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
【解答】解:根据圆心到直线的距离6大于圆的半径4,则直线和圆相离.
故选:A.
4.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5 cm B.8 cm C.10 cm D.12 cm
【解答】解:设光盘的圆心为O,如图所示:
过点O作OA垂直直尺于点A,连接OB,设OB=x,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴AB=×(10﹣2)=4,
∵刻度尺宽2cm,
∴OA=x﹣2,
在Rt△OAB中,
OA2+AB2=OB2,即(x﹣2)2+42=x2,
解得:x=5.
∴该光盘的直径是10cm.
故选:C.
5.如图⊙O的两条弦AB、CD相交于点E,AC与DB的延长线交于点P,下列结论中成立的是( )
A.CE CD=BE BA B.CE AE=BE DE
C.PC CA=PB BD D.PC PA=PB PD
【解答】解:由相交弦定理知,CE ED=BE AE,由切割线定理知,PC PA=PB PD,只有D正确.
故选:D.
6.如图,在4×4的方格中,每个小方格都是边长为1的正方形,O、A、B分别是小正方形的顶点,则的长度为( )
A.π B. C.2π D.4π
【解答】解:
∵AC=OC=OD=BD=2,
∠C=∠D=90°,
∴∠AOC=∠BOD=45°,
∴∠AOB=90°,
由勾股定理得:AO=BO=2,
的长度为=,
故选:B.
7.已知a,b,c是△ABC三边的长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5,b=12,c=12
C.a=5,b=12,c=13 D.a=5,b=12,c=14
【解答】解:∵外接圆的圆心在△ABC一条边上,
∴△ABC是直角三角形.
∴当a=5,b=12,c=13时,a2+b2=c2,
则△ABC是直角三角形.
故选:C.
8.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
【解答】解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
∵AB,AE都为圆的切线
∴AE=AB
∵OB=OE,AO=AO
∴△ABO≌△AEO(SSS)
∴∠OAB=∠OAE
∴AO⊥BE
在直角△AOB里AO2=OB2+AB2
∵OB=1,AB=3
∴AO=
易证明△BOF∽△AOB
∴BO:AO=OF:OB
∴1:=OF:1
∴OF=
sin∠CBE==
故选:D.
9.已知圆O的半径为5,P为圆O内一点,且OP=3,则过点P的所有弦中,弦长是整数的共有( )
A.4条 B.3条 C.2条 D.1条
【解答】解:如图,过P作弦AB⊥OP,交⊙O于A、B,连接OA,
Rt△OAP中,OP=3,OA=5,
根据勾股定理,得AP==4,
即由垂径定理得:AB=2AP=8,
∵最长的弦是直径,长度是10,
∴过点P的弦的长度都在8~10之间,
∴弦长为8、9、10,
当弦长为8、10时,过P点的弦分别为弦AB和过P点的直径,分别有一条;
当弦长为9时,根据圆的对称性知,符合条件的弦应该有两条;
故弦长为整数的弦共有4条,
故选:A.
10.如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A',再以点B为圆心,BA'为半径作圆弧交CB的延长线于B',依次进行.得到螺旋线,再顺次连接EA',AB',BC',CD',DE',得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
A. B. C. D.
【解答】解:设五边形的边长为a.则S1=﹣ a2 sin72°,
S2=﹣ a 2a sin72°,
S3=﹣ a 3a sin72°,
S4=﹣ a 4a sin72°,
S5=﹣ a 5a sin72°,
∵S5﹣S2=1,
∴5πa2﹣πa2﹣a2 sin72°=1,
∴ π a2﹣a2 sin72°=1,
∴S4﹣S3=πa2﹣πa2﹣a2sin72°=π a2﹣a2sin72°=,
故选:D.
二、填空题(共10小题)
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为 4cm或2cm .
【解答】解:当点P在圆内时,则直径=6+2=8cm,因而半径是4cm;当点P在圆外时,直径=6﹣2=4cm,因而半径是2cm.
所以⊙O的半径为4或2cm.
12.如图,⊙O中,弦AB、CD相交于点P,若AP=5,BP=4,CP=3,则DP为 .
【解答】解:由相交弦定理得,PA PB=PC PD,
∴5×4=3×DP,
解得,DP=,
故答案为:.
13.已知AC与AB切⊙O于C、B两点,过上一点D作⊙O切线交AC于E、交AB于F,若EF⊥AB,AE=5,EF=4,则AO= .
【解答】解:如图,
∵EF⊥AB,AE=5,EF=4,
∴AF2=52﹣42=9,
∴AF=3;
∵ABACEF分别是⊙O的切线,
∴AB=AC,EG=EC,FG=FB;
OC⊥EC,OG⊥GE,OB⊥FB;
∴AE+EF+AF=AC+AB=2AC=12,
∴AC=6;
在RT△EOC与RT△EOG中,
,
∴RT△EOC≌RT△EOG(HL),
同理可证:△GOF≌△BOF,
∴=4R(R为⊙O的半径),
∵,
,
∴4R+6=6R,
∴R=3,
由勾股定理得:
AO2=62+32,
∴AO=,
股改答案为.
14.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 (2,1) .
【解答】解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
15.如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B= 60 度.
【解答】解:如图,连接OA,
∵OA=OC,
∴∠OAC=∠C=20°,
∴∠OAB=60°,
∵OA=OB,
∴∠B=∠OAB=60°,
故答案为:60.
16.如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 2秒或10秒 时,BP与⊙O相切.
【解答】解:连接OP
∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=6cm,
弧AP==2π,
∵圆的周长为:12π,
∴点P运动的距离为2π或12π﹣2π=10π;
∴当t=2秒或10秒时,有BP与⊙O相切.
故答案为:2秒或10秒.
17.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是 π .
【解答】解:将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A'重合,则转过的距离是圆的周长是π,因而点A'对应的实数是π.
故答案为:π.
18.在△ABC中,AB=4,BC=5,AC=6,⊙O是△ABC的内切圆,则⊙O的半径为 .
【解答】解:设切点分别为点D,E,F,连接AO,BO,CO,OD,OF,OE,过点A作AH⊥BC于点H,
设BH=x,则CH=BC﹣x=5﹣x,
∵AH2=AB2﹣BH2,AH2=AC2﹣CE2,
∴AB2﹣BH2=AC2﹣CE2,
即16﹣x2=36﹣(5﹣x)2,
解得:x=,
∴AH=,
∴S△ABC=BC AH=,
∵⊙O是△ABC的内切圆,
∴OD⊥AB,OF⊥AC,OE⊥BC,OF=OD=OE,
∵S△ABC=S△AOB+S△BOC+S△AOC,
∴=×(AB+BC+AC)×OD,
解得:OD=,
∴⊙O的半径为,
故答案为:.
19.如图,⊙O1与⊙O2交于点A,B,延长⊙O2的直径CA交⊙O1于点D,延长⊙O2的弦CB交⊙O1于点E.已知AC=6,AD:BC:BE=1:1:5,则DE的长是 9 .
【解答】解:连接AB,在圆内接四边形ABED中,∠BAC=∠E,∠ABC=∠EDC,
因为AC为⊙O2直径,则∠ABC=90°,于是△ABC∽△EDC,
因为AD:BC:BE=1:1:5,
所以,设AD=x,BC=x,BE=5x;
于是:=,即6x2=36+6x,x2﹣x﹣6=0,
解得x=3,x=﹣2(负值舍去),
在Rt△EDC中,ED==9.
20.如图,已知⊙O的半径为2,正方形ABCD的边长为2,过点O作OM⊥AB,垂足为M,AM=BM,若阴影部分的面积为2,则OM长为 ﹣1+ .
【解答】解:设AD交⊙O于E,BC交⊙O于F,连接EF,OE,OF,延长OM交EF于H.
由题意EF∥AB,EF=AB=2,
∵OM⊥AB,
∴OH⊥EF,
∴EH=FH=1,
∴sin∠FOH==,
∴∠FOH=30°,
∵OE=OF,OH⊥EF,
∴∠EOH=∠FOH=30°,
∴∠EOF=60°,
∴OH=FH=,
∵阴影部分的面积为2,设AE=BF=MH=x,
∴2(2﹣x)﹣(﹣×22)=2,
解得x=1﹣+,
∴OM=OH﹣MH=﹣(1﹣+)=﹣1+,
故答案为﹣1+.
三、解答题(共10小题)
21.如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
(1)求证:DE所在的直线为⊙O的切线.
(2)若AB=10,BE=5,求OF的长.
【解答】(1)证明:连接OD;如图1所示:
∵O、D分别是AB、AC的中点,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOE=∠BEO;
∵OB=OE,
∴∠AOD=∠DOE,
在△OAD和△OED中,,
∴△OAD≌△OED(SAS),
∴∠OED=∠OAD=90°,DE=AD,
∴DE为⊙O的切线.
(2)解:连接AE,如图2所示:
∵AB=10,BE=5,
∴AE=5,
∴AE=AB,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠ABC=30°,
∴BC=,
∵OD∥BC,OD=BC=,
∴OD:BE=OF:EF=2:3;
∵OE=AB=5,
∴OF=2.
22.如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
【解答】解:过点O作OG⊥CF于点G,OH⊥AE于点H,连接OF、OE,
∴由垂径定理可知:BH=AB,DG=CD,
∵AB=CD,
∴BH=DG,
∵OD=OB,
∴由勾股定理可知:OG2=OH2,
∵BE=DF,
∴BE+BH=DF+DG,
∴EH=FG,
∴在Rt△OEH与Rt△OFG中,
由勾股定理可知:OE2=OF2,
∴OE=OF,
∴△OFE是等腰三角形,
∴由等腰三角形的三线合一可知:EF的垂直平分线过O点.
23.如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)连接OE交⊙O于F,连接DF,若tan∠EDF=,求cos∠DEF的值.
【解答】解:(1)连接OD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∴OD为△ABC的中位线
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)作OM⊥DF于M,ON⊥OF于N.
∵OD=OF,OM⊥DF,
∴DM=MF,设DM=MF=a,
∵∠EDF=∠DOE,
∴tan∠DOM=tan∠EDF=,
∴OM=2a,AD=OF=a,
∵ DF OM= OF DN,
∴DN=a,
∵∠ODN+∠DON=90°,∠DON+∠OED=90°,
∴∠ODN=∠OED,
∴cos∠DEF=sin∠DON==.
24.如图,已知EF过圆O的圆心O,且弦AB⊥EF,连接AE交⊙O于点C,连接BC交EF于点
D,连接OB、OC.
(1)若∠E=24°,求∠BOC的度数;
(2)若OB=2,OD=1,求DE的长.
【解答】解:(1)∵EF⊥AB,
∴∠A+∠E=90°,
∵∠E=24°,
∴∠A=90°﹣∠E=66°,
∴∠BOC=2∠A=132°;
(2)∵OB=OC,
∴∠OCB=∠OBC,
在△OBC中,∠COB=,
∵∠E=90°﹣∠A,∠A=∠BOC,
∴∠OCB=∠E,
∵∠COD=∠EOC,
∴△COD∽△EOC,
∴,
∵OB=2,OD=1,
∴,
解得OE=4,
∴DE=OE﹣OD=3.
25.如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)连接OE,若OE=2,求DE的长.
【解答】(1)证明:∵=,
∴DA=DC
∵BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BM,
∴CD⊥AB,
∴=,
∴AD=AC,
∴AD=AC=CD,即△ACD是等边三角形;
(2)连接OE,作OG⊥AD于G,
由(1)得,∠EAB=30°,
∴AB=BE,
∴OB=BE,
由勾股定理得,(BE)2+BE2=(2)2,
解得,BE=4,
则AB=4,AE=8,
在Rt△AOG中,∠OAG=30°,OA=2,
∴AG=3,
∴AD=6,
∴DE=AE﹣AD=2.
26.如图,已知,BE是⊙O的直径,BC切⊙O于B,弦DE∥OC,连接CD并延长交BE的延长线于点A.
(1)证明:CD是⊙O的切线;
(2)若AD=2,AE=1,求CD的长.
【解答】(1)证明:连接OD,
∵ED∥OC,
∴∠COB=∠DEO,∠COD=∠EDO,
∵OD=OE,
∴∠DEO=∠EDO,
∴∠COB=∠COD,
在△BCO和△DCO中,
∴△BCO≌△DCO(SAS),
∴∠CDO=∠CBO,
∵BC为圆O的切线,
∴BC⊥OB,即∠CBO=90°,
∴∠CDO=90°,
又∵OD为圆的半径,
∴CD为圆O的切线;
(2)解:∵CD,BC分别切⊙O于D,B,
∴CD=BC,
∵AD2=AE AB,即22=1 AB,
∴AB=4,
设CD=BC=x,则AC=2+x,
∵A2C=AB2+BC2
∴(2+x)2=42+x2,
解得:x=3,
∴CD=3.
27.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
【解答】解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4(m),
在Rt△AEO中,OE===3(m),
∴ED=OD﹣OE=5﹣3=2(m),
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
28.每个小方格都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图.
(1)将菱形OABC先向右平移4个单位,再向上平移2个单位,得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2,并求出点B旋转到B2的路径长.
【解答】解:(1)
根据平移的性质可知B1的坐标:(8,6)
(2)点B旋转到B2的路径就是一段弧长.
根据勾股定理得OB=
根据弧长公式得:.
29.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A等于66°,求∠ADB的度数.
【解答】(1)证明:∵DB平分∠ADC,
∴=,
∵OC⊥BD,
∴=,
∴=,
∴AB=CD;
(2)解:∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°﹣∠A=114°,
∵=,
∴BC=CD,
∴∠BDC=×(180°﹣114°)=33°,
∵DB平分∠ADC,
∴∠ADB=∠BDC=33°.
30.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
一、选择题(共10小题)
1.如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )
A.100° B.80° C.50° D.40°
2.如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则的度数为何( )
A.50° B.60° C.100° D.120°
3.已知圆O的半径是4,圆心O到直线L的距离d=6,则直线L与圆O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
4.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5 cm B.8 cm C.10 cm D.12 cm
5.如图⊙O的两条弦AB、CD相交于点E,AC与DB的延长线交于点P,下列结论中成立的是( )
A.CE CD=BE BA B.CE AE=BE DE
C.PC CA=PB BD D.PC PA=PB PD
6.如图,在4×4的方格中,每个小方格都是边长为1的正方形,O、A、B分别是小正方形的顶点,则的长度为( )
A.π B. C.2π D.4π
7.已知a,b,c是△ABC三边的长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5,b=12,c=12
C.a=5,b=12,c=13 D.a=5,b=12,c=14
8.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
9.已知圆O的半径为5,P为圆O内一点,且OP=3,则过点P的所有弦中,弦长是整数的共有( )
A.4条 B.3条 C.2条 D.1条
10.如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A',再以点B为圆心,BA'为半径作圆弧交CB的延长线于B',依次进行.得到螺旋线,再顺次连接EA',AB',BC',CD',DE',得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
A. B. C. D.
二、填空题(共10小题)
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为 .
12.如图,⊙O中,弦AB、CD相交于点P,若AP=5,BP=4,CP=3,则DP为 .
13.已知AC与AB切⊙O于C、B两点,过上一点D作⊙O切线交AC于E、交AB于F,若EF⊥AB,AE=5,EF=4,则AO= .
14.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
15.如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B= 度.
16.如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 时,BP与⊙O相切.
17.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是 .
18.在△ABC中,AB=4,BC=5,AC=6,⊙O是△ABC的内切圆,则⊙O的半径为 .
19.如图,⊙O1与⊙O2交于点A,B,延长⊙O2的直径CA交⊙O1于点D,延长⊙O2的弦CB交⊙O1于点E.已知AC=6,AD:BC:BE=1:1:5,则DE的长是 .
20.如图,已知⊙O的半径为2,正方形ABCD的边长为2,过点O作OM⊥AB,垂足为M,AM=BM,若阴影部分的面积为2,则OM长为 .
三、解答题(共10小题)
21.如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
(1)求证:DE所在的直线为⊙O的切线.
(2)若AB=10,BE=5,求OF的长.
22.如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
23.如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)连接OE交⊙O于F,连接DF,若tan∠EDF=,求cos∠DEF的值.
24.如图,已知EF过圆O的圆心O,且弦AB⊥EF,连接AE交⊙O于点C,连接BC交EF于点
D,连接OB、OC.
(1)若∠E=24°,求∠BOC的度数;
(2)若OB=2,OD=1,求DE的长.
25.如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)连接OE,若OE=2,求DE的长.
26.如图,已知,BE是⊙O的直径,BC切⊙O于B,弦DE∥OC,连接CD并延长交BE的延长线于点A.
(1)证明:CD是⊙O的切线;
(2)若AD=2,AE=1,求CD的长.
27.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
28.每个小方格都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图.
(1)将菱形OABC先向右平移4个单位,再向上平移2个单位,得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2,并求出点B旋转到B2的路径长.
29.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A等于66°,求∠ADB的度数.
30.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
2021年北师大新版九年级(下)《第3章 圆》名校试题套卷(4)
参考答案与试题解析
一、选择题(共10小题)
1.如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )
A.100° B.80° C.50° D.40°
【解答】解:∵OA=OB,
∴∠BAO=∠ABO=50°,
∴∠AOB=180°﹣50°﹣50°=80°,
∴∠ACB=∠AOB=40°.
故选:D.
2.如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则的度数为何( )
A.50° B.60° C.100° D.120°
【解答】解:∵∠A=70°,∠B=60°,
∴∠C=50°.
∵此圆与直线BC相切于C点,
∴的度数=2∠C=100°.
故选:C.
3.已知圆O的半径是4,圆心O到直线L的距离d=6,则直线L与圆O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
【解答】解:根据圆心到直线的距离6大于圆的半径4,则直线和圆相离.
故选:A.
4.如图,把一个宽度为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么光盘的直径是( )
A.5 cm B.8 cm C.10 cm D.12 cm
【解答】解:设光盘的圆心为O,如图所示:
过点O作OA垂直直尺于点A,连接OB,设OB=x,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴AB=×(10﹣2)=4,
∵刻度尺宽2cm,
∴OA=x﹣2,
在Rt△OAB中,
OA2+AB2=OB2,即(x﹣2)2+42=x2,
解得:x=5.
∴该光盘的直径是10cm.
故选:C.
5.如图⊙O的两条弦AB、CD相交于点E,AC与DB的延长线交于点P,下列结论中成立的是( )
A.CE CD=BE BA B.CE AE=BE DE
C.PC CA=PB BD D.PC PA=PB PD
【解答】解:由相交弦定理知,CE ED=BE AE,由切割线定理知,PC PA=PB PD,只有D正确.
故选:D.
6.如图,在4×4的方格中,每个小方格都是边长为1的正方形,O、A、B分别是小正方形的顶点,则的长度为( )
A.π B. C.2π D.4π
【解答】解:
∵AC=OC=OD=BD=2,
∠C=∠D=90°,
∴∠AOC=∠BOD=45°,
∴∠AOB=90°,
由勾股定理得:AO=BO=2,
的长度为=,
故选:B.
7.已知a,b,c是△ABC三边的长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5,b=12,c=12
C.a=5,b=12,c=13 D.a=5,b=12,c=14
【解答】解:∵外接圆的圆心在△ABC一条边上,
∴△ABC是直角三角形.
∴当a=5,b=12,c=13时,a2+b2=c2,
则△ABC是直角三角形.
故选:C.
8.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A. B. C. D.
【解答】解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F
∵AB,AE都为圆的切线
∴AE=AB
∵OB=OE,AO=AO
∴△ABO≌△AEO(SSS)
∴∠OAB=∠OAE
∴AO⊥BE
在直角△AOB里AO2=OB2+AB2
∵OB=1,AB=3
∴AO=
易证明△BOF∽△AOB
∴BO:AO=OF:OB
∴1:=OF:1
∴OF=
sin∠CBE==
故选:D.
9.已知圆O的半径为5,P为圆O内一点,且OP=3,则过点P的所有弦中,弦长是整数的共有( )
A.4条 B.3条 C.2条 D.1条
【解答】解:如图,过P作弦AB⊥OP,交⊙O于A、B,连接OA,
Rt△OAP中,OP=3,OA=5,
根据勾股定理,得AP==4,
即由垂径定理得:AB=2AP=8,
∵最长的弦是直径,长度是10,
∴过点P的弦的长度都在8~10之间,
∴弦长为8、9、10,
当弦长为8、10时,过P点的弦分别为弦AB和过P点的直径,分别有一条;
当弦长为9时,根据圆的对称性知,符合条件的弦应该有两条;
故弦长为整数的弦共有4条,
故选:A.
10.如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A',再以点B为圆心,BA'为半径作圆弧交CB的延长线于B',依次进行.得到螺旋线,再顺次连接EA',AB',BC',CD',DE',得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
A. B. C. D.
【解答】解:设五边形的边长为a.则S1=﹣ a2 sin72°,
S2=﹣ a 2a sin72°,
S3=﹣ a 3a sin72°,
S4=﹣ a 4a sin72°,
S5=﹣ a 5a sin72°,
∵S5﹣S2=1,
∴5πa2﹣πa2﹣a2 sin72°=1,
∴ π a2﹣a2 sin72°=1,
∴S4﹣S3=πa2﹣πa2﹣a2sin72°=π a2﹣a2sin72°=,
故选:D.
二、填空题(共10小题)
11.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为 4cm或2cm .
【解答】解:当点P在圆内时,则直径=6+2=8cm,因而半径是4cm;当点P在圆外时,直径=6﹣2=4cm,因而半径是2cm.
所以⊙O的半径为4或2cm.
12.如图,⊙O中,弦AB、CD相交于点P,若AP=5,BP=4,CP=3,则DP为 .
【解答】解:由相交弦定理得,PA PB=PC PD,
∴5×4=3×DP,
解得,DP=,
故答案为:.
13.已知AC与AB切⊙O于C、B两点,过上一点D作⊙O切线交AC于E、交AB于F,若EF⊥AB,AE=5,EF=4,则AO= .
【解答】解:如图,
∵EF⊥AB,AE=5,EF=4,
∴AF2=52﹣42=9,
∴AF=3;
∵ABACEF分别是⊙O的切线,
∴AB=AC,EG=EC,FG=FB;
OC⊥EC,OG⊥GE,OB⊥FB;
∴AE+EF+AF=AC+AB=2AC=12,
∴AC=6;
在RT△EOC与RT△EOG中,
,
∴RT△EOC≌RT△EOG(HL),
同理可证:△GOF≌△BOF,
∴=4R(R为⊙O的半径),
∵,
,
∴4R+6=6R,
∴R=3,
由勾股定理得:
AO2=62+32,
∴AO=,
股改答案为.
14.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 (2,1) .
【解答】解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
15.如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B= 60 度.
【解答】解:如图,连接OA,
∵OA=OC,
∴∠OAC=∠C=20°,
∴∠OAB=60°,
∵OA=OB,
∴∠B=∠OAB=60°,
故答案为:60.
16.如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 2秒或10秒 时,BP与⊙O相切.
【解答】解:连接OP
∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=6cm,
弧AP==2π,
∵圆的周长为:12π,
∴点P运动的距离为2π或12π﹣2π=10π;
∴当t=2秒或10秒时,有BP与⊙O相切.
故答案为:2秒或10秒.
17.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是 π .
【解答】解:将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A'重合,则转过的距离是圆的周长是π,因而点A'对应的实数是π.
故答案为:π.
18.在△ABC中,AB=4,BC=5,AC=6,⊙O是△ABC的内切圆,则⊙O的半径为 .
【解答】解:设切点分别为点D,E,F,连接AO,BO,CO,OD,OF,OE,过点A作AH⊥BC于点H,
设BH=x,则CH=BC﹣x=5﹣x,
∵AH2=AB2﹣BH2,AH2=AC2﹣CE2,
∴AB2﹣BH2=AC2﹣CE2,
即16﹣x2=36﹣(5﹣x)2,
解得:x=,
∴AH=,
∴S△ABC=BC AH=,
∵⊙O是△ABC的内切圆,
∴OD⊥AB,OF⊥AC,OE⊥BC,OF=OD=OE,
∵S△ABC=S△AOB+S△BOC+S△AOC,
∴=×(AB+BC+AC)×OD,
解得:OD=,
∴⊙O的半径为,
故答案为:.
19.如图,⊙O1与⊙O2交于点A,B,延长⊙O2的直径CA交⊙O1于点D,延长⊙O2的弦CB交⊙O1于点E.已知AC=6,AD:BC:BE=1:1:5,则DE的长是 9 .
【解答】解:连接AB,在圆内接四边形ABED中,∠BAC=∠E,∠ABC=∠EDC,
因为AC为⊙O2直径,则∠ABC=90°,于是△ABC∽△EDC,
因为AD:BC:BE=1:1:5,
所以,设AD=x,BC=x,BE=5x;
于是:=,即6x2=36+6x,x2﹣x﹣6=0,
解得x=3,x=﹣2(负值舍去),
在Rt△EDC中,ED==9.
20.如图,已知⊙O的半径为2,正方形ABCD的边长为2,过点O作OM⊥AB,垂足为M,AM=BM,若阴影部分的面积为2,则OM长为 ﹣1+ .
【解答】解:设AD交⊙O于E,BC交⊙O于F,连接EF,OE,OF,延长OM交EF于H.
由题意EF∥AB,EF=AB=2,
∵OM⊥AB,
∴OH⊥EF,
∴EH=FH=1,
∴sin∠FOH==,
∴∠FOH=30°,
∵OE=OF,OH⊥EF,
∴∠EOH=∠FOH=30°,
∴∠EOF=60°,
∴OH=FH=,
∵阴影部分的面积为2,设AE=BF=MH=x,
∴2(2﹣x)﹣(﹣×22)=2,
解得x=1﹣+,
∴OM=OH﹣MH=﹣(1﹣+)=﹣1+,
故答案为﹣1+.
三、解答题(共10小题)
21.如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
(1)求证:DE所在的直线为⊙O的切线.
(2)若AB=10,BE=5,求OF的长.
【解答】(1)证明:连接OD;如图1所示:
∵O、D分别是AB、AC的中点,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOE=∠BEO;
∵OB=OE,
∴∠AOD=∠DOE,
在△OAD和△OED中,,
∴△OAD≌△OED(SAS),
∴∠OED=∠OAD=90°,DE=AD,
∴DE为⊙O的切线.
(2)解:连接AE,如图2所示:
∵AB=10,BE=5,
∴AE=5,
∴AE=AB,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠ABC=30°,
∴BC=,
∵OD∥BC,OD=BC=,
∴OD:BE=OF:EF=2:3;
∵OE=AB=5,
∴OF=2.
22.如图,已知在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证:EF的垂直平分线经过点O.
【解答】解:过点O作OG⊥CF于点G,OH⊥AE于点H,连接OF、OE,
∴由垂径定理可知:BH=AB,DG=CD,
∵AB=CD,
∴BH=DG,
∵OD=OB,
∴由勾股定理可知:OG2=OH2,
∵BE=DF,
∴BE+BH=DF+DG,
∴EH=FG,
∴在Rt△OEH与Rt△OFG中,
由勾股定理可知:OE2=OF2,
∴OE=OF,
∴△OFE是等腰三角形,
∴由等腰三角形的三线合一可知:EF的垂直平分线过O点.
23.如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)连接OE交⊙O于F,连接DF,若tan∠EDF=,求cos∠DEF的值.
【解答】解:(1)连接OD,如图,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∴OD为△ABC的中位线
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)作OM⊥DF于M,ON⊥OF于N.
∵OD=OF,OM⊥DF,
∴DM=MF,设DM=MF=a,
∵∠EDF=∠DOE,
∴tan∠DOM=tan∠EDF=,
∴OM=2a,AD=OF=a,
∵ DF OM= OF DN,
∴DN=a,
∵∠ODN+∠DON=90°,∠DON+∠OED=90°,
∴∠ODN=∠OED,
∴cos∠DEF=sin∠DON==.
24.如图,已知EF过圆O的圆心O,且弦AB⊥EF,连接AE交⊙O于点C,连接BC交EF于点
D,连接OB、OC.
(1)若∠E=24°,求∠BOC的度数;
(2)若OB=2,OD=1,求DE的长.
【解答】解:(1)∵EF⊥AB,
∴∠A+∠E=90°,
∵∠E=24°,
∴∠A=90°﹣∠E=66°,
∴∠BOC=2∠A=132°;
(2)∵OB=OC,
∴∠OCB=∠OBC,
在△OBC中,∠COB=,
∵∠E=90°﹣∠A,∠A=∠BOC,
∴∠OCB=∠E,
∵∠COD=∠EOC,
∴△COD∽△EOC,
∴,
∵OB=2,OD=1,
∴,
解得OE=4,
∴DE=OE﹣OD=3.
25.如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)连接OE,若OE=2,求DE的长.
【解答】(1)证明:∵=,
∴DA=DC
∵BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BM,
∴CD⊥AB,
∴=,
∴AD=AC,
∴AD=AC=CD,即△ACD是等边三角形;
(2)连接OE,作OG⊥AD于G,
由(1)得,∠EAB=30°,
∴AB=BE,
∴OB=BE,
由勾股定理得,(BE)2+BE2=(2)2,
解得,BE=4,
则AB=4,AE=8,
在Rt△AOG中,∠OAG=30°,OA=2,
∴AG=3,
∴AD=6,
∴DE=AE﹣AD=2.
26.如图,已知,BE是⊙O的直径,BC切⊙O于B,弦DE∥OC,连接CD并延长交BE的延长线于点A.
(1)证明:CD是⊙O的切线;
(2)若AD=2,AE=1,求CD的长.
【解答】(1)证明:连接OD,
∵ED∥OC,
∴∠COB=∠DEO,∠COD=∠EDO,
∵OD=OE,
∴∠DEO=∠EDO,
∴∠COB=∠COD,
在△BCO和△DCO中,
∴△BCO≌△DCO(SAS),
∴∠CDO=∠CBO,
∵BC为圆O的切线,
∴BC⊥OB,即∠CBO=90°,
∴∠CDO=90°,
又∵OD为圆的半径,
∴CD为圆O的切线;
(2)解:∵CD,BC分别切⊙O于D,B,
∴CD=BC,
∵AD2=AE AB,即22=1 AB,
∴AB=4,
设CD=BC=x,则AC=2+x,
∵A2C=AB2+BC2
∴(2+x)2=42+x2,
解得:x=3,
∴CD=3.
27.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.
【解答】解:过O点作半径OD⊥AB于E,如图,
∴AE=BE=AB=×8=4(m),
在Rt△AEO中,OE===3(m),
∴ED=OD﹣OE=5﹣3=2(m),
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
28.每个小方格都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图.
(1)将菱形OABC先向右平移4个单位,再向上平移2个单位,得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2,并求出点B旋转到B2的路径长.
【解答】解:(1)
根据平移的性质可知B1的坐标:(8,6)
(2)点B旋转到B2的路径就是一段弧长.
根据勾股定理得OB=
根据弧长公式得:.
29.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A等于66°,求∠ADB的度数.
【解答】(1)证明:∵DB平分∠ADC,
∴=,
∵OC⊥BD,
∴=,
∴=,
∴AB=CD;
(2)解:∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°﹣∠A=114°,
∵=,
∴BC=CD,
∴∠BDC=×(180°﹣114°)=33°,
∵DB平分∠ADC,
∴∠ADB=∠BDC=33°.
30.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
