期中复习训练 第1章丰富的图形世界2021-2022学年鲁教版(五四制)六年级数学上册(word版含答案)
文档属性
| 名称 | 期中复习训练 第1章丰富的图形世界2021-2022学年鲁教版(五四制)六年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 236.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 08:35:39 | ||
图片预览

文档简介
2021-2022学年鲁教版六年级数学上册《第1章丰富的图形世界》期中复习训练(附答案)
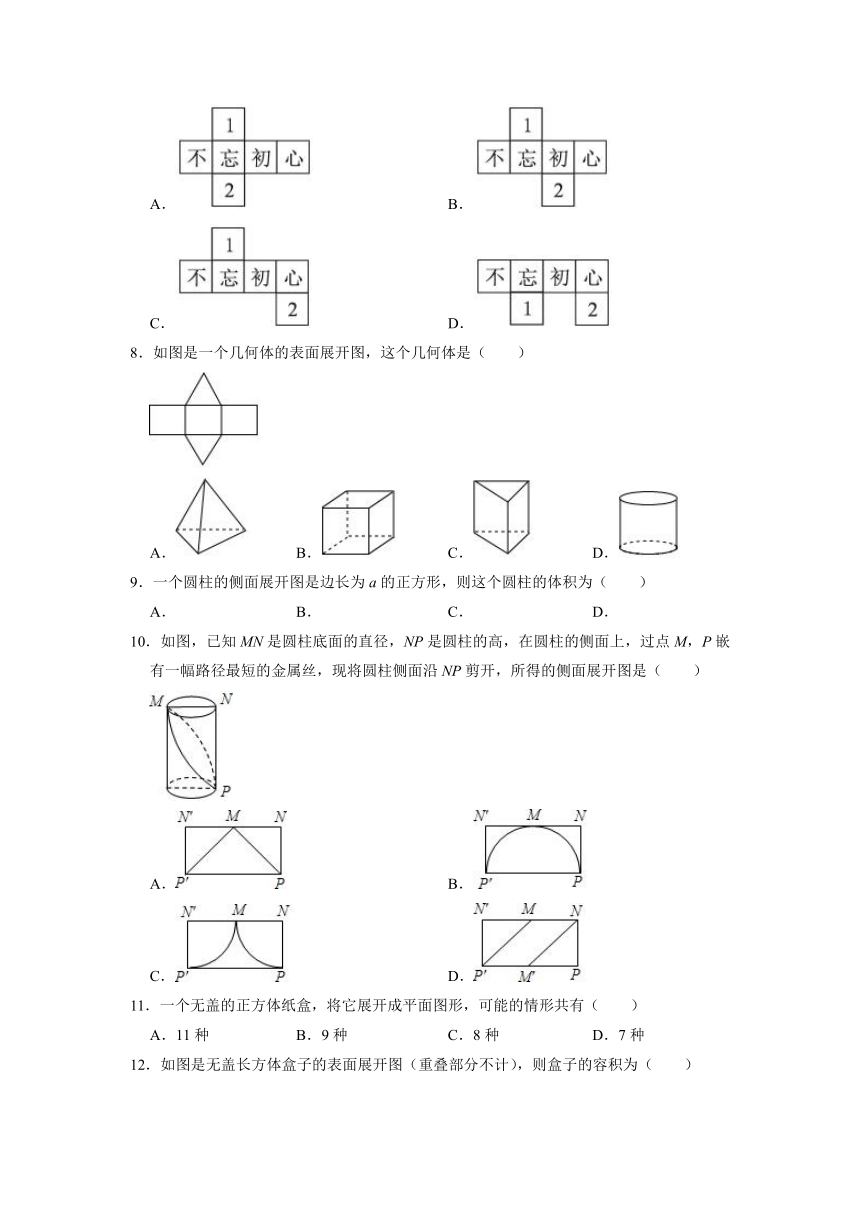
1.下列说法不正确的是( )
A.长方体与正方体都有六个面 B.圆锥的底面是圆
C.棱柱的上下底面是完全相同的图形 D.五棱柱有五个面,五条棱
2.下列几何体中,属于棱柱的有( )
A.3个 B.4个 C.5个 D.6个
3.下列四个几何体中,是四棱锥的是( )
A.B.C.D.
4.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.B.C.D.
5.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )
A. B. C. D.
6.如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A.跟 B.百 C.走 D.年
7.下列展开图中,不是正方体展开图的是( )
A. B.
C. D.
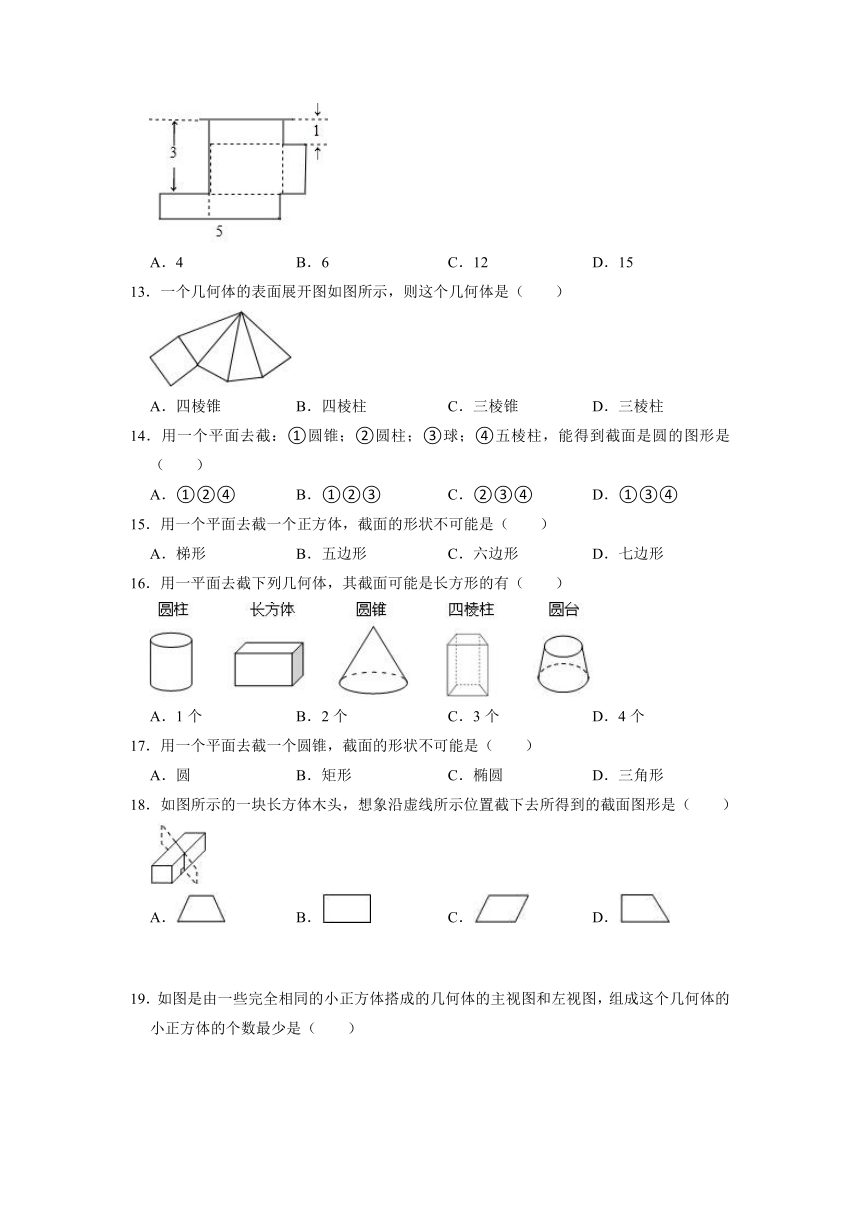
8.如图是一个几何体的表面展开图,这个几何体是( )
A. B. C. D.
9.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为( )
A. B. C. D.
10.如图,已知MN是圆柱底面的直径,NP是圆柱的高,在圆柱的侧面上,过点M,P嵌有一幅路径最短的金属丝,现将圆柱侧面沿NP剪开,所得的侧面展开图是( )
A. B.
C. D.
11.一个无盖的正方体纸盒,将它展开成平面图形,可能的情形共有( )
A.11种 B.9种 C.8种 D.7种
12.如图是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( )
A.4 B.6 C.12 D.15
13.一个几何体的表面展开图如图所示,则这个几何体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
14.用一个平面去截:①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是( )
A.①②④ B.①②③ C.②③④ D.①③④
15.用一个平面去截一个正方体,截面的形状不可能是( )
A.梯形 B.五边形 C.六边形 D.七边形
16.用一平面去截下列几何体,其截面可能是长方形的有( )
A.1个 B.2个 C.3个 D.4个
17.用一个平面去截一个圆锥,截面的形状不可能是( )
A.圆 B.矩形 C.椭圆 D.三角形
18.如图所示的一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是( )
A. B. C. D.
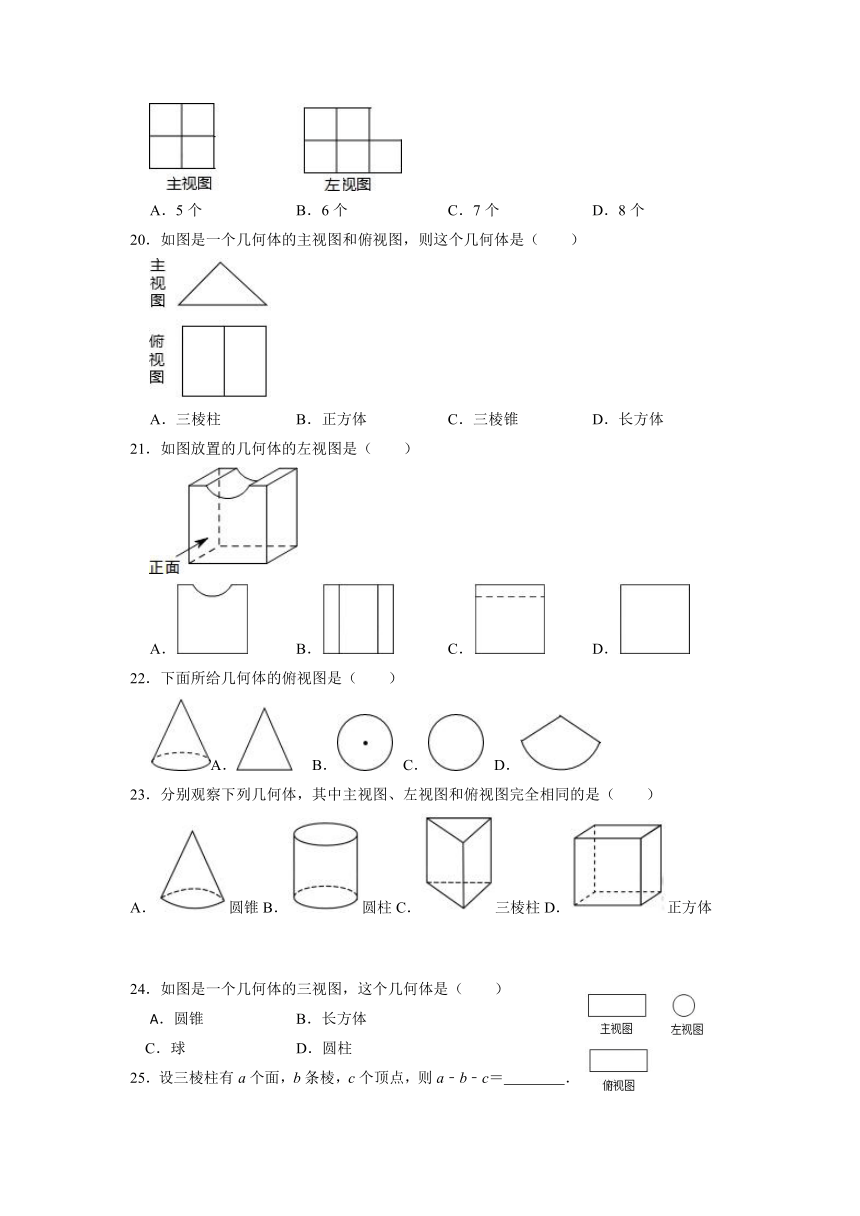
19.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )
A.5个 B.6个 C.7个 D.8个
20.如图是一个几何体的主视图和俯视图,则这个几何体是( )
A.三棱柱 B.正方体 C.三棱锥 D.长方体
21.如图放置的几何体的左视图是( )
A. B. C. D.
22.下面所给几何体的俯视图是( )
A. B. C. D.
23.分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )
A.圆锥B.圆柱C.三棱柱D.正方体
24.如图是一个几何体的三视图,这个几何体是( )
圆锥 B.长方体
C.球 D.圆柱
25.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c= .
26.一个五棱柱有 个顶点, 个面, 条棱.
27.如图,长方形的长为3cm,宽为2cm,以该长方形的一边所在直线为轴,将其旋转一周,形成圆柱,其体积为 cm3.(结果保留π)
28.夏天,汽车的雨刷能把玻璃上的雨水刷干净,这是属于“ ”的实际应用.
29.请同学们手拿一枚硬币,将其立在桌面上用力一转,它形成的是一个 体,由此说明 .
30.一个圆柱的底面直径为6cm,高为10cm,则这个圆柱的侧面积是 cm2(结果保留π).
31.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
32.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
33.把图折叠成一个正方体,如果相对面的值相等,则一组x,y的值是 .
34.如图所示,截去正方体一角变成一个多面体,这个多面体有 个面,有 条棱,有 个顶点.
35.用平面去截一个六棱柱,截面的形状最多是 边形.
36.一个由小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示,这个几何体是由 个小立方块搭成的.
37.如图,是一个食品包装盒的表面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标示的尺寸,计算这个多面体的侧面积和全面积.(侧面积与两个底面积之和)
38.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)
39.如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 个小正方体.
参考答案
1.解:A、长方体与正方体都有六个面,说法正确;
B、圆锥的底面是圆,说法正确;
C、棱柱的上下底面是完全相同的图形,说法正确;
D、五棱柱有七个面,15条棱,说法错误.
故选:D.
2.解:第一、第三、第六个几何体是棱柱,共有3个.
故选:A.
3.解:四棱锥是底面是四边形的锥体,因此选项A中的几何体符合题意,
故选:A.
4.解:绕直线l旋转一周,可以得到圆台,
故选:D.
5.解:将直角三角形绕较长直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕较短直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕斜边所在直线旋转一周后形成的几何体为:
故选:C.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,和“建”字所在面相对的面上的字是“百”.
故选:B.
7.解:选项A、B、C均能围成正方体;
选项D围成几何体时,有两个面重合,故不能围成正方体.
故选:D.
8.解:由平面图形的折叠及三棱柱的展开图的特征可知,这个几何体是三棱柱.
故选:C.
9.解:根据题意得:()2π×a=,
故选:A.
10.解:因圆柱的展开面为长方形,MP展开应该是两直线,且有公共点M.故选A.
11.解:和一个正方体的平面展开图相比较,可得出一个无盖的正方体有八种平面展开图.
故选:C.
12.解:盒子的容积为3×2×1=6.故选B.
13.解:如图所示:这个几何体是四棱锥.
故选:A.
14.解:圆锥,如果截面与底面平行,那么截面就是圆;
圆柱,如果截面与上下面平行,那么截面是圆;
球,截面一定是圆;
五棱柱,无论怎么去截,截面都不可能有弧度.
故选:B.
15.解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.
故选:D.
16.解:圆锥不可能得到长方形截面,
故能得到长方形截面的几何体有:长方体、圆柱、四棱柱一共有3个.
故选:C.
17.解:过圆锥的顶点的截面是三角形,平行于圆锥的底面的截面是圆,不平行于圆锥的底面的截面是椭圆,
截面不可能是矩形,故B符合题意;
故选:B.
18.解:长方体的截面,经过长方体四个侧面,长方体中,对边平行,故可确定为平行四边形,交点垂直于底边,故为矩形.
故选:B.
19.解:由题中所给出的主视图知物体共2列,且都是最高两层;由左视图知共两行,所以小正方体的个数最少的几何体为:第一列第一行2个小正方体,第一列第二行2个小正方体,第二列第三行1个小正方体,其余位置没有小正方体.即组成这个几何体的小正方体的个数最少为:2+2+1=5个.
故选:A.
20.解:由主视图和俯视图可得几何体为三棱柱,
故选:A.
21.解:左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
故选:C.
22.解:由几何体可得:圆锥的俯视图是圆,且有圆心.
故选:B.
23.解:圆锥的主视图、左视图都是等腰三角形,而俯视图是圆,因此选项A不符合题意;
圆柱体的主视图、左视图都是矩形,而俯视图是圆形,因此选项B不符合题意;
三棱柱主视图、左视图都是矩形,而俯视图是三角形,因此选项C不符合题意;
正方体的三视图都是形状、大小相同的正方形,因此选项D符合题意;
故选:D.
24.解:由于主视图和俯视图为长方形可得此几何体为柱体,由左视图为圆形可得为圆柱.
故选:D.
25.解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
26.解:故五棱柱有7个面,15条棱,10个顶点.
故答案为10,7,15.
27.解:由题可得,
当以该长方形的长所在直线为轴时V=π 22×3=12π,
当以该长方形的宽所在直线为轴,V=π 32×2=18π,
故答案为:12π或18π.
28.解:汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故答案为线动成面.
29.解:硬币立在桌面上用力一转,它形成的是一个球体;
从运动的观点可知,这种现象说明面动成体.
故答案为:球;面动成体.
30.解:∵一个圆柱的底面直径为6cm,高为10cm,
∴这个圆柱的侧面积是:πd×10=60π(cm2).
故答案为:60π.
31.解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,
则表面积是2×2×6=24.
故答案为:24.
32.解:①底面周长为6,高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π,高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
33.解:由图可知,面“x+y”与面“5”相对,面“xy”与面“6”相对.
根据相对面的值相等得,x+y=5且xy=6,
解得x=2,y=3或x=3,y=2.
34.解:仔细观察图形,正确地数出多面体的面数、棱数及顶点数,它们分别是7,12,7.
35.解:∵用平面去截六棱柱时最多与8个面相交得八边形,
∴最多可以截出八边形.
故答案是:八.
36.解:由俯视图易得最底层小立方块的个数为4,由其他视图可知第二层有一个小立方块,那么共有4+1=5个小立方块.
故答案为:5.
37.解:(1)根据图示可知形状为直六棱柱.
(2)S侧=6ab,S正六边形=,
S全=6ab+.
38.解:答案不唯一,如图.
39.解:(1)如图所示:
;
(2)图中共有9个小正方体.
故答案为:9.
1.下列说法不正确的是( )
A.长方体与正方体都有六个面 B.圆锥的底面是圆
C.棱柱的上下底面是完全相同的图形 D.五棱柱有五个面,五条棱
2.下列几何体中,属于棱柱的有( )
A.3个 B.4个 C.5个 D.6个
3.下列四个几何体中,是四棱锥的是( )
A.B.C.D.
4.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.B.C.D.
5.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )
A. B. C. D.
6.如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A.跟 B.百 C.走 D.年
7.下列展开图中,不是正方体展开图的是( )
A. B.
C. D.
8.如图是一个几何体的表面展开图,这个几何体是( )
A. B. C. D.
9.一个圆柱的侧面展开图是边长为a的正方形,则这个圆柱的体积为( )
A. B. C. D.
10.如图,已知MN是圆柱底面的直径,NP是圆柱的高,在圆柱的侧面上,过点M,P嵌有一幅路径最短的金属丝,现将圆柱侧面沿NP剪开,所得的侧面展开图是( )
A. B.
C. D.
11.一个无盖的正方体纸盒,将它展开成平面图形,可能的情形共有( )
A.11种 B.9种 C.8种 D.7种
12.如图是无盖长方体盒子的表面展开图(重叠部分不计),则盒子的容积为( )
A.4 B.6 C.12 D.15
13.一个几何体的表面展开图如图所示,则这个几何体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
14.用一个平面去截:①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是( )
A.①②④ B.①②③ C.②③④ D.①③④
15.用一个平面去截一个正方体,截面的形状不可能是( )
A.梯形 B.五边形 C.六边形 D.七边形
16.用一平面去截下列几何体,其截面可能是长方形的有( )
A.1个 B.2个 C.3个 D.4个
17.用一个平面去截一个圆锥,截面的形状不可能是( )
A.圆 B.矩形 C.椭圆 D.三角形
18.如图所示的一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是( )
A. B. C. D.
19.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )
A.5个 B.6个 C.7个 D.8个
20.如图是一个几何体的主视图和俯视图,则这个几何体是( )
A.三棱柱 B.正方体 C.三棱锥 D.长方体
21.如图放置的几何体的左视图是( )
A. B. C. D.
22.下面所给几何体的俯视图是( )
A. B. C. D.
23.分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )
A.圆锥B.圆柱C.三棱柱D.正方体
24.如图是一个几何体的三视图,这个几何体是( )
圆锥 B.长方体
C.球 D.圆柱
25.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c= .
26.一个五棱柱有 个顶点, 个面, 条棱.
27.如图,长方形的长为3cm,宽为2cm,以该长方形的一边所在直线为轴,将其旋转一周,形成圆柱,其体积为 cm3.(结果保留π)
28.夏天,汽车的雨刷能把玻璃上的雨水刷干净,这是属于“ ”的实际应用.
29.请同学们手拿一枚硬币,将其立在桌面上用力一转,它形成的是一个 体,由此说明 .
30.一个圆柱的底面直径为6cm,高为10cm,则这个圆柱的侧面积是 cm2(结果保留π).
31.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
32.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
33.把图折叠成一个正方体,如果相对面的值相等,则一组x,y的值是 .
34.如图所示,截去正方体一角变成一个多面体,这个多面体有 个面,有 条棱,有 个顶点.
35.用平面去截一个六棱柱,截面的形状最多是 边形.
36.一个由小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示,这个几何体是由 个小立方块搭成的.
37.如图,是一个食品包装盒的表面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标示的尺寸,计算这个多面体的侧面积和全面积.(侧面积与两个底面积之和)
38.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)
39.如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 个小正方体.
参考答案
1.解:A、长方体与正方体都有六个面,说法正确;
B、圆锥的底面是圆,说法正确;
C、棱柱的上下底面是完全相同的图形,说法正确;
D、五棱柱有七个面,15条棱,说法错误.
故选:D.
2.解:第一、第三、第六个几何体是棱柱,共有3个.
故选:A.
3.解:四棱锥是底面是四边形的锥体,因此选项A中的几何体符合题意,
故选:A.
4.解:绕直线l旋转一周,可以得到圆台,
故选:D.
5.解:将直角三角形绕较长直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕较短直角边所在直线旋转一周后形成的几何体为:
将直角三角形绕斜边所在直线旋转一周后形成的几何体为:
故选:C.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,和“建”字所在面相对的面上的字是“百”.
故选:B.
7.解:选项A、B、C均能围成正方体;
选项D围成几何体时,有两个面重合,故不能围成正方体.
故选:D.
8.解:由平面图形的折叠及三棱柱的展开图的特征可知,这个几何体是三棱柱.
故选:C.
9.解:根据题意得:()2π×a=,
故选:A.
10.解:因圆柱的展开面为长方形,MP展开应该是两直线,且有公共点M.故选A.
11.解:和一个正方体的平面展开图相比较,可得出一个无盖的正方体有八种平面展开图.
故选:C.
12.解:盒子的容积为3×2×1=6.故选B.
13.解:如图所示:这个几何体是四棱锥.
故选:A.
14.解:圆锥,如果截面与底面平行,那么截面就是圆;
圆柱,如果截面与上下面平行,那么截面是圆;
球,截面一定是圆;
五棱柱,无论怎么去截,截面都不可能有弧度.
故选:B.
15.解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.
故选:D.
16.解:圆锥不可能得到长方形截面,
故能得到长方形截面的几何体有:长方体、圆柱、四棱柱一共有3个.
故选:C.
17.解:过圆锥的顶点的截面是三角形,平行于圆锥的底面的截面是圆,不平行于圆锥的底面的截面是椭圆,
截面不可能是矩形,故B符合题意;
故选:B.
18.解:长方体的截面,经过长方体四个侧面,长方体中,对边平行,故可确定为平行四边形,交点垂直于底边,故为矩形.
故选:B.
19.解:由题中所给出的主视图知物体共2列,且都是最高两层;由左视图知共两行,所以小正方体的个数最少的几何体为:第一列第一行2个小正方体,第一列第二行2个小正方体,第二列第三行1个小正方体,其余位置没有小正方体.即组成这个几何体的小正方体的个数最少为:2+2+1=5个.
故选:A.
20.解:由主视图和俯视图可得几何体为三棱柱,
故选:A.
21.解:左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
故选:C.
22.解:由几何体可得:圆锥的俯视图是圆,且有圆心.
故选:B.
23.解:圆锥的主视图、左视图都是等腰三角形,而俯视图是圆,因此选项A不符合题意;
圆柱体的主视图、左视图都是矩形,而俯视图是圆形,因此选项B不符合题意;
三棱柱主视图、左视图都是矩形,而俯视图是三角形,因此选项C不符合题意;
正方体的三视图都是形状、大小相同的正方形,因此选项D符合题意;
故选:D.
24.解:由于主视图和俯视图为长方形可得此几何体为柱体,由左视图为圆形可得为圆柱.
故选:D.
25.解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
26.解:故五棱柱有7个面,15条棱,10个顶点.
故答案为10,7,15.
27.解:由题可得,
当以该长方形的长所在直线为轴时V=π 22×3=12π,
当以该长方形的宽所在直线为轴,V=π 32×2=18π,
故答案为:12π或18π.
28.解:汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故答案为线动成面.
29.解:硬币立在桌面上用力一转,它形成的是一个球体;
从运动的观点可知,这种现象说明面动成体.
故答案为:球;面动成体.
30.解:∵一个圆柱的底面直径为6cm,高为10cm,
∴这个圆柱的侧面积是:πd×10=60π(cm2).
故答案为:60π.
31.解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,
则表面积是2×2×6=24.
故答案为:24.
32.解:①底面周长为6,高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π,高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
33.解:由图可知,面“x+y”与面“5”相对,面“xy”与面“6”相对.
根据相对面的值相等得,x+y=5且xy=6,
解得x=2,y=3或x=3,y=2.
34.解:仔细观察图形,正确地数出多面体的面数、棱数及顶点数,它们分别是7,12,7.
35.解:∵用平面去截六棱柱时最多与8个面相交得八边形,
∴最多可以截出八边形.
故答案是:八.
36.解:由俯视图易得最底层小立方块的个数为4,由其他视图可知第二层有一个小立方块,那么共有4+1=5个小立方块.
故答案为:5.
37.解:(1)根据图示可知形状为直六棱柱.
(2)S侧=6ab,S正六边形=,
S全=6ab+.
38.解:答案不唯一,如图.
39.解:(1)如图所示:
;
(2)图中共有9个小正方体.
故答案为:9.
