期中复习综合训练 第3章勾股定理 2021-2022学年鲁教版(五四制)七年级数学上册(word版含答案)
文档属性
| 名称 | 期中复习综合训练 第3章勾股定理 2021-2022学年鲁教版(五四制)七年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 241.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 08:43:20 | ||
图片预览



文档简介
2021-2022学年鲁教版七年级数学上册《第3章勾股定理》期中复习综合训练(附答案)
1.如图,字母B所代表的正方形的边长是( )
A.306cm B.144cm C.15cm D.12cm
2.已知a、b、c分别为△ABC中∠A、∠B、∠C的对边,下列说法错误的是( )
A.∠C=90°,则a2+b2=c2 B.∠B=90°,则a2+c2=b2
C.∠A=90°,则b2+c2=a2 D.总有a2+b2=c2
3.直角三角形的两条直角边分别为5cm,12cm,则斜边上的高是( )cm.
A.6 B.8 C. D.
4.如图,由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和直角边长分别是13,12.则图中阴影部分的面积是( )
A.16 B.25 C.144 D.169
5.已知一直角三角形,三边的平方和为800cm2,则斜边长为( )
A.20cm B.40cm C.400cm D.不能确定
6.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,AH=6,那么EF等于( )
A.8 B.6 C.4 D.2
7.若一个直角三角形的三边长分别为a,b,c,且a2=9,b2=16,则c2为( )
A.25 B.7 C.7或25 D.9或16
8.下列各组数中,不是勾股数的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.4,5,6
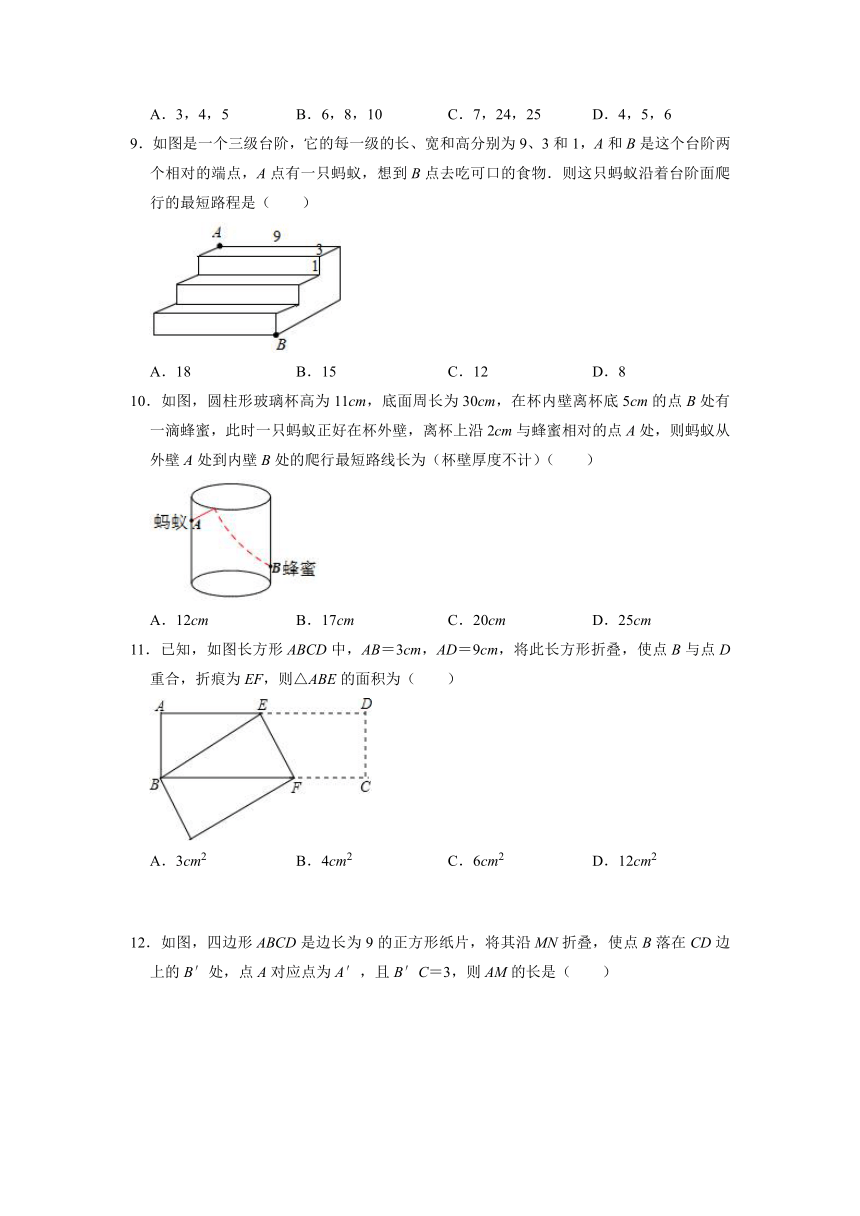
9.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是( )
A.18 B.15 C.12 D.8
10.如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的爬行最短路线长为(杯壁厚度不计)( )
A.12cm B.17cm C.20cm D.25cm
11.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
12.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,且B′C=3,则AM的长是( )
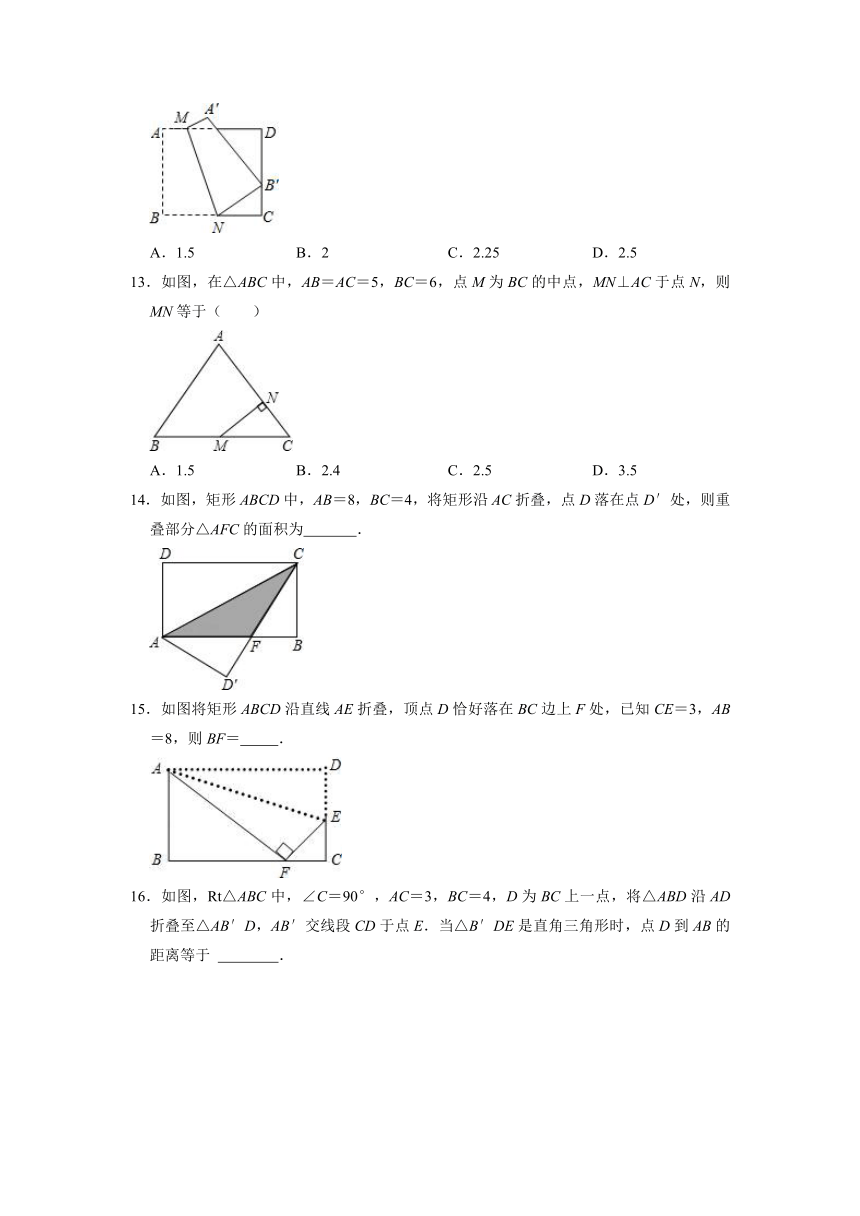
A.1.5 B.2 C.2.25 D.2.5
13.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5 B.2.4 C.2.5 D.3.5
14.如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为 .
15.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= .
16.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,D为BC上一点,将△ABD沿AD折叠至△AB′D,AB′交线段CD于点E.当△B′DE是直角三角形时,点D到AB的距离等于 .
17.如图,长方形纸片ABCD,沿折痕AE折叠边AD,使点D落在BC边上的点F处,已知AB=8,S△ABF=24,则EC的长为 .
18.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
19.如图,A,B,H是直线上的三个点,AC⊥l于点A,BD⊥l于点B,HC=HD,AB=5,AC=2,BD=3,求AH的长.
20.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
21.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以4cm/s的速度沿AC﹣CB﹣BA运动设运动时间为t秒(t>0).
(1)若点P在AC上运动,当t的值为多少时,PA=PB.
(2)若点P恰好在∠BAC的平分线上,求t的值.
参考答案与
1.解:在Rt△DEF中,由勾股定理得,DF2+EF2=DE2,
∴字母B所代表的正方形的面积=EF2=DE2﹣DF2=225﹣81=144(cm2),
∴字母B所代表的正方形的边长=12(cm),
故选:D.
2.解:选项A:∠C=90°,则c为△ABC中斜边,a,b为直角边,由勾股定理可得:
a2+b2=c2,故A正确,不符合题意;
同理可得,选项B和选项C正确,故选项B和选项C不符合题意;
选项D:只有直角三角形,且∠C为直角时,a2+b2=c2,故D错误,符合题意.
故选:D.
3.解:∵直角三角形的两条直角边分别为5cm,12cm,
∴斜边长是=13(cm),
设斜边上的高是xcm,
则,
解得x=,
故选:D.
4.解:
根据勾股定理得出:AB===5,
∴EF=AB=5,
∴阴影部分面积是EP2+PF2=25,
故选:B.
5.解:设直角三角形的两条直角边分别为acm、bcm,斜边为ccm.
根据题意,得a2+b2+c2=800,
∵a2+b2=c2,
∴2c2=800,
∴c2=400,
∵c>0,
∴(cm).
故选:A.
6.解:∵△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,
∴AH=DE=6,AD=AB=10,
在Rt△ADE中,
AE===8,
∴HE=AE﹣AH=8﹣6=2,
∵四边形EFGH是正方形,
∴EF=HE=2,
故选:D.
7.解;当a,b为直角边时,c2=a2+b2=9+16=25,
当a,c为直角边,b为斜边时,c2=b2﹣a2=16﹣9=7,
故选:C.
8.解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;
B、62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;
C、72+242=252,是正整数,故是勾股数,此选项不符合题意;
D、42+52≠62,不是勾股数,此选项符合题意.
故选:D.
9.解:将台阶展开,如图,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
故选:B.
10.解:如图:
将杯子侧面展开,
作A关于EF的对称点A′,
则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,
∵A′B====17(cm),
∴蚂蚁从外壁A处到内壁B处的最短距离为17cm,
故选:B.
11.解:将此长方形折叠,使点B与点D重合,∴BE=ED.
∵AD=9cm=AE+DE=AE+BE.
∴BE=9﹣AE,
根据勾股定理可知AB2+AE2=BE2.
解得AE=4.
∴△ABE的面积为3×4÷2=6.故选:C.
12.解:设AM=x,
连接BM,MB′,
在Rt△ABM中,AB2+AM2=BM2,
在Rt△MDB′中,B′M2=MD2+DB′2,
∵MB=MB′,
∴AB2+AM2=BM2=B′M2=MD2+DB′2,
即92+x2=(9﹣x)2+(9﹣3)2,
解得x=2,
即AM=2,
故选:B.
13.解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN AC=AM MC,
∴MN===2.4.
故选:B.
14.解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8﹣x,
在Rt△AFD′中,(8﹣x)2=x2+42,
解之得:x=3,
∴AF=AB﹣FB=8﹣3=5,
∴S△AFC= AF BC=10.
故答案为:10.
15.解:由折叠的性质知:AD=AF,DE=EF=8﹣3=5;
在Rt△CEF中,EF=DE=5,CE=3,由勾股定理可得:CF=4,
若设AD=AF=x,则BC=x,BF=x﹣4;
在Rt△ABF中,由勾股定理可得:
82+(x﹣4)2=x2,解得x=10,
故BF=x﹣4=6.
故答案为:6.
16.解:
设C点落在AB上的点为C',
∵∠C=90°,AC=3,BC=4,
∴AB=,
由折叠的性质得,AC=AC',CD=DC',∠C=∠AC'D=90°,
在△BC'D中,设DC'=x,则BD=4﹣x,BC'=5﹣3=2,
由勾股定理得,x2+22=(4﹣x)2,
解得:x=1.5,
∴BD=4﹣1.5=2.5,
故答案为:2.5.
17.解:∵AB=8,S△ABF=24
∴BF=6
在Rt△ABF中,AF==10
∴AD=AF=BC=10
∴CF=10﹣6=4
设EC=x,则EF=DE=8﹣x
在Rt△ECF中,(8﹣x)2=x2+42
解之得,x=3;故应填3.
18.解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
AO==2.4(米),
∴MO=AO﹣AM=2.4﹣0.4=2(米),
在Rt△MNO中,由勾股定理得:
NO==1.5(米),
∴NB=ON﹣OB=1.5﹣0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
19.解:∵AC⊥l于点A,BD⊥l于点B,
∴∠CAH=∠HBD=90°,
∵A,B,H是直线上的三个点,
∴AH+BH=AB=5,
∴BH=5﹣AH,
在Rt△ACH中,AC2+AH2=CH2,
即4+AH2=CH2,
在Rt△BHD中,BH2+BD2=DH2,
即(5﹣AH)2+9=DH2,
∵HC=HD,
∴4+AH2=(5﹣AH)2+9,
∴AH=3,
故AH的长为3.
20.解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,
△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.
∴x=(cm).
21.解:(1)如图1,连接BP,
在Rt△ABC中,AB=10cm,BC=6cm,
∴AC===8(cm),
则PC=8﹣PA,
由勾股定理得,PB2=PC2+BC2,
当PA=PB时,PA2=(8﹣PA)2+62,
解得,PA=,
则t=÷4=;
(2)如图2,作PG⊥AB于G,
∵点P恰好在∠BAC的角平分线上,∠C=90°,PG⊥AB,
∴CP=GP,
∴△ACP≌△AGP(HL),
∴AG=AC=8(cm),
∴BG=10﹣8=2(cm),
设CP=xcm,则BP=(6﹣x)cm,PG=xcm,
∴Rt△BGP中,BG2+PG2=BP2,即22+x2=(6﹣x)2
解得,x=,
∴AC+CP=(cm),
∴t=÷4=,
当点P沿折线A﹣C﹣B﹣A运动到点A时,点P也在∠BAC的角平分线上,
此时,t=(10+8+6)÷4=6,
综上所述,若点P恰好在∠BAC的角平分线上,t的值为或6;
1.如图,字母B所代表的正方形的边长是( )
A.306cm B.144cm C.15cm D.12cm
2.已知a、b、c分别为△ABC中∠A、∠B、∠C的对边,下列说法错误的是( )
A.∠C=90°,则a2+b2=c2 B.∠B=90°,则a2+c2=b2
C.∠A=90°,则b2+c2=a2 D.总有a2+b2=c2
3.直角三角形的两条直角边分别为5cm,12cm,则斜边上的高是( )cm.
A.6 B.8 C. D.
4.如图,由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和直角边长分别是13,12.则图中阴影部分的面积是( )
A.16 B.25 C.144 D.169
5.已知一直角三角形,三边的平方和为800cm2,则斜边长为( )
A.20cm B.40cm C.400cm D.不能确定
6.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,AH=6,那么EF等于( )
A.8 B.6 C.4 D.2
7.若一个直角三角形的三边长分别为a,b,c,且a2=9,b2=16,则c2为( )
A.25 B.7 C.7或25 D.9或16
8.下列各组数中,不是勾股数的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.4,5,6
9.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是( )
A.18 B.15 C.12 D.8
10.如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的爬行最短路线长为(杯壁厚度不计)( )
A.12cm B.17cm C.20cm D.25cm
11.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
12.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,且B′C=3,则AM的长是( )
A.1.5 B.2 C.2.25 D.2.5
13.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5 B.2.4 C.2.5 D.3.5
14.如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为 .
15.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= .
16.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,D为BC上一点,将△ABD沿AD折叠至△AB′D,AB′交线段CD于点E.当△B′DE是直角三角形时,点D到AB的距离等于 .
17.如图,长方形纸片ABCD,沿折痕AE折叠边AD,使点D落在BC边上的点F处,已知AB=8,S△ABF=24,则EC的长为 .
18.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
19.如图,A,B,H是直线上的三个点,AC⊥l于点A,BD⊥l于点B,HC=HD,AB=5,AC=2,BD=3,求AH的长.
20.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
21.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以4cm/s的速度沿AC﹣CB﹣BA运动设运动时间为t秒(t>0).
(1)若点P在AC上运动,当t的值为多少时,PA=PB.
(2)若点P恰好在∠BAC的平分线上,求t的值.
参考答案与
1.解:在Rt△DEF中,由勾股定理得,DF2+EF2=DE2,
∴字母B所代表的正方形的面积=EF2=DE2﹣DF2=225﹣81=144(cm2),
∴字母B所代表的正方形的边长=12(cm),
故选:D.
2.解:选项A:∠C=90°,则c为△ABC中斜边,a,b为直角边,由勾股定理可得:
a2+b2=c2,故A正确,不符合题意;
同理可得,选项B和选项C正确,故选项B和选项C不符合题意;
选项D:只有直角三角形,且∠C为直角时,a2+b2=c2,故D错误,符合题意.
故选:D.
3.解:∵直角三角形的两条直角边分别为5cm,12cm,
∴斜边长是=13(cm),
设斜边上的高是xcm,
则,
解得x=,
故选:D.
4.解:
根据勾股定理得出:AB===5,
∴EF=AB=5,
∴阴影部分面积是EP2+PF2=25,
故选:B.
5.解:设直角三角形的两条直角边分别为acm、bcm,斜边为ccm.
根据题意,得a2+b2+c2=800,
∵a2+b2=c2,
∴2c2=800,
∴c2=400,
∵c>0,
∴(cm).
故选:A.
6.解:∵△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,
∴AH=DE=6,AD=AB=10,
在Rt△ADE中,
AE===8,
∴HE=AE﹣AH=8﹣6=2,
∵四边形EFGH是正方形,
∴EF=HE=2,
故选:D.
7.解;当a,b为直角边时,c2=a2+b2=9+16=25,
当a,c为直角边,b为斜边时,c2=b2﹣a2=16﹣9=7,
故选:C.
8.解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;
B、62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;
C、72+242=252,是正整数,故是勾股数,此选项不符合题意;
D、42+52≠62,不是勾股数,此选项符合题意.
故选:D.
9.解:将台阶展开,如图,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
故选:B.
10.解:如图:
将杯子侧面展开,
作A关于EF的对称点A′,
则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,
∵A′B====17(cm),
∴蚂蚁从外壁A处到内壁B处的最短距离为17cm,
故选:B.
11.解:将此长方形折叠,使点B与点D重合,∴BE=ED.
∵AD=9cm=AE+DE=AE+BE.
∴BE=9﹣AE,
根据勾股定理可知AB2+AE2=BE2.
解得AE=4.
∴△ABE的面积为3×4÷2=6.故选:C.
12.解:设AM=x,
连接BM,MB′,
在Rt△ABM中,AB2+AM2=BM2,
在Rt△MDB′中,B′M2=MD2+DB′2,
∵MB=MB′,
∴AB2+AM2=BM2=B′M2=MD2+DB′2,
即92+x2=(9﹣x)2+(9﹣3)2,
解得x=2,
即AM=2,
故选:B.
13.解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN AC=AM MC,
∴MN===2.4.
故选:B.
14.解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8﹣x,
在Rt△AFD′中,(8﹣x)2=x2+42,
解之得:x=3,
∴AF=AB﹣FB=8﹣3=5,
∴S△AFC= AF BC=10.
故答案为:10.
15.解:由折叠的性质知:AD=AF,DE=EF=8﹣3=5;
在Rt△CEF中,EF=DE=5,CE=3,由勾股定理可得:CF=4,
若设AD=AF=x,则BC=x,BF=x﹣4;
在Rt△ABF中,由勾股定理可得:
82+(x﹣4)2=x2,解得x=10,
故BF=x﹣4=6.
故答案为:6.
16.解:
设C点落在AB上的点为C',
∵∠C=90°,AC=3,BC=4,
∴AB=,
由折叠的性质得,AC=AC',CD=DC',∠C=∠AC'D=90°,
在△BC'D中,设DC'=x,则BD=4﹣x,BC'=5﹣3=2,
由勾股定理得,x2+22=(4﹣x)2,
解得:x=1.5,
∴BD=4﹣1.5=2.5,
故答案为:2.5.
17.解:∵AB=8,S△ABF=24
∴BF=6
在Rt△ABF中,AF==10
∴AD=AF=BC=10
∴CF=10﹣6=4
设EC=x,则EF=DE=8﹣x
在Rt△ECF中,(8﹣x)2=x2+42
解之得,x=3;故应填3.
18.解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
AO==2.4(米),
∴MO=AO﹣AM=2.4﹣0.4=2(米),
在Rt△MNO中,由勾股定理得:
NO==1.5(米),
∴NB=ON﹣OB=1.5﹣0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
19.解:∵AC⊥l于点A,BD⊥l于点B,
∴∠CAH=∠HBD=90°,
∵A,B,H是直线上的三个点,
∴AH+BH=AB=5,
∴BH=5﹣AH,
在Rt△ACH中,AC2+AH2=CH2,
即4+AH2=CH2,
在Rt△BHD中,BH2+BD2=DH2,
即(5﹣AH)2+9=DH2,
∵HC=HD,
∴4+AH2=(5﹣AH)2+9,
∴AH=3,
故AH的长为3.
20.解:设DE=xcm,则BE=DE=x,AE=AB﹣BE=10﹣x,
△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.
∴x=(cm).
21.解:(1)如图1,连接BP,
在Rt△ABC中,AB=10cm,BC=6cm,
∴AC===8(cm),
则PC=8﹣PA,
由勾股定理得,PB2=PC2+BC2,
当PA=PB时,PA2=(8﹣PA)2+62,
解得,PA=,
则t=÷4=;
(2)如图2,作PG⊥AB于G,
∵点P恰好在∠BAC的角平分线上,∠C=90°,PG⊥AB,
∴CP=GP,
∴△ACP≌△AGP(HL),
∴AG=AC=8(cm),
∴BG=10﹣8=2(cm),
设CP=xcm,则BP=(6﹣x)cm,PG=xcm,
∴Rt△BGP中,BG2+PG2=BP2,即22+x2=(6﹣x)2
解得,x=,
∴AC+CP=(cm),
∴t=÷4=,
当点P沿折线A﹣C﹣B﹣A运动到点A时,点P也在∠BAC的角平分线上,
此时,t=(10+8+6)÷4=6,
综上所述,若点P恰好在∠BAC的角平分线上,t的值为或6;
