《第五章 平行四边形》单元测试题(含答案)
文档属性
| 名称 | 《第五章 平行四边形》单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 09:06:27 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
《第五章 平行四边形》单元测试题
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.下列说法属于平行四边形判定方法的有( )
①两组对边分别平行的四边形是平行四边形;
②平行四边形的对角线互相平分;
③两组对边分别相等的四边形是平行四边形;
④平行四边形的每组对边平行且相等;
⑤两条对角线互相平分的四边形是平行四边形
A.5个 B.4个 C.3个 D.2个
2.若n边形的内角和是它外角和的3倍,则n等于( )
A.6 B.7 C.8 D.9
3.在平行四边形ABCD中,若∠A+∠C=120°,则∠C的度数是( )
A.120° B.30° C.60° D.90°
4.如图所示,在平行四边形ABCD中,AC和BD相交于点O,AB⊥AC,∠ABD=30°,AC=2cm,则平行四边形ABCD的周长是( )
A.2()cm B.4cm C.2(-)cm D.2(2+)cm
5.如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=50°,∠BAC=80°,则∠1的度数为( )
A.60° B.50° C.40° D.25°
第5题图 第6题图
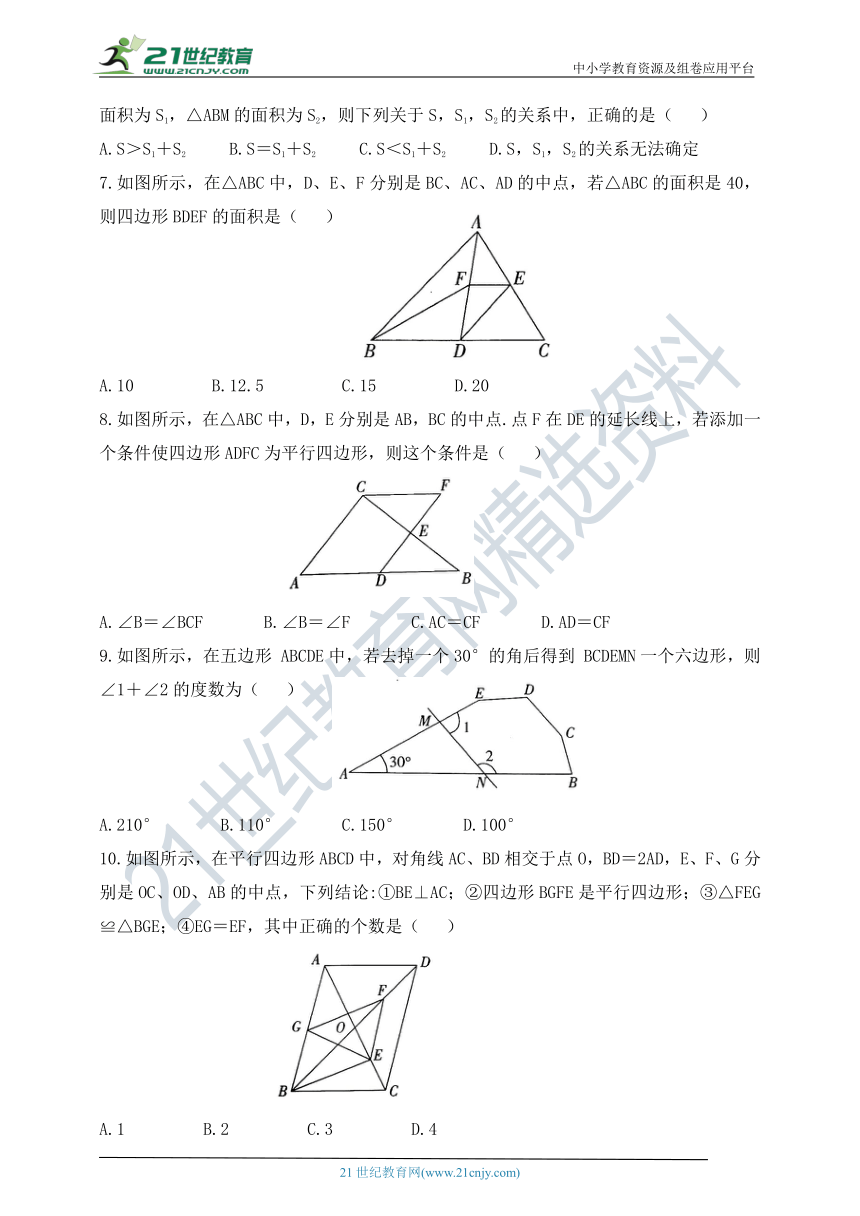
6.如图所示,M是平行四边形ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S1,△ABM的面积为S2,则下列关于S,S1,S2的关系中,正确的是( )
A.S>S1+S2 B.S=S1+S2 C.S<S1+S2 D.S,S1,S2的关系无法确定
7.如图所示,在△ABC中,D、E、F分别是BC、AC、AD的中点,若△ABC的面积是40,则四边形BDEF的面积是( )
A.10 B.12.5 C.15 D.20
8.如图所示,在△ABC中,D,E分别是AB,BC的中点.点F在DE的延长线上,若添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠BCF B.∠B=∠F C.AC=CF D.AD=CF
9.如图所示,在五边形 ABCDE中,若去掉一个30°的角后得到 BCDEMN一个六边形,则∠1+∠2的度数为( )
A.210° B.110° C.150° D.100°
10.如图所示,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②四边形BGFE是平行四边形;③△FEG≌△BGE;④EG=EF,其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
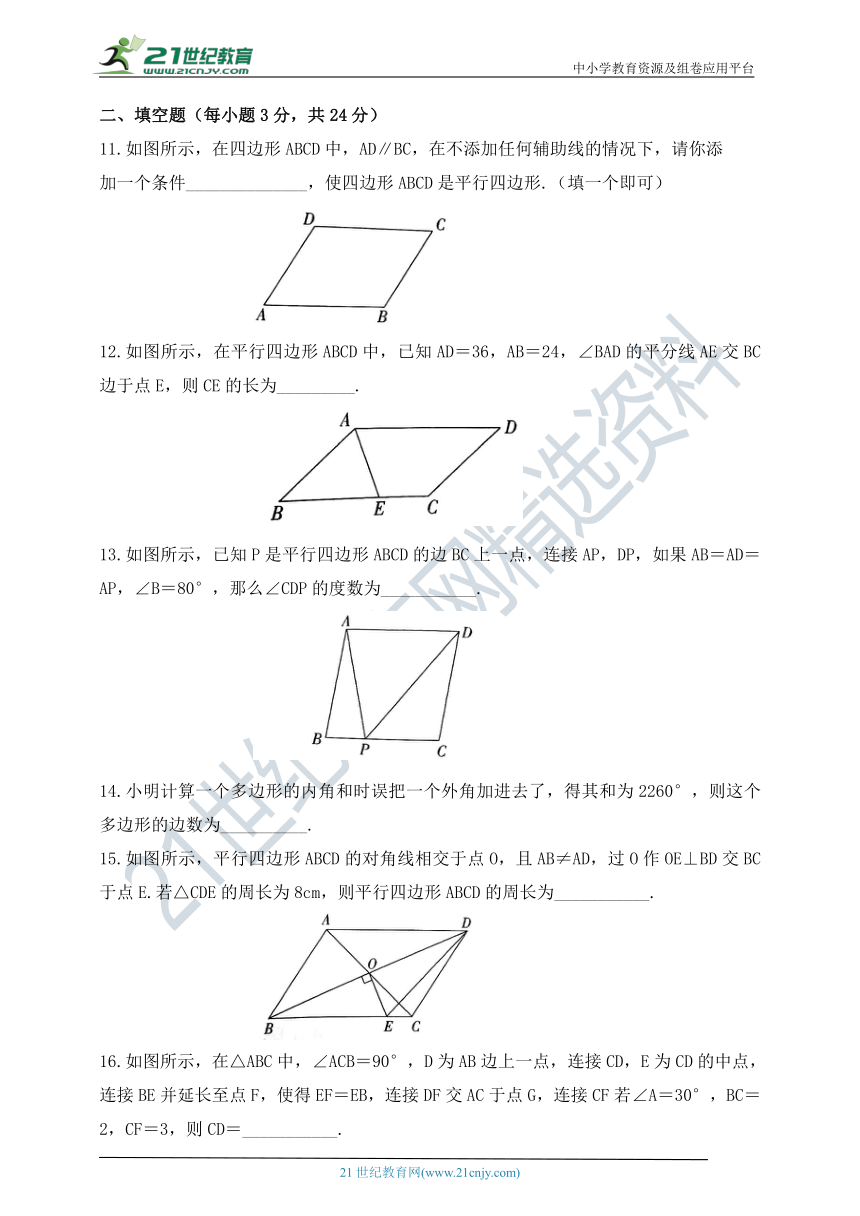
11.如图所示,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添
加一个条件______________,使四边形ABCD是平行四边形.(填一个即可)
12.如图所示,在平行四边形ABCD中,已知AD=36,AB=24,∠BAD的平分线AE交BC边于点E,则CE的长为_________.
13.如图所示,已知P是平行四边形ABCD的边BC上一点,连接AP,DP,如果AB=AD=AP,∠B=80°,那么∠CDP的度数为___________.
14.小明计算一个多边形的内角和时误把一个外角加进去了,得其和为2260°,则这个多边形的边数为__________.
15.如图所示,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则平行四边形ABCD的周长为___________.
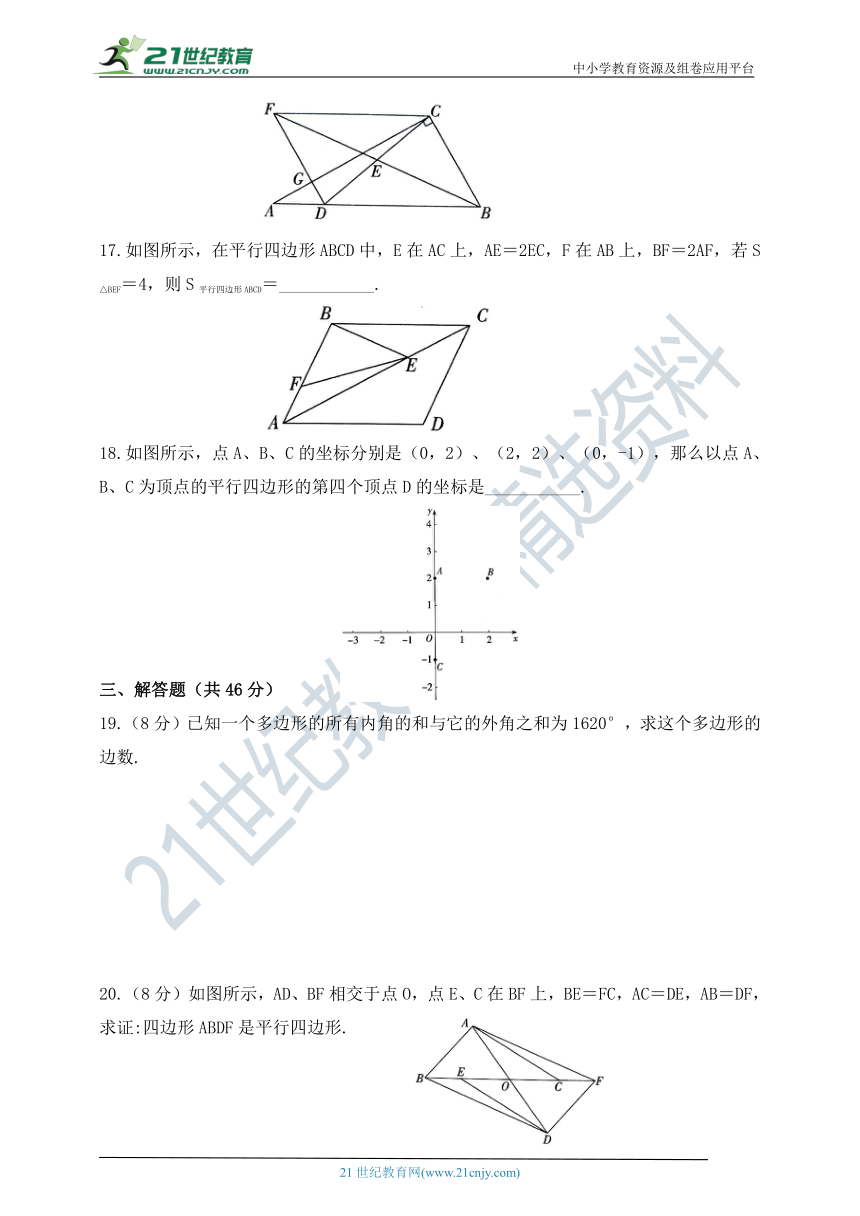
16.如图所示,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF若∠A=30°,BC=2,CF=3,则CD=___________.
17.如图所示,在平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,若S△BEF=4,则S平行四边形ABCD=___________.
18.如图所示,点A、B、C的坐标分别是(0,2)、(2,2)、(0,-1),那么以点A、B、C为顶点的平行四边形的第四个顶点D的坐标是___________.
三、解答题(共46分)
19.(8分)已知一个多边形的所有内角的和与它的外角之和为1620°,求这个多边形的边数.
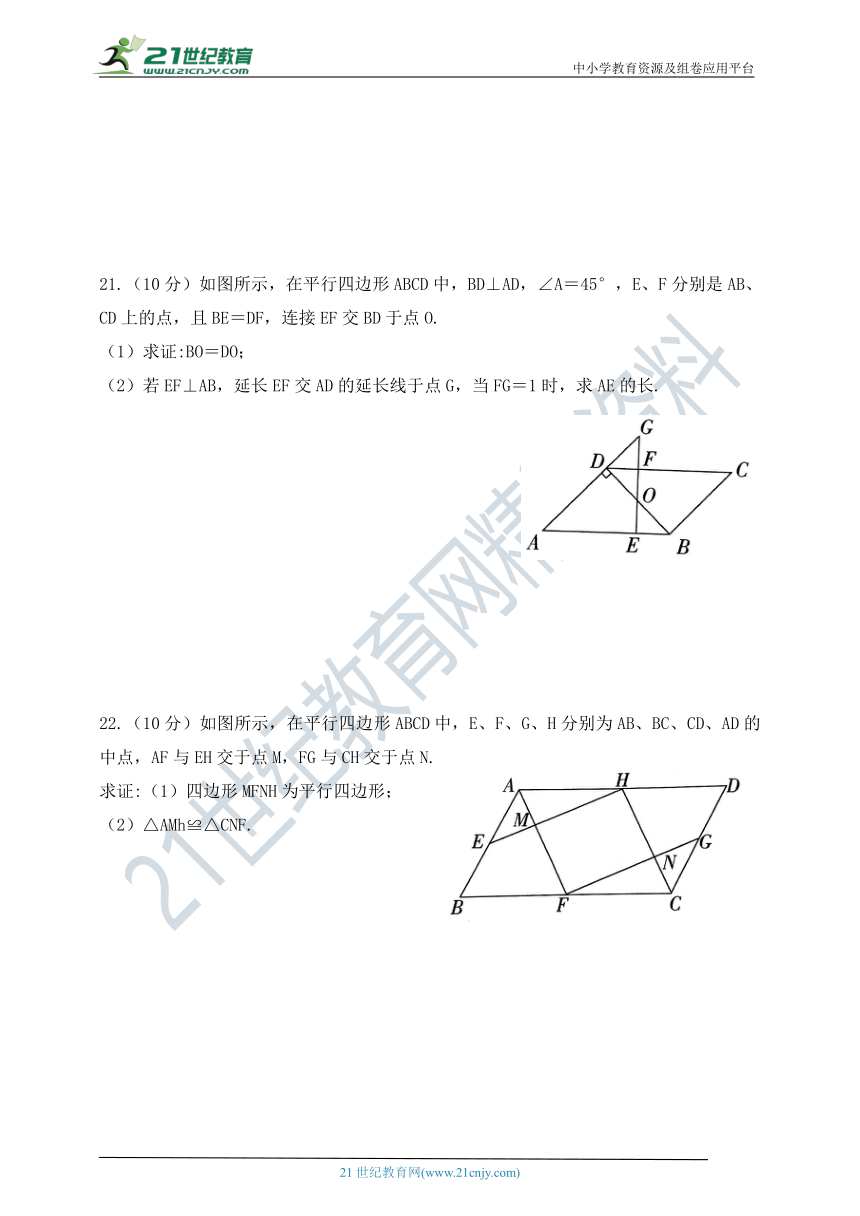
20.(8分)如图所示,AD、BF相交于点O,点E、C在BF上,BE=FC,AC=DE,AB=DF,求证:四边形ABDF是平行四边形.
21.(10分)如图所示,在平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AE的长.
22.(10分)如图所示,在平行四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
求证:(1)四边形MFNH为平行四边形;
(2)△AMh≌△CNF.
23.(10分)在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC;
(2)当点D在边BC的延长线上时,如图②.当点D在边BC的反向延长线上时,如图③.
请分别写出图②③中DE、DF、AC之间的等量关系式(不需要证明);
(3)若AC=10,DE=7,问DF的长为多少?
参考答案
一、选择题
1.C 2.C 3.C 4.A 5.B 6.B 7.C 8.A 9.A 10.D
二、填空题
11.AB∥CD(答案不唯一) 12. 12 13. 30° 14. 14 15. 16 cm
16. 17. 18 18. (-2,-1)或(2,-1)或(2,5)
三、解答题
19.解析 设这个多边形的边数是n.
由题意得(n-2)·180°+360°=1620°,解得n=9.
答:这个多边形的边数n是9.
20.证明 ∵BE=CF,∴BE+CE=CF+CE,即BC=FE.
在△ABC和△DFE中,∴△ABC≌△DFE(SSS),
∴∠ABF=∠DFE,∴AB∥DF,
又∵AB=DF,∴四边形ABDF是平行四边形.
21.解析 (1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.
在△OBE与△ODF中,∠OBE=∠ODF,∠BOE=∠DOF,BE=DF,
∴△OBE≌△ODF(AAS),∴BO=DO.
(2)∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.
∵∠A=45°,∴∠G=∠A=45°,∴AE=GE.
∵BD⊥AD,∴∠ADB=∠GDO=90°,∴∠GOD=∠G=45°,
∴DG=DO,易知EF⊥CD,∴OF=FG=1.
由(1)可知△OBE≌△ODF,∴OE=OF=1,
∴GE=OE+OF+FG=3,∴AE=3.
22.证明 (1)连接BD(图略),
∵E、H分别为AB、AD的中点,∴EH为△ABD的中位线,∴EH∥BD.
同理FG∥BD.∴EH∥FG.
在平行四边形ABCD中,AD∥BC,AD=BC,
∵H为AD的中点,∴AH=AD,∵F为BC的中点,∴FC=BC,∴AH=FC,
又∵AH∥FC,∴四边形AFCH为平行四边形,∴AF∥CH,
又∵EH∥FG,∴四边形MFNH为平行四边形.
(2)由(1)可知四边形AFCH为平行四边形,∴∠NCF=∠MAH,
∵EH∥FG,∴∠AMH=∠AFN,
∵AF∥CH,∴∠AFN=∠CNF,∴∠AMH=∠CNF.
在△AMH和△CNF中,∴△AMH≌△CNF(AAS).
23.解析 (1)证明:∵DE∥AC,DF∥AB,,∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠B,
又∵AB=AC,∴∠B=∠C,∴∠FDC=∠C,∴DF=FC,
∴DE+DF=AF+FC=AC.
(2)当点D在边BC的延长线上时,DE-DF=AC.
当点D在边BC的反向延长线上时,DF-DE=AC.
(3)当点D在边BC上时,DF=AC-DE=10-7=3.
当点D在边BC的反向延长线上时,DF=AC+DE=10+7=17.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《第五章 平行四边形》单元测试题
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.下列说法属于平行四边形判定方法的有( )
①两组对边分别平行的四边形是平行四边形;
②平行四边形的对角线互相平分;
③两组对边分别相等的四边形是平行四边形;
④平行四边形的每组对边平行且相等;
⑤两条对角线互相平分的四边形是平行四边形
A.5个 B.4个 C.3个 D.2个
2.若n边形的内角和是它外角和的3倍,则n等于( )
A.6 B.7 C.8 D.9
3.在平行四边形ABCD中,若∠A+∠C=120°,则∠C的度数是( )
A.120° B.30° C.60° D.90°
4.如图所示,在平行四边形ABCD中,AC和BD相交于点O,AB⊥AC,∠ABD=30°,AC=2cm,则平行四边形ABCD的周长是( )
A.2()cm B.4cm C.2(-)cm D.2(2+)cm
5.如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=50°,∠BAC=80°,则∠1的度数为( )
A.60° B.50° C.40° D.25°
第5题图 第6题图
6.如图所示,M是平行四边形ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S1,△ABM的面积为S2,则下列关于S,S1,S2的关系中,正确的是( )
A.S>S1+S2 B.S=S1+S2 C.S<S1+S2 D.S,S1,S2的关系无法确定
7.如图所示,在△ABC中,D、E、F分别是BC、AC、AD的中点,若△ABC的面积是40,则四边形BDEF的面积是( )
A.10 B.12.5 C.15 D.20
8.如图所示,在△ABC中,D,E分别是AB,BC的中点.点F在DE的延长线上,若添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠BCF B.∠B=∠F C.AC=CF D.AD=CF
9.如图所示,在五边形 ABCDE中,若去掉一个30°的角后得到 BCDEMN一个六边形,则∠1+∠2的度数为( )
A.210° B.110° C.150° D.100°
10.如图所示,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②四边形BGFE是平行四边形;③△FEG≌△BGE;④EG=EF,其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
11.如图所示,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添
加一个条件______________,使四边形ABCD是平行四边形.(填一个即可)
12.如图所示,在平行四边形ABCD中,已知AD=36,AB=24,∠BAD的平分线AE交BC边于点E,则CE的长为_________.
13.如图所示,已知P是平行四边形ABCD的边BC上一点,连接AP,DP,如果AB=AD=AP,∠B=80°,那么∠CDP的度数为___________.
14.小明计算一个多边形的内角和时误把一个外角加进去了,得其和为2260°,则这个多边形的边数为__________.
15.如图所示,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则平行四边形ABCD的周长为___________.
16.如图所示,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF若∠A=30°,BC=2,CF=3,则CD=___________.
17.如图所示,在平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,若S△BEF=4,则S平行四边形ABCD=___________.
18.如图所示,点A、B、C的坐标分别是(0,2)、(2,2)、(0,-1),那么以点A、B、C为顶点的平行四边形的第四个顶点D的坐标是___________.
三、解答题(共46分)
19.(8分)已知一个多边形的所有内角的和与它的外角之和为1620°,求这个多边形的边数.
20.(8分)如图所示,AD、BF相交于点O,点E、C在BF上,BE=FC,AC=DE,AB=DF,求证:四边形ABDF是平行四边形.
21.(10分)如图所示,在平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AE的长.
22.(10分)如图所示,在平行四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
求证:(1)四边形MFNH为平行四边形;
(2)△AMh≌△CNF.
23.(10分)在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC;
(2)当点D在边BC的延长线上时,如图②.当点D在边BC的反向延长线上时,如图③.
请分别写出图②③中DE、DF、AC之间的等量关系式(不需要证明);
(3)若AC=10,DE=7,问DF的长为多少?
参考答案
一、选择题
1.C 2.C 3.C 4.A 5.B 6.B 7.C 8.A 9.A 10.D
二、填空题
11.AB∥CD(答案不唯一) 12. 12 13. 30° 14. 14 15. 16 cm
16. 17. 18 18. (-2,-1)或(2,-1)或(2,5)
三、解答题
19.解析 设这个多边形的边数是n.
由题意得(n-2)·180°+360°=1620°,解得n=9.
答:这个多边形的边数n是9.
20.证明 ∵BE=CF,∴BE+CE=CF+CE,即BC=FE.
在△ABC和△DFE中,∴△ABC≌△DFE(SSS),
∴∠ABF=∠DFE,∴AB∥DF,
又∵AB=DF,∴四边形ABDF是平行四边形.
21.解析 (1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∴∠OBE=∠ODF.
在△OBE与△ODF中,∠OBE=∠ODF,∠BOE=∠DOF,BE=DF,
∴△OBE≌△ODF(AAS),∴BO=DO.
(2)∵EF⊥AB,AB∥DC,∴∠GEA=∠GFD=90°.
∵∠A=45°,∴∠G=∠A=45°,∴AE=GE.
∵BD⊥AD,∴∠ADB=∠GDO=90°,∴∠GOD=∠G=45°,
∴DG=DO,易知EF⊥CD,∴OF=FG=1.
由(1)可知△OBE≌△ODF,∴OE=OF=1,
∴GE=OE+OF+FG=3,∴AE=3.
22.证明 (1)连接BD(图略),
∵E、H分别为AB、AD的中点,∴EH为△ABD的中位线,∴EH∥BD.
同理FG∥BD.∴EH∥FG.
在平行四边形ABCD中,AD∥BC,AD=BC,
∵H为AD的中点,∴AH=AD,∵F为BC的中点,∴FC=BC,∴AH=FC,
又∵AH∥FC,∴四边形AFCH为平行四边形,∴AF∥CH,
又∵EH∥FG,∴四边形MFNH为平行四边形.
(2)由(1)可知四边形AFCH为平行四边形,∴∠NCF=∠MAH,
∵EH∥FG,∴∠AMH=∠AFN,
∵AF∥CH,∴∠AFN=∠CNF,∴∠AMH=∠CNF.
在△AMH和△CNF中,∴△AMH≌△CNF(AAS).
23.解析 (1)证明:∵DE∥AC,DF∥AB,,∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠B,
又∵AB=AC,∴∠B=∠C,∴∠FDC=∠C,∴DF=FC,
∴DE+DF=AF+FC=AC.
(2)当点D在边BC的延长线上时,DE-DF=AC.
当点D在边BC的反向延长线上时,DF-DE=AC.
(3)当点D在边BC上时,DF=AC-DE=10-7=3.
当点D在边BC的反向延长线上时,DF=AC+DE=10+7=17.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
