2021-2022学年安徽省亳州市蒙城六中九年级(上)期中数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年安徽省亳州市蒙城六中九年级(上)期中数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 22:16:03 | ||
图片预览


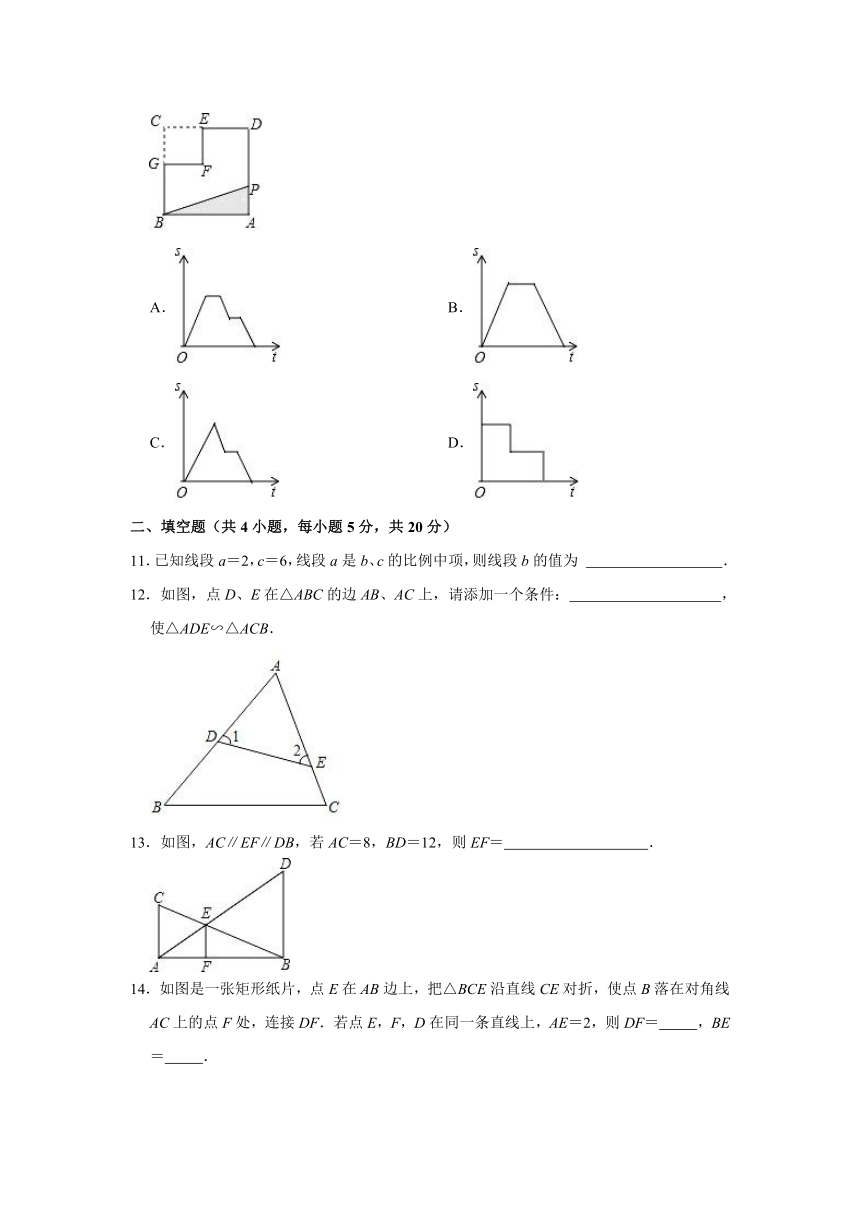


文档简介
2021-2022学年安徽省亳州市蒙城六中九年级第一学期期中数学试卷
一、选择题(共10小题,每小题4分,共40分)
1.若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为( )
A.0,5 B.0,1 C.﹣4,5 D.﹣4,1
2.如图,在△ABC中,EF∥BC,,则=( )
A. B. C. D.
3.已知点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,则下列关系式一定正确的是( )
A.x1<x2<0 B.x1<0<x2 C.x2<x1<0 D.x2<0<x1
4.若,则等于( )
A.8 B.9 C.10 D.11
5.已知:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.3:2 C.4:9 D.9:4
6.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连接AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
A.点O为位似中心且位似比为2:1
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
7.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )
A.x1=﹣7,x2=3 B.x1=﹣6,x2=4 C.x1=6,x2=﹣4 D.x1=7,x2=﹣3
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3 B. C. D.2
9.如图,梯形ABCD中,AB∥CD,对角线AC、BD相交于O,下面四个结论:
①△AOB∽△COD
②△AOD∽△BOC
③S△DOC:S△BOA=DC:AB
④S△AOD=S△BOC.其中结论始终正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B.
C. D.
二、填空题(共4小题,每小题5分,共20分)
11.已知线段a=2,c=6,线段a是b、c的比例中项,则线段b的值为 .
12.如图,点D、E在△ABC的边AB、AC上,请添加一个条件: ,使△ADE∽△ACB.
13.如图,AC∥EF∥DB,若AC=8,BD=12,则EF= .
14.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= ,BE= .
三、解答题(共2小题,每小题8分,共16分)
15.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
16.如图,在边长为1个单位长度的小正方形网格中.
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
四、解答题(共2小题,每小题8分,共16分)
17.如图,在平面直角坐标系中,一次函数y=﹣x+5的图象与反比例函数y=(k≠0)的图象相交于点A(8,t)和点B.
(1)求反比例函数的关系式和点B的坐标;
(2)结合图象,请直接写出在第一象限内,当﹣x+5>时x的取值范围.
18.阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依此类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.则:
(1)等比数列2,4,8,…的公比q为 ,第4项是 .
(2)如果一个数列a1,a2,a3,a4…是等比数列,且公比为q,那么根据定义可得到:
所以:a2=a1q,a3=a2q=a1q2,a4=a3q=a1q3.
由此可得:an= (用a1和q的代数式表示).
(3)若一等比数列的公比q=5,第2项是10,请求它的第1项与第5项.
五、解答题(共2小题,每小题10分,共20分)
19.某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升(0≤x≤a)时,满足y=2x,下降时,y与x成反比.
(1)求a的值,并求当a≤x≤8时,y与x的函数表达式;
(2)若血液中药物浓度不低于3微克/毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
20.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
六、(本大题12分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:△ADE∽△ACB;
(2)求证:DE=CE.
七、(本大题12分)
22.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
八、(本大题14分)
23.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE.
(1)求证:DH=CE;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当=时,值为 .(直接写答案)
参考答案
一、选择题(共10小题,每小题4分,共40分)
1.若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为( )
A.0,5 B.0,1 C.﹣4,5 D.﹣4,1
【分析】可将y=(x﹣2)2+k的右边运用完全平方公式展开,再与y=x2+bx+5比较,即可得出b、k的值.
解:∵y=(x﹣2)2+k=x2﹣4x+4+k=x2﹣4x+(4+k),
又∵y=x2+bx+5,
∴x2﹣4x+(4+k)=x2+bx+5,
∴b=﹣4,k=1.
故选:D.
2.如图,在△ABC中,EF∥BC,,则=( )
A. B. C. D.
【分析】平行于三角形一边的直线截其他两边,所得的对应线段成比例,列出比例式即可得到所求的比值.
解:∵EF∥BC,
∴,
又∵,
∴=,
故选:C.
3.已知点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,则下列关系式一定正确的是( )
A.x1<x2<0 B.x1<0<x2 C.x2<x1<0 D.x2<0<x1
【分析】利用反比例函数图象上点的坐标特征求出x1与x2,然后对各选项进行判断.
解:∵点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,
∴4=﹣,8=﹣,
∴x1=﹣,x2=﹣,
∴x1<x2<0.
故选:A.
4.若,则等于( )
A.8 B.9 C.10 D.11
【分析】设=k,得出a=2k,b=3k,c=4k,代入求出即可.
解:设=k,
则a=2k,b=3k,c=4k,
即
=
=
=10,
故选:C.
5.已知:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.3:2 C.4:9 D.9:4
【分析】由AB∥CD,AD与BC交于点O,AD:OD=5:3,可得△AOB∽△DOC,AO:OD=2:3,又三角形的面积比等于相似比的平方可得结论.
解:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,
∴△AOB∽△DOC,且AO:OD=2:3,
∴S△AOB:S△DOC=AO2:OD2=4:9.
故选:C.
6.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连接AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
A.点O为位似中心且位似比为2:1
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
【分析】根据位似图形的性质,得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出 ②△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
解:∵如图,任取一点O,连接AO,BO,CO,并取它们的中点D、E、F,得△DEF,
∴将△ABC的三边缩小到原来的,此时点O为位似中心且△DEF与△ABC的位似比为1:2,故选项A说法错误,符合题意;
△ABC与△DEF是位似图形,故选项B说法正确,不合题意;
△ABC与△DEF是相似图形,故选项C说法正确,不合题意;
△ABC与△DEF的面积之比为4:1,故选项D说法正确,不合题意;
故选:A.
7.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )
A.x1=﹣7,x2=3 B.x1=﹣6,x2=4 C.x1=6,x2=﹣4 D.x1=7,x2=﹣3
【分析】函数的对称轴为x=﹣=﹣=2,即可求解.
解:函数的对称轴为x=﹣=﹣=2,
而两个交点之间的距离为10,
则两个交点的坐标分别为:(7,0)、(﹣3,0),
故选:D.
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3 B. C. D.2
【分析】先作出函数图象,在抛物线上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,求出PQ的最小值就是这两个函数的“和谐值”.
解:如图,在抛物线y=x2﹣2x+3上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,
设P(t,t2﹣2t+3),则Q(t,t﹣2),
∴PQ=t2﹣2t+3﹣(t﹣2)
=t2﹣3t+5
=(t﹣)2+,
∴当t=时,PQ有最小值,最小值为,
∴抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为,
故选:B.
9.如图,梯形ABCD中,AB∥CD,对角线AC、BD相交于O,下面四个结论:
①△AOB∽△COD
②△AOD∽△BOC
③S△DOC:S△BOA=DC:AB
④S△AOD=S△BOC.其中结论始终正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据已知及相似三角形的判定方法对各个选项进行验证,从而得到最后答案.
解:∵AB∥CD
∴△AOB∽△COD(①正确)
∴S△DOC:S△BOA=(③不正确)
∵△ABD与△ABC等高同底
∴S△ABD=S△ABC∵S△ABD﹣S△AOB=S△ABC﹣S△AOB∴S△AOD=S△BOC(④正确)
∴共有2个正确的
故选:B.
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B.
C. D.
【分析】分析动点P在每段路径上的运动的过程中的面积增大、减小或不变的趋势即可.
解:由点P的运动可知,当点P在GF、ED边上时△ABP的面积不变,则对应图象为平行于t轴的线段,则B、C错误.点P在AD、EF、GB上运动时,△ABP的面积分别处于增、减变化过程.故D排除
故选:A.
二、填空题(共4小题,每小题5分,共20分)
11.已知线段a=2,c=6,线段a是b、c的比例中项,则线段b的值为 .
【分析】根据线段比例中项的概念,可得b:a=a:c,可得a2=bc,故b的值可求.
解:若线段a是b、c的比例中项,
即a2=bc,
∵a=2,c=6,
∴b==,
故答案为:.
12.如图,点D、E在△ABC的边AB、AC上,请添加一个条件: ∠1=∠C或∠2=∠B或= ,使△ADE∽△ACB.
【分析】由于△ADE和△ACB有一个公共角,所以根据有两组角对应相等的两个三角形相似,可添加∠1=∠C或∠2=∠B或=,使△ADE∽△ACB.
解:∵∠DAE=∠CAB
∴当∠1=∠C或∠2=∠B或=时,△ADE∽△ACB.
故答案是:∠1=∠C或∠2=∠B或=,
13.如图,AC∥EF∥DB,若AC=8,BD=12,则EF= .
【分析】根据平行线AC∥EF分线段成比例得到=.同理,=,则由比例的性质得到=,根据等量代换推知=,所以把相关数据代入即可求得EF的值.
解:如图,∵AC∥EF,
∴=.
又∵EF∥DB,
∴=,
则由比例的性质知=,即=,
∴=,
∵AC=8,BD=12,
∴=
∴EF=.
故答案是:.
14.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= 2 ,BE= ﹣1 .
【分析】根据矩形的性质得到AD=BC,∠ADC=∠B=∠DAE=90°,根据折叠的性质得到CF=BC,∠CFE=∠B=90°,EF=BE,根据全等三角形的性质得到DF=AE=2;根据相似三角形的性质即可得到结论.
解:∵四边形ABCD是矩形,
∴AD=BC,∠ADC=∠B=∠DAE=90°,
∵把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,
∴CF=BC,∠CFE=∠B=90°,EF=BE,
∴CF=AD,∠CFD=90°,
∴∠ADE+∠CDF=∠CDF+∠DCF=90°,
∴∠ADF=∠DCF,
∴△ADE≌△FCD(ASA),
∴DF=AE=2;
∵∠AFE=∠CFD=90°,
∴∠AFE=∠DAE=90°,
∵∠AEF=∠DEA,
∴△AEF∽△DEA,
∴,
∴=,
∴EF=﹣1(负值舍去),
∴BE=EF=﹣1,
方法二:∵AB∥CD,
∴S△ACD=S△DCE,
∴S△ACD﹣S△DCF=S△DCE﹣S△DCF,
∴S△ADF=S△ECF,
由题意知,BC=CF,S△ACD=S△ABC,S△ECF=S△BCE,
∴S△ACD﹣S△ADF=S△ABC﹣S△CEF=S△ABC﹣S△BCE,
∴S△DCF=S△ACE,
∴×DF CF=AE BC,
∵CF=BC,
∴DF=AE=2,
设BE=x,
∵AE∥CD,
∴△AEF∽△CDF,
∴=,
∴=,
解得:x=﹣1(负值舍去 ),
∴BE=﹣1.
故答案为:2,﹣1.
三、解答题(共2小题,每小题8分,共16分)
15.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
【分析】(1)由矩形性质得AD∥BC,进而由平行线的性质得∠AEB=∠DAF,再根据两角对应相等的两个三角形相似;
(2)由E是BC的中点,求得BE,再由勾股定理求得AE,再由相似三角形的比例线段求得DF.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA;
(2)∵E是BC的中点,BC=4,
∴BE=2,
∵AB=6,
∴AE=,
∵四边形ABCD是矩形,
∴AD=BC=4,
∵△ABE∽△DFA,
∴,
∴.
16.如图,在边长为1个单位长度的小正方形网格中.
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
【分析】(1)将△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1,如图所示;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,如图所示.
解:(1)根据题意画出图形,△A1B1C1为所求三角形;
(2)根据题意画出图形,△A2B2C2为所求三角形.
四、解答题(共2小题,每小题8分,共16分)
17.如图,在平面直角坐标系中,一次函数y=﹣x+5的图象与反比例函数y=(k≠0)的图象相交于点A(8,t)和点B.
(1)求反比例函数的关系式和点B的坐标;
(2)结合图象,请直接写出在第一象限内,当﹣x+5>时x的取值范围.
【分析】(1)把点A(8,t)代入y=﹣x+5,求得t的值,然后根据待定系数法即可求得反比例函数的关系式,解析式联立成方程组,解方程组求得点B的坐标;
(2)根据图象即可求得.
解:(1)∵A(8,t)在一次函数y=﹣x+5的图象上,
∴t=﹣×8+5=1,
∴A(8,1),
∵反比例函数y=(k≠0)的图象经过点A(8,1),
∴k=8×1=8,
∴反比例函数的解析式为y=,
解得或,
∴B的坐标为(2,4);
(2)由图象可知,在第一象限内,当﹣x+5>时x的取值范围是2<x<8.
18.阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依此类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.则:
(1)等比数列2,4,8,…的公比q为 2 ,第4项是 16 .
(2)如果一个数列a1,a2,a3,a4…是等比数列,且公比为q,那么根据定义可得到:
所以:a2=a1q,a3=a2q=a1q2,a4=a3q=a1q3.
由此可得:an= an=a1 qn﹣1 (用a1和q的代数式表示).
(3)若一等比数列的公比q=5,第2项是10,请求它的第1项与第5项.
【分析】(1)由第二项除以第一项求出公比q的值,确定出第4项即可;
(2)根据题中的定义归纳总结得到通项公式即可;
(3)由公比q与第二项的值求出第一项的值,进而确定出第5项的值.
解:(1),第4项是16;
(2)归纳总结得:an=a1 qn﹣1;
(3)∵等比数列的公比q=5,第二项为10,
∴a1==2,a5=a1 q4=2×54=1250.
故答案为:(1)2;16;(2)an=a1 qn﹣1.
五、解答题(共2小题,每小题10分,共20分)
19.某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升(0≤x≤a)时,满足y=2x,下降时,y与x成反比.
(1)求a的值,并求当a≤x≤8时,y与x的函数表达式;
(2)若血液中药物浓度不低于3微克/毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
【分析】(1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)把y=3分别代入正比例函数和反比例函数解析式求出自变量的值,进而得出答案.
解:(1)有图象知,a=3;
又由题意可知:当3≤x≤8时,y与x成反比,设.
由图象可知,当x=3时,y=6,
∴m=3×6=18;
∴y=(3≤x≤8);
(2)把y=3分别代入y=2x和y=得,x=1.5和x=6,
∵6﹣1.5=4.5>4,
∴抗菌新药可以作为有效药物投入生产.
20.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
【分析】(1)根据CE=CF,列出方程即可解决问题;
(2)分两种情形分别讨论即可①当=时,△ECF∽△ADC,②当=时,△FCE∽△ADC;
解:(1)当CE=CF时,△CEF是等腰三角形,
∴4t=12﹣2t,
∴t=2.
(2)①当=时,△ECF∽△ADC,
∴=,
∴t=3.
②当=时,△FCE∽△ADC,
∴=,
∴t=,
综上所述,当t=s或3s时,以点E,C,F为顶点的三角形与△ACD相似.
六、(本大题12分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:△ADE∽△ACB;
(2)求证:DE=CE.
【分析】(1)由题可知∠ABE∽△ACD,所以,即,又∠A=∠A,所以△ADE∽△ACB;
(2)由(1)知∠AED=∠ABC,结合三角形外角的性质定理及平分线的性质可得∠CDE=∠ABE+∠ACD,可得结论.
【解答】证明:(1)如图,∵∠A=∠A,∠ABE=∠ACD,
∴△ABE∽△ACD,
∴,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB;
(2)由(1)知,△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠CBE+∠ABE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE+∠ACD,
∴DE=CE.
七、(本大题12分)
22.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
【分析】(1)只需任选一个点作为顶点,同号两数作为二次项的系数,用顶点式表示两个为“同簇二次函数”的函数表达式即可.
(2)由y1的图象经过点A(1,1)可以求出m的值,然后根据y1+y2与y1为“同簇二次函数”就可以求出函数y2的表达式,然后将函数y2的表达式转化为顶点式,在利用二次函数的性质就可以解决问题.
解:(1)设顶点为(h,k)的二次函数的关系式为y=a(x﹣h)2+k,
当a=2,h=3,k=4时,
二次函数的关系式为y=2(x﹣3)2+4.
∵2>0,
∴该二次函数图象的开口向上.
当a=3,h=3,k=4时,
二次函数的关系式为y=3(x﹣3)2+4.
∵3>0,
∴该二次函数图象的开口向上.
∵两个函数y=2(x﹣3)2+4与y=3(x﹣3)2+4顶点相同,开口都向上,
∴两个函数y=2(x﹣3)2+4与y=3(x﹣3)2+4是“同簇二次函数”.
∴符合要求的两个“同簇二次函数”可以为:y=2(x﹣3)2+4与y=3(x﹣3)2+4(答案不唯一).
(2)∵y1的图象经过点A(1,1),
∴2×12﹣4×m×1+2m2+1=1.
整理得:m2﹣2m+1=0.
解得:m1=m2=1.
∴y1=2x2﹣4x+3
=2(x﹣1)2+1.
∴y1+y2=2x2﹣4x+3+ax2+bx+5
=(a+2)x2+(b﹣4)x+8
∵y1+y2与y1为“同簇二次函数”,
∴y1+y2=(a+2)(x﹣1)2+1
=(a+2)x2﹣2(a+2)x+(a+2)+1.
其中a+2>0,即a>﹣2.
∴.
解得:.
∴函数y2的表达式为:y2=5x2﹣10x+5.
∴y2=5x2﹣10x+5
=5(x﹣1)2.
∴函数y2的图象的对称轴为x=1.
∵5>0,
∴函数y2的图象开口向上.
①当0≤x≤1时,∵函数y2的图象开口向上,
∴y2随x的增大而减小,
∴当x=0时,y2取最大值,最大值为5×(0﹣1)2=5,
②当1≤x≤3时,∵函数y2的图象开口向上,
∴y2随x的增大而增大,
∴当x=3时,y2取最大值,
最大值为5(3﹣1)2=20.
综上所述:当0≤x≤3时,y2的最大值为20.
八、(本大题14分)
23.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE.
(1)求证:DH=CE;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当=时,值为 .(直接写答案)
【分析】(1)可得∠CHD=∠BEC,根据AAS可证明△DHC≌△CEB,即可求解;
(2))由△DHC≌△CEB,及DH∥BC,可得==,则GC=2GH,可求出GH的长;
(3)设S△DGH=16a,则S△BCG=49a,S△DCG=28a,求出S1和S2即可得出答案.
【解答】(1)证明:∵四边形ABCD是正方形,
∴CD=BC,∠HDC=∠BCE=90°,
∴∠DHC+∠DCH=90°,
∵CH⊥BE,
∴∠EFC=90°,
∴∠ECF+∠BEC=90°,
∴∠CHD=∠BEC,
在△DHC和△CEB中,
,
∴△DHC≌△CEB(AAS),
∴DH=CE;
(2)解:∵△DHC≌△CEB,
∴CH=BE,DH=CE,
∵点E是CD的中点,
∴CE=DE=CD,
∵CD=CB,
∴DH=BC,
∵DH∥BC,
∴==,
∴CG=2GH,
设GH=x,则CG=2x,
∴3x=8,
∴x=
即GH=;
(3)解:当的值为时,则=,
∵DH=CE,DC=BC,
∴=,
∵DH∥BC,
∴==,
∴=,=,
设S△DGH=16a,则S△BCG=49a,S△DCG=28a,
∴S△BCD=49a+28a=77a,
∴S1=2S△BCD=154a,
∵S△DEG:S△CEG=3:4,
∴S△DEG=12a,
∴S2=16a+12a=28a,
∴==,
故答案为:.
一、选择题(共10小题,每小题4分,共40分)
1.若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为( )
A.0,5 B.0,1 C.﹣4,5 D.﹣4,1
2.如图,在△ABC中,EF∥BC,,则=( )
A. B. C. D.
3.已知点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,则下列关系式一定正确的是( )
A.x1<x2<0 B.x1<0<x2 C.x2<x1<0 D.x2<0<x1
4.若,则等于( )
A.8 B.9 C.10 D.11
5.已知:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.3:2 C.4:9 D.9:4
6.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连接AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
A.点O为位似中心且位似比为2:1
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
7.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )
A.x1=﹣7,x2=3 B.x1=﹣6,x2=4 C.x1=6,x2=﹣4 D.x1=7,x2=﹣3
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3 B. C. D.2
9.如图,梯形ABCD中,AB∥CD,对角线AC、BD相交于O,下面四个结论:
①△AOB∽△COD
②△AOD∽△BOC
③S△DOC:S△BOA=DC:AB
④S△AOD=S△BOC.其中结论始终正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B.
C. D.
二、填空题(共4小题,每小题5分,共20分)
11.已知线段a=2,c=6,线段a是b、c的比例中项,则线段b的值为 .
12.如图,点D、E在△ABC的边AB、AC上,请添加一个条件: ,使△ADE∽△ACB.
13.如图,AC∥EF∥DB,若AC=8,BD=12,则EF= .
14.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= ,BE= .
三、解答题(共2小题,每小题8分,共16分)
15.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
16.如图,在边长为1个单位长度的小正方形网格中.
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
四、解答题(共2小题,每小题8分,共16分)
17.如图,在平面直角坐标系中,一次函数y=﹣x+5的图象与反比例函数y=(k≠0)的图象相交于点A(8,t)和点B.
(1)求反比例函数的关系式和点B的坐标;
(2)结合图象,请直接写出在第一象限内,当﹣x+5>时x的取值范围.
18.阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依此类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.则:
(1)等比数列2,4,8,…的公比q为 ,第4项是 .
(2)如果一个数列a1,a2,a3,a4…是等比数列,且公比为q,那么根据定义可得到:
所以:a2=a1q,a3=a2q=a1q2,a4=a3q=a1q3.
由此可得:an= (用a1和q的代数式表示).
(3)若一等比数列的公比q=5,第2项是10,请求它的第1项与第5项.
五、解答题(共2小题,每小题10分,共20分)
19.某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升(0≤x≤a)时,满足y=2x,下降时,y与x成反比.
(1)求a的值,并求当a≤x≤8时,y与x的函数表达式;
(2)若血液中药物浓度不低于3微克/毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
20.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
六、(本大题12分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:△ADE∽△ACB;
(2)求证:DE=CE.
七、(本大题12分)
22.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
八、(本大题14分)
23.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE.
(1)求证:DH=CE;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当=时,值为 .(直接写答案)
参考答案
一、选择题(共10小题,每小题4分,共40分)
1.若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为( )
A.0,5 B.0,1 C.﹣4,5 D.﹣4,1
【分析】可将y=(x﹣2)2+k的右边运用完全平方公式展开,再与y=x2+bx+5比较,即可得出b、k的值.
解:∵y=(x﹣2)2+k=x2﹣4x+4+k=x2﹣4x+(4+k),
又∵y=x2+bx+5,
∴x2﹣4x+(4+k)=x2+bx+5,
∴b=﹣4,k=1.
故选:D.
2.如图,在△ABC中,EF∥BC,,则=( )
A. B. C. D.
【分析】平行于三角形一边的直线截其他两边,所得的对应线段成比例,列出比例式即可得到所求的比值.
解:∵EF∥BC,
∴,
又∵,
∴=,
故选:C.
3.已知点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,则下列关系式一定正确的是( )
A.x1<x2<0 B.x1<0<x2 C.x2<x1<0 D.x2<0<x1
【分析】利用反比例函数图象上点的坐标特征求出x1与x2,然后对各选项进行判断.
解:∵点A(x1,4),B(x2,8)都在反比例函数y=﹣的图象上,
∴4=﹣,8=﹣,
∴x1=﹣,x2=﹣,
∴x1<x2<0.
故选:A.
4.若,则等于( )
A.8 B.9 C.10 D.11
【分析】设=k,得出a=2k,b=3k,c=4k,代入求出即可.
解:设=k,
则a=2k,b=3k,c=4k,
即
=
=
=10,
故选:C.
5.已知:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.3:2 C.4:9 D.9:4
【分析】由AB∥CD,AD与BC交于点O,AD:OD=5:3,可得△AOB∽△DOC,AO:OD=2:3,又三角形的面积比等于相似比的平方可得结论.
解:如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,
∴△AOB∽△DOC,且AO:OD=2:3,
∴S△AOB:S△DOC=AO2:OD2=4:9.
故选:C.
6.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连接AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
A.点O为位似中心且位似比为2:1
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
【分析】根据位似图形的性质,得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出 ②△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
解:∵如图,任取一点O,连接AO,BO,CO,并取它们的中点D、E、F,得△DEF,
∴将△ABC的三边缩小到原来的,此时点O为位似中心且△DEF与△ABC的位似比为1:2,故选项A说法错误,符合题意;
△ABC与△DEF是位似图形,故选项B说法正确,不合题意;
△ABC与△DEF是相似图形,故选项C说法正确,不合题意;
△ABC与△DEF的面积之比为4:1,故选项D说法正确,不合题意;
故选:A.
7.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )
A.x1=﹣7,x2=3 B.x1=﹣6,x2=4 C.x1=6,x2=﹣4 D.x1=7,x2=﹣3
【分析】函数的对称轴为x=﹣=﹣=2,即可求解.
解:函数的对称轴为x=﹣=﹣=2,
而两个交点之间的距离为10,
则两个交点的坐标分别为:(7,0)、(﹣3,0),
故选:D.
8.我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为( )
A.3 B. C. D.2
【分析】先作出函数图象,在抛物线上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,求出PQ的最小值就是这两个函数的“和谐值”.
解:如图,在抛物线y=x2﹣2x+3上取一点P,作PQ∥y轴交直线y=x﹣2于点Q,
设P(t,t2﹣2t+3),则Q(t,t﹣2),
∴PQ=t2﹣2t+3﹣(t﹣2)
=t2﹣3t+5
=(t﹣)2+,
∴当t=时,PQ有最小值,最小值为,
∴抛物线y=x2﹣2x+3与直线y=x﹣2的“和谐值”为,
故选:B.
9.如图,梯形ABCD中,AB∥CD,对角线AC、BD相交于O,下面四个结论:
①△AOB∽△COD
②△AOD∽△BOC
③S△DOC:S△BOA=DC:AB
④S△AOD=S△BOC.其中结论始终正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据已知及相似三角形的判定方法对各个选项进行验证,从而得到最后答案.
解:∵AB∥CD
∴△AOB∽△COD(①正确)
∴S△DOC:S△BOA=(③不正确)
∵△ABD与△ABC等高同底
∴S△ABD=S△ABC∵S△ABD﹣S△AOB=S△ABC﹣S△AOB∴S△AOD=S△BOC(④正确)
∴共有2个正确的
故选:B.
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B.
C. D.
【分析】分析动点P在每段路径上的运动的过程中的面积增大、减小或不变的趋势即可.
解:由点P的运动可知,当点P在GF、ED边上时△ABP的面积不变,则对应图象为平行于t轴的线段,则B、C错误.点P在AD、EF、GB上运动时,△ABP的面积分别处于增、减变化过程.故D排除
故选:A.
二、填空题(共4小题,每小题5分,共20分)
11.已知线段a=2,c=6,线段a是b、c的比例中项,则线段b的值为 .
【分析】根据线段比例中项的概念,可得b:a=a:c,可得a2=bc,故b的值可求.
解:若线段a是b、c的比例中项,
即a2=bc,
∵a=2,c=6,
∴b==,
故答案为:.
12.如图,点D、E在△ABC的边AB、AC上,请添加一个条件: ∠1=∠C或∠2=∠B或= ,使△ADE∽△ACB.
【分析】由于△ADE和△ACB有一个公共角,所以根据有两组角对应相等的两个三角形相似,可添加∠1=∠C或∠2=∠B或=,使△ADE∽△ACB.
解:∵∠DAE=∠CAB
∴当∠1=∠C或∠2=∠B或=时,△ADE∽△ACB.
故答案是:∠1=∠C或∠2=∠B或=,
13.如图,AC∥EF∥DB,若AC=8,BD=12,则EF= .
【分析】根据平行线AC∥EF分线段成比例得到=.同理,=,则由比例的性质得到=,根据等量代换推知=,所以把相关数据代入即可求得EF的值.
解:如图,∵AC∥EF,
∴=.
又∵EF∥DB,
∴=,
则由比例的性质知=,即=,
∴=,
∵AC=8,BD=12,
∴=
∴EF=.
故答案是:.
14.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= 2 ,BE= ﹣1 .
【分析】根据矩形的性质得到AD=BC,∠ADC=∠B=∠DAE=90°,根据折叠的性质得到CF=BC,∠CFE=∠B=90°,EF=BE,根据全等三角形的性质得到DF=AE=2;根据相似三角形的性质即可得到结论.
解:∵四边形ABCD是矩形,
∴AD=BC,∠ADC=∠B=∠DAE=90°,
∵把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,
∴CF=BC,∠CFE=∠B=90°,EF=BE,
∴CF=AD,∠CFD=90°,
∴∠ADE+∠CDF=∠CDF+∠DCF=90°,
∴∠ADF=∠DCF,
∴△ADE≌△FCD(ASA),
∴DF=AE=2;
∵∠AFE=∠CFD=90°,
∴∠AFE=∠DAE=90°,
∵∠AEF=∠DEA,
∴△AEF∽△DEA,
∴,
∴=,
∴EF=﹣1(负值舍去),
∴BE=EF=﹣1,
方法二:∵AB∥CD,
∴S△ACD=S△DCE,
∴S△ACD﹣S△DCF=S△DCE﹣S△DCF,
∴S△ADF=S△ECF,
由题意知,BC=CF,S△ACD=S△ABC,S△ECF=S△BCE,
∴S△ACD﹣S△ADF=S△ABC﹣S△CEF=S△ABC﹣S△BCE,
∴S△DCF=S△ACE,
∴×DF CF=AE BC,
∵CF=BC,
∴DF=AE=2,
设BE=x,
∵AE∥CD,
∴△AEF∽△CDF,
∴=,
∴=,
解得:x=﹣1(负值舍去 ),
∴BE=﹣1.
故答案为:2,﹣1.
三、解答题(共2小题,每小题8分,共16分)
15.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
【分析】(1)由矩形性质得AD∥BC,进而由平行线的性质得∠AEB=∠DAF,再根据两角对应相等的两个三角形相似;
(2)由E是BC的中点,求得BE,再由勾股定理求得AE,再由相似三角形的比例线段求得DF.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA;
(2)∵E是BC的中点,BC=4,
∴BE=2,
∵AB=6,
∴AE=,
∵四边形ABCD是矩形,
∴AD=BC=4,
∵△ABE∽△DFA,
∴,
∴.
16.如图,在边长为1个单位长度的小正方形网格中.
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
【分析】(1)将△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1,如图所示;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,如图所示.
解:(1)根据题意画出图形,△A1B1C1为所求三角形;
(2)根据题意画出图形,△A2B2C2为所求三角形.
四、解答题(共2小题,每小题8分,共16分)
17.如图,在平面直角坐标系中,一次函数y=﹣x+5的图象与反比例函数y=(k≠0)的图象相交于点A(8,t)和点B.
(1)求反比例函数的关系式和点B的坐标;
(2)结合图象,请直接写出在第一象限内,当﹣x+5>时x的取值范围.
【分析】(1)把点A(8,t)代入y=﹣x+5,求得t的值,然后根据待定系数法即可求得反比例函数的关系式,解析式联立成方程组,解方程组求得点B的坐标;
(2)根据图象即可求得.
解:(1)∵A(8,t)在一次函数y=﹣x+5的图象上,
∴t=﹣×8+5=1,
∴A(8,1),
∵反比例函数y=(k≠0)的图象经过点A(8,1),
∴k=8×1=8,
∴反比例函数的解析式为y=,
解得或,
∴B的坐标为(2,4);
(2)由图象可知,在第一象限内,当﹣x+5>时x的取值范围是2<x<8.
18.阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依此类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.则:
(1)等比数列2,4,8,…的公比q为 2 ,第4项是 16 .
(2)如果一个数列a1,a2,a3,a4…是等比数列,且公比为q,那么根据定义可得到:
所以:a2=a1q,a3=a2q=a1q2,a4=a3q=a1q3.
由此可得:an= an=a1 qn﹣1 (用a1和q的代数式表示).
(3)若一等比数列的公比q=5,第2项是10,请求它的第1项与第5项.
【分析】(1)由第二项除以第一项求出公比q的值,确定出第4项即可;
(2)根据题中的定义归纳总结得到通项公式即可;
(3)由公比q与第二项的值求出第一项的值,进而确定出第5项的值.
解:(1),第4项是16;
(2)归纳总结得:an=a1 qn﹣1;
(3)∵等比数列的公比q=5,第二项为10,
∴a1==2,a5=a1 q4=2×54=1250.
故答案为:(1)2;16;(2)an=a1 qn﹣1.
五、解答题(共2小题,每小题10分,共20分)
19.某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升(0≤x≤a)时,满足y=2x,下降时,y与x成反比.
(1)求a的值,并求当a≤x≤8时,y与x的函数表达式;
(2)若血液中药物浓度不低于3微克/毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
【分析】(1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)把y=3分别代入正比例函数和反比例函数解析式求出自变量的值,进而得出答案.
解:(1)有图象知,a=3;
又由题意可知:当3≤x≤8时,y与x成反比,设.
由图象可知,当x=3时,y=6,
∴m=3×6=18;
∴y=(3≤x≤8);
(2)把y=3分别代入y=2x和y=得,x=1.5和x=6,
∵6﹣1.5=4.5>4,
∴抗菌新药可以作为有效药物投入生产.
20.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
【分析】(1)根据CE=CF,列出方程即可解决问题;
(2)分两种情形分别讨论即可①当=时,△ECF∽△ADC,②当=时,△FCE∽△ADC;
解:(1)当CE=CF时,△CEF是等腰三角形,
∴4t=12﹣2t,
∴t=2.
(2)①当=时,△ECF∽△ADC,
∴=,
∴t=3.
②当=时,△FCE∽△ADC,
∴=,
∴t=,
综上所述,当t=s或3s时,以点E,C,F为顶点的三角形与△ACD相似.
六、(本大题12分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:△ADE∽△ACB;
(2)求证:DE=CE.
【分析】(1)由题可知∠ABE∽△ACD,所以,即,又∠A=∠A,所以△ADE∽△ACB;
(2)由(1)知∠AED=∠ABC,结合三角形外角的性质定理及平分线的性质可得∠CDE=∠ABE+∠ACD,可得结论.
【解答】证明:(1)如图,∵∠A=∠A,∠ABE=∠ACD,
∴△ABE∽△ACD,
∴,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB;
(2)由(1)知,△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠CBE+∠ABE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE+∠ACD,
∴DE=CE.
七、(本大题12分)
22.若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
【分析】(1)只需任选一个点作为顶点,同号两数作为二次项的系数,用顶点式表示两个为“同簇二次函数”的函数表达式即可.
(2)由y1的图象经过点A(1,1)可以求出m的值,然后根据y1+y2与y1为“同簇二次函数”就可以求出函数y2的表达式,然后将函数y2的表达式转化为顶点式,在利用二次函数的性质就可以解决问题.
解:(1)设顶点为(h,k)的二次函数的关系式为y=a(x﹣h)2+k,
当a=2,h=3,k=4时,
二次函数的关系式为y=2(x﹣3)2+4.
∵2>0,
∴该二次函数图象的开口向上.
当a=3,h=3,k=4时,
二次函数的关系式为y=3(x﹣3)2+4.
∵3>0,
∴该二次函数图象的开口向上.
∵两个函数y=2(x﹣3)2+4与y=3(x﹣3)2+4顶点相同,开口都向上,
∴两个函数y=2(x﹣3)2+4与y=3(x﹣3)2+4是“同簇二次函数”.
∴符合要求的两个“同簇二次函数”可以为:y=2(x﹣3)2+4与y=3(x﹣3)2+4(答案不唯一).
(2)∵y1的图象经过点A(1,1),
∴2×12﹣4×m×1+2m2+1=1.
整理得:m2﹣2m+1=0.
解得:m1=m2=1.
∴y1=2x2﹣4x+3
=2(x﹣1)2+1.
∴y1+y2=2x2﹣4x+3+ax2+bx+5
=(a+2)x2+(b﹣4)x+8
∵y1+y2与y1为“同簇二次函数”,
∴y1+y2=(a+2)(x﹣1)2+1
=(a+2)x2﹣2(a+2)x+(a+2)+1.
其中a+2>0,即a>﹣2.
∴.
解得:.
∴函数y2的表达式为:y2=5x2﹣10x+5.
∴y2=5x2﹣10x+5
=5(x﹣1)2.
∴函数y2的图象的对称轴为x=1.
∵5>0,
∴函数y2的图象开口向上.
①当0≤x≤1时,∵函数y2的图象开口向上,
∴y2随x的增大而减小,
∴当x=0时,y2取最大值,最大值为5×(0﹣1)2=5,
②当1≤x≤3时,∵函数y2的图象开口向上,
∴y2随x的增大而增大,
∴当x=3时,y2取最大值,
最大值为5(3﹣1)2=20.
综上所述:当0≤x≤3时,y2的最大值为20.
八、(本大题14分)
23.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE.
(1)求证:DH=CE;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当=时,值为 .(直接写答案)
【分析】(1)可得∠CHD=∠BEC,根据AAS可证明△DHC≌△CEB,即可求解;
(2))由△DHC≌△CEB,及DH∥BC,可得==,则GC=2GH,可求出GH的长;
(3)设S△DGH=16a,则S△BCG=49a,S△DCG=28a,求出S1和S2即可得出答案.
【解答】(1)证明:∵四边形ABCD是正方形,
∴CD=BC,∠HDC=∠BCE=90°,
∴∠DHC+∠DCH=90°,
∵CH⊥BE,
∴∠EFC=90°,
∴∠ECF+∠BEC=90°,
∴∠CHD=∠BEC,
在△DHC和△CEB中,
,
∴△DHC≌△CEB(AAS),
∴DH=CE;
(2)解:∵△DHC≌△CEB,
∴CH=BE,DH=CE,
∵点E是CD的中点,
∴CE=DE=CD,
∵CD=CB,
∴DH=BC,
∵DH∥BC,
∴==,
∴CG=2GH,
设GH=x,则CG=2x,
∴3x=8,
∴x=
即GH=;
(3)解:当的值为时,则=,
∵DH=CE,DC=BC,
∴=,
∵DH∥BC,
∴==,
∴=,=,
设S△DGH=16a,则S△BCG=49a,S△DCG=28a,
∴S△BCD=49a+28a=77a,
∴S1=2S△BCD=154a,
∵S△DEG:S△CEG=3:4,
∴S△DEG=12a,
∴S2=16a+12a=28a,
∴==,
故答案为:.
同课章节目录
