2020-2021学年山东省聊城市莘县俎店中学七年级(上)第二次月考数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省聊城市莘县俎店中学七年级(上)第二次月考数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 710.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览



文档简介
2020-2021学年山东省聊城市莘县俎店中学七年级第一学期第二次月考数学试卷
一、选择题(本题共12个小题;每小题3分,共36分)
1.在|﹣2|,﹣(﹣2),﹣22,(﹣2)2,这四个数中,最小的有理数是( )
A.|﹣2| B.﹣(﹣2) C.﹣22 D.(﹣2)2
2.有理数a,b在数轴上的位置如图所示,则在下列结论中正确的是( )
A.a+b<0 B.a﹣b<0 C.a<﹣b D.|a|>|b|
3.下列说法中正确的是( )
A.经过一点有且只有一条直线
B.连接两点的线段叫做两点之间的距离
C.射线比直线短
D.A,B,C三点在同一直线上且AB=BC,则B是线段AC的中点
4.悉尼、伦敦与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市 悉尼 伦敦
时差/时 +2 ﹣8
当北京12月12日23时,悉尼、伦敦的时间分别是( )
A.12月13日1时;12月12日15时
B.12月13日1时;12月11日15时
C.12月12日21时;12月12日15时
D.12月12日21时;12月13日7时
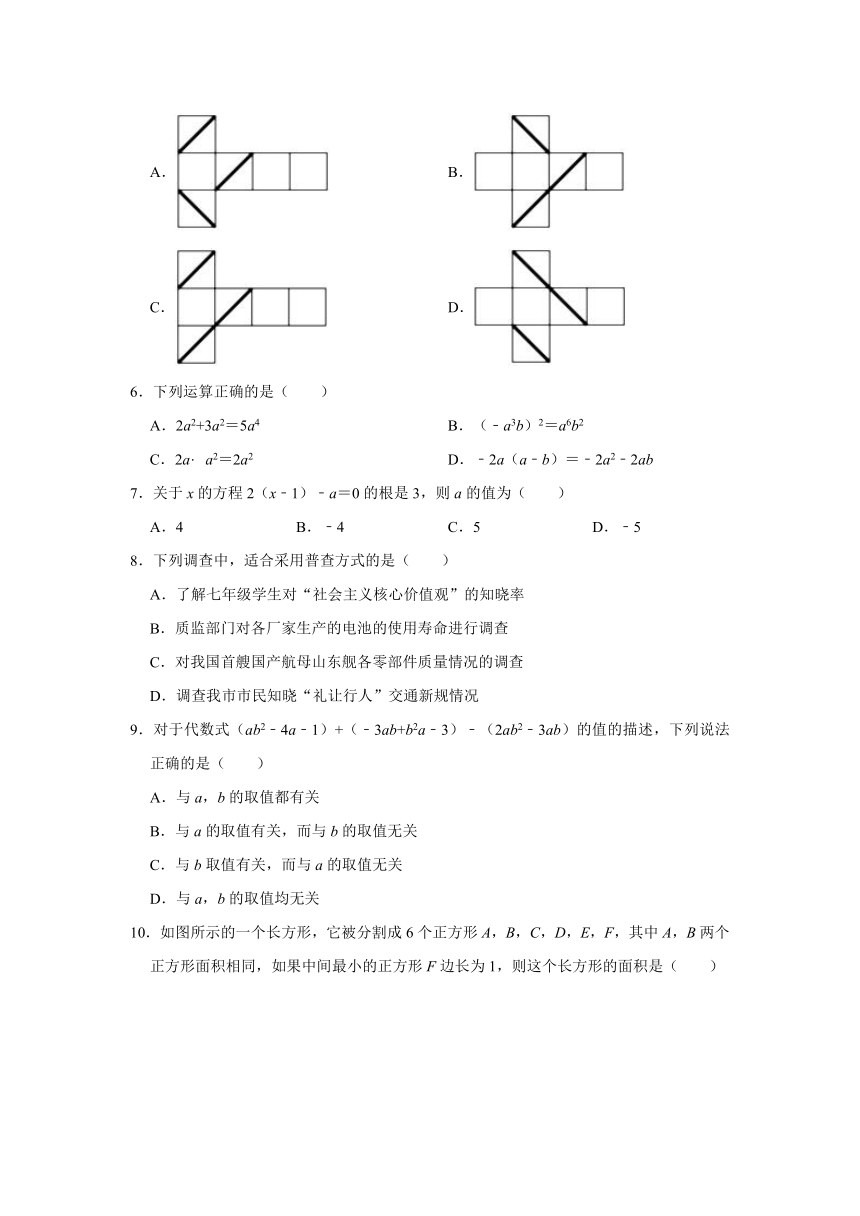
5.如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开,外表面朝上,展开图可能是( )
A. B.
C. D.
6.下列运算正确的是( )
A.2a2+3a2=5a4 B.(﹣a3b)2=a6b2
C.2a a2=2a2 D.﹣2a(a﹣b)=﹣2a2﹣2ab
7.关于x的方程2(x﹣1)﹣a=0的根是3,则a的值为( )
A.4 B.﹣4 C.5 D.﹣5
8.下列调查中,适合采用普查方式的是( )
A.了解七年级学生对“社会主义核心价值观”的知晓率
B.质监部门对各厂家生产的电池的使用寿命进行调查
C.对我国首艘国产航母山东舰各零部件质量情况的调查
D.调查我市市民知晓“礼让行人”交通新规情况
9.对于代数式(ab2﹣4a﹣1)+(﹣3ab+b2a﹣3)﹣(2ab2﹣3ab)的值的描述,下列说法正确的是( )
A.与a,b的取值都有关
B.与a的取值有关,而与b的取值无关
C.与b取值有关,而与a的取值无关
D.与a,b的取值均无关
10.如图所示的一个长方形,它被分割成6个正方形A,B,C,D,E,F,其中A,B两个正方形面积相同,如果中间最小的正方形F边长为1,则这个长方形的面积是( )
A.123 B.142 C.143 D.144
11.甲乙两桶共有48千克水,如果甲桶给乙桶加乙桶水的一倍,然后乙桶又给甲桶加甲桶剩水的一倍,那么两桶水的质量相等,问原来甲、乙两桶内各有多少千克水?若设原来乙桶内水的质量为x千克,则可列方程为( )
A.2(48﹣x﹣x)=(x+x)﹣(48﹣x﹣x)
B.2[x﹣(48﹣x)]=2(48﹣x)﹣[x﹣(48﹣x)]
C.2(48﹣x﹣x)=(x+48﹣x)﹣(48﹣x﹣x)
D.(48﹣x﹣x)+(x+x)=(x+48﹣x)﹣(48﹣x﹣x)
12.想象有一条很长的绳子可以绕地球赤道一圈,且绳子与地球之间的间隙是p厘米,设地球半径为d千米,则绳子的长度比地球赤道的长度长( )
A.[2π(d+p)﹣2πd]厘米 B.(2πd﹣2πp)厘米
C.2πd厘米 D.2πp厘米
二、填空题(本题共6个小题;每小题3分,共18分)
13.已知|a﹣4|+(2b+1)2=0,则a﹣b= .
14.已知a﹣2b=﹣,则代数式2a﹣4b+1的值是 .
15.中国互联网络信息中心数据显示,截至2019年6月,我国网络购物用户规模达6.39亿,较2018年底增长2871万,占网民整体的74.8%,2871万用科学记数法表示为 .
16.如图,将一根绳子对折以后用线段AB表示,现从点C处将绳子剪断,剪断后的各段绳子中最长的一段为60cm,且AC=BC,则这条绳子的原长为 .
17.为了加强公民节水意识,合理利用水资源,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定立方米及以下的部分和超出部分标准不同.下表反映的是小亮家1﹣4月份用水量与应交水费情况:
月份 1 2 3 4
用水量(m3) 6 8 10 12
费用(元) 9 12 18 24
小亮家12月份用水xm3(12月份用水量超过规定用水量),应交水费y元,则y关于x的函数关系式是 .
18.有一系列方程,第1个方程是﹣(x﹣2)=1,解为x=;第2个方程是﹣(x﹣3)=1,解为x=;第3个方程是﹣(x﹣4)=1,解为x=,…,根据规律第7个方程﹣(x﹣8)=1,解为 .
三、解答题(本题共7个大题,共66分,解答应写出文字说明或推演步骤)
19.计算:
(1)×(﹣25)﹣(﹣25)×+(﹣25)÷8;
(2)﹣12019﹣0.54×25+32×(﹣)5.
20.解方程:
(1)2(3x﹣4)﹣3(4+3x)=4x﹣7(5﹣2x);
(2)x﹣=.
21.(1)化简求值:已知:A=a2﹣3ab﹣2b2,B=a2﹣6ab+2b2,且a=,|b|=1,求3A﹣2B的值;
(2)已知关于字母x,y的多项式x2﹣3kxy﹣5y2﹣(﹣2xy﹣7)化简后不含xy项,求k的值.
22.“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
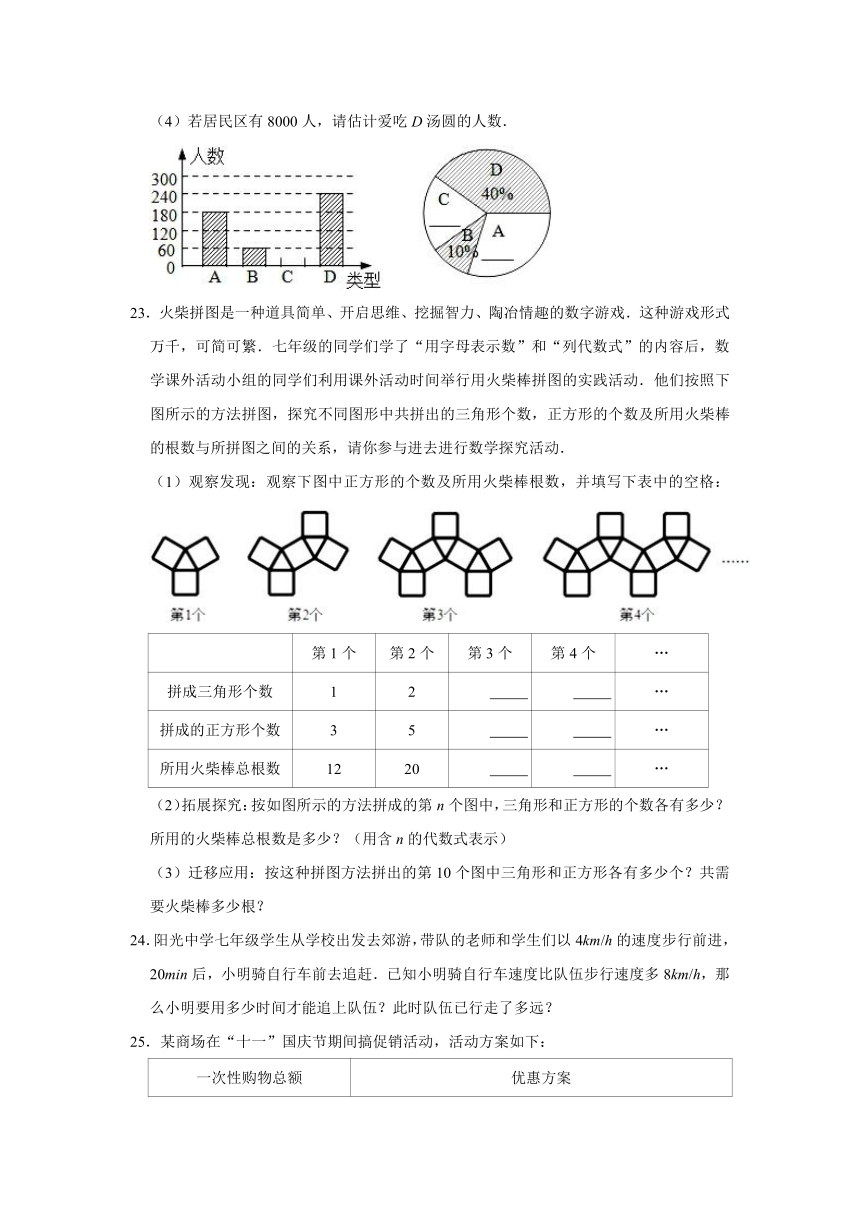
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
23.火柴拼图是一种道具简单、开启思维、挖掘智力、陶冶情趣的数字游戏.这种游戏形式万千,可简可繁.七年级的同学们学了“用字母表示数”和“列代数式”的内容后,数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动.他们按照下图所示的方法拼图,探究不同图形中共拼出的三角形个数,正方形的个数及所用火柴棒的根数与所拼图之间的关系,请你参与进去进行数学探究活动.
(1)观察发现:观察下图中正方形的个数及所用火柴棒根数,并填写下表中的空格:
第1个 第2个 第3个 第4个 …
拼成三角形个数 1 2 …
拼成的正方形个数 3 5 …
所用火柴棒总根数 12 20 …
(2)拓展探究:按如图所示的方法拼成的第n个图中,三角形和正方形的个数各有多少?所用的火柴棒总根数是多少?(用含n的代数式表示)
(3)迁移应用:按这种拼图方法拼出的第10个图中三角形和正方形各有多少个?共需要火柴棒多少根?
24.阳光中学七年级学生从学校出发去郊游,带队的老师和学生们以4km/h的速度步行前进,20min后,小明骑自行车前去追赶.已知小明骑自行车速度比队伍步行速度多8km/h,那么小明要用多少时间才能追上队伍?此时队伍已行走了多远?
25.某商场在“十一”国庆节期间搞促销活动,活动方案如下:
一次性购物总额 优惠方案
不超过500元 不给予优惠
超过500元,但不超过800元 8折优惠
超过800元 其中800元给予8折优惠,超过800元的部分给予6折优惠
小莹的妈妈在促销期间,两次购物分别支付了360元和880元.
(1)小莹的妈妈两次购买的商品如果不打折,应支付多少钱?在此活动中,她节省了多少钱?
(2)若两次购物一起支付,则小莹的妈妈只需付款多少元?
参考答案
一、选择题(本题共12个小题;每小题3分,共36分)
1.在|﹣2|,﹣(﹣2),﹣22,(﹣2)2,这四个数中,最小的有理数是( )
A.|﹣2| B.﹣(﹣2) C.﹣22 D.(﹣2)2
【分析】根据有理数的大小比较法则:正数都大于0,负数都小于0,正数大于一切负数,两个负数比较大小,绝对值大的反而小;容易得出结果.
解:|﹣2|=2,﹣(﹣2)=2,﹣22=﹣4,(﹣2)2=4,
∴﹣22<|﹣2|=﹣(﹣2)<(﹣2)2,
∴在|﹣2|,﹣(﹣2),﹣22,(﹣2)2,这四个数中,最小的有理数是﹣22,
故选:C.
2.有理数a,b在数轴上的位置如图所示,则在下列结论中正确的是( )
A.a+b<0 B.a﹣b<0 C.a<﹣b D.|a|>|b|
【分析】利用数轴先判断出a、b的正负情况以及它们绝对值的大小,然后再进行比较即可.
解:由a、b在数轴上的位置可知:﹣1<a<0<1<b,且|a|<|b|,
∴a+b>0,故A选项不符合题意;
a﹣b<0,故B选项符合题意;
a>﹣b.故C选项不符合题意;
|a|<|b|,故D选项不符合题意;
故选:B.
3.下列说法中正确的是( )
A.经过一点有且只有一条直线
B.连接两点的线段叫做两点之间的距离
C.射线比直线短
D.A,B,C三点在同一直线上且AB=BC,则B是线段AC的中点
【分析】根据直线的性质,两点间距离的概念,射线与直线的意义,线段中点的概念,对各小题逐一分析判断后,利用排除法求解.
解:A.经过一点有无数条直线,故本小题错误;
B.应为连接两点的线段的长度叫做两点的距离,故本小题错误;
C.射线与直线不能比较长短,故本小题错误;
D.因为A、B、C三点在同一直线上,且AB=BC,所以点B是线段AC的中点,故本小题正确;
故选:D.
4.悉尼、伦敦与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市 悉尼 伦敦
时差/时 +2 ﹣8
当北京12月12日23时,悉尼、伦敦的时间分别是( )
A.12月13日1时;12月12日15时
B.12月13日1时;12月11日15时
C.12月12日21时;12月12日15时
D.12月12日21时;12月13日7时
【分析】由统计表得出:悉尼时间比北京时间早2小时,也就是12月13日1时.伦敦比北京时间要晚8个小时,也就是12月12日15时.
解:悉尼的时间是:12月12日23时+2小时=12月13日1时,
伦敦时间是:12月12日23时﹣8小时=12月12日15时.
故选:A.
5.如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开,外表面朝上,展开图可能是( )
A. B.
C. D.
【分析】根据正方体的表面展开图进行分析解答即可.
解:根据正方体的表面展开图可得,展开图可能是:
或
故选:A.
6.下列运算正确的是( )
A.2a2+3a2=5a4 B.(﹣a3b)2=a6b2
C.2a a2=2a2 D.﹣2a(a﹣b)=﹣2a2﹣2ab
【分析】直接利用合并同类项法则以及积的乘方运算法则、单项式乘单项式、单项式乘多项式运算法则,分别判断得出答案.
解:A.2a2+3a2=5a2,故此选项不合题意;
B.(﹣a3b)2=a6b2,故此选项符合题意;
C.2a a2=2a3,故此选项不合题意;
D.﹣2a(a﹣b)=﹣2a2+2ab,故此选项不合题意;
故选:B.
7.关于x的方程2(x﹣1)﹣a=0的根是3,则a的值为( )
A.4 B.﹣4 C.5 D.﹣5
【分析】虽然是关于x的方程,但是含有两个未知数,其实质是知道一个未知数的值求另一个未知数的值.
解:把x=3代入2(x﹣1)﹣a=0中:
得:2(3﹣1)﹣a=0
解得:a=4
故选:A.
8.下列调查中,适合采用普查方式的是( )
A.了解七年级学生对“社会主义核心价值观”的知晓率
B.质监部门对各厂家生产的电池的使用寿命进行调查
C.对我国首艘国产航母山东舰各零部件质量情况的调查
D.调查我市市民知晓“礼让行人”交通新规情况
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
解:A.了解七年级学生对“社会主义核心价值观”的知晓率,适合采用抽样调查方式,故本选项不符合题意;
B.质监部门对各厂家生产的电池的使用寿命进行调查,适合采用抽样调查方式,故本选项不符合题意;
C.对我国首艘国产航母山东舰各零部件质量情况的调查,适合采用全面调查方式,故本选项符合题意;
D.调查我市市民知晓“礼让行人”交通新规情况,适合采用抽样调查方式,故本选项不符合题意;
故选:C.
9.对于代数式(ab2﹣4a﹣1)+(﹣3ab+b2a﹣3)﹣(2ab2﹣3ab)的值的描述,下列说法正确的是( )
A.与a,b的取值都有关
B.与a的取值有关,而与b的取值无关
C.与b取值有关,而与a的取值无关
D.与a,b的取值均无关
【分析】原式去括号合并得到最简结果,判断即可.
解:(ab2﹣4a﹣1)+(﹣3ab+b2a﹣3)﹣(2ab2﹣3ab)
=ab2﹣4a﹣1﹣3ab+b2a﹣3﹣2ab2+3ab
=﹣4a﹣4,
则代数式的值与与a的取值有关,而与b的取值无关.
故选:B.
10.如图所示的一个长方形,它被分割成6个正方形A,B,C,D,E,F,其中A,B两个正方形面积相同,如果中间最小的正方形F边长为1,则这个长方形的面积是( )
A.123 B.142 C.143 D.144
【分析】设正方形C的边长为x,则正方形E的边长为(x+1),正方形B的边长为(2x﹣1),正方形F的边长为(x+2),由长方形的对边相等,即可得出关于x的一元一次方程,解之即可得出x的值,再利用长方形的面积公式即可求出结论.
解:设正方形C的边长为x,则正方形E的边长为(x+1),正方形B的边长为(2x﹣1),正方形F的边长为(x+2),
依题意,得:x+(2x﹣1)=(x+1)+(x+2),
解得:x=4,
∴S=[x+x+(x+1)] [(x+1)+(x+2)]=13×11=143.
故选:C.
11.甲乙两桶共有48千克水,如果甲桶给乙桶加乙桶水的一倍,然后乙桶又给甲桶加甲桶剩水的一倍,那么两桶水的质量相等,问原来甲、乙两桶内各有多少千克水?若设原来乙桶内水的质量为x千克,则可列方程为( )
A.2(48﹣x﹣x)=(x+x)﹣(48﹣x﹣x)
B.2[x﹣(48﹣x)]=2(48﹣x)﹣[x﹣(48﹣x)]
C.2(48﹣x﹣x)=(x+48﹣x)﹣(48﹣x﹣x)
D.(48﹣x﹣x)+(x+x)=(x+48﹣x)﹣(48﹣x﹣x)
【分析】设甲桶内原有水xkg,则乙桶内原有水(48﹣x)kg,若乙桶的水增加1倍,则甲桶给乙桶加(48﹣x)kg水,此时甲桶有x﹣(48﹣x),然后用同样的方法解决乙桶给甲桶加水,为甲桶剩余的水的一倍的问题,最后利用两桶内水的质量相等列方程2(2x﹣48)=2(48﹣x)﹣(2x﹣48),再解方程求出x后计算48﹣x即可.
解:设甲桶内原有水xkg,则乙桶内原有水(48﹣x)kg,
根据题意得2(2x﹣48)=2(48﹣x)﹣(2x﹣48),
故选:B.
12.想象有一条很长的绳子可以绕地球赤道一圈,且绳子与地球之间的间隙是p厘米,设地球半径为d千米,则绳子的长度比地球赤道的长度长( )
A.[2π(d+p)﹣2πd]厘米 B.(2πd﹣2πp)厘米
C.2πd厘米 D.2πp厘米
【分析】由题知绳子的长度是2π(d×105+p)厘米,地球赤道的长度为2πd×105厘米,故绳子的长度比地球赤道的长度长2π(d×105+p)﹣2πd×105=2πp厘米.
解:由题知,d千米=d×105厘米,
∴绳子的长度是2π(d×105+p) 厘米,
地球赤道的长度为2πd×105厘米,
故绳子的长度比地球赤道的长度长2π(d×105+p)﹣2πd×105=2πp厘米,
故选:D.
二、填空题(本题共6个小题;每小题3分,共18分)
13.已知|a﹣4|+(2b+1)2=0,则a﹣b= .
【分析】直接利用绝对值和偶次方非负数的性质得出a,b的值,进而得出答案.
解:∵|a﹣4|+(2b+1)2=0,而|a﹣4|≥0,(2b+1)2≥0,
∴a﹣4=0,2b+1=0,
解得a=4,b=,
∴=.
故答案为:.
14.已知a﹣2b=﹣,则代数式2a﹣4b+1的值是 ﹣ .
【分析】将代数式2a﹣4b+1变形为2(a﹣2b)+1,将a﹣2b=﹣带入即可.
解:∵a﹣2b=﹣,
∴2a﹣4b+1=2(a﹣2b)+1=2×+1=﹣,
故答案为:﹣.
15.中国互联网络信息中心数据显示,截至2019年6月,我国网络购物用户规模达6.39亿,较2018年底增长2871万,占网民整体的74.8%,2871万用科学记数法表示为 2.871×107 .
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,且n比原来的整数位数少1,据此判断即可.
解:2871万=28710000=2.871×107.
故答案为:2.871×107.
16.如图,将一根绳子对折以后用线段AB表示,现从点C处将绳子剪断,剪断后的各段绳子中最长的一段为60cm,且AC=BC,则这条绳子的原长为 80cm或240cm .
【分析】根据绳子对折以后用线段AB表示,可得绳长是AB的2倍,分类讨论,CB的2倍最长,可得CB,AC的2倍最长,可得AC的长,再根据线段间的比例关系,可得答案.
解:当CB的2倍最长时,得
CB=30cm,
AC=CB=10cm,
AB=AC+CB=40cm,
这条绳子的原长为2AB=80cm;
当AC的2倍最长时,得
AC=30cm,AC=CB,
CB=3AC=90cm,
AB=AC+CB=120cm,
这条绳子的原长为2AB=240cm.
故答案为:80cm或240cm.
17.为了加强公民节水意识,合理利用水资源,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定立方米及以下的部分和超出部分标准不同.下表反映的是小亮家1﹣4月份用水量与应交水费情况:
月份 1 2 3 4
用水量(m3) 6 8 10 12
费用(元) 9 12 18 24
小亮家12月份用水xm3(12月份用水量超过规定用水量),应交水费y元,则y关于x的函数关系式是 y=3x﹣12(x>8) .
【分析】根据表格判断出1,2月份未超过用水量,3,4月份超过用水量,然后通过待定系数法求解.
解:由题得1﹣2月用水量增加2m3,水费增加3元,2﹣3月,3﹣4月水量增加2m3,水费增加6元,
∴1,2月y与x的关系式为设y=kx+b,
把x=6,y=9和x=8,y=12代入y=kx+b得,
解得,
∴y=x(0≤x≤8).
设3,4月份y与x的关系为y=mx+n,
把x=10,y=18和x=12,y=24代入y=mx+n得,
解得,
∴y=3x﹣12(x>8).
∵12月用水量超过规定用水量,
故答案为:y=3x﹣12(x>8).
18.有一系列方程,第1个方程是﹣(x﹣2)=1,解为x=;第2个方程是﹣(x﹣3)=1,解为x=;第3个方程是﹣(x﹣4)=1,解为x=,…,根据规律第7个方程﹣(x﹣8)=1,解为 x= .
【分析】根据已知三个方程的特点及解的特点得到一般性规律,即可确定出第7个方程的解.
解:根据题意得到第n个方程为,解为:x=(n为正整数),
∴第7个方程﹣(x﹣8)=1,解为=.
故答案为:x=.
三、解答题(本题共7个大题,共66分,解答应写出文字说明或推演步骤)
19.计算:
(1)×(﹣25)﹣(﹣25)×+(﹣25)÷8;
(2)﹣12019﹣0.54×25+32×(﹣)5.
【分析】(1)将除法转化为乘法,再逆用乘法分配律进一步计算即可;
(2)先计算乘方,再进一步计算即可.
解:(1)原式=×(﹣25)﹣(﹣25)×+(﹣25)×
=(﹣25)×(++)
=(﹣25)×
=﹣;
(2)原式=﹣1﹣(0.5×2)4×2+32×(﹣)
=﹣1﹣2﹣1
=﹣4.
20.解方程:
(1)2(3x﹣4)﹣3(4+3x)=4x﹣7(5﹣2x);
(2)x﹣=.
【分析】(1)方程去括号,移项合并,把未知数系数化为1,求出解即可;
(2)方程去分母,去括号,移项合并,把未知数系数化为1,求出解即可.
解:(1)2(3x﹣4)﹣3(4+3x)=4x﹣7(5﹣2x),
去括号,得6x﹣8﹣12﹣9x=4x﹣35+14x,
移项,得6x﹣9x﹣4x﹣14x=8+12﹣35,
合并同类项,得﹣21x=﹣15,
系数化为1,得;
(2)x﹣=,
去分母,得12x﹣4(1﹣4x)=3(11x+7),
去括号,得12x﹣4+16x=33x+21,
移项,得12x+16x﹣33x=21+4,
合并同类项,得﹣5x=25,
系数化为1,得x=﹣5.
21.(1)化简求值:已知:A=a2﹣3ab﹣2b2,B=a2﹣6ab+2b2,且a=,|b|=1,求3A﹣2B的值;
(2)已知关于字母x,y的多项式x2﹣3kxy﹣5y2﹣(﹣2xy﹣7)化简后不含xy项,求k的值.
【分析】(1)根据整式的加减运算法则进行化简,然后将a与b的值代入原式即可求出答案.
(2)根据整式的加减运算法则进行化简,然后令含xy的项的系数之和为0即可求出k的值.
解:(1)3A﹣2B
=3(a2﹣3ab﹣2b2)﹣2(a2﹣6ab+2b2)
=3a2﹣9ab﹣6b2﹣2a2+12ab﹣4b2
=a2+3ab﹣10b2,
由题意可知:a=,b=±1,
当a=,b=1时,
原式=+3××1﹣10×1
=+﹣10
=.
当a=,b=﹣1时,
原式=﹣3××1﹣10×1
=﹣﹣10
=.
(2)原式=x2﹣3kxy﹣5y2+2xy+7
=x2+(2﹣3k)xy﹣5y2+7,
令2﹣3k=0,
∴k=.
22.“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 600 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
【分析】(1)由B的人数除以占的百分比求出调查的人数即可;
(2)求出C的人数与百分比,A的百分比,补全两个图形即可;
(3)由A的百分比乘以360即可得到结果;
(4)由D的百分比乘以8000即可得到结果.
解:(1)本次参加抽样调查的居民的人数是:60÷10%=600(人);
故答案为:600;
(2)由题意得:C的人数为600﹣(180+60+240)=600﹣480=120(人),C的百分比为120÷600×100%=20%;A的百分比为180÷600×100%=30%;
(3)根据题意得:360°×30%=108°,
图②中表示“A”的圆心角的度数108°;
(4)8000×40%=3200(人),
即爱吃D汤圆的人数约为3200人.
23.火柴拼图是一种道具简单、开启思维、挖掘智力、陶冶情趣的数字游戏.这种游戏形式万千,可简可繁.七年级的同学们学了“用字母表示数”和“列代数式”的内容后,数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动.他们按照下图所示的方法拼图,探究不同图形中共拼出的三角形个数,正方形的个数及所用火柴棒的根数与所拼图之间的关系,请你参与进去进行数学探究活动.
(1)观察发现:观察下图中正方形的个数及所用火柴棒根数,并填写下表中的空格:
第1个 第2个 第3个 第4个 …
拼成三角形个数 1 2 3 4 …
拼成的正方形个数 3 5 7 9 …
所用火柴棒总根数 12 20 28 36 …
(2)拓展探究:按如图所示的方法拼成的第n个图中,三角形和正方形的个数各有多少?所用的火柴棒总根数是多少?(用含n的代数式表示)
(3)迁移应用:按这种拼图方法拼出的第10个图中三角形和正方形各有多少个?共需要火柴棒多少根?
【分析】(1)观察图形的变化即可完成填空;
(2)结合(1)即可得第n个图形的三角形和正方形的个数以及火柴棒个数;
(3)把n=10代入可得答案.
解:(1)第3个图形中,拼成三角形的个数是3个,拼成正方形的个数是7个,所用火柴棒总根数是28根;
第4个图形中,拼成三角形的个数是4个,拼成正方形的个数是9个,所用火柴棒总根数是36根;
故答案为:3,7,28;4,9,36.
(2)由(1)可得,
第n个图形中,拼成三角形的个数是n个,拼成正方形的个数是(2n+1)个,所用火柴棒总根数是(8n+4)根.
(3)当n=10时,拼成三角形的个数是10个,
拼成正方形的个数是2×10+1=21(个),
所用火柴棒总根数是8×10+4=84(根).
24.阳光中学七年级学生从学校出发去郊游,带队的老师和学生们以4km/h的速度步行前进,20min后,小明骑自行车前去追赶.已知小明骑自行车速度比队伍步行速度多8km/h,那么小明要用多少时间才能追上队伍?此时队伍已行走了多远?
【分析】设小明要用xh才能追上队伍,则队伍行走的时间是(x+)h.根据他们所行驶的路程相等列出方程并求得x的值;然后根据路程=时间×速度计算队伍行走的路程.
解:设小明要用xh才能追上队伍,则队伍行走的时间是(x+)h,
根据题意,得4(x+)=(4+8)x,
解得x=.
所以4(x+)=4(+)=2.
答:小明要用小时才能追上队伍,此时队伍已行走了2km.
25.某商场在“十一”国庆节期间搞促销活动,活动方案如下:
一次性购物总额 优惠方案
不超过500元 不给予优惠
超过500元,但不超过800元 8折优惠
超过800元 其中800元给予8折优惠,超过800元的部分给予6折优惠
小莹的妈妈在促销期间,两次购物分别支付了360元和880元.
(1)小莹的妈妈两次购买的商品如果不打折,应支付多少钱?在此活动中,她节省了多少钱?
(2)若两次购物一起支付,则小莹的妈妈只需付款多少元?
【分析】(1)由500×0.8=400,360<400,可知第一次购买的商品如果不打折,应支付360元,而超过500元,但不超过800元的8折优惠,超过800元的,800元给予8折优惠,超过800元的部分给予6折优惠,可知第二次购买的商品如果不打折,应支付1200元,即得小莹的妈妈两次购买的商品如果不打折,应支付1560元,她节省了320元;
(2)根据800元给予8折优惠,超过800元的部分给予6折优惠,即可得两次购物一起支付,小莹的妈妈付款为1096元.
解:(1)∵500×0.8=400,360<400,
∴支付了360元,商品没打折,即第一次购买的商品如果不打折,应支付360元,
∵800×0.8=640,880﹣640=240,240÷0.6=400,800+400=1200,
∴第二次购买的商品如果不打折,应支付1200元,
∴小莹的妈妈两次购买的商品如果不打折,应支付1560元,
而1560﹣(360+880)=320,
∴在此活动中,她节省了320元;
(2)800×0.8+(1560﹣800)×0.6=1096(元),
∴若两次购物一起支付,则小莹的妈妈只需付款1096元.
一、选择题(本题共12个小题;每小题3分,共36分)
1.在|﹣2|,﹣(﹣2),﹣22,(﹣2)2,这四个数中,最小的有理数是( )
A.|﹣2| B.﹣(﹣2) C.﹣22 D.(﹣2)2
2.有理数a,b在数轴上的位置如图所示,则在下列结论中正确的是( )
A.a+b<0 B.a﹣b<0 C.a<﹣b D.|a|>|b|
3.下列说法中正确的是( )
A.经过一点有且只有一条直线
B.连接两点的线段叫做两点之间的距离
C.射线比直线短
D.A,B,C三点在同一直线上且AB=BC,则B是线段AC的中点
4.悉尼、伦敦与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市 悉尼 伦敦
时差/时 +2 ﹣8
当北京12月12日23时,悉尼、伦敦的时间分别是( )
A.12月13日1时;12月12日15时
B.12月13日1时;12月11日15时
C.12月12日21时;12月12日15时
D.12月12日21时;12月13日7时
5.如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开,外表面朝上,展开图可能是( )
A. B.
C. D.
6.下列运算正确的是( )
A.2a2+3a2=5a4 B.(﹣a3b)2=a6b2
C.2a a2=2a2 D.﹣2a(a﹣b)=﹣2a2﹣2ab
7.关于x的方程2(x﹣1)﹣a=0的根是3,则a的值为( )
A.4 B.﹣4 C.5 D.﹣5
8.下列调查中,适合采用普查方式的是( )
A.了解七年级学生对“社会主义核心价值观”的知晓率
B.质监部门对各厂家生产的电池的使用寿命进行调查
C.对我国首艘国产航母山东舰各零部件质量情况的调查
D.调查我市市民知晓“礼让行人”交通新规情况
9.对于代数式(ab2﹣4a﹣1)+(﹣3ab+b2a﹣3)﹣(2ab2﹣3ab)的值的描述,下列说法正确的是( )
A.与a,b的取值都有关
B.与a的取值有关,而与b的取值无关
C.与b取值有关,而与a的取值无关
D.与a,b的取值均无关
10.如图所示的一个长方形,它被分割成6个正方形A,B,C,D,E,F,其中A,B两个正方形面积相同,如果中间最小的正方形F边长为1,则这个长方形的面积是( )
A.123 B.142 C.143 D.144
11.甲乙两桶共有48千克水,如果甲桶给乙桶加乙桶水的一倍,然后乙桶又给甲桶加甲桶剩水的一倍,那么两桶水的质量相等,问原来甲、乙两桶内各有多少千克水?若设原来乙桶内水的质量为x千克,则可列方程为( )
A.2(48﹣x﹣x)=(x+x)﹣(48﹣x﹣x)
B.2[x﹣(48﹣x)]=2(48﹣x)﹣[x﹣(48﹣x)]
C.2(48﹣x﹣x)=(x+48﹣x)﹣(48﹣x﹣x)
D.(48﹣x﹣x)+(x+x)=(x+48﹣x)﹣(48﹣x﹣x)
12.想象有一条很长的绳子可以绕地球赤道一圈,且绳子与地球之间的间隙是p厘米,设地球半径为d千米,则绳子的长度比地球赤道的长度长( )
A.[2π(d+p)﹣2πd]厘米 B.(2πd﹣2πp)厘米
C.2πd厘米 D.2πp厘米
二、填空题(本题共6个小题;每小题3分,共18分)
13.已知|a﹣4|+(2b+1)2=0,则a﹣b= .
14.已知a﹣2b=﹣,则代数式2a﹣4b+1的值是 .
15.中国互联网络信息中心数据显示,截至2019年6月,我国网络购物用户规模达6.39亿,较2018年底增长2871万,占网民整体的74.8%,2871万用科学记数法表示为 .
16.如图,将一根绳子对折以后用线段AB表示,现从点C处将绳子剪断,剪断后的各段绳子中最长的一段为60cm,且AC=BC,则这条绳子的原长为 .
17.为了加强公民节水意识,合理利用水资源,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定立方米及以下的部分和超出部分标准不同.下表反映的是小亮家1﹣4月份用水量与应交水费情况:
月份 1 2 3 4
用水量(m3) 6 8 10 12
费用(元) 9 12 18 24
小亮家12月份用水xm3(12月份用水量超过规定用水量),应交水费y元,则y关于x的函数关系式是 .
18.有一系列方程,第1个方程是﹣(x﹣2)=1,解为x=;第2个方程是﹣(x﹣3)=1,解为x=;第3个方程是﹣(x﹣4)=1,解为x=,…,根据规律第7个方程﹣(x﹣8)=1,解为 .
三、解答题(本题共7个大题,共66分,解答应写出文字说明或推演步骤)
19.计算:
(1)×(﹣25)﹣(﹣25)×+(﹣25)÷8;
(2)﹣12019﹣0.54×25+32×(﹣)5.
20.解方程:
(1)2(3x﹣4)﹣3(4+3x)=4x﹣7(5﹣2x);
(2)x﹣=.
21.(1)化简求值:已知:A=a2﹣3ab﹣2b2,B=a2﹣6ab+2b2,且a=,|b|=1,求3A﹣2B的值;
(2)已知关于字母x,y的多项式x2﹣3kxy﹣5y2﹣(﹣2xy﹣7)化简后不含xy项,求k的值.
22.“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
23.火柴拼图是一种道具简单、开启思维、挖掘智力、陶冶情趣的数字游戏.这种游戏形式万千,可简可繁.七年级的同学们学了“用字母表示数”和“列代数式”的内容后,数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动.他们按照下图所示的方法拼图,探究不同图形中共拼出的三角形个数,正方形的个数及所用火柴棒的根数与所拼图之间的关系,请你参与进去进行数学探究活动.
(1)观察发现:观察下图中正方形的个数及所用火柴棒根数,并填写下表中的空格:
第1个 第2个 第3个 第4个 …
拼成三角形个数 1 2 …
拼成的正方形个数 3 5 …
所用火柴棒总根数 12 20 …
(2)拓展探究:按如图所示的方法拼成的第n个图中,三角形和正方形的个数各有多少?所用的火柴棒总根数是多少?(用含n的代数式表示)
(3)迁移应用:按这种拼图方法拼出的第10个图中三角形和正方形各有多少个?共需要火柴棒多少根?
24.阳光中学七年级学生从学校出发去郊游,带队的老师和学生们以4km/h的速度步行前进,20min后,小明骑自行车前去追赶.已知小明骑自行车速度比队伍步行速度多8km/h,那么小明要用多少时间才能追上队伍?此时队伍已行走了多远?
25.某商场在“十一”国庆节期间搞促销活动,活动方案如下:
一次性购物总额 优惠方案
不超过500元 不给予优惠
超过500元,但不超过800元 8折优惠
超过800元 其中800元给予8折优惠,超过800元的部分给予6折优惠
小莹的妈妈在促销期间,两次购物分别支付了360元和880元.
(1)小莹的妈妈两次购买的商品如果不打折,应支付多少钱?在此活动中,她节省了多少钱?
(2)若两次购物一起支付,则小莹的妈妈只需付款多少元?
参考答案
一、选择题(本题共12个小题;每小题3分,共36分)
1.在|﹣2|,﹣(﹣2),﹣22,(﹣2)2,这四个数中,最小的有理数是( )
A.|﹣2| B.﹣(﹣2) C.﹣22 D.(﹣2)2
【分析】根据有理数的大小比较法则:正数都大于0,负数都小于0,正数大于一切负数,两个负数比较大小,绝对值大的反而小;容易得出结果.
解:|﹣2|=2,﹣(﹣2)=2,﹣22=﹣4,(﹣2)2=4,
∴﹣22<|﹣2|=﹣(﹣2)<(﹣2)2,
∴在|﹣2|,﹣(﹣2),﹣22,(﹣2)2,这四个数中,最小的有理数是﹣22,
故选:C.
2.有理数a,b在数轴上的位置如图所示,则在下列结论中正确的是( )
A.a+b<0 B.a﹣b<0 C.a<﹣b D.|a|>|b|
【分析】利用数轴先判断出a、b的正负情况以及它们绝对值的大小,然后再进行比较即可.
解:由a、b在数轴上的位置可知:﹣1<a<0<1<b,且|a|<|b|,
∴a+b>0,故A选项不符合题意;
a﹣b<0,故B选项符合题意;
a>﹣b.故C选项不符合题意;
|a|<|b|,故D选项不符合题意;
故选:B.
3.下列说法中正确的是( )
A.经过一点有且只有一条直线
B.连接两点的线段叫做两点之间的距离
C.射线比直线短
D.A,B,C三点在同一直线上且AB=BC,则B是线段AC的中点
【分析】根据直线的性质,两点间距离的概念,射线与直线的意义,线段中点的概念,对各小题逐一分析判断后,利用排除法求解.
解:A.经过一点有无数条直线,故本小题错误;
B.应为连接两点的线段的长度叫做两点的距离,故本小题错误;
C.射线与直线不能比较长短,故本小题错误;
D.因为A、B、C三点在同一直线上,且AB=BC,所以点B是线段AC的中点,故本小题正确;
故选:D.
4.悉尼、伦敦与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市 悉尼 伦敦
时差/时 +2 ﹣8
当北京12月12日23时,悉尼、伦敦的时间分别是( )
A.12月13日1时;12月12日15时
B.12月13日1时;12月11日15时
C.12月12日21时;12月12日15时
D.12月12日21时;12月13日7时
【分析】由统计表得出:悉尼时间比北京时间早2小时,也就是12月13日1时.伦敦比北京时间要晚8个小时,也就是12月12日15时.
解:悉尼的时间是:12月12日23时+2小时=12月13日1时,
伦敦时间是:12月12日23时﹣8小时=12月12日15时.
故选:A.
5.如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开,外表面朝上,展开图可能是( )
A. B.
C. D.
【分析】根据正方体的表面展开图进行分析解答即可.
解:根据正方体的表面展开图可得,展开图可能是:
或
故选:A.
6.下列运算正确的是( )
A.2a2+3a2=5a4 B.(﹣a3b)2=a6b2
C.2a a2=2a2 D.﹣2a(a﹣b)=﹣2a2﹣2ab
【分析】直接利用合并同类项法则以及积的乘方运算法则、单项式乘单项式、单项式乘多项式运算法则,分别判断得出答案.
解:A.2a2+3a2=5a2,故此选项不合题意;
B.(﹣a3b)2=a6b2,故此选项符合题意;
C.2a a2=2a3,故此选项不合题意;
D.﹣2a(a﹣b)=﹣2a2+2ab,故此选项不合题意;
故选:B.
7.关于x的方程2(x﹣1)﹣a=0的根是3,则a的值为( )
A.4 B.﹣4 C.5 D.﹣5
【分析】虽然是关于x的方程,但是含有两个未知数,其实质是知道一个未知数的值求另一个未知数的值.
解:把x=3代入2(x﹣1)﹣a=0中:
得:2(3﹣1)﹣a=0
解得:a=4
故选:A.
8.下列调查中,适合采用普查方式的是( )
A.了解七年级学生对“社会主义核心价值观”的知晓率
B.质监部门对各厂家生产的电池的使用寿命进行调查
C.对我国首艘国产航母山东舰各零部件质量情况的调查
D.调查我市市民知晓“礼让行人”交通新规情况
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
解:A.了解七年级学生对“社会主义核心价值观”的知晓率,适合采用抽样调查方式,故本选项不符合题意;
B.质监部门对各厂家生产的电池的使用寿命进行调查,适合采用抽样调查方式,故本选项不符合题意;
C.对我国首艘国产航母山东舰各零部件质量情况的调查,适合采用全面调查方式,故本选项符合题意;
D.调查我市市民知晓“礼让行人”交通新规情况,适合采用抽样调查方式,故本选项不符合题意;
故选:C.
9.对于代数式(ab2﹣4a﹣1)+(﹣3ab+b2a﹣3)﹣(2ab2﹣3ab)的值的描述,下列说法正确的是( )
A.与a,b的取值都有关
B.与a的取值有关,而与b的取值无关
C.与b取值有关,而与a的取值无关
D.与a,b的取值均无关
【分析】原式去括号合并得到最简结果,判断即可.
解:(ab2﹣4a﹣1)+(﹣3ab+b2a﹣3)﹣(2ab2﹣3ab)
=ab2﹣4a﹣1﹣3ab+b2a﹣3﹣2ab2+3ab
=﹣4a﹣4,
则代数式的值与与a的取值有关,而与b的取值无关.
故选:B.
10.如图所示的一个长方形,它被分割成6个正方形A,B,C,D,E,F,其中A,B两个正方形面积相同,如果中间最小的正方形F边长为1,则这个长方形的面积是( )
A.123 B.142 C.143 D.144
【分析】设正方形C的边长为x,则正方形E的边长为(x+1),正方形B的边长为(2x﹣1),正方形F的边长为(x+2),由长方形的对边相等,即可得出关于x的一元一次方程,解之即可得出x的值,再利用长方形的面积公式即可求出结论.
解:设正方形C的边长为x,则正方形E的边长为(x+1),正方形B的边长为(2x﹣1),正方形F的边长为(x+2),
依题意,得:x+(2x﹣1)=(x+1)+(x+2),
解得:x=4,
∴S=[x+x+(x+1)] [(x+1)+(x+2)]=13×11=143.
故选:C.
11.甲乙两桶共有48千克水,如果甲桶给乙桶加乙桶水的一倍,然后乙桶又给甲桶加甲桶剩水的一倍,那么两桶水的质量相等,问原来甲、乙两桶内各有多少千克水?若设原来乙桶内水的质量为x千克,则可列方程为( )
A.2(48﹣x﹣x)=(x+x)﹣(48﹣x﹣x)
B.2[x﹣(48﹣x)]=2(48﹣x)﹣[x﹣(48﹣x)]
C.2(48﹣x﹣x)=(x+48﹣x)﹣(48﹣x﹣x)
D.(48﹣x﹣x)+(x+x)=(x+48﹣x)﹣(48﹣x﹣x)
【分析】设甲桶内原有水xkg,则乙桶内原有水(48﹣x)kg,若乙桶的水增加1倍,则甲桶给乙桶加(48﹣x)kg水,此时甲桶有x﹣(48﹣x),然后用同样的方法解决乙桶给甲桶加水,为甲桶剩余的水的一倍的问题,最后利用两桶内水的质量相等列方程2(2x﹣48)=2(48﹣x)﹣(2x﹣48),再解方程求出x后计算48﹣x即可.
解:设甲桶内原有水xkg,则乙桶内原有水(48﹣x)kg,
根据题意得2(2x﹣48)=2(48﹣x)﹣(2x﹣48),
故选:B.
12.想象有一条很长的绳子可以绕地球赤道一圈,且绳子与地球之间的间隙是p厘米,设地球半径为d千米,则绳子的长度比地球赤道的长度长( )
A.[2π(d+p)﹣2πd]厘米 B.(2πd﹣2πp)厘米
C.2πd厘米 D.2πp厘米
【分析】由题知绳子的长度是2π(d×105+p)厘米,地球赤道的长度为2πd×105厘米,故绳子的长度比地球赤道的长度长2π(d×105+p)﹣2πd×105=2πp厘米.
解:由题知,d千米=d×105厘米,
∴绳子的长度是2π(d×105+p) 厘米,
地球赤道的长度为2πd×105厘米,
故绳子的长度比地球赤道的长度长2π(d×105+p)﹣2πd×105=2πp厘米,
故选:D.
二、填空题(本题共6个小题;每小题3分,共18分)
13.已知|a﹣4|+(2b+1)2=0,则a﹣b= .
【分析】直接利用绝对值和偶次方非负数的性质得出a,b的值,进而得出答案.
解:∵|a﹣4|+(2b+1)2=0,而|a﹣4|≥0,(2b+1)2≥0,
∴a﹣4=0,2b+1=0,
解得a=4,b=,
∴=.
故答案为:.
14.已知a﹣2b=﹣,则代数式2a﹣4b+1的值是 ﹣ .
【分析】将代数式2a﹣4b+1变形为2(a﹣2b)+1,将a﹣2b=﹣带入即可.
解:∵a﹣2b=﹣,
∴2a﹣4b+1=2(a﹣2b)+1=2×+1=﹣,
故答案为:﹣.
15.中国互联网络信息中心数据显示,截至2019年6月,我国网络购物用户规模达6.39亿,较2018年底增长2871万,占网民整体的74.8%,2871万用科学记数法表示为 2.871×107 .
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,且n比原来的整数位数少1,据此判断即可.
解:2871万=28710000=2.871×107.
故答案为:2.871×107.
16.如图,将一根绳子对折以后用线段AB表示,现从点C处将绳子剪断,剪断后的各段绳子中最长的一段为60cm,且AC=BC,则这条绳子的原长为 80cm或240cm .
【分析】根据绳子对折以后用线段AB表示,可得绳长是AB的2倍,分类讨论,CB的2倍最长,可得CB,AC的2倍最长,可得AC的长,再根据线段间的比例关系,可得答案.
解:当CB的2倍最长时,得
CB=30cm,
AC=CB=10cm,
AB=AC+CB=40cm,
这条绳子的原长为2AB=80cm;
当AC的2倍最长时,得
AC=30cm,AC=CB,
CB=3AC=90cm,
AB=AC+CB=120cm,
这条绳子的原长为2AB=240cm.
故答案为:80cm或240cm.
17.为了加强公民节水意识,合理利用水资源,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定立方米及以下的部分和超出部分标准不同.下表反映的是小亮家1﹣4月份用水量与应交水费情况:
月份 1 2 3 4
用水量(m3) 6 8 10 12
费用(元) 9 12 18 24
小亮家12月份用水xm3(12月份用水量超过规定用水量),应交水费y元,则y关于x的函数关系式是 y=3x﹣12(x>8) .
【分析】根据表格判断出1,2月份未超过用水量,3,4月份超过用水量,然后通过待定系数法求解.
解:由题得1﹣2月用水量增加2m3,水费增加3元,2﹣3月,3﹣4月水量增加2m3,水费增加6元,
∴1,2月y与x的关系式为设y=kx+b,
把x=6,y=9和x=8,y=12代入y=kx+b得,
解得,
∴y=x(0≤x≤8).
设3,4月份y与x的关系为y=mx+n,
把x=10,y=18和x=12,y=24代入y=mx+n得,
解得,
∴y=3x﹣12(x>8).
∵12月用水量超过规定用水量,
故答案为:y=3x﹣12(x>8).
18.有一系列方程,第1个方程是﹣(x﹣2)=1,解为x=;第2个方程是﹣(x﹣3)=1,解为x=;第3个方程是﹣(x﹣4)=1,解为x=,…,根据规律第7个方程﹣(x﹣8)=1,解为 x= .
【分析】根据已知三个方程的特点及解的特点得到一般性规律,即可确定出第7个方程的解.
解:根据题意得到第n个方程为,解为:x=(n为正整数),
∴第7个方程﹣(x﹣8)=1,解为=.
故答案为:x=.
三、解答题(本题共7个大题,共66分,解答应写出文字说明或推演步骤)
19.计算:
(1)×(﹣25)﹣(﹣25)×+(﹣25)÷8;
(2)﹣12019﹣0.54×25+32×(﹣)5.
【分析】(1)将除法转化为乘法,再逆用乘法分配律进一步计算即可;
(2)先计算乘方,再进一步计算即可.
解:(1)原式=×(﹣25)﹣(﹣25)×+(﹣25)×
=(﹣25)×(++)
=(﹣25)×
=﹣;
(2)原式=﹣1﹣(0.5×2)4×2+32×(﹣)
=﹣1﹣2﹣1
=﹣4.
20.解方程:
(1)2(3x﹣4)﹣3(4+3x)=4x﹣7(5﹣2x);
(2)x﹣=.
【分析】(1)方程去括号,移项合并,把未知数系数化为1,求出解即可;
(2)方程去分母,去括号,移项合并,把未知数系数化为1,求出解即可.
解:(1)2(3x﹣4)﹣3(4+3x)=4x﹣7(5﹣2x),
去括号,得6x﹣8﹣12﹣9x=4x﹣35+14x,
移项,得6x﹣9x﹣4x﹣14x=8+12﹣35,
合并同类项,得﹣21x=﹣15,
系数化为1,得;
(2)x﹣=,
去分母,得12x﹣4(1﹣4x)=3(11x+7),
去括号,得12x﹣4+16x=33x+21,
移项,得12x+16x﹣33x=21+4,
合并同类项,得﹣5x=25,
系数化为1,得x=﹣5.
21.(1)化简求值:已知:A=a2﹣3ab﹣2b2,B=a2﹣6ab+2b2,且a=,|b|=1,求3A﹣2B的值;
(2)已知关于字母x,y的多项式x2﹣3kxy﹣5y2﹣(﹣2xy﹣7)化简后不含xy项,求k的值.
【分析】(1)根据整式的加减运算法则进行化简,然后将a与b的值代入原式即可求出答案.
(2)根据整式的加减运算法则进行化简,然后令含xy的项的系数之和为0即可求出k的值.
解:(1)3A﹣2B
=3(a2﹣3ab﹣2b2)﹣2(a2﹣6ab+2b2)
=3a2﹣9ab﹣6b2﹣2a2+12ab﹣4b2
=a2+3ab﹣10b2,
由题意可知:a=,b=±1,
当a=,b=1时,
原式=+3××1﹣10×1
=+﹣10
=.
当a=,b=﹣1时,
原式=﹣3××1﹣10×1
=﹣﹣10
=.
(2)原式=x2﹣3kxy﹣5y2+2xy+7
=x2+(2﹣3k)xy﹣5y2+7,
令2﹣3k=0,
∴k=.
22.“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 600 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
【分析】(1)由B的人数除以占的百分比求出调查的人数即可;
(2)求出C的人数与百分比,A的百分比,补全两个图形即可;
(3)由A的百分比乘以360即可得到结果;
(4)由D的百分比乘以8000即可得到结果.
解:(1)本次参加抽样调查的居民的人数是:60÷10%=600(人);
故答案为:600;
(2)由题意得:C的人数为600﹣(180+60+240)=600﹣480=120(人),C的百分比为120÷600×100%=20%;A的百分比为180÷600×100%=30%;
(3)根据题意得:360°×30%=108°,
图②中表示“A”的圆心角的度数108°;
(4)8000×40%=3200(人),
即爱吃D汤圆的人数约为3200人.
23.火柴拼图是一种道具简单、开启思维、挖掘智力、陶冶情趣的数字游戏.这种游戏形式万千,可简可繁.七年级的同学们学了“用字母表示数”和“列代数式”的内容后,数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动.他们按照下图所示的方法拼图,探究不同图形中共拼出的三角形个数,正方形的个数及所用火柴棒的根数与所拼图之间的关系,请你参与进去进行数学探究活动.
(1)观察发现:观察下图中正方形的个数及所用火柴棒根数,并填写下表中的空格:
第1个 第2个 第3个 第4个 …
拼成三角形个数 1 2 3 4 …
拼成的正方形个数 3 5 7 9 …
所用火柴棒总根数 12 20 28 36 …
(2)拓展探究:按如图所示的方法拼成的第n个图中,三角形和正方形的个数各有多少?所用的火柴棒总根数是多少?(用含n的代数式表示)
(3)迁移应用:按这种拼图方法拼出的第10个图中三角形和正方形各有多少个?共需要火柴棒多少根?
【分析】(1)观察图形的变化即可完成填空;
(2)结合(1)即可得第n个图形的三角形和正方形的个数以及火柴棒个数;
(3)把n=10代入可得答案.
解:(1)第3个图形中,拼成三角形的个数是3个,拼成正方形的个数是7个,所用火柴棒总根数是28根;
第4个图形中,拼成三角形的个数是4个,拼成正方形的个数是9个,所用火柴棒总根数是36根;
故答案为:3,7,28;4,9,36.
(2)由(1)可得,
第n个图形中,拼成三角形的个数是n个,拼成正方形的个数是(2n+1)个,所用火柴棒总根数是(8n+4)根.
(3)当n=10时,拼成三角形的个数是10个,
拼成正方形的个数是2×10+1=21(个),
所用火柴棒总根数是8×10+4=84(根).
24.阳光中学七年级学生从学校出发去郊游,带队的老师和学生们以4km/h的速度步行前进,20min后,小明骑自行车前去追赶.已知小明骑自行车速度比队伍步行速度多8km/h,那么小明要用多少时间才能追上队伍?此时队伍已行走了多远?
【分析】设小明要用xh才能追上队伍,则队伍行走的时间是(x+)h.根据他们所行驶的路程相等列出方程并求得x的值;然后根据路程=时间×速度计算队伍行走的路程.
解:设小明要用xh才能追上队伍,则队伍行走的时间是(x+)h,
根据题意,得4(x+)=(4+8)x,
解得x=.
所以4(x+)=4(+)=2.
答:小明要用小时才能追上队伍,此时队伍已行走了2km.
25.某商场在“十一”国庆节期间搞促销活动,活动方案如下:
一次性购物总额 优惠方案
不超过500元 不给予优惠
超过500元,但不超过800元 8折优惠
超过800元 其中800元给予8折优惠,超过800元的部分给予6折优惠
小莹的妈妈在促销期间,两次购物分别支付了360元和880元.
(1)小莹的妈妈两次购买的商品如果不打折,应支付多少钱?在此活动中,她节省了多少钱?
(2)若两次购物一起支付,则小莹的妈妈只需付款多少元?
【分析】(1)由500×0.8=400,360<400,可知第一次购买的商品如果不打折,应支付360元,而超过500元,但不超过800元的8折优惠,超过800元的,800元给予8折优惠,超过800元的部分给予6折优惠,可知第二次购买的商品如果不打折,应支付1200元,即得小莹的妈妈两次购买的商品如果不打折,应支付1560元,她节省了320元;
(2)根据800元给予8折优惠,超过800元的部分给予6折优惠,即可得两次购物一起支付,小莹的妈妈付款为1096元.
解:(1)∵500×0.8=400,360<400,
∴支付了360元,商品没打折,即第一次购买的商品如果不打折,应支付360元,
∵800×0.8=640,880﹣640=240,240÷0.6=400,800+400=1200,
∴第二次购买的商品如果不打折,应支付1200元,
∴小莹的妈妈两次购买的商品如果不打折,应支付1560元,
而1560﹣(360+880)=320,
∴在此活动中,她节省了320元;
(2)800×0.8+(1560﹣800)×0.6=1096(元),
∴若两次购物一起支付,则小莹的妈妈只需付款1096元.
同课章节目录
