北师大版七年级数学上册 1.2 展开与折叠-蚂蚁怎样走最近(课件)(共21张PPT)
文档属性
| 名称 | 北师大版七年级数学上册 1.2 展开与折叠-蚂蚁怎样走最近(课件)(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
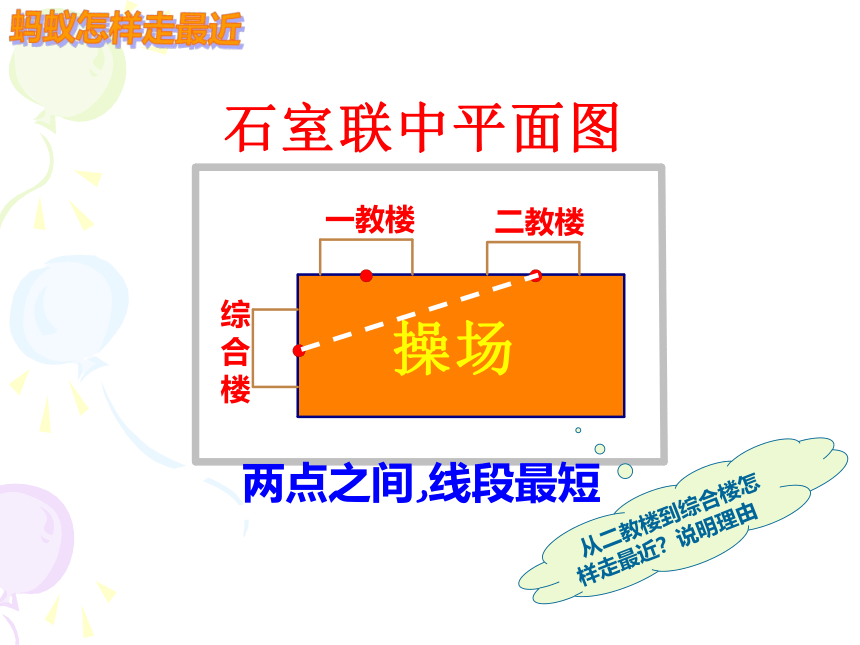
从二教楼到综合楼怎样走最近?说明理由
两点之间,线段最短
B
A
蚂蚁怎么走最近
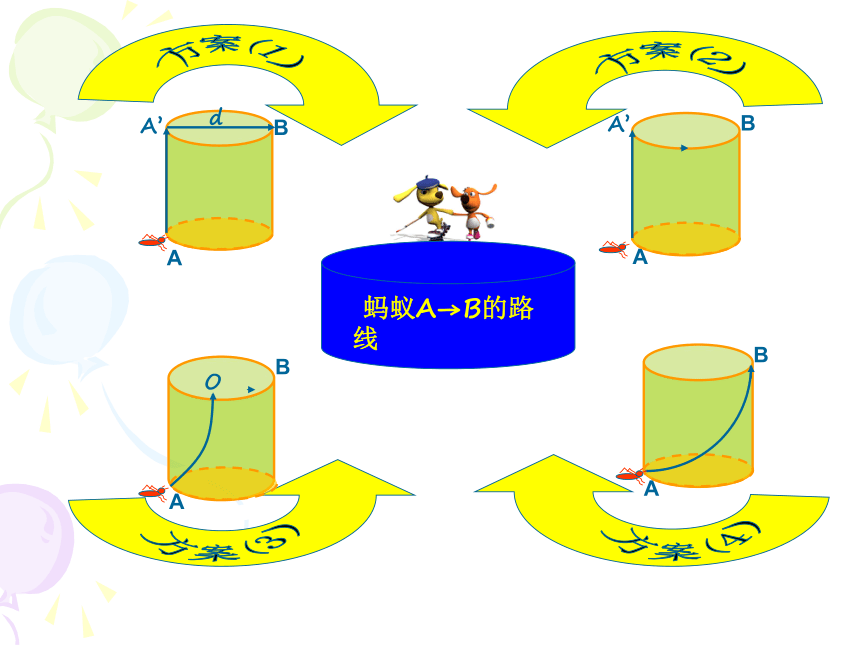
在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A 处爬向B处,你们想一想,蚂蚁怎么走最近?
B
A
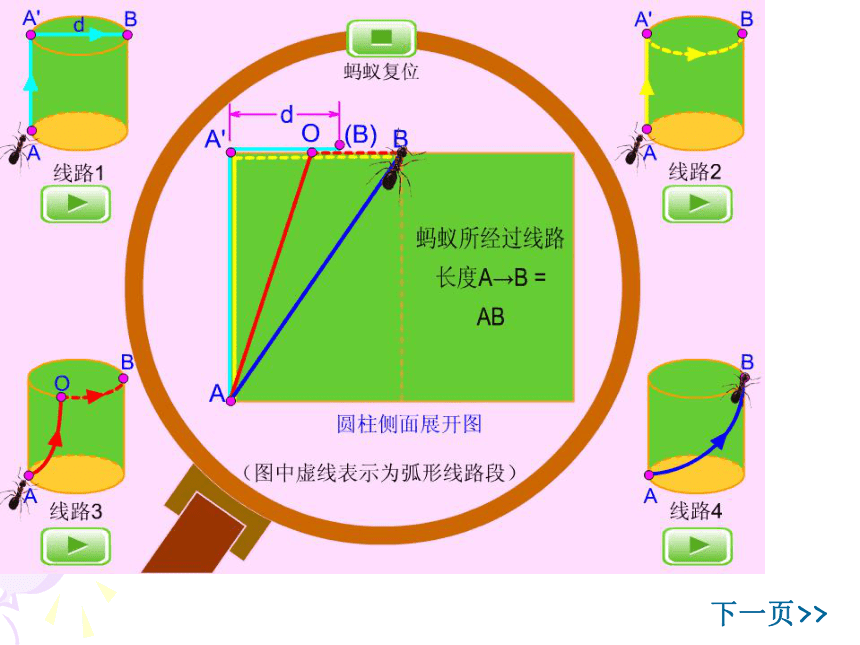
以小组为单位,研究蚂蚁爬行的最短路线
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
下一页>>
A
B
A’
B
A
A’
r
O
h
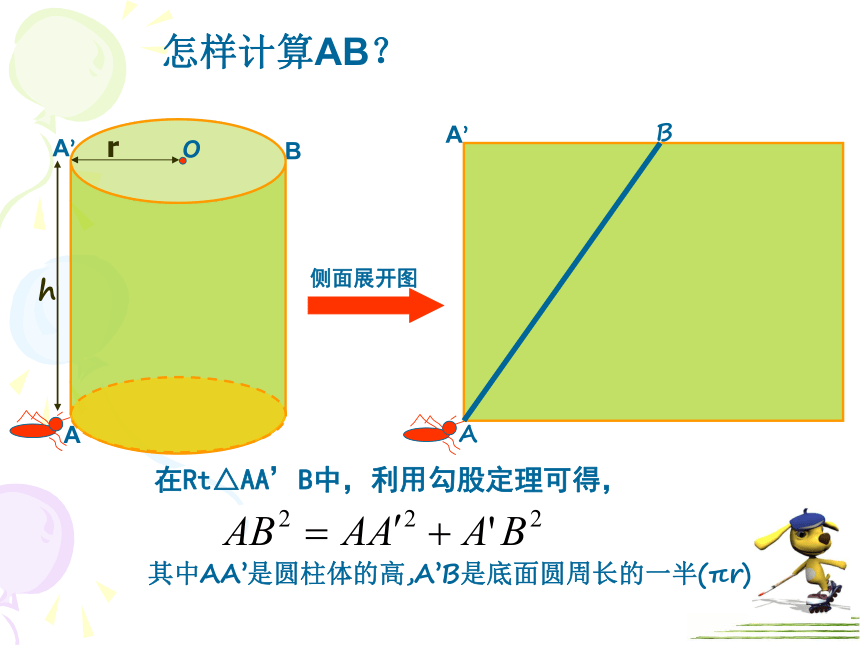
怎样计算AB?
在Rt△AA’B中,利用勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
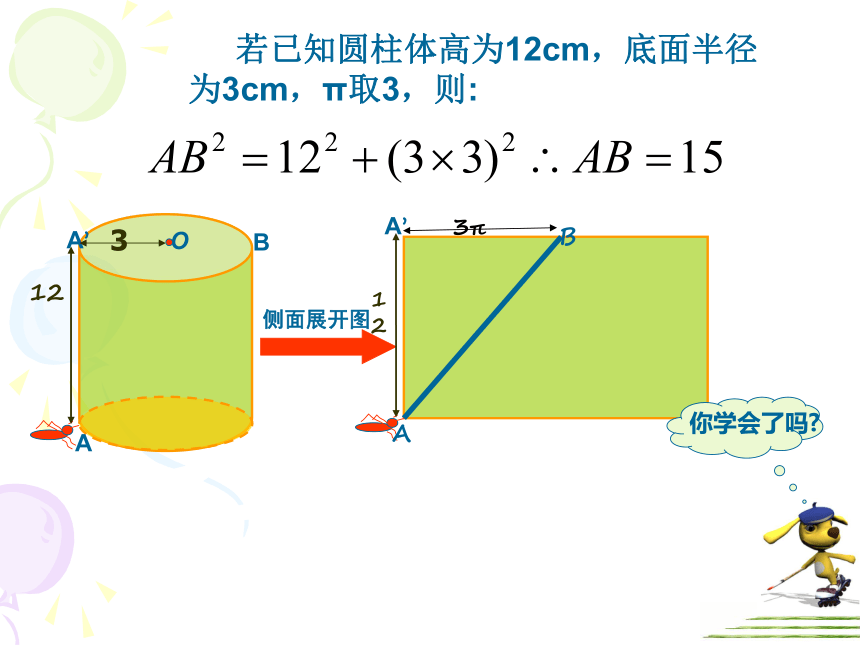
若已知圆柱体高为12cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
12
侧面展开图
12
3π
A
A’
B
你学会了吗
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
∴AD和AB垂直
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
小试牛刀
练习1
练习2
练习3
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(千米)
AC=1×5=5(千米)
在Rt△ABC中
∴BC=13(千米)
即甲乙两人相距13千米
小试牛刀
练习1
练习2
练习3
2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离。
小试牛刀
练习1
练习2
练习3
3.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?
你能画出示意图吗
解:设伸入油桶中的长度为x米,则最长时:
最短时:
∴最长是2.5+0.5=3(米)
答:这根铁棒的长应在2-3米之间
∴最短是1.5+0.5=2(米)
举一反三
练习1
练习2
1.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?
B
食物
A
举一反三
练习1
练习2
1.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?
B
A
B
两条线路,看明白了吗
举一反三
练习1
练习2
中国古代人民的聪明才智真是令人赞叹 !
2.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
举一反三
练习1
练习2
解:设水池的水深AC为x尺,则这根芦苇长为
AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1,
2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺。
课后作业
2*.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗 请你与同伴交流设计方案
1.课本习题1.5第1,2,3题。
从二教楼到综合楼怎样走最近?说明理由
两点之间,线段最短
B
A
蚂蚁怎么走最近
在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A 处爬向B处,你们想一想,蚂蚁怎么走最近?
B
A
以小组为单位,研究蚂蚁爬行的最短路线
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
下一页>>
A
B
A’
B
A
A’
r
O
h
怎样计算AB?
在Rt△AA’B中,利用勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
若已知圆柱体高为12cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
12
侧面展开图
12
3π
A
A’
B
你学会了吗
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
∴AD和AB垂直
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
小试牛刀
练习1
练习2
练习3
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(千米)
AC=1×5=5(千米)
在Rt△ABC中
∴BC=13(千米)
即甲乙两人相距13千米
小试牛刀
练习1
练习2
练习3
2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离。
小试牛刀
练习1
练习2
练习3
3.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?
你能画出示意图吗
解:设伸入油桶中的长度为x米,则最长时:
最短时:
∴最长是2.5+0.5=3(米)
答:这根铁棒的长应在2-3米之间
∴最短是1.5+0.5=2(米)
举一反三
练习1
练习2
1.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?
B
食物
A
举一反三
练习1
练习2
1.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?
B
A
B
两条线路,看明白了吗
举一反三
练习1
练习2
中国古代人民的聪明才智真是令人赞叹 !
2.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
举一反三
练习1
练习2
解:设水池的水深AC为x尺,则这根芦苇长为
AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1,
2 x=24,
∴ x=12, x+1=13
答:水池的水深12尺,这根芦苇长13尺。
课后作业
2*.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗 请你与同伴交流设计方案
1.课本习题1.5第1,2,3题。
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
