11.1 与三角形有关的线段 专项复习 2021-2022学年人教版版八年级上册数学(word版含答案)
文档属性
| 名称 | 11.1 与三角形有关的线段 专项复习 2021-2022学年人教版版八年级上册数学(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 132.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 09:43:38 | ||
图片预览




文档简介
人教版八年级上册数学期中常考题
《与三角形有关的线段》专项复习
一.选择题(共5小题)
1.(2021春 信都区期末)如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
2.(2020秋 无棣县期末)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
3.(2021春 姑苏区期中)如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
4.(2021春 宽城县期末)下列长度的三条线段能组成三角形的是( )
A.5cm,2cm,4cm B.5cm,2cm,2cm
C.5cm,2cm,3cm D.5cm,12cm,6cm
5.(2021春 道外区期末)如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
二.填空题(共5小题)
6.(2020春 宝安区期中)一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 三角形.
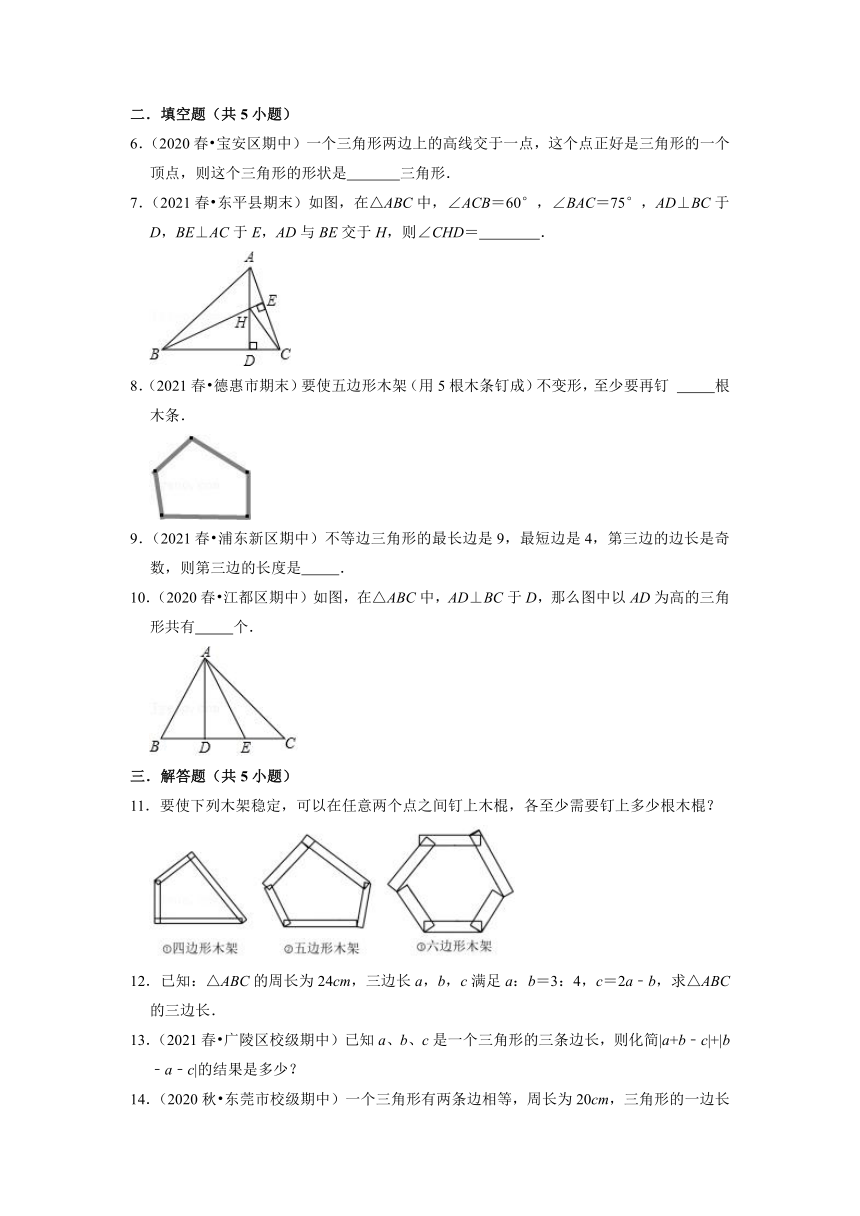
7.(2021春 东平县期末)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
8.(2021春 德惠市期末)要使五边形木架(用5根木条钉成)不变形,至少要再钉 根木条.
9.(2021春 浦东新区期中)不等边三角形的最长边是9,最短边是4,第三边的边长是奇数,则第三边的长度是 .
10.(2020春 江都区期中)如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有 个.
三.解答题(共5小题)
11.要使下列木架稳定,可以在任意两个点之间钉上木棍,各至少需要钉上多少根木棍?
12.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
13.(2021春 广陵区校级期中)已知a、b、c是一个三角形的三条边长,则化简|a+b﹣c|+|b﹣a﹣c|的结果是多少?
14.(2020秋 东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
15.(2021春 汝阳县期末)如图,在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
参考答案
一.选择题(共5小题)
1.(2021春 信都区期末)如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
【考点】三角形的角平分线、中线和高.
【分析】根据三角形的角平分线的定义,三角形的中线的定义可知.
【解答】解:AD是三角形ABC的角平分线,
则是∠BAC的角平分线,
所以AO是△ABE的角平分线,故①正确;
BE是三角形ABC的中线,
则E是AC是中点,而O不一定是AD的中点,故②错误.
故选:C.
【点评】考查了三角形的角平分线和中线的概念.
2.(2020秋 无棣县期末)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
【考点】三角形.
【专题】三角形.
【分析】根据三角形的分类可直接得到答案.
【解答】解:三角形根据边分类 ,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
【点评】此题主要考查了三角形的分类,关键是掌握分类方法.按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
3.(2021春 姑苏区期中)如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
【考点】三角形的稳定性.
【专题】三角形;应用意识.
【分析】根据三角形的稳定性解答即可.
【解答】解:如图,根据三角形的稳定性可知,要使五边形木架不变形,至少要再钉上2根木条,
故选:B.
【点评】本题考查的是三角形的稳定性,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
4.(2021春 宽城县期末)下列长度的三条线段能组成三角形的是( )
A.5cm,2cm,4cm B.5cm,2cm,2cm
C.5cm,2cm,3cm D.5cm,12cm,6cm
【考点】三角形三边关系.
【专题】三角形;运算能力.
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:A、2+4>5,能构成三角形,符合题意;
B、2+2<5,不能构成三角形,不符合题意;
C、2+3=5,不能构成三角形,不符合题意;
D、5+6<12,不能构成三角形,不符合题意.
故选:A.
【点评】此题主要考查了三角形三边关系,根据第三边的范围是:大于已知的两边的差,而小于两边的和是解决问题的关键.
5.(2021春 道外区期末)如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
【考点】三角形.
【专题】三角形.
【分析】根据三角形的定义,找出图中所有的三角形,数出其个数即可得出结论.
【解答】解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
【点评】本题考查了三角形,牢记三角形的定义是解题的关键.
二.填空题(共5小题)
6.(2020春 宝安区期中)一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 直角 三角形.
【考点】三角形.
【专题】三角形;空间观念.
【分析】根据三种三角形的高的特点解答.
【解答】解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
【点评】本题考查了三角形,关键是掌握直角三角形的特点.
7.(2021春 东平县期末)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= 45° .
【考点】三角形的角平分线、中线和高.
【专题】常规题型.
【分析】延长CH交AB于点F,锐角三角形三条高交于一点,所以CF⊥AB,再根据三角形内角和定理得出答案.
【解答】解:延长CH交AB于点F,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,
∴∠ACF=15°,
∵∠ACB=60°,
∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
故答案为∠CHD=45°.
【点评】考查三角形中,三条边的高交于一点,且内角和为180°.
8.(2021春 德惠市期末)要使五边形木架(用5根木条钉成)不变形,至少要再钉 2 根木条.
【考点】三角形的稳定性.
【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.
【解答】解:再钉上两根木条,就可以使五边形分成三个三角形.故至少要再钉两根木条.
【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
9.(2021春 浦东新区期中)不等边三角形的最长边是9,最短边是4,第三边的边长是奇数,则第三边的长度是 7 .
【考点】三角形三边关系.
【专题】三角形;几何直观.
【分析】根据三角形的三边关系即可求得第三边的范围,从而由不等边三角形和奇数的定义确定第三边的长度.
【解答】解:设第三边长是c,则9﹣4<c<9+4,
即5<c<13,
又∵第三边的长是奇数,不等边三角形的最长边为9,最短边为4,
∴c=7.
故答案为:7.
【点评】本题考查了三角形的三边关系,已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.
10.(2020春 江都区期中)如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有 6 个.
【考点】三角形.
【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.
【解答】解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6
【点评】此题主要考查了三角形的高,三角形的高可以在三角形外,也可以在三角形内,所以确定三角形的高比较灵活.
三.解答题(共5小题)
11.要使下列木架稳定,可以在任意两个点之间钉上木棍,各至少需要钉上多少根木棍?
【考点】三角形的稳定性.
【专题】常规题型.
【分析】根据三角形具有稳定性可得答案.
【解答】解:图①四边形木架至少需要钉上1根木棍;
图②五边形木架至少需要钉上2根木棍;
图③六边形木架至少需要钉上3根木棍.
【点评】此题主要考查了三角形的稳定性,关键是掌握当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
12.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
【考点】三角形.
【专题】三角形;运算能力.
【分析】隐形方程为a+b+c=24,然后再联立两方程得出方程组,解出a、b、c即可.
【解答】解:由题意得,
解得:.
故△ABC的三边长为8cm,cm,cm.
【点评】本题考查了三角形,三元一次方程组的应用,解答本题的关键是得出隐形方程a+b+c=24,难度一般.
13.(2021春 广陵区校级期中)已知a、b、c是一个三角形的三条边长,则化简|a+b﹣c|+|b﹣a﹣c|的结果是多少?
【考点】绝对值;三角形三边关系.
【专题】三角形;推理能力.
【分析】根据三角形三边关系得到a+b﹣c>0,b﹣a﹣c<0,再去绝对值,合并同类项即可求解.
【解答】解:∵a,b,c是一个三角形的三条边长,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|+|b﹣a﹣c|
=a+b﹣c+a+c﹣b
=2a.
【点评】此题考查了三角形三边关系,绝对值的性质,整式的加减,关键是得到a+b﹣c>0,b﹣a﹣c<0.
14.(2020秋 东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【考点】三角形.
【分析】题目给出等腰三角形有一条边长为6cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
15.(2021春 汝阳县期末)如图,在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
【考点】三角形的角平分线、中线和高.
【专题】几何图形.
【分析】根据三角形中线的定义求出AB、AC,再利用三角形的周长的定义列式计算即可得解.
【解答】解:∵CF、BE分别是AB、AC边上的中线,AE=2,AF=3,
∴AB=2AF=2×3=6,
AC=2AE=2×2=4,
∵△ABC的周长为15,
∴BC=15﹣6﹣4=5.
【点评】本题考查了三角形的角平分线、中线和高,熟记概念并准确识图是解题的关键.
《与三角形有关的线段》专项复习
一.选择题(共5小题)
1.(2021春 信都区期末)如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
2.(2020秋 无棣县期末)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
3.(2021春 姑苏区期中)如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
4.(2021春 宽城县期末)下列长度的三条线段能组成三角形的是( )
A.5cm,2cm,4cm B.5cm,2cm,2cm
C.5cm,2cm,3cm D.5cm,12cm,6cm
5.(2021春 道外区期末)如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
二.填空题(共5小题)
6.(2020春 宝安区期中)一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 三角形.
7.(2021春 东平县期末)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
8.(2021春 德惠市期末)要使五边形木架(用5根木条钉成)不变形,至少要再钉 根木条.
9.(2021春 浦东新区期中)不等边三角形的最长边是9,最短边是4,第三边的边长是奇数,则第三边的长度是 .
10.(2020春 江都区期中)如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有 个.
三.解答题(共5小题)
11.要使下列木架稳定,可以在任意两个点之间钉上木棍,各至少需要钉上多少根木棍?
12.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
13.(2021春 广陵区校级期中)已知a、b、c是一个三角形的三条边长,则化简|a+b﹣c|+|b﹣a﹣c|的结果是多少?
14.(2020秋 东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
15.(2021春 汝阳县期末)如图,在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
参考答案
一.选择题(共5小题)
1.(2021春 信都区期末)如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
【考点】三角形的角平分线、中线和高.
【分析】根据三角形的角平分线的定义,三角形的中线的定义可知.
【解答】解:AD是三角形ABC的角平分线,
则是∠BAC的角平分线,
所以AO是△ABE的角平分线,故①正确;
BE是三角形ABC的中线,
则E是AC是中点,而O不一定是AD的中点,故②错误.
故选:C.
【点评】考查了三角形的角平分线和中线的概念.
2.(2020秋 无棣县期末)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
【考点】三角形.
【专题】三角形.
【分析】根据三角形的分类可直接得到答案.
【解答】解:三角形根据边分类 ,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
【点评】此题主要考查了三角形的分类,关键是掌握分类方法.按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
3.(2021春 姑苏区期中)如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
【考点】三角形的稳定性.
【专题】三角形;应用意识.
【分析】根据三角形的稳定性解答即可.
【解答】解:如图,根据三角形的稳定性可知,要使五边形木架不变形,至少要再钉上2根木条,
故选:B.
【点评】本题考查的是三角形的稳定性,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
4.(2021春 宽城县期末)下列长度的三条线段能组成三角形的是( )
A.5cm,2cm,4cm B.5cm,2cm,2cm
C.5cm,2cm,3cm D.5cm,12cm,6cm
【考点】三角形三边关系.
【专题】三角形;运算能力.
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:A、2+4>5,能构成三角形,符合题意;
B、2+2<5,不能构成三角形,不符合题意;
C、2+3=5,不能构成三角形,不符合题意;
D、5+6<12,不能构成三角形,不符合题意.
故选:A.
【点评】此题主要考查了三角形三边关系,根据第三边的范围是:大于已知的两边的差,而小于两边的和是解决问题的关键.
5.(2021春 道外区期末)如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
【考点】三角形.
【专题】三角形.
【分析】根据三角形的定义,找出图中所有的三角形,数出其个数即可得出结论.
【解答】解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
【点评】本题考查了三角形,牢记三角形的定义是解题的关键.
二.填空题(共5小题)
6.(2020春 宝安区期中)一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 直角 三角形.
【考点】三角形.
【专题】三角形;空间观念.
【分析】根据三种三角形的高的特点解答.
【解答】解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
【点评】本题考查了三角形,关键是掌握直角三角形的特点.
7.(2021春 东平县期末)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= 45° .
【考点】三角形的角平分线、中线和高.
【专题】常规题型.
【分析】延长CH交AB于点F,锐角三角形三条高交于一点,所以CF⊥AB,再根据三角形内角和定理得出答案.
【解答】解:延长CH交AB于点F,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,
∴∠ACF=15°,
∵∠ACB=60°,
∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
故答案为∠CHD=45°.
【点评】考查三角形中,三条边的高交于一点,且内角和为180°.
8.(2021春 德惠市期末)要使五边形木架(用5根木条钉成)不变形,至少要再钉 2 根木条.
【考点】三角形的稳定性.
【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.
【解答】解:再钉上两根木条,就可以使五边形分成三个三角形.故至少要再钉两根木条.
【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
9.(2021春 浦东新区期中)不等边三角形的最长边是9,最短边是4,第三边的边长是奇数,则第三边的长度是 7 .
【考点】三角形三边关系.
【专题】三角形;几何直观.
【分析】根据三角形的三边关系即可求得第三边的范围,从而由不等边三角形和奇数的定义确定第三边的长度.
【解答】解:设第三边长是c,则9﹣4<c<9+4,
即5<c<13,
又∵第三边的长是奇数,不等边三角形的最长边为9,最短边为4,
∴c=7.
故答案为:7.
【点评】本题考查了三角形的三边关系,已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.
10.(2020春 江都区期中)如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有 6 个.
【考点】三角形.
【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.
【解答】解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6
【点评】此题主要考查了三角形的高,三角形的高可以在三角形外,也可以在三角形内,所以确定三角形的高比较灵活.
三.解答题(共5小题)
11.要使下列木架稳定,可以在任意两个点之间钉上木棍,各至少需要钉上多少根木棍?
【考点】三角形的稳定性.
【专题】常规题型.
【分析】根据三角形具有稳定性可得答案.
【解答】解:图①四边形木架至少需要钉上1根木棍;
图②五边形木架至少需要钉上2根木棍;
图③六边形木架至少需要钉上3根木棍.
【点评】此题主要考查了三角形的稳定性,关键是掌握当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
12.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
【考点】三角形.
【专题】三角形;运算能力.
【分析】隐形方程为a+b+c=24,然后再联立两方程得出方程组,解出a、b、c即可.
【解答】解:由题意得,
解得:.
故△ABC的三边长为8cm,cm,cm.
【点评】本题考查了三角形,三元一次方程组的应用,解答本题的关键是得出隐形方程a+b+c=24,难度一般.
13.(2021春 广陵区校级期中)已知a、b、c是一个三角形的三条边长,则化简|a+b﹣c|+|b﹣a﹣c|的结果是多少?
【考点】绝对值;三角形三边关系.
【专题】三角形;推理能力.
【分析】根据三角形三边关系得到a+b﹣c>0,b﹣a﹣c<0,再去绝对值,合并同类项即可求解.
【解答】解:∵a,b,c是一个三角形的三条边长,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|+|b﹣a﹣c|
=a+b﹣c+a+c﹣b
=2a.
【点评】此题考查了三角形三边关系,绝对值的性质,整式的加减,关键是得到a+b﹣c>0,b﹣a﹣c<0.
14.(2020秋 东莞市校级期中)一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
【考点】三角形.
【分析】题目给出等腰三角形有一条边长为6cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
15.(2021春 汝阳县期末)如图,在△ABC中,CF、BE分别是AB、AC边上的中线,若AE=2,AF=3,且△ABC的周长为15,求BC的长.
【考点】三角形的角平分线、中线和高.
【专题】几何图形.
【分析】根据三角形中线的定义求出AB、AC,再利用三角形的周长的定义列式计算即可得解.
【解答】解:∵CF、BE分别是AB、AC边上的中线,AE=2,AF=3,
∴AB=2AF=2×3=6,
AC=2AE=2×2=4,
∵△ABC的周长为15,
∴BC=15﹣6﹣4=5.
【点评】本题考查了三角形的角平分线、中线和高,熟记概念并准确识图是解题的关键.
