第五章 利用平行四边形的性质和判定解题 专项训练 (含答案)
文档属性
| 名称 | 第五章 利用平行四边形的性质和判定解题 专项训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-07 20:14:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
利用平行四边形的性质和判定解题
类型一 证两条线段相等或求线段的长度
1.如图所示,在平行四边形ABCD中,AB=1,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,则EF的长是__________.
2.如图所示,在平行四边形ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.
类型二 求线段长的取值范围
3.如图所示,在△ABC中,AB=8,AC=6,AD为△ABC的中线,则AD的长的取值范围是_________.
类型三 解决面积问题
4.如图所示,四边形ABCD中,AD∥BC,E为DC的中点.求证:S△ABE=S四边形ABCD.
类型四 证两条线段互相平分
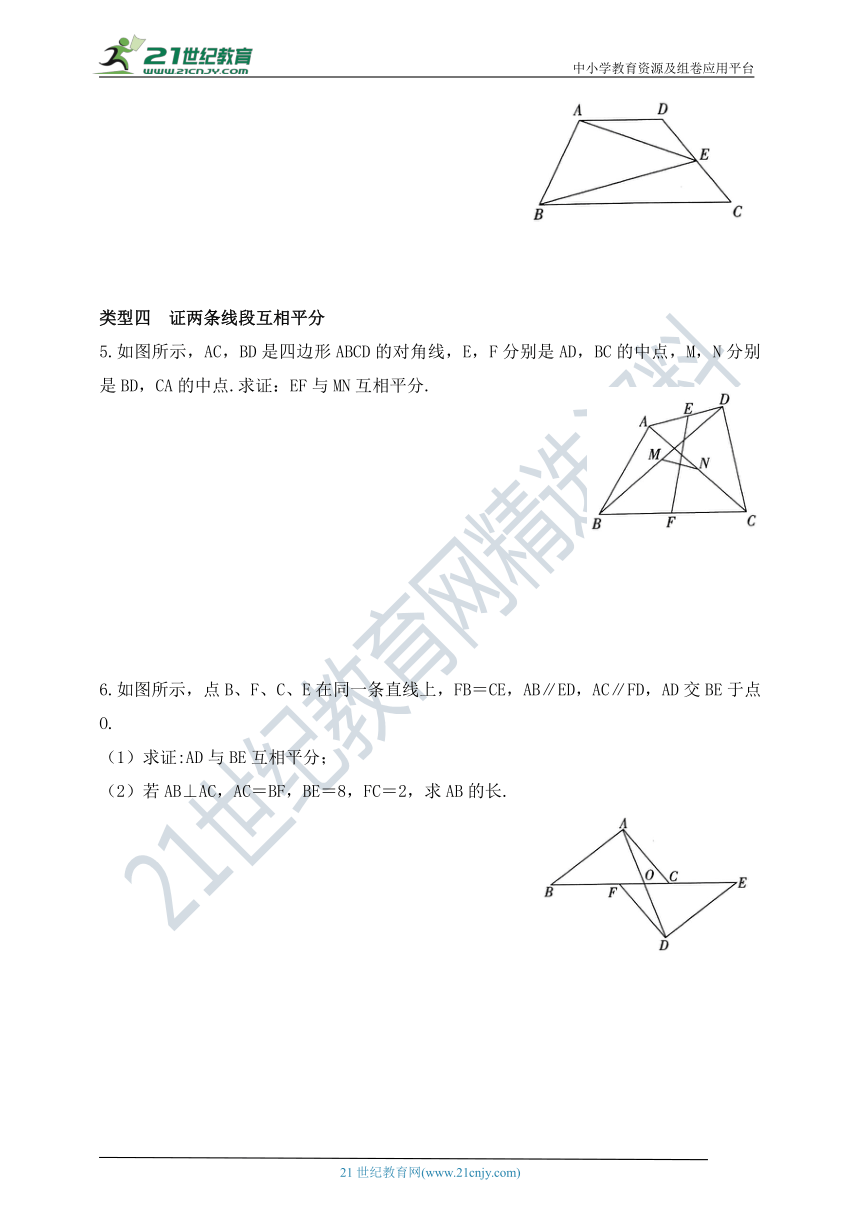
5.如图所示,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,CA的中点.求证:EF与MN互相平分.
6.如图所示,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.
(1)求证:AD与BE互相平分;
(2)若AB⊥AC,AC=BF,BE=8,FC=2,求AB的长.
类型五 证两条直线平行
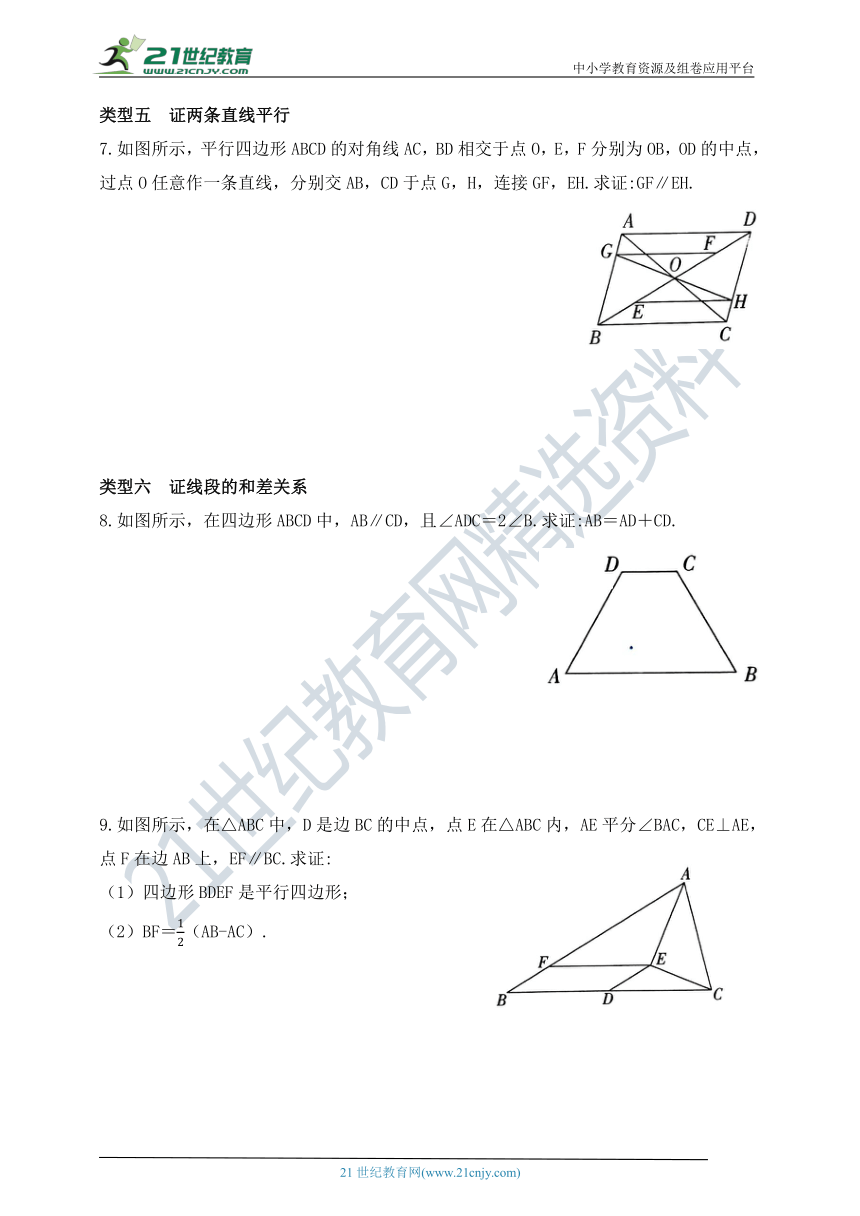
7.如图所示,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别为OB,OD的中点,过点O任意作一条直线,分别交AB,CD于点G,H,连接GF,EH.求证:GF∥EH.
类型六 证线段的和差关系
8.如图所示,在四边形ABCD中,AB∥CD,且∠ADC=2∠B.求证:AB=AD+CD.
9.如图所示,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.求证:
(1)四边形BDEF是平行四边形;
(2)BF=(AB-AC).
参考答案
2.证明 ∵在平行四边形ABCD中,BE∥CD,∴∠E=∠2,
∵CE平分∠BCD,∴∠1=∠2,∴∠1=∠E,∴BE=BC,
又∵BH⊥EC,∴CH=EH.
3. 1<AD<7
4.证明 如图,过点E作FH∥AB,交AD的延长线于点F,交BC于点H.
∵AD∥BC,FH∥AB,∴四边形ABHF为平行四边形.∴S△ABE=S平行四边形ABHF.
∵AD∥BC,∴∠F=∠1,∠2=∠C.
∵E为DC的中点,∴DE=CE,∴△DEF≌△CEH(AAS),∴DF=HC,
∴ S平行四边形ABHF=S四边形ABCD.∴S△ABE=S四边形ABCD.
5.证明 连接ME,MF,NE,NF,如图所示:
∵E,M分别是AD,BD的中点,∴ME是△ABD的中位线,∴ME∥AB,
同理,MF∥CD,EN∥CD,FN∥AB,∴ME∥FN,MF∥EN,
∴四边形EMFN是平行四边形,∴EF与MN互相平分.
6.解析 (1)证明:如图,连接BD,AE,
∵FB=CE,∴BC=EF,又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB=∠DFE.
在△ABC和△DEF中,∴△ABC≌△DEF(ASA),∴AB=DE,
又∵AB// DE,∴四边形ABDE是平行四边形,∴AD与BE互相平分.
(2)∵FB=CE,∴BE=2BF+FC,∴,
∴AC=BF=3, BC=BF+FC=3+2-5,
∵AB⊥AC,∴由勾股定理得AB==4.
7.证明 ∵四边形ABCD是平行四边形,∴AB∥CD, 0A=OC, OB=OD,∴∠BAC=∠DCA.
又∵OA=0C,∠AOG=∠COH,∴△AOG≌△COH(ASA),∴0G=OH.
∴E,F分别为OB,OD的中点,∴0E=0B,OF=0D,∴OE=OF.
如图,连接GE,HF.
∵OG=OH,OE=OF,∴四边形EHFG是平行四边形,∴CF∥EH.
8.证明 如图,过点D作DE//B,交AB于点E,∴∠B=∠1.
∵AB∥CD,DE∥BC,∴四边形DEBC是平行四边形.∴∠B=∠CDE,CD=BE.
又∵∠ADC=2∠B=∠ADE+∠CDE,∴∠ADE=∠B=∠1.
∴AD=AE,∴AB=AE+EB=AD+CD.
9.证明 (1)延长CE交AB于点G,如图所示:
∵AE平分∠BAC,∴∠GAE=∠CAE.
∵ AE⊥CE,∴∠AEG=∠AEC=90°,
在△AGE和△ACE中,∴△AGE≌△ACE(ASA),∴GE=EC.
又∵D是边BC的中点,∴DE为△CGB的中位线,∴DE∥AB.
又∵EF∥BC,∴四边形BDEF是平行四边形.
(2)由(1)可知四边形BDEF是平行四边形,∴BF=DE.
∵D、E分别是BC、GC的中点,∴BF=DE=BG
∵△AGE≌△ACE,∴AG=AC,∴BF=(AB-AG)=(AB-AC).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
利用平行四边形的性质和判定解题
类型一 证两条线段相等或求线段的长度
1.如图所示,在平行四边形ABCD中,AB=1,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,则EF的长是__________.
2.如图所示,在平行四边形ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.
类型二 求线段长的取值范围
3.如图所示,在△ABC中,AB=8,AC=6,AD为△ABC的中线,则AD的长的取值范围是_________.
类型三 解决面积问题
4.如图所示,四边形ABCD中,AD∥BC,E为DC的中点.求证:S△ABE=S四边形ABCD.
类型四 证两条线段互相平分
5.如图所示,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,CA的中点.求证:EF与MN互相平分.
6.如图所示,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.
(1)求证:AD与BE互相平分;
(2)若AB⊥AC,AC=BF,BE=8,FC=2,求AB的长.
类型五 证两条直线平行
7.如图所示,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别为OB,OD的中点,过点O任意作一条直线,分别交AB,CD于点G,H,连接GF,EH.求证:GF∥EH.
类型六 证线段的和差关系
8.如图所示,在四边形ABCD中,AB∥CD,且∠ADC=2∠B.求证:AB=AD+CD.
9.如图所示,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.求证:
(1)四边形BDEF是平行四边形;
(2)BF=(AB-AC).
参考答案
2.证明 ∵在平行四边形ABCD中,BE∥CD,∴∠E=∠2,
∵CE平分∠BCD,∴∠1=∠2,∴∠1=∠E,∴BE=BC,
又∵BH⊥EC,∴CH=EH.
3. 1<AD<7
4.证明 如图,过点E作FH∥AB,交AD的延长线于点F,交BC于点H.
∵AD∥BC,FH∥AB,∴四边形ABHF为平行四边形.∴S△ABE=S平行四边形ABHF.
∵AD∥BC,∴∠F=∠1,∠2=∠C.
∵E为DC的中点,∴DE=CE,∴△DEF≌△CEH(AAS),∴DF=HC,
∴ S平行四边形ABHF=S四边形ABCD.∴S△ABE=S四边形ABCD.
5.证明 连接ME,MF,NE,NF,如图所示:
∵E,M分别是AD,BD的中点,∴ME是△ABD的中位线,∴ME∥AB,
同理,MF∥CD,EN∥CD,FN∥AB,∴ME∥FN,MF∥EN,
∴四边形EMFN是平行四边形,∴EF与MN互相平分.
6.解析 (1)证明:如图,连接BD,AE,
∵FB=CE,∴BC=EF,又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB=∠DFE.
在△ABC和△DEF中,∴△ABC≌△DEF(ASA),∴AB=DE,
又∵AB// DE,∴四边形ABDE是平行四边形,∴AD与BE互相平分.
(2)∵FB=CE,∴BE=2BF+FC,∴,
∴AC=BF=3, BC=BF+FC=3+2-5,
∵AB⊥AC,∴由勾股定理得AB==4.
7.证明 ∵四边形ABCD是平行四边形,∴AB∥CD, 0A=OC, OB=OD,∴∠BAC=∠DCA.
又∵OA=0C,∠AOG=∠COH,∴△AOG≌△COH(ASA),∴0G=OH.
∴E,F分别为OB,OD的中点,∴0E=0B,OF=0D,∴OE=OF.
如图,连接GE,HF.
∵OG=OH,OE=OF,∴四边形EHFG是平行四边形,∴CF∥EH.
8.证明 如图,过点D作DE//B,交AB于点E,∴∠B=∠1.
∵AB∥CD,DE∥BC,∴四边形DEBC是平行四边形.∴∠B=∠CDE,CD=BE.
又∵∠ADC=2∠B=∠ADE+∠CDE,∴∠ADE=∠B=∠1.
∴AD=AE,∴AB=AE+EB=AD+CD.
9.证明 (1)延长CE交AB于点G,如图所示:
∵AE平分∠BAC,∴∠GAE=∠CAE.
∵ AE⊥CE,∴∠AEG=∠AEC=90°,
在△AGE和△ACE中,∴△AGE≌△ACE(ASA),∴GE=EC.
又∵D是边BC的中点,∴DE为△CGB的中位线,∴DE∥AB.
又∵EF∥BC,∴四边形BDEF是平行四边形.
(2)由(1)可知四边形BDEF是平行四边形,∴BF=DE.
∵D、E分别是BC、GC的中点,∴BF=DE=BG
∵△AGE≌△ACE,∴AG=AC,∴BF=(AB-AG)=(AB-AC).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
