4.1投影 同步练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第四章 投影与视图
1 投影
知识能力全练
知识点一 中心投影
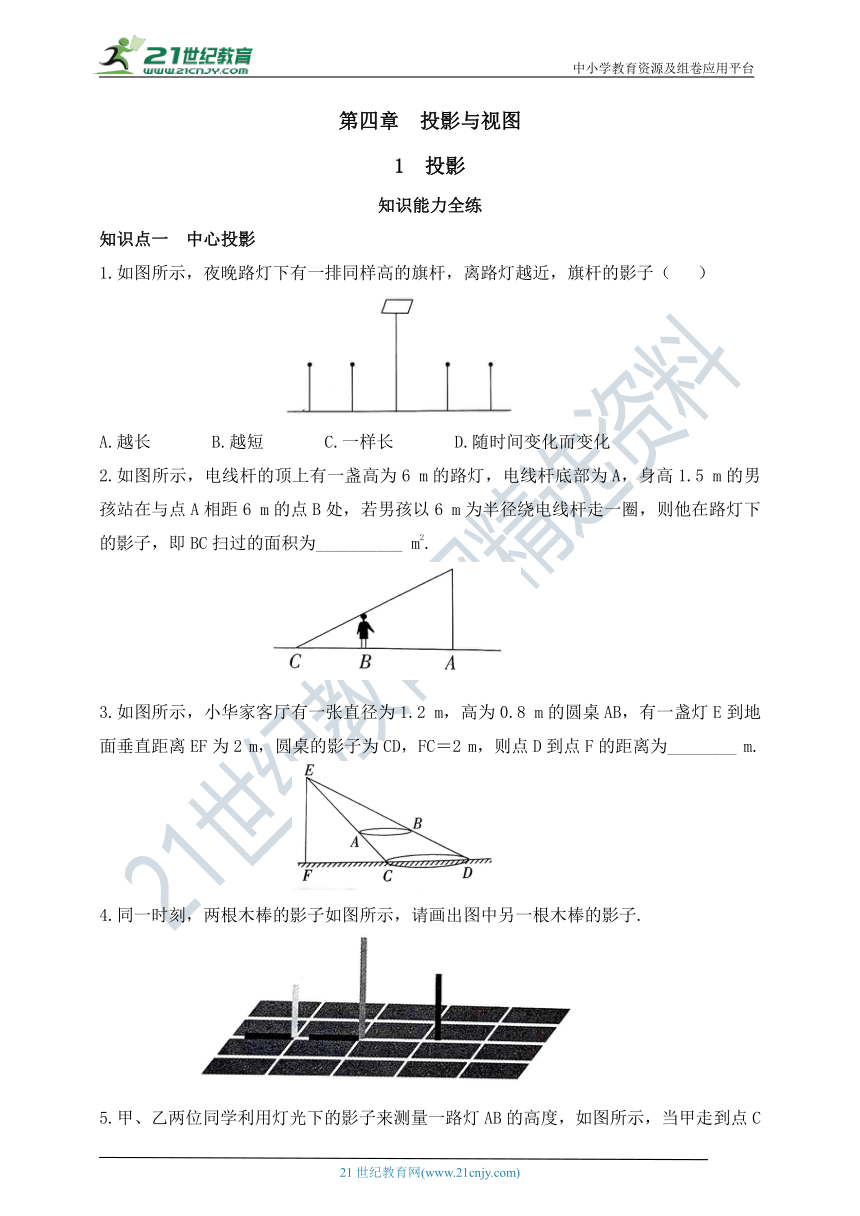
1.如图所示,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( )
A.越长 B.越短 C.一样长 D.随时间变化而变化
2.如图所示,电线杆的顶上有一盏高为6 m的路灯,电线杆底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处,若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子,即BC扫过的面积为__________ m2.
3.如图所示,小华家客厅有一张直径为1.2 m,高为0.8 m的圆桌AB,有一盏灯E到地面垂直距离EF为2 m,圆桌的影子为CD,FC=2 m,则点D到点F的距离为________ m.
4.同一时刻,两根木棒的影子如图所示,请画出图中另一根木棒的影子.
5.甲、乙两位同学利用灯光下的影子来测量一路灯AB的高度,如图所示,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5 m.已知甲直立时的身高为1.75 m,求路灯AB的高.(结果精确到0.1m)
知识点二 平行投影
6.下列投影中,是平行投影的是( )
A.路灯下行人的影子 B.太阳光下楼房的影子
C.台灯下书本的影子 D.在手电筒照射下纸片的影子
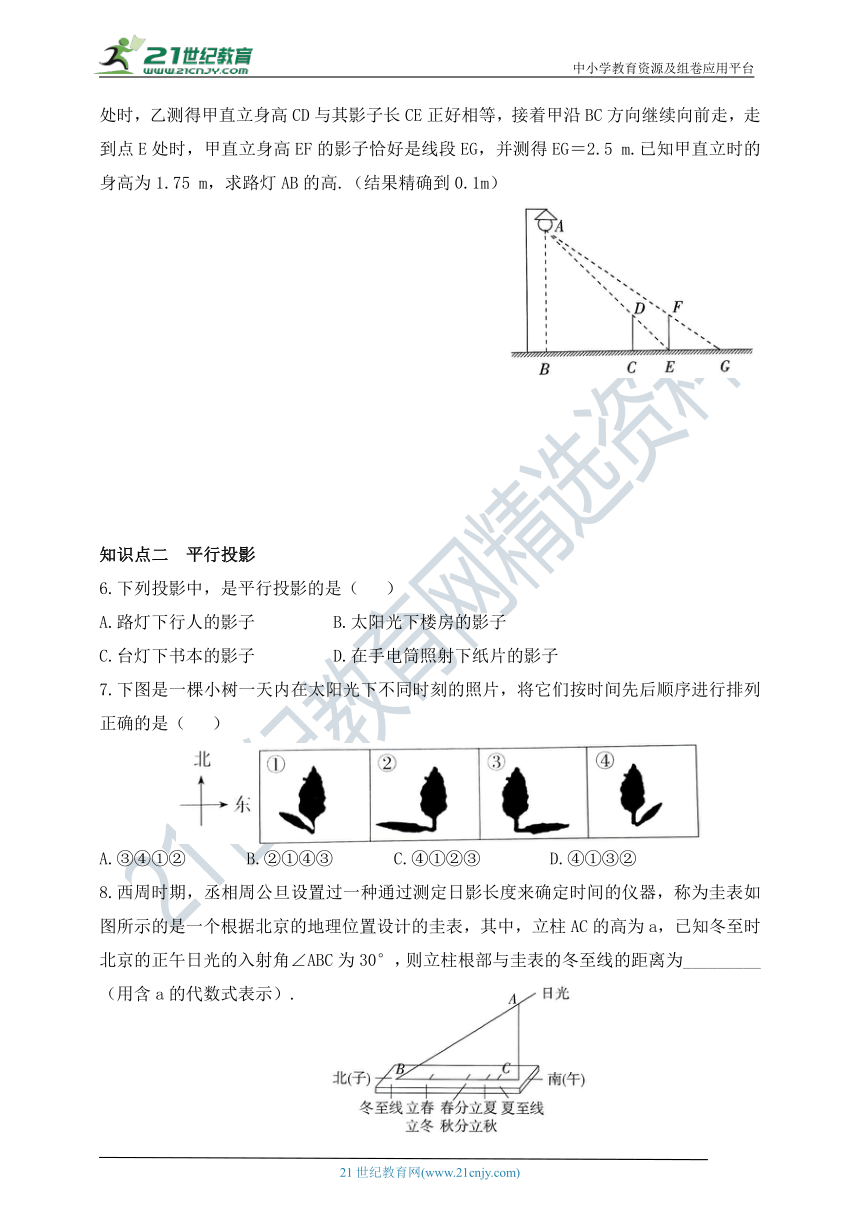
7.下图是一棵小树一天内在太阳光下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③④①② B.②①④③ C.④①②③ D.④①③②
8.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表如图所示的是一个根据北京的地理位置设计的圭表,其中,立柱AC的高为a,已知冬至时北京的正午日光的入射角∠ABC为30°,则立柱根部与圭表的冬至线的距离为_________(用含a的代数式表示).
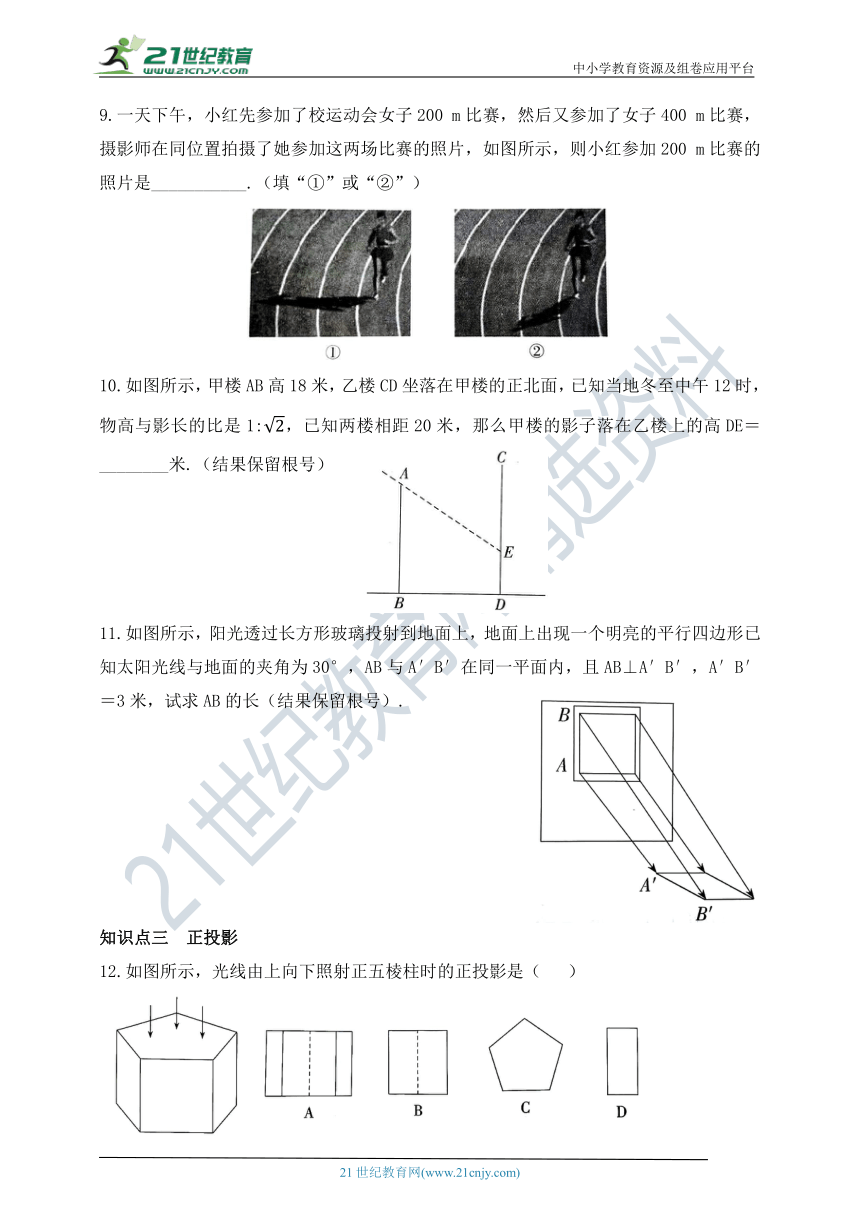
9.一天下午,小红先参加了校运动会女子200 m比赛,然后又参加了女子400 m比赛,摄影师在同位置拍摄了她参加这两场比赛的照片,如图所示,则小红参加200 m比赛的照片是___________.(填“①”或“②”)
10.如图所示,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE=________米.(结果保留根号)
11.如图所示,阳光透过长方形玻璃投射到地面上,地面上出现一个明亮的平行四边形已知太阳光线与地面的夹角为30°,AB与A′B′在同一平面内,且AB⊥A′B′,A′B′=3米,试求AB的长(结果保留根号).
知识点三 正投影
12.如图所示,光线由上向下照射正五棱柱时的正投影是( )
13.在阳光的照射下,一块三角板的投影不会是( )
A.线段 B.与原三角形全等的三角形 C.变形的三角形 D.点
巩固提高全练
14.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯同侧
C.他们站在路灯两侧 D.他们站在月光下
15.如图所示,在直角坐标系中,点P(3,2)是一个光源.木杆AB两端的坐标分别为(0,1),(4,1),则木杆AB在x轴上的投影长为( )
A.4 B.5 C.6 D.8
16.甲、乙两人在太阳光下并行,乙的身高是1.8 m,他的影长是2.1 m,甲比乙矮12 cm,此刻甲的影长是__________.
17.如图所示,小树AB在路灯O的照射下形成投影BC.若树高AB=2 m,树影BC=3 m,树与路灯的水平距离BP=4 m,则路灯的高度OP为_________ m.
18.如图所示,正方形纸板ABCD在投影面a上的正投影为矩形A1B1C1D1,其中边AB、CD与投影面平行,AD、BC与投影面不平行.若正方形ABCD的边长为5厘米,∠BCC1=45°,求其投影矩形A1B1C1D1的面积.
19.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
20.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时同地测得一栋楼的影
长为90 m,则这栋楼的高度为__________ m.
21.如图所示,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CG的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是______________(用“=”“>”或“<”连起来).
22.如图所示,一人在两等高的路灯之间走动,GB为人AB在路灯EF照射下的影子,BH为人AB在路灯CD照射下的影子当人从点C走向点E时两段影子之和GH的变化趋势是( )
A.先变长后变短 B.先变短后变长 C.不变 D.先变短后变长再变短
23.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图所示,此时测得地面上的影长为8米,坡面上的影长为4米已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,请计算出树的高度.
参考答案
1.B 2. 28 3. 4
4.解析 如图,线段AB即为另一根木棒的影子.
5.解析 设AB=x m.由题意知AB⊥BG,CD⊥BG,CD=CE,∴AB∥CD,
∴△ABE∽△DCE,∴=1,∴AB=BE=x m.
由题意知FE⊥BG,∴AB∥EF,∴△ABG∽△FEG,∴,即,
∴ .
答:路灯AB的高约为5.8 m.
6.B 7.B 8. a 9. ② 10. (18-10)
11.解析 如图,过点A作AC∥A′B′交BB′于C,
则AC=A′B′=3,∠ACB=30°,∠BAC=90°.
∴AB=AC·tan∠ACB=.
∴AB的长为米.
12.C 13.D 14.C 15.D 16. 1.96 m 17.
18.解析 由题意得A1B1=AB=5厘米,
B.C1=BC·sin45°=5×=(厘米).
∴矩形A1B1C1D1的面积=5×=(平方厘米).
答:投影矩形ABCD的面积是平方厘米.
19.C 20. 54 21. S1=S<S2 22.C
23.解析 如图,延长AC交直线BD于点F,过点C作CE⊥BF于点E.
在Rt△CDE中,CD=4米,∠CDE=30°,则CE=2米,所以DE=米.
根据同一时刻物高与影长对应成比例,得,则EF=4米,
所以BF=BD+DE+EF=8+2+4=(12+2)米.
又,所以AB=(6+)米,所以树的高度为(6+)米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 投影与视图
1 投影
知识能力全练
知识点一 中心投影
1.如图所示,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( )
A.越长 B.越短 C.一样长 D.随时间变化而变化
2.如图所示,电线杆的顶上有一盏高为6 m的路灯,电线杆底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处,若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子,即BC扫过的面积为__________ m2.
3.如图所示,小华家客厅有一张直径为1.2 m,高为0.8 m的圆桌AB,有一盏灯E到地面垂直距离EF为2 m,圆桌的影子为CD,FC=2 m,则点D到点F的距离为________ m.
4.同一时刻,两根木棒的影子如图所示,请画出图中另一根木棒的影子.
5.甲、乙两位同学利用灯光下的影子来测量一路灯AB的高度,如图所示,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5 m.已知甲直立时的身高为1.75 m,求路灯AB的高.(结果精确到0.1m)
知识点二 平行投影
6.下列投影中,是平行投影的是( )
A.路灯下行人的影子 B.太阳光下楼房的影子
C.台灯下书本的影子 D.在手电筒照射下纸片的影子
7.下图是一棵小树一天内在太阳光下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③④①② B.②①④③ C.④①②③ D.④①③②
8.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表如图所示的是一个根据北京的地理位置设计的圭表,其中,立柱AC的高为a,已知冬至时北京的正午日光的入射角∠ABC为30°,则立柱根部与圭表的冬至线的距离为_________(用含a的代数式表示).
9.一天下午,小红先参加了校运动会女子200 m比赛,然后又参加了女子400 m比赛,摄影师在同位置拍摄了她参加这两场比赛的照片,如图所示,则小红参加200 m比赛的照片是___________.(填“①”或“②”)
10.如图所示,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE=________米.(结果保留根号)
11.如图所示,阳光透过长方形玻璃投射到地面上,地面上出现一个明亮的平行四边形已知太阳光线与地面的夹角为30°,AB与A′B′在同一平面内,且AB⊥A′B′,A′B′=3米,试求AB的长(结果保留根号).
知识点三 正投影
12.如图所示,光线由上向下照射正五棱柱时的正投影是( )
13.在阳光的照射下,一块三角板的投影不会是( )
A.线段 B.与原三角形全等的三角形 C.变形的三角形 D.点
巩固提高全练
14.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯同侧
C.他们站在路灯两侧 D.他们站在月光下
15.如图所示,在直角坐标系中,点P(3,2)是一个光源.木杆AB两端的坐标分别为(0,1),(4,1),则木杆AB在x轴上的投影长为( )
A.4 B.5 C.6 D.8
16.甲、乙两人在太阳光下并行,乙的身高是1.8 m,他的影长是2.1 m,甲比乙矮12 cm,此刻甲的影长是__________.
17.如图所示,小树AB在路灯O的照射下形成投影BC.若树高AB=2 m,树影BC=3 m,树与路灯的水平距离BP=4 m,则路灯的高度OP为_________ m.
18.如图所示,正方形纸板ABCD在投影面a上的正投影为矩形A1B1C1D1,其中边AB、CD与投影面平行,AD、BC与投影面不平行.若正方形ABCD的边长为5厘米,∠BCC1=45°,求其投影矩形A1B1C1D1的面积.
19.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
20.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时同地测得一栋楼的影
长为90 m,则这栋楼的高度为__________ m.
21.如图所示,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CG的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是______________(用“=”“>”或“<”连起来).
22.如图所示,一人在两等高的路灯之间走动,GB为人AB在路灯EF照射下的影子,BH为人AB在路灯CD照射下的影子当人从点C走向点E时两段影子之和GH的变化趋势是( )
A.先变长后变短 B.先变短后变长 C.不变 D.先变短后变长再变短
23.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图所示,此时测得地面上的影长为8米,坡面上的影长为4米已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,请计算出树的高度.
参考答案
1.B 2. 28 3. 4
4.解析 如图,线段AB即为另一根木棒的影子.
5.解析 设AB=x m.由题意知AB⊥BG,CD⊥BG,CD=CE,∴AB∥CD,
∴△ABE∽△DCE,∴=1,∴AB=BE=x m.
由题意知FE⊥BG,∴AB∥EF,∴△ABG∽△FEG,∴,即,
∴ .
答:路灯AB的高约为5.8 m.
6.B 7.B 8. a 9. ② 10. (18-10)
11.解析 如图,过点A作AC∥A′B′交BB′于C,
则AC=A′B′=3,∠ACB=30°,∠BAC=90°.
∴AB=AC·tan∠ACB=.
∴AB的长为米.
12.C 13.D 14.C 15.D 16. 1.96 m 17.
18.解析 由题意得A1B1=AB=5厘米,
B.C1=BC·sin45°=5×=(厘米).
∴矩形A1B1C1D1的面积=5×=(平方厘米).
答:投影矩形ABCD的面积是平方厘米.
19.C 20. 54 21. S1=S<S2 22.C
23.解析 如图,延长AC交直线BD于点F,过点C作CE⊥BF于点E.
在Rt△CDE中,CD=4米,∠CDE=30°,则CE=2米,所以DE=米.
根据同一时刻物高与影长对应成比例,得,则EF=4米,
所以BF=BD+DE+EF=8+2+4=(12+2)米.
又,所以AB=(6+)米,所以树的高度为(6+)米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
