2021-2022学年河北省唐山市古冶区九年级(上)期中数学试卷(Word版 无答案)
文档属性
| 名称 | 2021-2022学年河北省唐山市古冶区九年级(上)期中数学试卷(Word版 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 07:50:25 | ||
图片预览

文档简介
2021-2022学年河北省唐山市古冶区九年级(上)期中数学试卷
一、选择题(本大题共16个小题,每小题2分,共32分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若方程(a﹣3)x2+x+a=0是关于x的一元二次方程,则( )
A.a≠0 B.a≠3 C.a>0 D.a>3
2.下列四个图形中,可以看作是中心对称图的是( )
A. B.
C. D.
3.已知⊙O的半径为5,点A为线段OP的中点,当OP=12时,点A与⊙O的位置关系是( )
A.在圆内 B.在圆上 C.在圆外 D.不能确定
4.下列方程中,没有实数根( )
A.x2+2x=0 B.x2+2x+1=0 C.x2+2x﹣1=0 D.x2+2x+2=0
5.用配方法解方程x2﹣8x+3=0时,原方程应变形为( )
A.(x﹣4)2=13 B.(x﹣4)2=3 C.(x+4)2=13 D.(x+4)2=3
6.在图形的旋转中,下列说法不正确的是( )
A.旋转前和旋转后的图形全等
B.图形上的每一个点到旋转中心的距离都相等
C.对应点与旋转中心所连线段的夹角等于旋转角
D.图形上可能存在不动的点
7.将抛物线y=3x2向右平移2个单位,得到新抛物线的解析式为( )
A.y=3(x﹣2)2 B.y=3x2+2 C.y=3(x+2)2 D.y=3x2﹣2
8.设方程x2﹣3x+2=0的两根分别是x1,x2,则x1 x2=( )
A.﹣3 B.2 C.﹣2 D.3
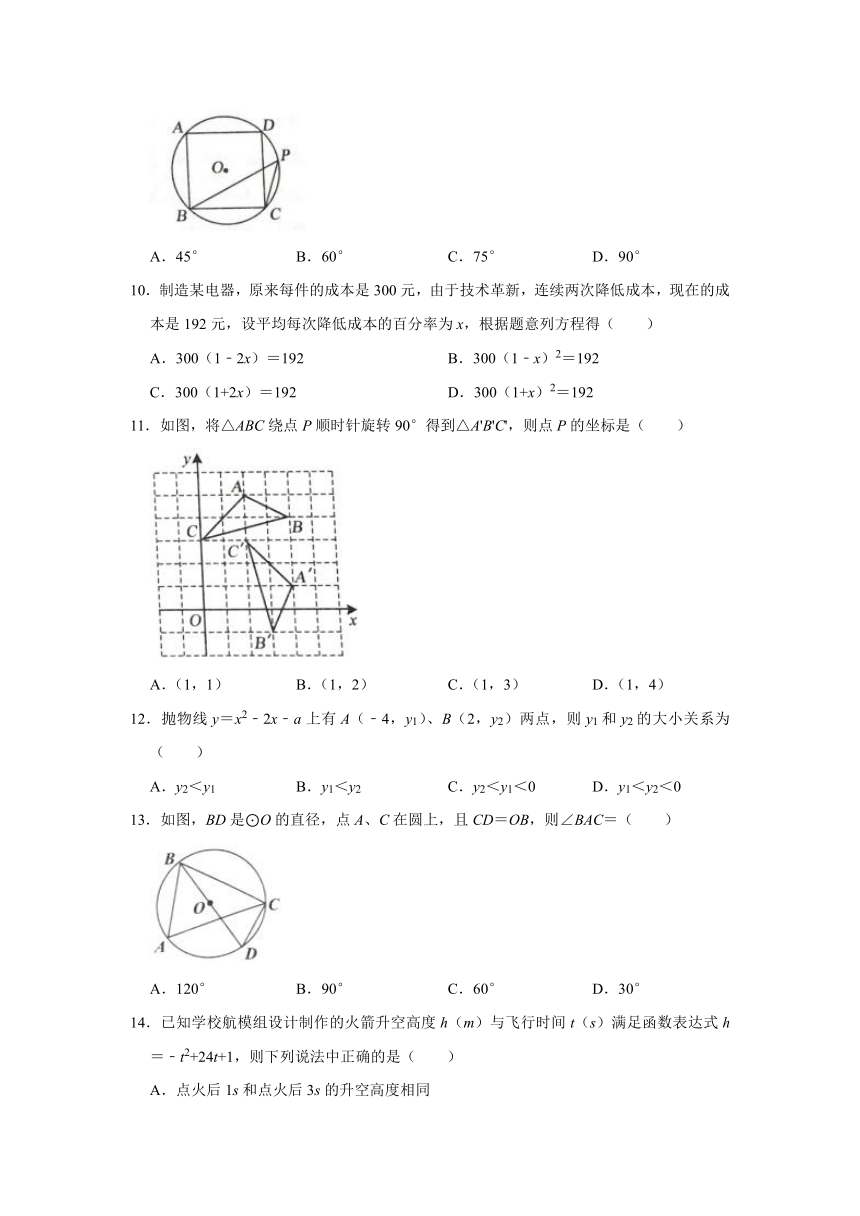
9.如图,正方形ABCD的四个顶点分别在⊙O上,点P是弧CD上不同于点C的任意一点,则∠BPC=( )
A.45° B.60° C.75° D.90°
10.制造某电器,原来每件的成本是300元,由于技术革新,连续两次降低成本,现在的成本是192元,设平均每次降低成本的百分率为x,根据题意列方程得( )
A.300(1﹣2x)=192 B.300(1﹣x)2=192
C.300(1+2x)=192 D.300(1+x)2=192
11.如图,将△ABC绕点P顺时针旋转90°得到△A'B'C',则点P的坐标是( )
A.(1,1) B.(1,2) C.(1,3) D.(1,4)
12.抛物线y=x2﹣2x﹣a上有A(﹣4,y1)、B(2,y2)两点,则y1和y2的大小关系为( )
A.y2<y1 B.y1<y2 C.y2<y1<0 D.y1<y2<0
13.如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠BAC=( )
A.120° B.90° C.60° D.30°
14.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
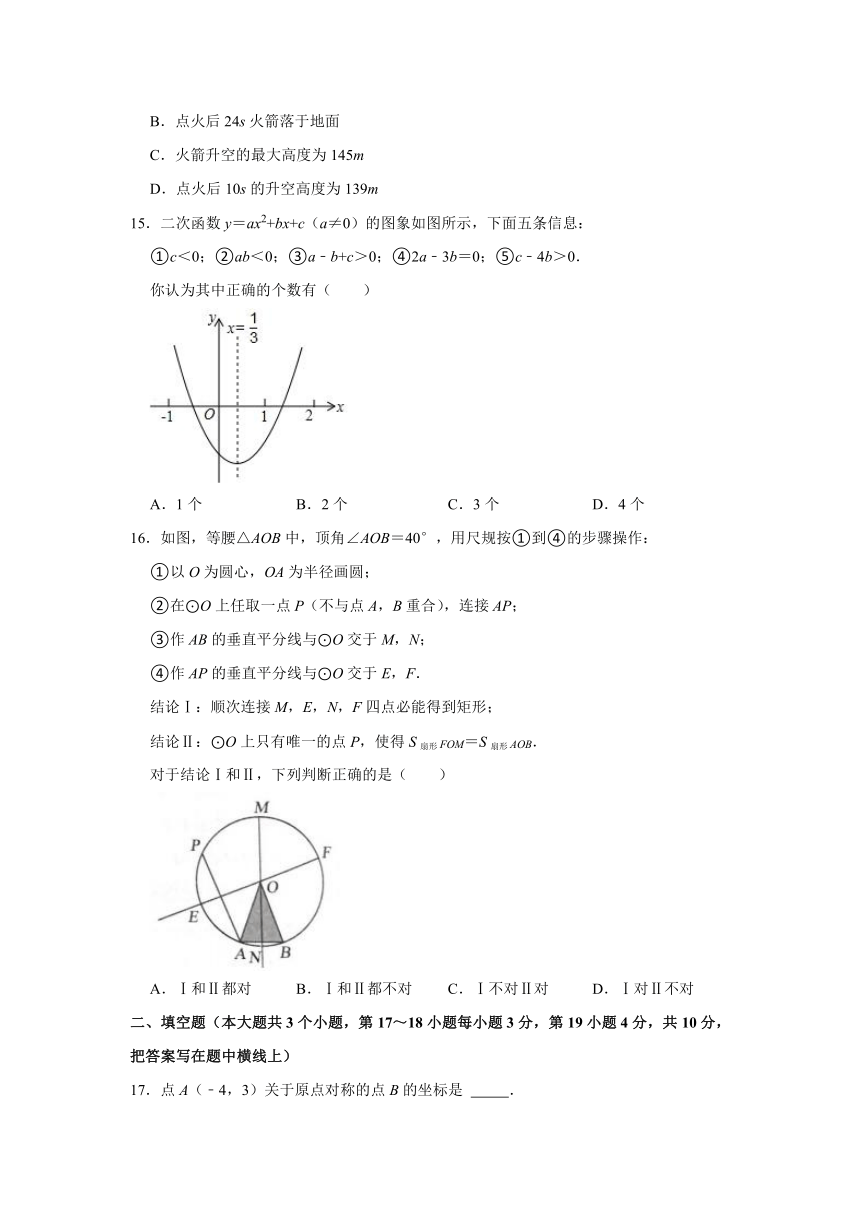
15.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下面五条信息:
①c<0;②ab<0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0.
你认为其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
16.如图,等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形;
结论Ⅱ:⊙O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
二、填空题(本大题共3个小题,第17~18小题每小题3分,第19小题4分,共10分,把答案写在题中横线上)
17.点A(﹣4,3)关于原点对称的点B的坐标是 .
18.抛物线y=x2﹣x﹣1与x轴的一个交点的坐标为(m,0),则代数式m2﹣m+2021= .
19.如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,则∠AMB= 度;过点N的直线l∥BC,则∠1= 度.
三、解答题(本大题共7个小题,共58分。解答应写出文字说明、证明过程或演算步骤)
20.解方程:
(1)3x2﹣6=0;
(2)x2+x﹣6=0.
21.已知:二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3用配方法化成y=a(x﹣h)2+k的形式,并直接写出抛物线的开口方向和顶点坐标;
(2)求此函数图象与x轴、y轴的交点坐标.
22.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点O为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)将△ABC以点C为旋转中心顺时针旋转90°可以得到△A2B2C,画出△A2B2C并直接写出A1A2的长度.
23.如图,在长60米,宽40米的长方形花园中,欲修宽度相等的观赏路(图中阴影部分),要使观赏路面积占总面积的,求观赏路面宽是多少米?
24.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
25.如图,⊙O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作⊙O的切线交A1A11延长线于点P.
(1)通过计算比较直径和劣弧长度哪个更长;
(2)连接A7A11,则A7A11和PA1有什么特殊位置关系?请简要说明理由;
(3)求切线长PA7的值.
26.如图,直线yx+2交y轴于点A,交x轴于点C,抛物线yx2+bx+c经过点A,点C,且交x轴于另一点B.
(1)点A的坐标为 ,点C的坐标为 ,并求抛物线的解析式;
(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;
(3)将线段OA绕x轴上的动点P(m,0)顺时针旋转90°得到线段O1A1,若线段O1A1与抛物线只有一个公共点,请你直接写出m的取值范围.
一、选择题(本大题共16个小题,每小题2分,共32分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若方程(a﹣3)x2+x+a=0是关于x的一元二次方程,则( )
A.a≠0 B.a≠3 C.a>0 D.a>3
2.下列四个图形中,可以看作是中心对称图的是( )
A. B.
C. D.
3.已知⊙O的半径为5,点A为线段OP的中点,当OP=12时,点A与⊙O的位置关系是( )
A.在圆内 B.在圆上 C.在圆外 D.不能确定
4.下列方程中,没有实数根( )
A.x2+2x=0 B.x2+2x+1=0 C.x2+2x﹣1=0 D.x2+2x+2=0
5.用配方法解方程x2﹣8x+3=0时,原方程应变形为( )
A.(x﹣4)2=13 B.(x﹣4)2=3 C.(x+4)2=13 D.(x+4)2=3
6.在图形的旋转中,下列说法不正确的是( )
A.旋转前和旋转后的图形全等
B.图形上的每一个点到旋转中心的距离都相等
C.对应点与旋转中心所连线段的夹角等于旋转角
D.图形上可能存在不动的点
7.将抛物线y=3x2向右平移2个单位,得到新抛物线的解析式为( )
A.y=3(x﹣2)2 B.y=3x2+2 C.y=3(x+2)2 D.y=3x2﹣2
8.设方程x2﹣3x+2=0的两根分别是x1,x2,则x1 x2=( )
A.﹣3 B.2 C.﹣2 D.3
9.如图,正方形ABCD的四个顶点分别在⊙O上,点P是弧CD上不同于点C的任意一点,则∠BPC=( )
A.45° B.60° C.75° D.90°
10.制造某电器,原来每件的成本是300元,由于技术革新,连续两次降低成本,现在的成本是192元,设平均每次降低成本的百分率为x,根据题意列方程得( )
A.300(1﹣2x)=192 B.300(1﹣x)2=192
C.300(1+2x)=192 D.300(1+x)2=192
11.如图,将△ABC绕点P顺时针旋转90°得到△A'B'C',则点P的坐标是( )
A.(1,1) B.(1,2) C.(1,3) D.(1,4)
12.抛物线y=x2﹣2x﹣a上有A(﹣4,y1)、B(2,y2)两点,则y1和y2的大小关系为( )
A.y2<y1 B.y1<y2 C.y2<y1<0 D.y1<y2<0
13.如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠BAC=( )
A.120° B.90° C.60° D.30°
14.已知学校航模组设计制作的火箭升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1,则下列说法中正确的是( )
A.点火后1s和点火后3s的升空高度相同
B.点火后24s火箭落于地面
C.火箭升空的最大高度为145m
D.点火后10s的升空高度为139m
15.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下面五条信息:
①c<0;②ab<0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0.
你认为其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
16.如图,等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形;
结论Ⅱ:⊙O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
二、填空题(本大题共3个小题,第17~18小题每小题3分,第19小题4分,共10分,把答案写在题中横线上)
17.点A(﹣4,3)关于原点对称的点B的坐标是 .
18.抛物线y=x2﹣x﹣1与x轴的一个交点的坐标为(m,0),则代数式m2﹣m+2021= .
19.如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,则∠AMB= 度;过点N的直线l∥BC,则∠1= 度.
三、解答题(本大题共7个小题,共58分。解答应写出文字说明、证明过程或演算步骤)
20.解方程:
(1)3x2﹣6=0;
(2)x2+x﹣6=0.
21.已知:二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3用配方法化成y=a(x﹣h)2+k的形式,并直接写出抛物线的开口方向和顶点坐标;
(2)求此函数图象与x轴、y轴的交点坐标.
22.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点O为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)将△ABC以点C为旋转中心顺时针旋转90°可以得到△A2B2C,画出△A2B2C并直接写出A1A2的长度.
23.如图,在长60米,宽40米的长方形花园中,欲修宽度相等的观赏路(图中阴影部分),要使观赏路面积占总面积的,求观赏路面宽是多少米?
24.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
25.如图,⊙O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作⊙O的切线交A1A11延长线于点P.
(1)通过计算比较直径和劣弧长度哪个更长;
(2)连接A7A11,则A7A11和PA1有什么特殊位置关系?请简要说明理由;
(3)求切线长PA7的值.
26.如图,直线yx+2交y轴于点A,交x轴于点C,抛物线yx2+bx+c经过点A,点C,且交x轴于另一点B.
(1)点A的坐标为 ,点C的坐标为 ,并求抛物线的解析式;
(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;
(3)将线段OA绕x轴上的动点P(m,0)顺时针旋转90°得到线段O1A1,若线段O1A1与抛物线只有一个公共点,请你直接写出m的取值范围.
同课章节目录
