2021--2022学年人教版(2012)八年级上册数学12.3角的平分线的性质 尖子生培优练(word解析版)
文档属性
| 名称 | 2021--2022学年人教版(2012)八年级上册数学12.3角的平分线的性质 尖子生培优练(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 581.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 18:00:30 | ||
图片预览

文档简介
12.3角的平分线的性质尖子生培优练--2021--2022人教版(2012)八年级上学期第十二章全等三角形
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列说法中,正确的是( )
A.一条射线把一个角分成两个角,这条射线叫做这个角的平分线
B.P是直线外一点,A,B,C分别是上的三点,已知PA=1,PB=2,PC=3,则点P到直线的距离一定是1
C.相等的角是对顶角
D.钝角的补角一定是锐角
2.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
A.1 B.2 C. D.4
3.如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( )
A. B. C. D.
4.如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
A.40° B.50° C.30° D.45°
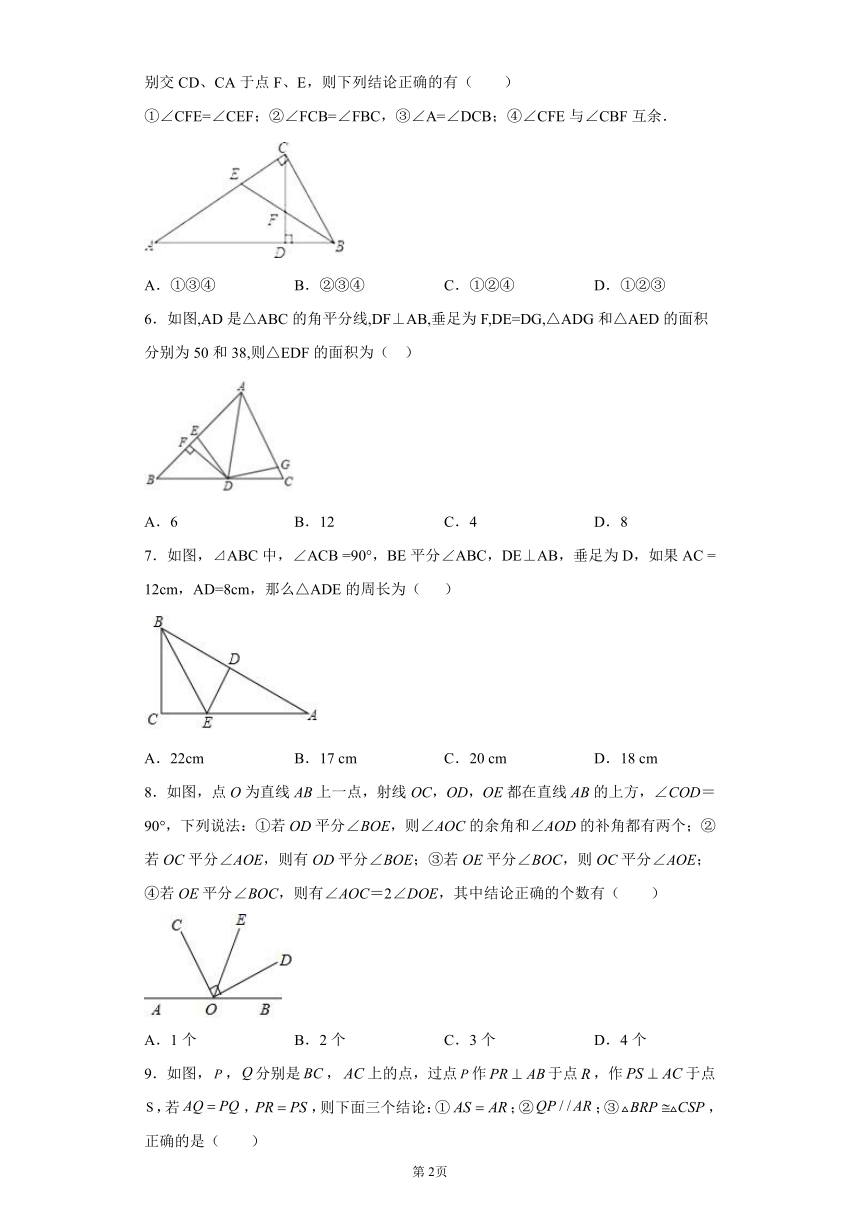
5.如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
①∠CFE=∠CEF;②∠FCB=∠FBC,③∠A=∠DCB;④∠CFE与∠CBF互余.
A.①③④ B.②③④ C.①②④ D.①②③
6.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.6 B.12 C.4 D.8
7.如图,⊿ABC中,∠ACB =90°,BE平分∠ABC,DE⊥AB,垂足为D,如果AC = 12cm,AD=8cm,那么△ADE的周长为( )
A.22cm B.17 cm C.20 cm D.18 cm
8.如图,点O为直线AB上一点,射线OC,OD,OE都在直线AB的上方,∠COD=90°,下列说法:①若OD平分∠BOE,则∠AOC的余角和∠AOD的补角都有两个;②若OC平分∠AOE,则有OD平分∠BOE;③若OE平分∠BOC,则OC平分∠AOE;④若OE平分∠BOC,则有∠AOC=2∠DOE,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
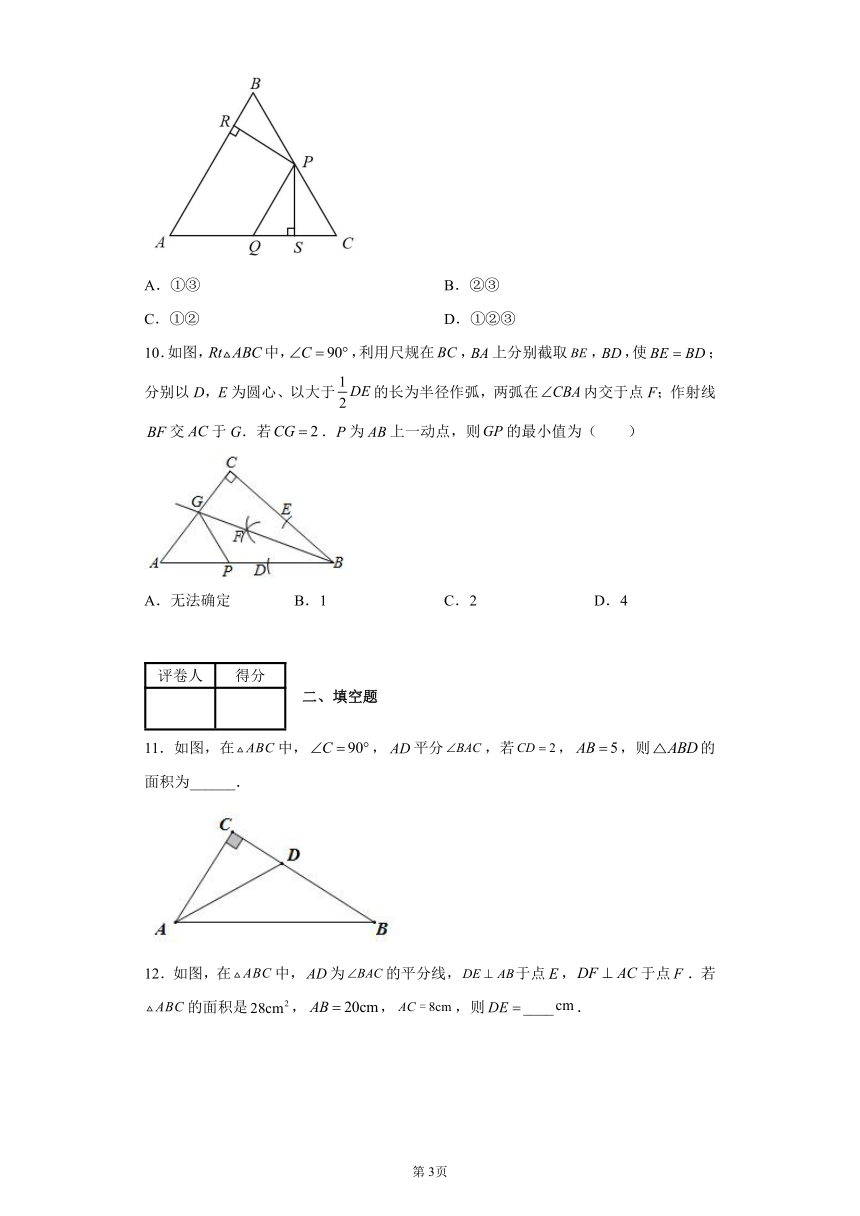
9.如图,,分别是,上的点,过点作于点,作于点,若,,则下面三个结论:①;②;③,正确的是( )
A.①③ B.②③
C.①② D.①②③
10.如图,中,,利用尺规在,上分别截取,,使;分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线交于G.若.P为上一动点,则的最小值为( )
A.无法确定 B.1 C.2 D.4
评卷人得分
二、填空题
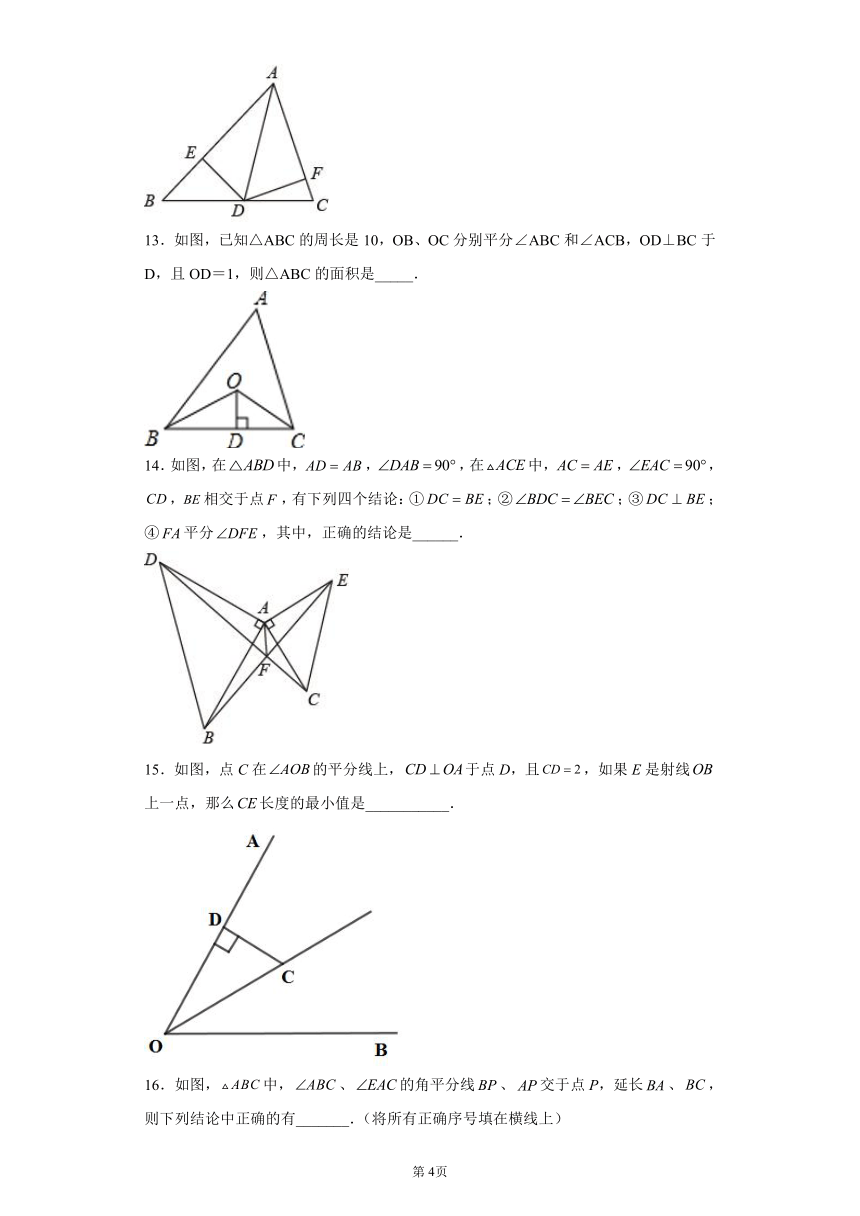
11.如图,在中,,平分,若,,则的面积为______.
12.如图,在中,为的平分线,于点,于点.若的面积是,,,则____.
13.如图,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是_____.
14.如图,在中,,,在中,,,,相交于点,有下列四个结论:①;②;③;④平分,其中,正确的结论是______.
15.如图,点C在的平分线上,于点D,且,如果E是射线上一点,那么长度的最小值是___________.
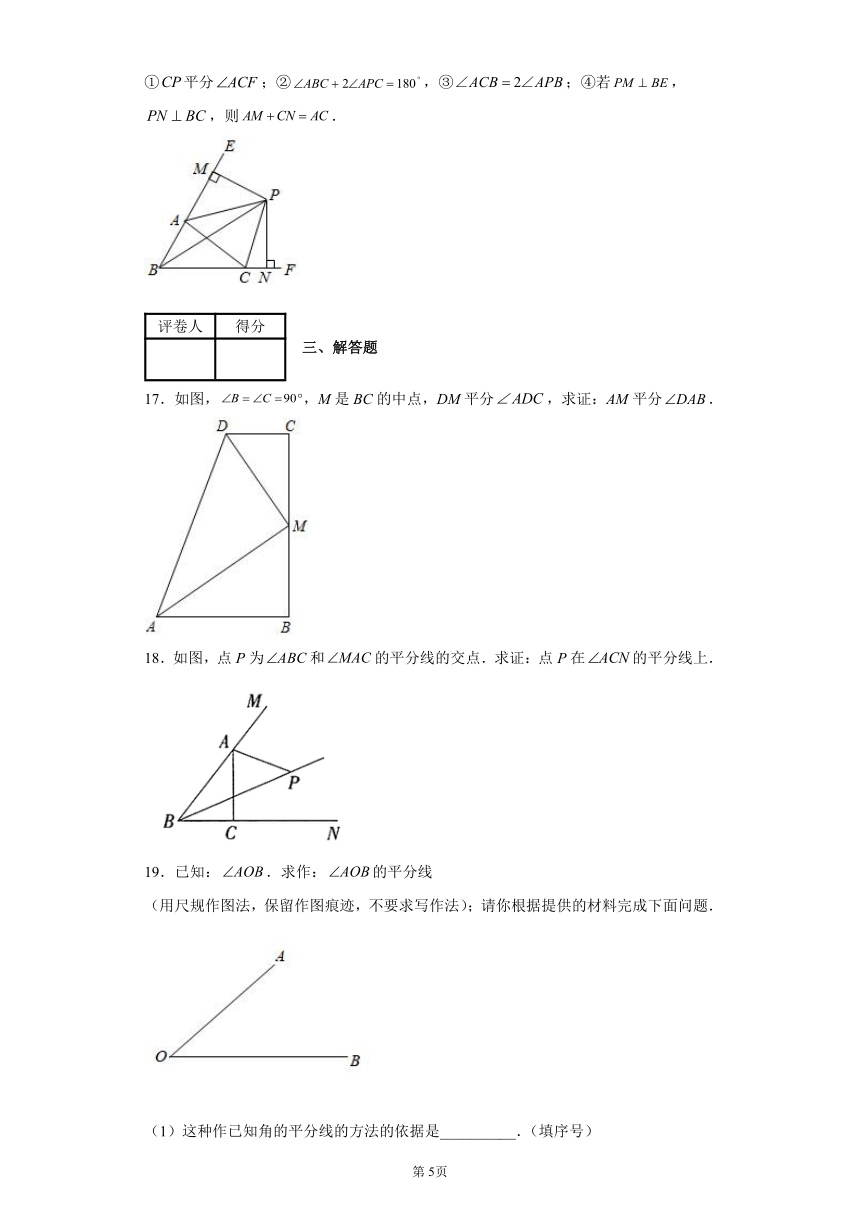
16.如图,中,、的角平分线、交于点P,延长、,则下列结论中正确的有_______.(将所有正确序号填在横线上)
①平分;②,③;④若,,则.
评卷人得分
三、解答题
17.如图,,M是BC的中点,DM平分,求证:AM平分.
18.如图,点P为和的平分线的交点.求证:点P在的平分线上.
19.已知:.求作:的平分线
(用尺规作图法,保留作图痕迹,不要求写作法);请你根据提供的材料完成下面问题.
(1)这种作已知角的平分线的方法的依据是__________.(填序号)
①②③④
(2)请你证明为的平分线.
20.如图,已知AB∥CD,CE平分∠ACD,CF⊥CE,∠1=34°.
(1)求∠ACE的度数;
(2)若∠2=56°,求证:CF∥AG.
21.已知:∠DEC+∠C=180°,DE平分∠ADF,∠F=∠1.求证:∠B=∠C.
22.如图,在中,点D是延长线上的一点,过点D作,平分,平分,与交于点G.
(1)证明:;
(2)如图1,若,求的度数;
(3)如图2,连接,若.求证:.
试卷第1页,共3页
第1页
答案与提示
1.D
【解】
A.分成的两个角不一定相等,不符合题意;
B.PA不一定与l垂直,不符合题意;
C.相等的两个角不一定是对顶角,不符合题意;
D.钝角的补角一定是锐角,符合题意.
故选D.
2.B
【解】
如图,过点P作,垂足为点G,根据角平分线上的点到角的两边距离相等可得,.
故选B.
3.B
解:根据题意,三角形的两角和他们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形
故选:B
4.A
解:∵AB//CD,∠DCB=100°,
∴∠DCB+∠ABC=180°,
∴∠ABC=80°,
∵BD平分∠ABC,
∴∠ABD=40°,
∵AB//CD,
∴∠D=∠ABD=40°,
故选A.
5.A
【解】
如图所示,
①∵BE平分∠ABC,
∴∠5=∠6,
∵∠3+∠4=90°,∠A+∠3=90°,
∴∠A=∠4,
∵∠1=∠A+∠6,∠2=∠4+∠5,
∠1=∠2,
故∠CFE=∠CEF,所以①正确;
②若∠FCB=∠FBC,即∠4=∠5,
由(1)可知:∠A=∠4,
∴∠A=∠5=∠6,
∵∠A+∠5+∠6=180°,
∴∠A=30°,
即只有当∠A=30°时,∠FCB=∠FBC而已知没有这个条件,故②错误;
③∵∠3+∠4=90°,∠A+∠3=90°,
∴∠A=∠4,
即∠A=∠DCB,故③正确;
④∵∠1=∠2,∠1+∠5=90°,
∴∠2+∠5=90°,
即:∠CFE与∠CBF互余,故④正确.
故选A.
6.A
【解】
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,设面积为S,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH,
即38+S=50-S,
解得S=6.
故选A.
7.C
【解】:∵∠ACB=90°,
∴EC⊥BC,
又∵BE平分∠ABC,DE⊥AB,
∴DE=CE,
又∵AC=12cm,
∴AE+DE=AE+CE=AC=12cm.
∴AE+DE+ADF=(AE+CE)+AD=AC+AD=12+8=20cm.
故选C.
8.C
解:①若OD平分∠BOE,则∠BOD=∠DOE,
∵∠COD=90°,
∴∠AOC+∠BOD=90°,∠AOC+∠DOE=90°,
又∵∠AOD+∠BOD=180°,∠AOD+∠DOE=180°,
∴∠AOC的余角和∠AOD的补角都有两个,
故①正确;
②若OC平分∠AOE,则∠AOC=∠EOC,
又∵∠COD=90°,
∴∠AOC+∠BOD=90°,∠COE+∠DOE=90°,
∴∠DOE=∠DOB,
∴OD平分∠BOE,
故②正确;
③若OE平分∠BOC,则OC平分∠AOE不一定成立,
故③错误;
④若OE平分∠BOC,则∠BOE=∠BOC=(180° ∠AOC)=90° ∠AOC,
又∵∠DOB=90° ∠AOC,
∴∠DOE=∠BOE ∠BOD=(90° ∠AOC) (90° ∠AOC)=∠AOC,
∴∠AOC=2∠DOE,
故④正确;故选:C.
9.C
解:如图示,连接,
,
是的平分线,
,①正确.
,②正确.
只是过点,并没有固定,明显③不成立.
故选:.
10.C
解:作GH⊥AB
由题意可知:BG是∠ABC的角平分线
又∵GH⊥AB,
∴CG=GH
∵
∴GH=2
由直线外一点到直线上各点的连线中,垂线段最短可得:
当点GP⊥AB时,有最小值
即= GH=2时,最短
故选:C
11.5
解:如图,过点D作DE⊥AB于点E,
∵,
∴AC⊥BC,
∵平分,
∴DE=CD=2,
∵,
∴的面积为 .
故答案为:5.
12.2
解:在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB DE+AC DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴×20DE+×8DF=10DE+4DF=14DE=28,
解得DE=2cm.
故答案为:2.
13.5
解:连接OA,过点O作OG⊥AB于G,OH⊥AC于H,
∵△ABC的周长是10,
∴AB+BC+AC=10,
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC,OG⊥AB,OH⊥AC,
∴OG=OH=OD=1,
∴△ABC的面积=△ABO的面积+△OBC的面积+△AOC的面积
=×AB×OG+×BC×OD+×AC×OH
=
=×10×1
=5,
故答案为:5.
14.①③④.
解:∵∠DAB=∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,∠ADB+∠ABD=90°,
∴∠DAC=∠BAE,
又AD=AB,AE=AC,
∴△DAC≌△BAE(SAS),
∴DC=BE,故①正确;
且∠ADC=∠ABE,
∴∠DFE=∠DBF+∠BDF=∠ABE+∠ABD+∠BDF=∠ABD+∠ADC+∠BDF=∠ABD+∠ADB=90°,
∴DC⊥BE,故③正确;
过A作AM⊥CD于M,AN⊥BE于N,
∴AM=AN,
∴FA平分∠DFE,故④正确;
无法通过已知条件和图形证明②正确,
故正确的结论是①③④,
故答案为:①③④.
15.2
解:如图,
由垂线段最短定理可知:当CE⊥OB时,CE 的长度最小,
∵点C在 ∠AOB 的平分线上,CD⊥OA,
∴CE=CD=2,
故答案为2 .
16.①②③④
解:①作PD⊥AC于D.
∵PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上,故①正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
在Rt△PAM和Rt△PAD中,
,
∴Rt△PAM≌Rt△PAD(HL),
∴∠APM=∠APD,
同理:Rt△PCD≌Rt△PCN(HL),
∴∠CPD=∠CPN,
∴∠MPN=2∠APC,
∴∠ABC+2∠APC=180°,②正确;
③∵PA平分∠CAE,BP平分∠ABC,
∴∠CAE=2∠PAM,
∵∠CAE=∠ABC+∠ACB,∠PAM=∠ABC+∠APB,
∴∠ACB=2∠APB,③正确;
④∵Rt△PAM≌Rt△PAD(已证),
∴AD=AM,
∵Rt△PCD≌Rt△PCN(已证),
∴CD=CN,
∴AM+CN=AD+CD=AC,④正确;
故答案为:①②③④.
17.见解析
解:如图,过点M作ME⊥AD于F,
∵∠C=90°,DM平分∠ADC,
∴ME=MC,
∵M是BC的中点,
∴BM=CM,
∴BM=EM,
又∵∠B=90°,
∴点M在∠BAD的平分线上,
∴AM平分∠DAB.
18.解析:欲证点P在的平分线上,只需证明点P到AC与CN的距离相等即可,可以分别作出点P到BM,AC,CN的垂线,结合题意证明即可.
答案:证明:如图,过点P作于点E,于点F,于点G,
∵点P为和的平分线的交点,
∴,,∴,
∴点P在的平分线上.
19.解:以为圆心,以任意长为半径作弧,交于两点,
再分别以点为圆心,以大于长为半径作弧,两弧在角的内部交于点,作射线,则为的角平分线,如下图:
(1)连接,如下图:
由作图可知:、、(公共边)
通过三角形三边相等求得
故答案为①
(2)在和中
∴
∴,即为的平分线
20.解:(1)∵AB∥CD
∴∠1=∠DCE=34°
∵CE平分∠ACD
∴∠ACE=∠DCE=34°
(2)∵CF⊥CE
∴∠FCE=90°
∴∠FCH=90°°=56°
∵∠2=56°
∴∠FCH=∠2
∴CF∥AG.
21解:证明:∵∠DEC+∠C=180°,∠F=∠1,
∴DEBC,ACDF,
∴∠ADE=∠B,∠EDF=∠BGD,∠C=∠BGD,
∴∠C=∠EDF,
∵DE平分∠ADF,
∴∠ADE=∠EDF,
∴∠B=∠C.
22.【解】
(1)∵中,,
∴,
又∵,,
∴;
(2)在延长线上标上点M,如图1所示.
∵,∴,.
∵平分,平分,
∴,,
∴,
∴.
(3)证明:如图2,由(2)知:,,
∵,
∴.
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.下列说法中,正确的是( )
A.一条射线把一个角分成两个角,这条射线叫做这个角的平分线
B.P是直线外一点,A,B,C分别是上的三点,已知PA=1,PB=2,PC=3,则点P到直线的距离一定是1
C.相等的角是对顶角
D.钝角的补角一定是锐角
2.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
A.1 B.2 C. D.4
3.如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( )
A. B. C. D.
4.如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
A.40° B.50° C.30° D.45°
5.如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
①∠CFE=∠CEF;②∠FCB=∠FBC,③∠A=∠DCB;④∠CFE与∠CBF互余.
A.①③④ B.②③④ C.①②④ D.①②③
6.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.6 B.12 C.4 D.8
7.如图,⊿ABC中,∠ACB =90°,BE平分∠ABC,DE⊥AB,垂足为D,如果AC = 12cm,AD=8cm,那么△ADE的周长为( )
A.22cm B.17 cm C.20 cm D.18 cm
8.如图,点O为直线AB上一点,射线OC,OD,OE都在直线AB的上方,∠COD=90°,下列说法:①若OD平分∠BOE,则∠AOC的余角和∠AOD的补角都有两个;②若OC平分∠AOE,则有OD平分∠BOE;③若OE平分∠BOC,则OC平分∠AOE;④若OE平分∠BOC,则有∠AOC=2∠DOE,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
9.如图,,分别是,上的点,过点作于点,作于点,若,,则下面三个结论:①;②;③,正确的是( )
A.①③ B.②③
C.①② D.①②③
10.如图,中,,利用尺规在,上分别截取,,使;分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线交于G.若.P为上一动点,则的最小值为( )
A.无法确定 B.1 C.2 D.4
评卷人得分
二、填空题
11.如图,在中,,平分,若,,则的面积为______.
12.如图,在中,为的平分线,于点,于点.若的面积是,,,则____.
13.如图,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是_____.
14.如图,在中,,,在中,,,,相交于点,有下列四个结论:①;②;③;④平分,其中,正确的结论是______.
15.如图,点C在的平分线上,于点D,且,如果E是射线上一点,那么长度的最小值是___________.
16.如图,中,、的角平分线、交于点P,延长、,则下列结论中正确的有_______.(将所有正确序号填在横线上)
①平分;②,③;④若,,则.
评卷人得分
三、解答题
17.如图,,M是BC的中点,DM平分,求证:AM平分.
18.如图,点P为和的平分线的交点.求证:点P在的平分线上.
19.已知:.求作:的平分线
(用尺规作图法,保留作图痕迹,不要求写作法);请你根据提供的材料完成下面问题.
(1)这种作已知角的平分线的方法的依据是__________.(填序号)
①②③④
(2)请你证明为的平分线.
20.如图,已知AB∥CD,CE平分∠ACD,CF⊥CE,∠1=34°.
(1)求∠ACE的度数;
(2)若∠2=56°,求证:CF∥AG.
21.已知:∠DEC+∠C=180°,DE平分∠ADF,∠F=∠1.求证:∠B=∠C.
22.如图,在中,点D是延长线上的一点,过点D作,平分,平分,与交于点G.
(1)证明:;
(2)如图1,若,求的度数;
(3)如图2,连接,若.求证:.
试卷第1页,共3页
第1页
答案与提示
1.D
【解】
A.分成的两个角不一定相等,不符合题意;
B.PA不一定与l垂直,不符合题意;
C.相等的两个角不一定是对顶角,不符合题意;
D.钝角的补角一定是锐角,符合题意.
故选D.
2.B
【解】
如图,过点P作,垂足为点G,根据角平分线上的点到角的两边距离相等可得,.
故选B.
3.B
解:根据题意,三角形的两角和他们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形
故选:B
4.A
解:∵AB//CD,∠DCB=100°,
∴∠DCB+∠ABC=180°,
∴∠ABC=80°,
∵BD平分∠ABC,
∴∠ABD=40°,
∵AB//CD,
∴∠D=∠ABD=40°,
故选A.
5.A
【解】
如图所示,
①∵BE平分∠ABC,
∴∠5=∠6,
∵∠3+∠4=90°,∠A+∠3=90°,
∴∠A=∠4,
∵∠1=∠A+∠6,∠2=∠4+∠5,
∠1=∠2,
故∠CFE=∠CEF,所以①正确;
②若∠FCB=∠FBC,即∠4=∠5,
由(1)可知:∠A=∠4,
∴∠A=∠5=∠6,
∵∠A+∠5+∠6=180°,
∴∠A=30°,
即只有当∠A=30°时,∠FCB=∠FBC而已知没有这个条件,故②错误;
③∵∠3+∠4=90°,∠A+∠3=90°,
∴∠A=∠4,
即∠A=∠DCB,故③正确;
④∵∠1=∠2,∠1+∠5=90°,
∴∠2+∠5=90°,
即:∠CFE与∠CBF互余,故④正确.
故选A.
6.A
【解】
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,设面积为S,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH,
即38+S=50-S,
解得S=6.
故选A.
7.C
【解】:∵∠ACB=90°,
∴EC⊥BC,
又∵BE平分∠ABC,DE⊥AB,
∴DE=CE,
又∵AC=12cm,
∴AE+DE=AE+CE=AC=12cm.
∴AE+DE+ADF=(AE+CE)+AD=AC+AD=12+8=20cm.
故选C.
8.C
解:①若OD平分∠BOE,则∠BOD=∠DOE,
∵∠COD=90°,
∴∠AOC+∠BOD=90°,∠AOC+∠DOE=90°,
又∵∠AOD+∠BOD=180°,∠AOD+∠DOE=180°,
∴∠AOC的余角和∠AOD的补角都有两个,
故①正确;
②若OC平分∠AOE,则∠AOC=∠EOC,
又∵∠COD=90°,
∴∠AOC+∠BOD=90°,∠COE+∠DOE=90°,
∴∠DOE=∠DOB,
∴OD平分∠BOE,
故②正确;
③若OE平分∠BOC,则OC平分∠AOE不一定成立,
故③错误;
④若OE平分∠BOC,则∠BOE=∠BOC=(180° ∠AOC)=90° ∠AOC,
又∵∠DOB=90° ∠AOC,
∴∠DOE=∠BOE ∠BOD=(90° ∠AOC) (90° ∠AOC)=∠AOC,
∴∠AOC=2∠DOE,
故④正确;故选:C.
9.C
解:如图示,连接,
,
是的平分线,
,①正确.
,②正确.
只是过点,并没有固定,明显③不成立.
故选:.
10.C
解:作GH⊥AB
由题意可知:BG是∠ABC的角平分线
又∵GH⊥AB,
∴CG=GH
∵
∴GH=2
由直线外一点到直线上各点的连线中,垂线段最短可得:
当点GP⊥AB时,有最小值
即= GH=2时,最短
故选:C
11.5
解:如图,过点D作DE⊥AB于点E,
∵,
∴AC⊥BC,
∵平分,
∴DE=CD=2,
∵,
∴的面积为 .
故答案为:5.
12.2
解:在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB DE+AC DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴×20DE+×8DF=10DE+4DF=14DE=28,
解得DE=2cm.
故答案为:2.
13.5
解:连接OA,过点O作OG⊥AB于G,OH⊥AC于H,
∵△ABC的周长是10,
∴AB+BC+AC=10,
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC,OG⊥AB,OH⊥AC,
∴OG=OH=OD=1,
∴△ABC的面积=△ABO的面积+△OBC的面积+△AOC的面积
=×AB×OG+×BC×OD+×AC×OH
=
=×10×1
=5,
故答案为:5.
14.①③④.
解:∵∠DAB=∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,∠ADB+∠ABD=90°,
∴∠DAC=∠BAE,
又AD=AB,AE=AC,
∴△DAC≌△BAE(SAS),
∴DC=BE,故①正确;
且∠ADC=∠ABE,
∴∠DFE=∠DBF+∠BDF=∠ABE+∠ABD+∠BDF=∠ABD+∠ADC+∠BDF=∠ABD+∠ADB=90°,
∴DC⊥BE,故③正确;
过A作AM⊥CD于M,AN⊥BE于N,
∴AM=AN,
∴FA平分∠DFE,故④正确;
无法通过已知条件和图形证明②正确,
故正确的结论是①③④,
故答案为:①③④.
15.2
解:如图,
由垂线段最短定理可知:当CE⊥OB时,CE 的长度最小,
∵点C在 ∠AOB 的平分线上,CD⊥OA,
∴CE=CD=2,
故答案为2 .
16.①②③④
解:①作PD⊥AC于D.
∵PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上,故①正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
在Rt△PAM和Rt△PAD中,
,
∴Rt△PAM≌Rt△PAD(HL),
∴∠APM=∠APD,
同理:Rt△PCD≌Rt△PCN(HL),
∴∠CPD=∠CPN,
∴∠MPN=2∠APC,
∴∠ABC+2∠APC=180°,②正确;
③∵PA平分∠CAE,BP平分∠ABC,
∴∠CAE=2∠PAM,
∵∠CAE=∠ABC+∠ACB,∠PAM=∠ABC+∠APB,
∴∠ACB=2∠APB,③正确;
④∵Rt△PAM≌Rt△PAD(已证),
∴AD=AM,
∵Rt△PCD≌Rt△PCN(已证),
∴CD=CN,
∴AM+CN=AD+CD=AC,④正确;
故答案为:①②③④.
17.见解析
解:如图,过点M作ME⊥AD于F,
∵∠C=90°,DM平分∠ADC,
∴ME=MC,
∵M是BC的中点,
∴BM=CM,
∴BM=EM,
又∵∠B=90°,
∴点M在∠BAD的平分线上,
∴AM平分∠DAB.
18.解析:欲证点P在的平分线上,只需证明点P到AC与CN的距离相等即可,可以分别作出点P到BM,AC,CN的垂线,结合题意证明即可.
答案:证明:如图,过点P作于点E,于点F,于点G,
∵点P为和的平分线的交点,
∴,,∴,
∴点P在的平分线上.
19.解:以为圆心,以任意长为半径作弧,交于两点,
再分别以点为圆心,以大于长为半径作弧,两弧在角的内部交于点,作射线,则为的角平分线,如下图:
(1)连接,如下图:
由作图可知:、、(公共边)
通过三角形三边相等求得
故答案为①
(2)在和中
∴
∴,即为的平分线
20.解:(1)∵AB∥CD
∴∠1=∠DCE=34°
∵CE平分∠ACD
∴∠ACE=∠DCE=34°
(2)∵CF⊥CE
∴∠FCE=90°
∴∠FCH=90°°=56°
∵∠2=56°
∴∠FCH=∠2
∴CF∥AG.
21解:证明:∵∠DEC+∠C=180°,∠F=∠1,
∴DEBC,ACDF,
∴∠ADE=∠B,∠EDF=∠BGD,∠C=∠BGD,
∴∠C=∠EDF,
∵DE平分∠ADF,
∴∠ADE=∠EDF,
∴∠B=∠C.
22.【解】
(1)∵中,,
∴,
又∵,,
∴;
(2)在延长线上标上点M,如图1所示.
∵,∴,.
∵平分,平分,
∴,,
∴,
∴.
(3)证明:如图2,由(2)知:,,
∵,
∴.
