2021-2022学年华东师大版数学八年级上册13.2.3 三角形全等的判定——边角边课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册13.2.3 三角形全等的判定——边角边课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 569.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 18:04:48 | ||
图片预览


文档简介
三角形全等的判定——边角边
一、单选题
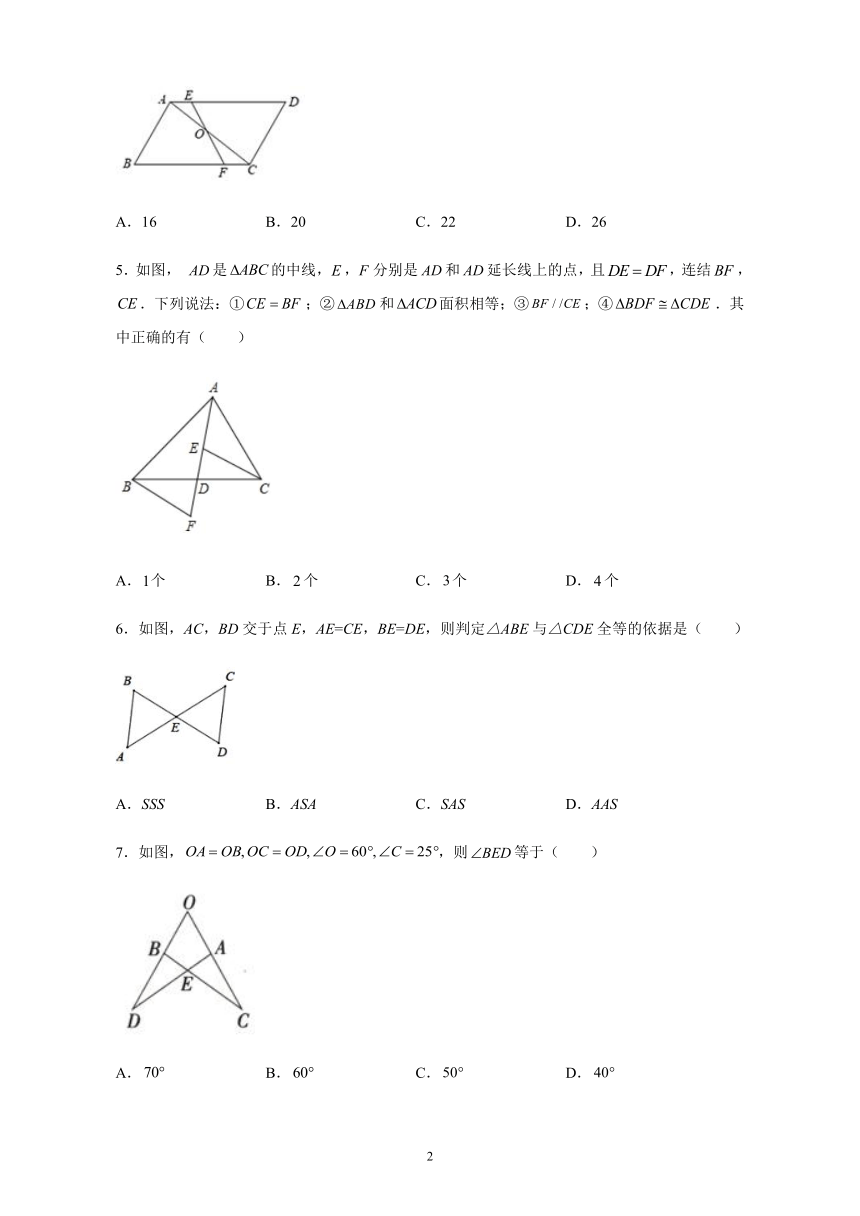
1.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=6厘米,圆形容器的壁厚是( )
A.厘米 B.6厘米 C.2厘米 D.5厘米
2.如图所示,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的是( )
A. B. C. D.
3.如图,已知方格纸中是4个相同的正方形,则与的和为( )
A. B. C. D.
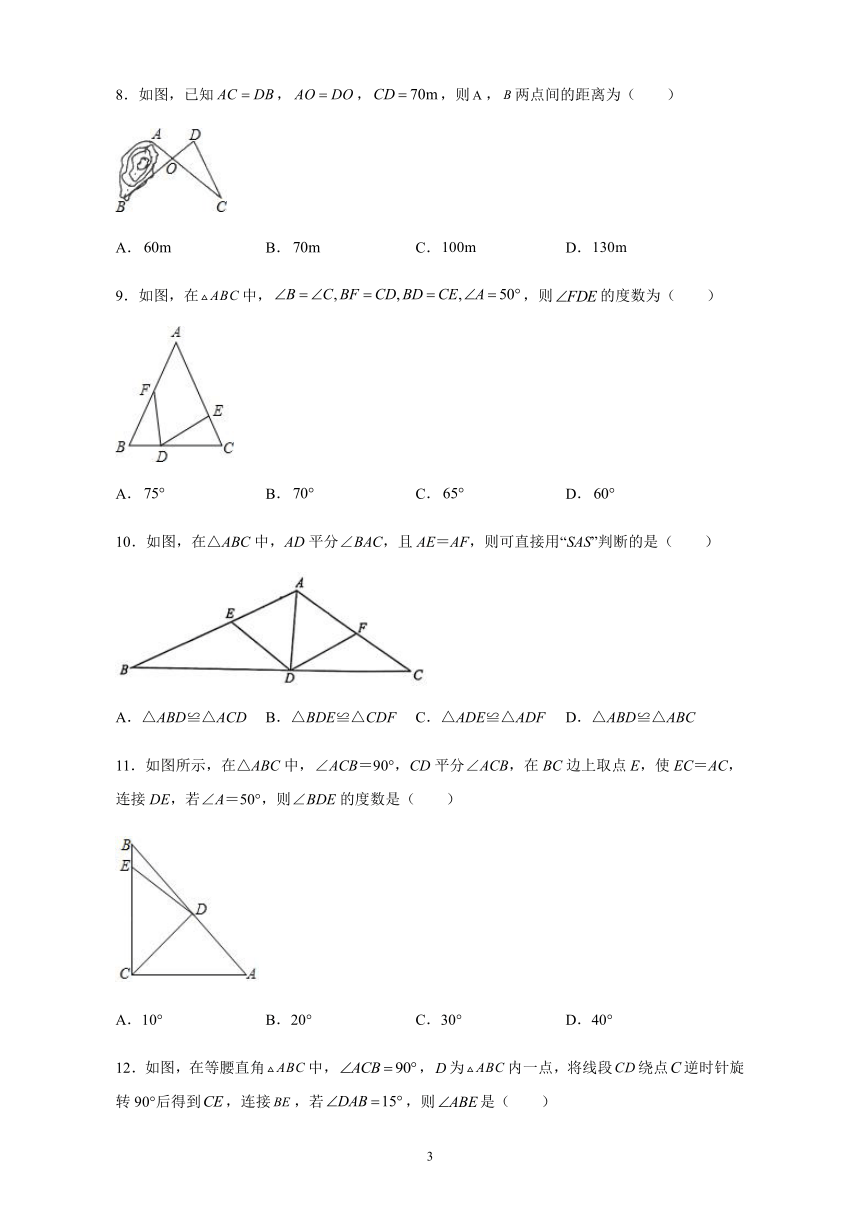
4.如图,四边形ABCD中,点E在AD上,点F在BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=CD=6,则四边形EFCD的周长是( )
A.16 B.20 C.22 D.26
5.如图, 是的中线,,分别是和延长线上的点,且,连结,.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.个 B.个 C.个 D.个
6.如图,AC,BD交于点E,AE=CE,BE=DE,则判定△ABE与△CDE全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
7.如图,,则等于( )
A. B. C. D.
8.如图,已知,,,则,两点间的距离为( )
A. B. C. D.
9.如图,在中,,则的度数为( )
A. B. C. D.
10.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD B.△BDE≌△CDF C.△ADE≌△ADF D.△ABD≌△ABC
11.如图所示,在△ABC中,∠ACB=90°,CD平分∠ACB,在BC边上取点E,使EC=AC,连接DE,若∠A=50°,则∠BDE的度数是( )
A.10° B.20° C.30° D.40°
12.如图,在等腰直角中,,为内一点,将线段绕点逆时针旋转90°后得到,连接,若,则是( )
A.75° B.78° C.80° D.92°
13.如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为( )
A.50° B.65° C.70° D.75°
14.如图,△ABC中,,,,则的度数是( )
A.65° B.70° C.75° D.60°
15.如图,,,,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动,设运动时间为,当与全等时,则点的运动速度为( ).
A. B.1 C.或 D.1或
二、填空题
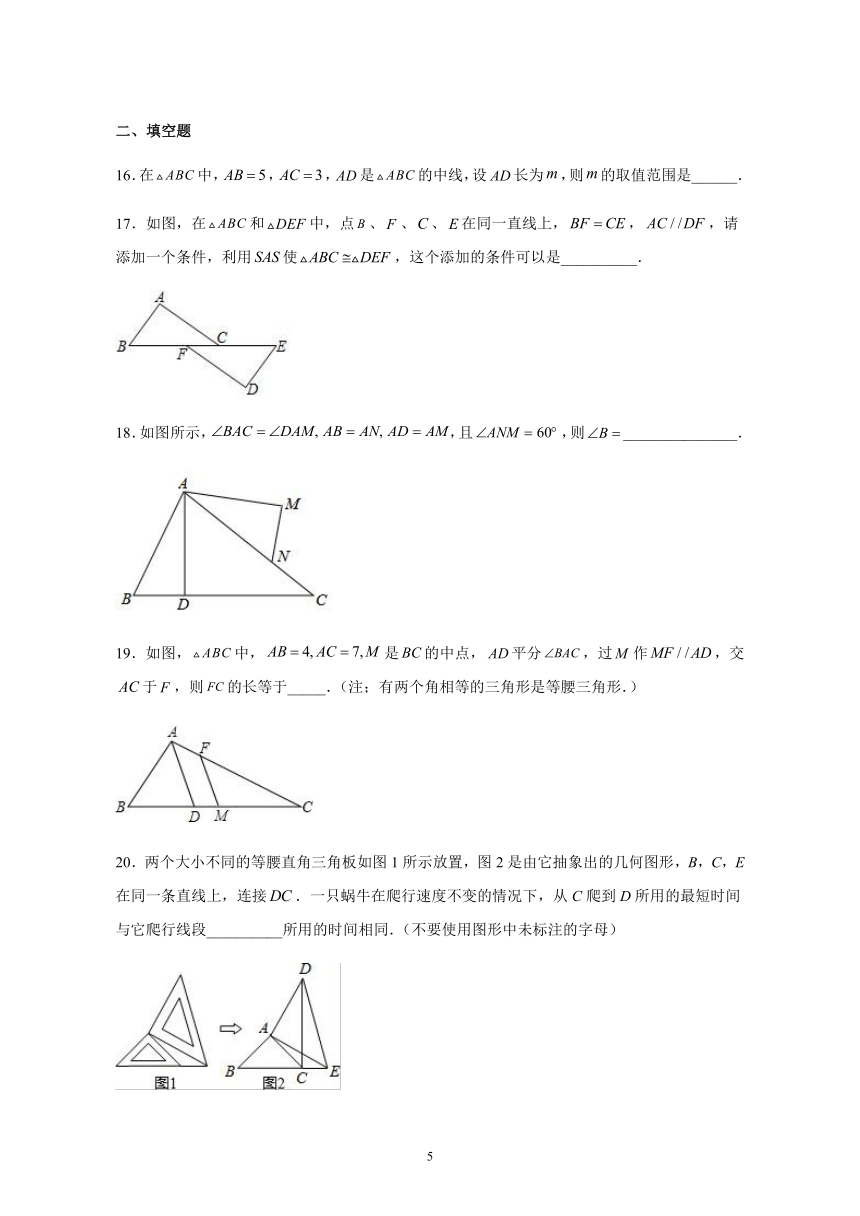
16.在中,,,是的中线,设长为,则的取值范围是______.
17.如图,在和中,点、、、在同一直线上,,,请添加一个条件,利用使,这个添加的条件可以是__________.
18.如图所示,,且,则_______________.
19.如图,中,是的中点,平分,过作,交于,则的长等于_____.(注;有两个角相等的三角形是等腰三角形.)
20.两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接.一只蜗牛在爬行速度不变的情况下,从C爬到D所用的最短时间与它爬行线段__________所用的时间相同.(不要使用图形中未标注的字母)
三、解答题
21.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,AB=DE,BF=CE,∠B=∠E,求证:△ABC≌△DEF.
22.如图,P为△ABC的外角平分线上任一点.求证:PB+PC≥AB+AC.
23.如图,在△ADC中,DB是高,点E是DB上一点,,,M、N分别是AE、CD上的点,且.
(1)△ABE和△DBC全等吗?请说明理由;
(2)探索BM与BN之间的数量关系和位置关系,并说明理由.
24.如图,四边形ABCD中,AB=BC=3厘米,DA=DC=4厘米,∠DAB=∠DCB=90°,点P从A点开始沿射线AB方向运动,点Q从点C开始沿射线BC方向运动,P、Q两点运动速度均为1厘米/秒,两点同时运动.
(1)在P、Q两点运动过程中,请问∠PDQ的大小是否发生变化?请说明理由;
(2)当点P在线段AB上运动时(如图1),请求出四边形PDQB的而积;
(3)如图2,P点运动到AB延长线上,设DP与线段BC的交点为E.
①当P、Q运动了多少秒时,S△CDE=S△BPE.
②当P、Q运动了多少秒时,第①小问中两个三角形的面积差为(3﹣)平方厘米.
参考答案
1.A
解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=5厘米,
∵EF=6厘米,
∴圆柱形容器的壁厚是(厘米),
故选:A.
2.D
解:∵AD=AE,
∴∠ADE=∠AED,
∵BD=CE,
∴BD+DE=CE+DE,即BE=CD,
∴△ABE≌△ACD(SAS),故选项A正确;
∵BD=CE,∠ADB=∠AEC=100°,AD=AE,
∴△ABD≌△ACE(SAS),故选项B正确;
∵∠BAE=70°,∠AEC=100°,
∴∠B=30°,
∵△ABE≌△ACD,
∴AB=AC,
∴∠B=∠C=30°,故选项C正确;
∵∠ADB=∠AEC=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=20°,故选项D错误;
故选:D.
3.C
解:
如图所示,在与中,
,
,
,
,
.
故选:C.
4.C
解:∵线段EF与AC交于点O且互相平分,
∴,.
∵,
∴,
∴AE=CF.
∵,
∴.
故选:C.
5.D
解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BFCE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的是①②③④.
故答案为:D.
6.C
解: AE=CE,,BE=DE,
(SAS).
故选C.
7.A
解:在△ODA和△OCB中
∴△ODA≌△OCB(SAS),
∴∠D=∠C=25°,
∵∠O=60°,∠C=25°,
∴∠DBE=60°+25°=85°,
∴∠BED=180° 85° 25°=70°,
故选:A.
8.B
解:∵AC=DB,AO=DO,
∴AC-AO=BD-OD,
即OB=OC,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=70m,
故选:B.
9.C
解:∵在△BFD和△CDE中,
,
∴△BFD≌△CDE(SAS),
∴∠BFD=∠CDE,
∵∠B=∠C,∠A=50°,
∴∠B=∠C=×(180°-∠A)=65°,
∴∠FDB+∠CDE=∠FDB+∠BFD=180°-∠B=115°,
∴∠FDE=180°-(∠FDB+∠EDC)=180°-115°=65°,
故选:C.
10.C
解:∵AD平分∠BAC,
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
故选:C.
11.A
解:∵∠ACB=90°,∠A=50°,
∴∠B=90°﹣∠A=40°,
∵CD平分∠ACB,
∴∠ECD=∠ACD,
在△CDE和△CDA中,
,
∴△CDE≌△CDA(SAS),
∴∠CED=∠A=50°,
又∵∠CED=∠B+∠BDE,
∴∠BDE=∠CED﹣∠B=50°﹣40°=10°,
故选:A.
12.A
解:∵△ABC是等腰直角三角形,
∴∠ABC=∠BAC=45°.
∴∠DAC=45°-15°=30°.
∵∠ACD+∠BCD=90°,∠ECB+∠BCD=90°
∴∠ECB=∠DCA
在△BEC和△ADC中,
,
∴△BCE≌△ACD(SAS).
∴∠EBC=∠DAC=30°.
∴∠ABE=∠EBC+∠ABC=75°.
故选:A.
13.B
解:
在和中
( SAS)
故选:B.
14.A
解:在和中,
,
∴≌,
∴,
∵,
∴,
∴,
故选:A.
15.D
解:设点Q的运动速度是x cm/s,
∵∠CAB=∠DBA,
∴△ACP与△BPQ全等,有两种情况:
①AP=BP,AC=BQ,
则,
解得:;
②AP=BQ,AC=BP,
则,
解得:
所以点的运动速度为或.
故选:D.
16.
解:如图,延长至 使
是的中线,
而
而,,长为,
则
故答案为:
17.
解:AC=DF,
理由是:∵BF=CE,
∴BF+FC=CE+CF,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
故答案为:AC=DF.
18.
解:∵,
∴,
∴,
在和中,
∴(SAS),
∴,
故答案为:.
19.5.5
解:如图,延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,
∵M是BC中点,
∴BM=CM,∠BMN=∠CMF,
∴△BMN≌△CMF,
∴BN=CF,∠N=∠MFC,
又∵∠BAD=∠CAD,MF∥AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC,
∴FC=(AB+AC)=5.5.
故答案为5.5.
20.
解:∵和是等腰直角三角形,
∴,
∴,
∴,
在和中,,
∴≌(SAS),
∴.
故答案为:BE.
21.见解析
解:∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
22.见解析
解:①如图,当点P与点A不重合时,在BA延长线上取一点D,使AD=AC,连接PD.
∵P为△ABC的外角平分线上一点,
∴∠1=∠2 ,
∵在△PAD和△PAC中
∴△PAD≌△PAC(SAS),
∴PD=PC,
在△PBD中,PB+PD>BD,
BD=AB+AD,
∴PB+PC>AB+AC.
②当点P与点A重合时,PB+PC=AB+AC.
综上,PB+PC≥AB+AC.
23.(1)△ABE和△DBC全等,理由见解析;(2)BM=BN,BM⊥BN;理由见解析.
解:(1)△ABE≌△DBC;理由是:
∵DB是高,
∴∠ABE=∠DBC=90°.
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS).
(2)BM=BN,MB⊥BN;理由是:
∵△ABE≌△DBC,
∴∠BAM=∠BDN.
在△ABM 和△DBN 中,
∴△ABM≌△DBN(SAS).
∴BM=BN,∠ABM=∠DBN.
∵∠ABM+∠DBM=∠ABD=90°.
∴∠DBN+∠DBM =90°.
即∠MBN=90°.
∴BM⊥BN.
24.(1)∠PDQ的大小不发生变化,总等于∠ADC;(2)四边形PDQB的而积为12平方厘米;(3)①P、Q运动了6秒时,S△CDE=S△BPE;②当秒或秒时,S△BPE与S△CDE的差为(3﹣)平方厘米.
解:(1)∠PDQ的大小不发生变化,
理由是:∵∠A=∠DCB=∠DCQ=90°,由已知得出AP=CQ,
∴在△DAP和△DCQ中,
,
∴△DAP≌△DCQ(SAS),
∴∠ADP=∠CDQ,
∴∠PDQ=∠PDC+∠CDQ=∠PDC+∠ADP=∠ADC,
即∠PDQ的大小不发生变化,总等于∠ADC;
(2)∵△ADP≌△DCQ,
∴S△ADP=S△DCQ,
∴四边形PDQB的面积是:
S四边形PDQB=S四边形PDCB+S△CDQ
=S四边形PDCB+S△ADP
=S四边形ABCD
=×3×4+×3×4
=12(平方厘米);
(2)①连接BD,
设P、Q运动了t秒时,S△CDE=S△BPE,
∵S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB=0,
∵AB=BC=3,AP=t,DA=DC=4,
×3×4-×(t-3)×4=0,
解得t=6,
即P、Q运动了6秒时,S△CDE=S△BPE;
②连接BD,
设P、Q运动了t秒时,S△CDE-S△BPE=3-(平方厘米),
∴AP=CQ=t,
∴S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB,或S△BPE-S△CDE=S△PDB-S△DCB,
∵AB=BC=3,AP=t,DA=DC=4,
∴S△DCB=×3×4=6,S△PDB=×(t-3)×4=2(t-3),
∴S△CDE-S△BPE=S△DCB-S△PDB=6-2(t-3)=3-.
解得(秒),
或S△BPE-S△CDE=S△PDB-S△DCB=2(t-3)-6=3-.
解得(秒),
综上,当秒或秒时,S△BPE与S△CDE的差为(3﹣)平方厘米.
一、单选题
1.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=6厘米,圆形容器的壁厚是( )
A.厘米 B.6厘米 C.2厘米 D.5厘米
2.如图所示,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的是( )
A. B. C. D.
3.如图,已知方格纸中是4个相同的正方形,则与的和为( )
A. B. C. D.
4.如图,四边形ABCD中,点E在AD上,点F在BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=CD=6,则四边形EFCD的周长是( )
A.16 B.20 C.22 D.26
5.如图, 是的中线,,分别是和延长线上的点,且,连结,.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.个 B.个 C.个 D.个
6.如图,AC,BD交于点E,AE=CE,BE=DE,则判定△ABE与△CDE全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
7.如图,,则等于( )
A. B. C. D.
8.如图,已知,,,则,两点间的距离为( )
A. B. C. D.
9.如图,在中,,则的度数为( )
A. B. C. D.
10.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD B.△BDE≌△CDF C.△ADE≌△ADF D.△ABD≌△ABC
11.如图所示,在△ABC中,∠ACB=90°,CD平分∠ACB,在BC边上取点E,使EC=AC,连接DE,若∠A=50°,则∠BDE的度数是( )
A.10° B.20° C.30° D.40°
12.如图,在等腰直角中,,为内一点,将线段绕点逆时针旋转90°后得到,连接,若,则是( )
A.75° B.78° C.80° D.92°
13.如图,△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,D,E在同一条直线上,若∠CAE+∠ACE+∠ADE=130°,则∠ADE的度数为( )
A.50° B.65° C.70° D.75°
14.如图,△ABC中,,,,则的度数是( )
A.65° B.70° C.75° D.60°
15.如图,,,,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动,设运动时间为,当与全等时,则点的运动速度为( ).
A. B.1 C.或 D.1或
二、填空题
16.在中,,,是的中线,设长为,则的取值范围是______.
17.如图,在和中,点、、、在同一直线上,,,请添加一个条件,利用使,这个添加的条件可以是__________.
18.如图所示,,且,则_______________.
19.如图,中,是的中点,平分,过作,交于,则的长等于_____.(注;有两个角相等的三角形是等腰三角形.)
20.两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接.一只蜗牛在爬行速度不变的情况下,从C爬到D所用的最短时间与它爬行线段__________所用的时间相同.(不要使用图形中未标注的字母)
三、解答题
21.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,AB=DE,BF=CE,∠B=∠E,求证:△ABC≌△DEF.
22.如图,P为△ABC的外角平分线上任一点.求证:PB+PC≥AB+AC.
23.如图,在△ADC中,DB是高,点E是DB上一点,,,M、N分别是AE、CD上的点,且.
(1)△ABE和△DBC全等吗?请说明理由;
(2)探索BM与BN之间的数量关系和位置关系,并说明理由.
24.如图,四边形ABCD中,AB=BC=3厘米,DA=DC=4厘米,∠DAB=∠DCB=90°,点P从A点开始沿射线AB方向运动,点Q从点C开始沿射线BC方向运动,P、Q两点运动速度均为1厘米/秒,两点同时运动.
(1)在P、Q两点运动过程中,请问∠PDQ的大小是否发生变化?请说明理由;
(2)当点P在线段AB上运动时(如图1),请求出四边形PDQB的而积;
(3)如图2,P点运动到AB延长线上,设DP与线段BC的交点为E.
①当P、Q运动了多少秒时,S△CDE=S△BPE.
②当P、Q运动了多少秒时,第①小问中两个三角形的面积差为(3﹣)平方厘米.
参考答案
1.A
解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=5厘米,
∵EF=6厘米,
∴圆柱形容器的壁厚是(厘米),
故选:A.
2.D
解:∵AD=AE,
∴∠ADE=∠AED,
∵BD=CE,
∴BD+DE=CE+DE,即BE=CD,
∴△ABE≌△ACD(SAS),故选项A正确;
∵BD=CE,∠ADB=∠AEC=100°,AD=AE,
∴△ABD≌△ACE(SAS),故选项B正确;
∵∠BAE=70°,∠AEC=100°,
∴∠B=30°,
∵△ABE≌△ACD,
∴AB=AC,
∴∠B=∠C=30°,故选项C正确;
∵∠ADB=∠AEC=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=20°,故选项D错误;
故选:D.
3.C
解:
如图所示,在与中,
,
,
,
,
.
故选:C.
4.C
解:∵线段EF与AC交于点O且互相平分,
∴,.
∵,
∴,
∴AE=CF.
∵,
∴.
故选:C.
5.D
解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BFCE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的是①②③④.
故答案为:D.
6.C
解: AE=CE,,BE=DE,
(SAS).
故选C.
7.A
解:在△ODA和△OCB中
∴△ODA≌△OCB(SAS),
∴∠D=∠C=25°,
∵∠O=60°,∠C=25°,
∴∠DBE=60°+25°=85°,
∴∠BED=180° 85° 25°=70°,
故选:A.
8.B
解:∵AC=DB,AO=DO,
∴AC-AO=BD-OD,
即OB=OC,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=70m,
故选:B.
9.C
解:∵在△BFD和△CDE中,
,
∴△BFD≌△CDE(SAS),
∴∠BFD=∠CDE,
∵∠B=∠C,∠A=50°,
∴∠B=∠C=×(180°-∠A)=65°,
∴∠FDB+∠CDE=∠FDB+∠BFD=180°-∠B=115°,
∴∠FDE=180°-(∠FDB+∠EDC)=180°-115°=65°,
故选:C.
10.C
解:∵AD平分∠BAC,
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
故选:C.
11.A
解:∵∠ACB=90°,∠A=50°,
∴∠B=90°﹣∠A=40°,
∵CD平分∠ACB,
∴∠ECD=∠ACD,
在△CDE和△CDA中,
,
∴△CDE≌△CDA(SAS),
∴∠CED=∠A=50°,
又∵∠CED=∠B+∠BDE,
∴∠BDE=∠CED﹣∠B=50°﹣40°=10°,
故选:A.
12.A
解:∵△ABC是等腰直角三角形,
∴∠ABC=∠BAC=45°.
∴∠DAC=45°-15°=30°.
∵∠ACD+∠BCD=90°,∠ECB+∠BCD=90°
∴∠ECB=∠DCA
在△BEC和△ADC中,
,
∴△BCE≌△ACD(SAS).
∴∠EBC=∠DAC=30°.
∴∠ABE=∠EBC+∠ABC=75°.
故选:A.
13.B
解:
在和中
( SAS)
故选:B.
14.A
解:在和中,
,
∴≌,
∴,
∵,
∴,
∴,
故选:A.
15.D
解:设点Q的运动速度是x cm/s,
∵∠CAB=∠DBA,
∴△ACP与△BPQ全等,有两种情况:
①AP=BP,AC=BQ,
则,
解得:;
②AP=BQ,AC=BP,
则,
解得:
所以点的运动速度为或.
故选:D.
16.
解:如图,延长至 使
是的中线,
而
而,,长为,
则
故答案为:
17.
解:AC=DF,
理由是:∵BF=CE,
∴BF+FC=CE+CF,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
故答案为:AC=DF.
18.
解:∵,
∴,
∴,
在和中,
∴(SAS),
∴,
故答案为:.
19.5.5
解:如图,延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,
∵M是BC中点,
∴BM=CM,∠BMN=∠CMF,
∴△BMN≌△CMF,
∴BN=CF,∠N=∠MFC,
又∵∠BAD=∠CAD,MF∥AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC,
∴FC=(AB+AC)=5.5.
故答案为5.5.
20.
解:∵和是等腰直角三角形,
∴,
∴,
∴,
在和中,,
∴≌(SAS),
∴.
故答案为:BE.
21.见解析
解:∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
22.见解析
解:①如图,当点P与点A不重合时,在BA延长线上取一点D,使AD=AC,连接PD.
∵P为△ABC的外角平分线上一点,
∴∠1=∠2 ,
∵在△PAD和△PAC中
∴△PAD≌△PAC(SAS),
∴PD=PC,
在△PBD中,PB+PD>BD,
BD=AB+AD,
∴PB+PC>AB+AC.
②当点P与点A重合时,PB+PC=AB+AC.
综上,PB+PC≥AB+AC.
23.(1)△ABE和△DBC全等,理由见解析;(2)BM=BN,BM⊥BN;理由见解析.
解:(1)△ABE≌△DBC;理由是:
∵DB是高,
∴∠ABE=∠DBC=90°.
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS).
(2)BM=BN,MB⊥BN;理由是:
∵△ABE≌△DBC,
∴∠BAM=∠BDN.
在△ABM 和△DBN 中,
∴△ABM≌△DBN(SAS).
∴BM=BN,∠ABM=∠DBN.
∵∠ABM+∠DBM=∠ABD=90°.
∴∠DBN+∠DBM =90°.
即∠MBN=90°.
∴BM⊥BN.
24.(1)∠PDQ的大小不发生变化,总等于∠ADC;(2)四边形PDQB的而积为12平方厘米;(3)①P、Q运动了6秒时,S△CDE=S△BPE;②当秒或秒时,S△BPE与S△CDE的差为(3﹣)平方厘米.
解:(1)∠PDQ的大小不发生变化,
理由是:∵∠A=∠DCB=∠DCQ=90°,由已知得出AP=CQ,
∴在△DAP和△DCQ中,
,
∴△DAP≌△DCQ(SAS),
∴∠ADP=∠CDQ,
∴∠PDQ=∠PDC+∠CDQ=∠PDC+∠ADP=∠ADC,
即∠PDQ的大小不发生变化,总等于∠ADC;
(2)∵△ADP≌△DCQ,
∴S△ADP=S△DCQ,
∴四边形PDQB的面积是:
S四边形PDQB=S四边形PDCB+S△CDQ
=S四边形PDCB+S△ADP
=S四边形ABCD
=×3×4+×3×4
=12(平方厘米);
(2)①连接BD,
设P、Q运动了t秒时,S△CDE=S△BPE,
∵S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB=0,
∵AB=BC=3,AP=t,DA=DC=4,
×3×4-×(t-3)×4=0,
解得t=6,
即P、Q运动了6秒时,S△CDE=S△BPE;
②连接BD,
设P、Q运动了t秒时,S△CDE-S△BPE=3-(平方厘米),
∴AP=CQ=t,
∴S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB,或S△BPE-S△CDE=S△PDB-S△DCB,
∵AB=BC=3,AP=t,DA=DC=4,
∴S△DCB=×3×4=6,S△PDB=×(t-3)×4=2(t-3),
∴S△CDE-S△BPE=S△DCB-S△PDB=6-2(t-3)=3-.
解得(秒),
或S△BPE-S△CDE=S△PDB-S△DCB=2(t-3)-6=3-.
解得(秒),
综上,当秒或秒时,S△BPE与S△CDE的差为(3﹣)平方厘米.
