2021-2022学年华东师大版八年级数学上册13.2.4三角形全等的判定——角边角课时练习(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册13.2.4三角形全等的判定——角边角课时练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 612.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 18:08:25 | ||
图片预览

文档简介
三角形全等的判定——角边角
一、单选题
1.如图,要测量河两岸相对的两点、间的距离,先在垂直于的河岸上作出线段,并在延长线上取一点,使,再过点作垂线段,使点,,在一条直线上,则可判断的理由是
A. B. C. D.
2.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ).
A.带①去 B.带②去 C.带③去 D.①②③都带
3.如图,已知0A=OB,OC=OD,下列结论中:①∠A=∠B;②DE=CE;③连OE,则OE平分∠O,正确的是( )
A.①② B.②③ C.①③ D.①②③
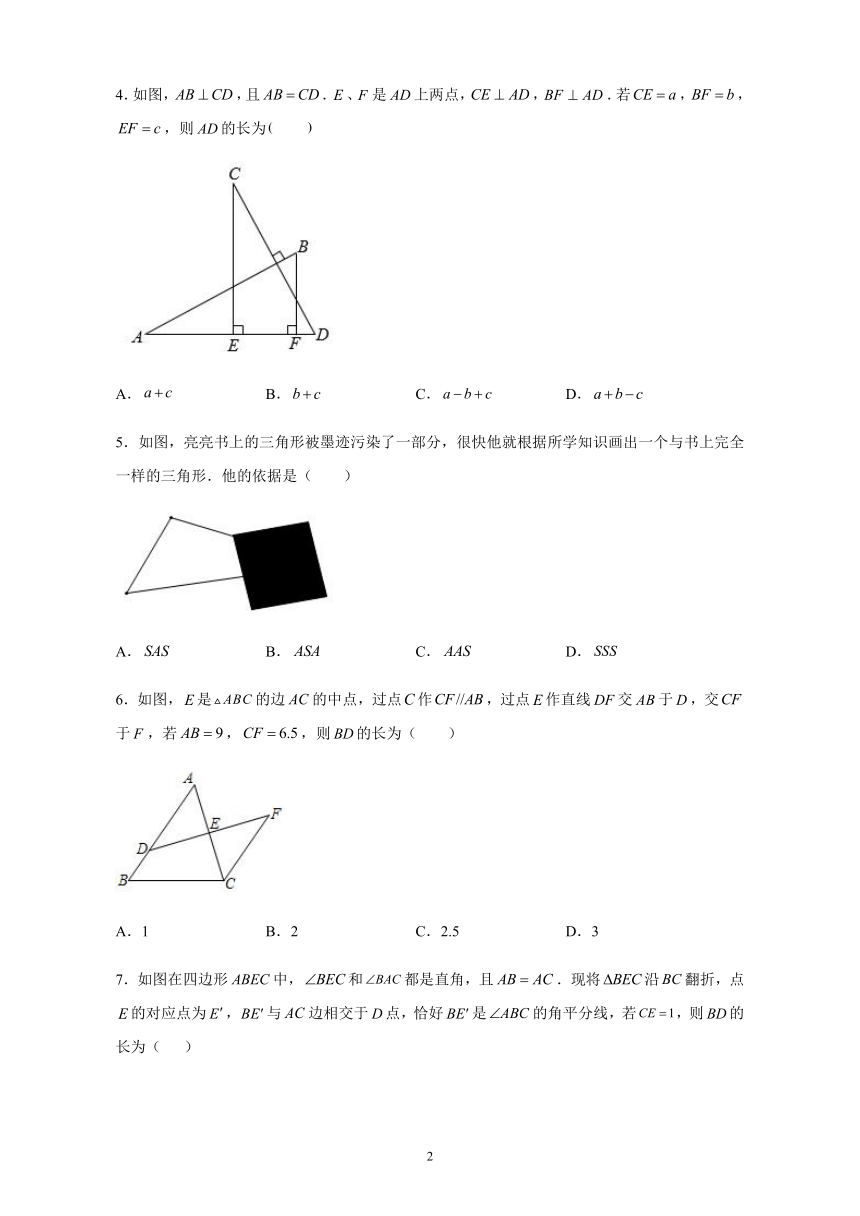
4.如图,,且.、是上两点,,.若,,,则的长为
A. B. C. D.
5.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A. B. C. D.
6.如图,是的边的中点,过点作,过点作直线交于,交于,若,,则的长为( )
A.1 B.2 C.2.5 D.3
7.如图在四边形中,和都是直角,且.现将沿翻折,点的对应点为,与边相交于点,恰好是的角平分线,若,则的长为( )
A.1.5 B.1.6 C.2 D.3
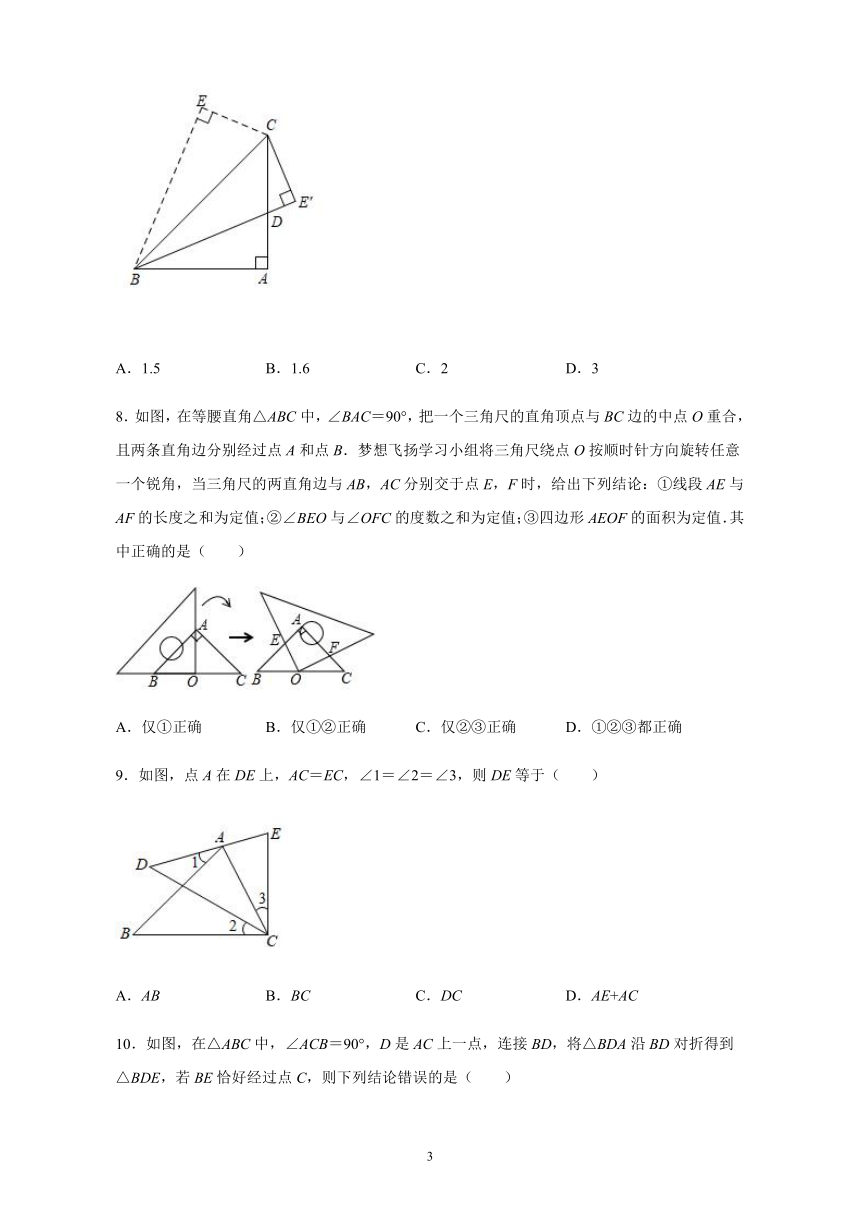
8.如图,在等腰直角△ABC中,∠BAC=90°,把一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B.梦想飞扬学习小组将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,给出下列结论:①线段AE与AF的长度之和为定值;②∠BEO与∠OFC的度数之和为定值;③四边形AEOF的面积为定值.其中正确的是( )
A.仅①正确 B.仅①②正确 C.仅②③正确 D.①②③都正确
9.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB B.BC C.DC D.AE+AC
10.如图,在△ABC中,∠ACB=90°,D是AC上一点,连接BD,将△BDA沿BD对折得到△BDE,若BE恰好经过点C,则下列结论错误的是( )
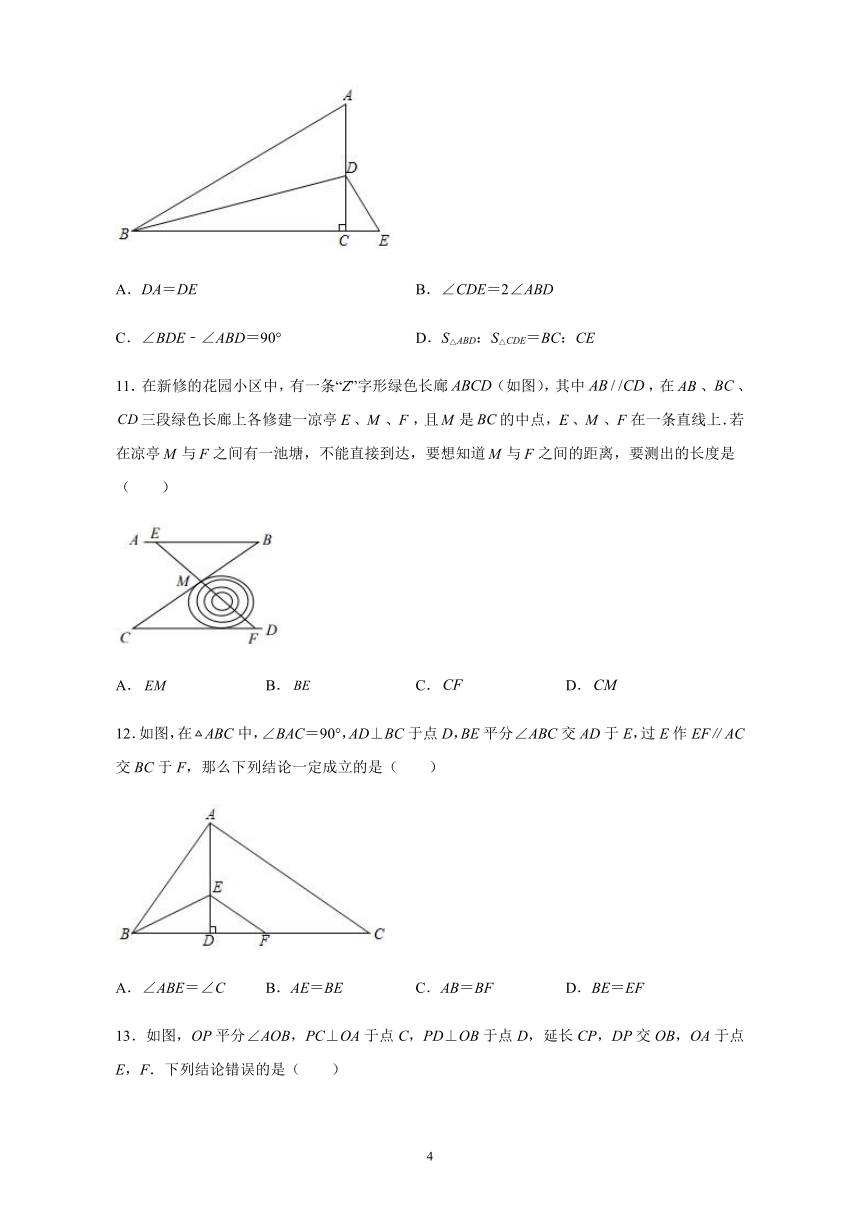
A.DA=DE B.∠CDE=2∠ABD
C.∠BDE﹣∠ABD=90° D.S△ABD:S△CDE=BC:CE
11.在新修的花园小区中,有一条“Z”字形绿色长廊(如图),其中,在、、三段绿色长廊上各修建一凉亭、、,且是的中点,、、在一条直线上.若在凉亭与之间有一池塘,不能直接到达,要想知道与之间的距离,要测出的长度是( )
A. B. C. D.
12.如图,在ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC交AD于E,过E作EF∥AC交BC于F,那么下列结论一定成立的是( )
A.∠ABE=∠C B.AE=BE C.AB=BF D.BE=EF
13.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,延长CP,DP交OB,OA于点E,F.下列结论错误的是( )
A.PC=PD B.OC=OD C.∠CPO=∠DPO D.PC=PE
二、填空题
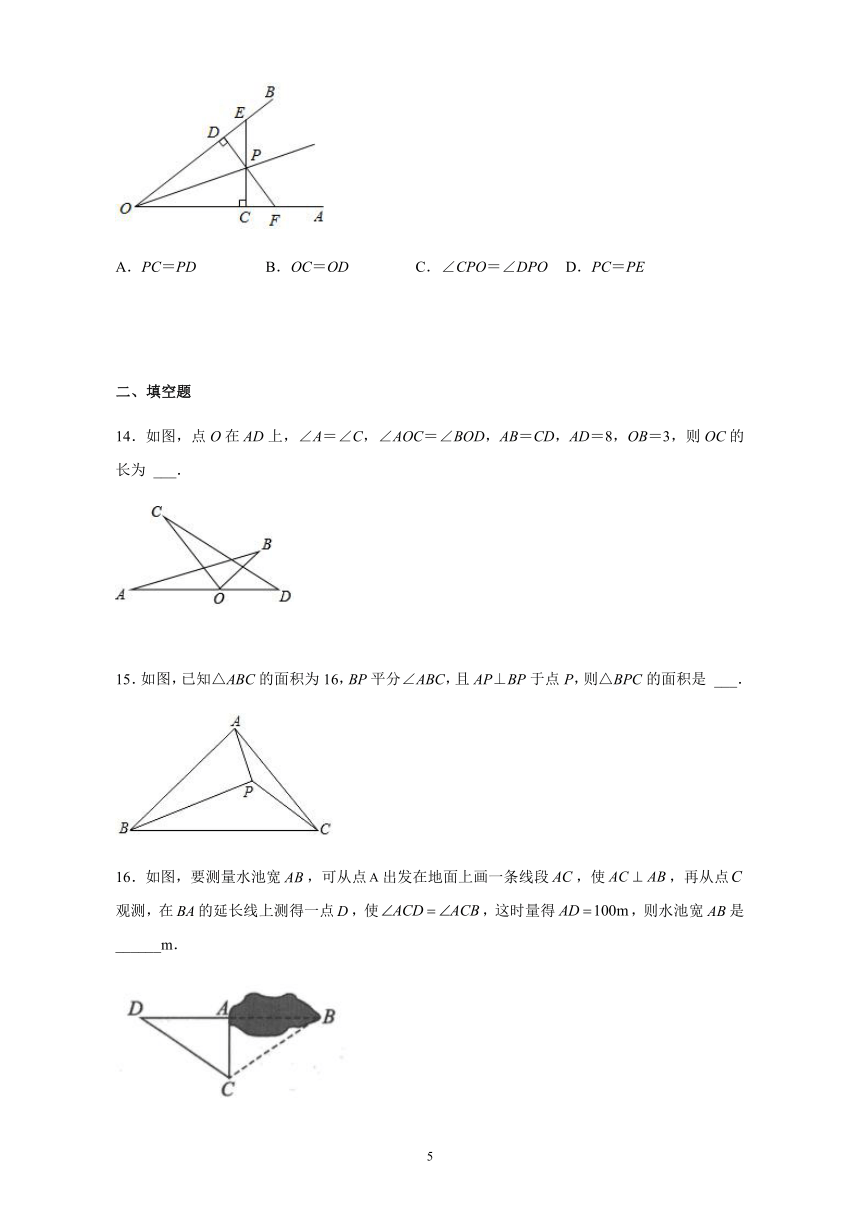
14.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=8,OB=3,则OC的长为 ___.
15.如图,已知△ABC的面积为16,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是 ___.
16.如图,要测量水池宽,可从点出发在地面上画一条线段,使,再从点观测,在的延长线上测得一点,使,这时量得,则水池宽是______m.
17.如图,平面直角坐标系中,C(0,4),A(1,0),K为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点K在x轴上运动时,BK的最小值为 ________.
18.如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以lcm/s的速度运动,P、Q两点同吋出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).连接PQ,当线段PQ经过点C时,t的值为______.
三、解答题
19.已知:如图,点B,D在线段AE上,AB=ED,AC∥EH,∠C=∠H.求证:BC=DH.
20.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AE=AD.
21.如图,小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一颗树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约0.5米,估计小刚在点A处时他与电线塔的距离,并说明理由.
22.如图,AB∥FC,E是DF的中点.
(1)求证:△ADE≌△CFE;
(2)若AB=10,CF=6,求BD的长.
23.综合与实践
如图1所示,已知△ABC中,∠ACB=90°,AC=BC,直线m经过点C,过A、B两点分别作直线m的垂线,垂足分别为E、F.
(1)如图1,当直线m在A、B两点同侧时,直接写出EF与AE、BF之间的数量关系;
(2)若直线m绕点C旋转到图2所示的位置时(BF<AE),其余条件不变,猜想EF与AE,BF有什么数量关系?并证明你的猜想;
(3)若直线m绕点C旋转到图3所示的位置时(BF>AE)其余条件不变,问EF与AE,BF的数量关系如何?直接写出猜想结论,不需证明.
参考答案
1.D
解:,,
.
在与中,
.
故选:D.
2.C
解:带③去,理由如下:
∵③中满足ASA的条件,
∴带③去,
故选C.
3.D
解:,,为公共角,
,
,故①符合题意;
,即,且,(对顶角相等),
,
,故②符合题意,
∴;
连接,
,,为公共边,
,
,即平分,③符合题意.
综上得①②③均正确.
故选:D.
4.D
解:∵,,,
∴,,,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
故选:D.
5.B
解:被墨迹污染的三角形,已知两个角与这两个角所夹的边,故由ASA即可画出三角形,其依据是ASA.
故选:B.
6.C
解:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中,
∠1=∠F,∠A=∠2,AE=EC,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB AD=9 6.5=2.5,
故选:C.
7.C
解:如图,延长CE′和BA相交于点F,
由翻折可知:
∠BE'C=∠E=90°,CE'=CE=1,
∵BE'是∠ABC的角平分线,
∴∠CBE'=∠FBE',
∵BE′=BE′,
∴△BE'C △BE'F(ASA),
∴E'F=CE'=1,
∴CF=2,
∵∠FCA+∠F=90°,∠DBA+∠F=90°,
∴∠FCA=∠DBA,
∵∠FAC=∠DAB=90°,AB=AC,
∴△FCA △DBA(ASA),
∴BD=CF=2.
故选:C.
8.D
解:连接,如图所示,
为等腰直角三角形,点为的中点,
,,.
,,
.
在和中,
,
,
,
,
则结论①正确;
,,,
,
则结论②正确;
,
,
,
则结论③正确.
故选:.
9.A
解:设AB、DC相交于点O,
∵∠1=∠2,,
∴,
∴∠B=∠D,
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(AAS),
∴AB=ED.
故选:A.
10.D
解:如图,延长ED交AB于点F,
∵△BDA沿BD对折得到△BDE,
∴△BDA≌△BDE,
∴∠ABD=∠DBE,DA=DE,
故A正确,不符合题意;
由△BDA≌△BDE可知,
∠A=∠E,AB=BE,
在△ABC和△EBF中,
,
∴△ABC≌△EBF(ASA),
∴BC=BF,
在△FBD和△CBD中,
,
∴△FBD≌△CBD(SAS),
∴∠DCB=∠DFB=90°,DF=DC,
∴∠ABC=∠CDE,
∴∠CDE=2∠ABD,
故B正确,不符合题意;
∵∠BDE=∠BDC+∠CDE=∠BDC+2∠ABD,
∴∠BDE﹣∠ABD
=∠BDC+2∠ABD﹣∠ABD
=∠BDC+∠ABD
=∠BDC+∠DBC
=90°,
故C正确,不符合题意;
S△ABD= AB DF,S△CDE= CE CD,
∴==,
故D错误,符合题意;
故选:D.
11.A
解:∵AB∥CD
∴∠B=∠C,∠BEM=∠CFM
∵M是BC的中点
∴BM=CM
∴△EMB≌△FMC(AAS)
∴EM=FM
∴只需要测量出EM的长度即可
故选A.
12.C
解:∵AD⊥BC,
∴∠ADC=90°,
∴∠C+∠DAC=90°,
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∴∠C=∠BAD,
∵EF//AC,
∴∠C=∠BFE,
∴∠BAD=∠BFE,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE和△FBE中,
,
∴△ABE≌△FBE(AAS),
∴AB=BF,
故选:C.
13.D
解:∵OP平分∠AOB,
∴∠POD=∠POC,
∵PD⊥OB,PC⊥OA,
∴∠PCO=∠PDO,
在△POD和△POC中,
,
∴△POC≌△POD(AAS),
∴PC=PD,OC=OD,∠CPO=∠DPO,故A,B,C正确;
故选:D.
14.5
解:∵∠AOC=∠D+∠C,∠BOD=∠A+∠B,∠A=∠C,∠AOC=∠BOD,
∴∠B=∠D,
在△AOB和△COD中,
∵,
∴△AOB≌△COD,
∴OA=OC,DO=OB,
∴OC=OA=AD-OD= AD-OB =8-3=5,
∴OC的长为5
故答案为:5
15.8
解:
如图所示,延长AP交BC于D,
BP平分∠ABC,
,
,
,
在和中,
,
,
,
,,
,
故答案为:8.
16.
解:,
,
,,
,
,
故答案为:100
17.1
解:根据点到直线的距离可知,当轴时,最小,如下图:
则,,
∴
∴
∴
∴
故答案为1
18.1或2或1
解:在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤时,3t=4-t,
解得:t=1;
当<t≤时,8-3t=4-t,
解得:t=2;
综上所述,当线段PQ经过点C时,t的值为1s或2s.
.
19.证明见详解.
解: ∵AC∥EH,
∴∠A=∠E,
在△ABC和△EDH中
,
∴△ABC≌△EDH(AAS),
∴BC=DH.
20.证明见解析
解:∵AB=AC,∠B=∠C
∴
∴(ASA)
∴.
21.(1)答案见解析;(2)40米
解:(1)根据题意可知步,步.
故可画示意图如下:
(2)根据题意可知:,
∴在和中 ,
∴,
∴AB=ED=80步
小刚一步大约0.5米,
∴小刚在点A处时他与电线塔的距离为米.
22.(1)见解析;(2)4
解:(1)∵,
∴,
∵是的中点,
∴,
在和中,
,
∴,
(2)∵,
∴,
∴.
23.(1)EF=AE+BF;(2)EF=AE﹣BF,证明见解析;(3)EF=BF﹣AE
解:(1)EF=AE+BF;
证明如下:∵
∴
由题意得:,
∴,
∴
在和中
∴
∴、
又∵
∴
(2)EF=AE﹣BF
∵∠ACB=90°,
∴∠ACE+∠FCB=90°,
又∵AE⊥m,BF⊥m,
∴∠AEC=90°,∠BFC=90°,
∴∠CAE+∠ACE=90°,
∴∠CAE=∠FCB,
又∵AC=BC,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CF﹣CE=AE﹣BF;
(3)EF=BF﹣AE
∵∠ACB=90°,
∴∠ACE+∠FCB=90°,
又∵AE⊥m,BF⊥m,
∴∠AEC=90°,∠BFC=90°,
∴∠CAE+∠ACE=90°,
∴∠CAE=∠FCB,
又∵AC=BC,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CE﹣CF=BF﹣AE;
一、单选题
1.如图,要测量河两岸相对的两点、间的距离,先在垂直于的河岸上作出线段,并在延长线上取一点,使,再过点作垂线段,使点,,在一条直线上,则可判断的理由是
A. B. C. D.
2.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ).
A.带①去 B.带②去 C.带③去 D.①②③都带
3.如图,已知0A=OB,OC=OD,下列结论中:①∠A=∠B;②DE=CE;③连OE,则OE平分∠O,正确的是( )
A.①② B.②③ C.①③ D.①②③
4.如图,,且.、是上两点,,.若,,,则的长为
A. B. C. D.
5.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A. B. C. D.
6.如图,是的边的中点,过点作,过点作直线交于,交于,若,,则的长为( )
A.1 B.2 C.2.5 D.3
7.如图在四边形中,和都是直角,且.现将沿翻折,点的对应点为,与边相交于点,恰好是的角平分线,若,则的长为( )
A.1.5 B.1.6 C.2 D.3
8.如图,在等腰直角△ABC中,∠BAC=90°,把一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B.梦想飞扬学习小组将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,给出下列结论:①线段AE与AF的长度之和为定值;②∠BEO与∠OFC的度数之和为定值;③四边形AEOF的面积为定值.其中正确的是( )
A.仅①正确 B.仅①②正确 C.仅②③正确 D.①②③都正确
9.如图,点A在DE上,AC=EC,∠1=∠2=∠3,则DE等于( )
A.AB B.BC C.DC D.AE+AC
10.如图,在△ABC中,∠ACB=90°,D是AC上一点,连接BD,将△BDA沿BD对折得到△BDE,若BE恰好经过点C,则下列结论错误的是( )
A.DA=DE B.∠CDE=2∠ABD
C.∠BDE﹣∠ABD=90° D.S△ABD:S△CDE=BC:CE
11.在新修的花园小区中,有一条“Z”字形绿色长廊(如图),其中,在、、三段绿色长廊上各修建一凉亭、、,且是的中点,、、在一条直线上.若在凉亭与之间有一池塘,不能直接到达,要想知道与之间的距离,要测出的长度是( )
A. B. C. D.
12.如图,在ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC交AD于E,过E作EF∥AC交BC于F,那么下列结论一定成立的是( )
A.∠ABE=∠C B.AE=BE C.AB=BF D.BE=EF
13.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,延长CP,DP交OB,OA于点E,F.下列结论错误的是( )
A.PC=PD B.OC=OD C.∠CPO=∠DPO D.PC=PE
二、填空题
14.如图,点O在AD上,∠A=∠C,∠AOC=∠BOD,AB=CD,AD=8,OB=3,则OC的长为 ___.
15.如图,已知△ABC的面积为16,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是 ___.
16.如图,要测量水池宽,可从点出发在地面上画一条线段,使,再从点观测,在的延长线上测得一点,使,这时量得,则水池宽是______m.
17.如图,平面直角坐标系中,C(0,4),A(1,0),K为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点K在x轴上运动时,BK的最小值为 ________.
18.如图,AE与BD相交于点C,AC=EC,BC=DC,AB=4cm,点P从点A出发,沿A→B→A方向以3cm/s的速度运动,点Q从点D出发,沿D→E方向以lcm/s的速度运动,P、Q两点同吋出发.当点P到达点A时,P、Q两点同时停止运动.设点P的运动时间为t(s).连接PQ,当线段PQ经过点C时,t的值为______.
三、解答题
19.已知:如图,点B,D在线段AE上,AB=ED,AC∥EH,∠C=∠H.求证:BC=DH.
20.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AE=AD.
21.如图,小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一颗树C处,接着再向前走了30步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约0.5米,估计小刚在点A处时他与电线塔的距离,并说明理由.
22.如图,AB∥FC,E是DF的中点.
(1)求证:△ADE≌△CFE;
(2)若AB=10,CF=6,求BD的长.
23.综合与实践
如图1所示,已知△ABC中,∠ACB=90°,AC=BC,直线m经过点C,过A、B两点分别作直线m的垂线,垂足分别为E、F.
(1)如图1,当直线m在A、B两点同侧时,直接写出EF与AE、BF之间的数量关系;
(2)若直线m绕点C旋转到图2所示的位置时(BF<AE),其余条件不变,猜想EF与AE,BF有什么数量关系?并证明你的猜想;
(3)若直线m绕点C旋转到图3所示的位置时(BF>AE)其余条件不变,问EF与AE,BF的数量关系如何?直接写出猜想结论,不需证明.
参考答案
1.D
解:,,
.
在与中,
.
故选:D.
2.C
解:带③去,理由如下:
∵③中满足ASA的条件,
∴带③去,
故选C.
3.D
解:,,为公共角,
,
,故①符合题意;
,即,且,(对顶角相等),
,
,故②符合题意,
∴;
连接,
,,为公共边,
,
,即平分,③符合题意.
综上得①②③均正确.
故选:D.
4.D
解:∵,,,
∴,,,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
故选:D.
5.B
解:被墨迹污染的三角形,已知两个角与这两个角所夹的边,故由ASA即可画出三角形,其依据是ASA.
故选:B.
6.C
解:∵CF∥AB,
∴∠1=∠F,∠2=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中,
∠1=∠F,∠A=∠2,AE=EC,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB AD=9 6.5=2.5,
故选:C.
7.C
解:如图,延长CE′和BA相交于点F,
由翻折可知:
∠BE'C=∠E=90°,CE'=CE=1,
∵BE'是∠ABC的角平分线,
∴∠CBE'=∠FBE',
∵BE′=BE′,
∴△BE'C △BE'F(ASA),
∴E'F=CE'=1,
∴CF=2,
∵∠FCA+∠F=90°,∠DBA+∠F=90°,
∴∠FCA=∠DBA,
∵∠FAC=∠DAB=90°,AB=AC,
∴△FCA △DBA(ASA),
∴BD=CF=2.
故选:C.
8.D
解:连接,如图所示,
为等腰直角三角形,点为的中点,
,,.
,,
.
在和中,
,
,
,
,
则结论①正确;
,,,
,
则结论②正确;
,
,
,
则结论③正确.
故选:.
9.A
解:设AB、DC相交于点O,
∵∠1=∠2,,
∴,
∴∠B=∠D,
∵∠2=∠3,
∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
在△ACB和△ECD中,
,
∴△ACB≌△ECD(AAS),
∴AB=ED.
故选:A.
10.D
解:如图,延长ED交AB于点F,
∵△BDA沿BD对折得到△BDE,
∴△BDA≌△BDE,
∴∠ABD=∠DBE,DA=DE,
故A正确,不符合题意;
由△BDA≌△BDE可知,
∠A=∠E,AB=BE,
在△ABC和△EBF中,
,
∴△ABC≌△EBF(ASA),
∴BC=BF,
在△FBD和△CBD中,
,
∴△FBD≌△CBD(SAS),
∴∠DCB=∠DFB=90°,DF=DC,
∴∠ABC=∠CDE,
∴∠CDE=2∠ABD,
故B正确,不符合题意;
∵∠BDE=∠BDC+∠CDE=∠BDC+2∠ABD,
∴∠BDE﹣∠ABD
=∠BDC+2∠ABD﹣∠ABD
=∠BDC+∠ABD
=∠BDC+∠DBC
=90°,
故C正确,不符合题意;
S△ABD= AB DF,S△CDE= CE CD,
∴==,
故D错误,符合题意;
故选:D.
11.A
解:∵AB∥CD
∴∠B=∠C,∠BEM=∠CFM
∵M是BC的中点
∴BM=CM
∴△EMB≌△FMC(AAS)
∴EM=FM
∴只需要测量出EM的长度即可
故选A.
12.C
解:∵AD⊥BC,
∴∠ADC=90°,
∴∠C+∠DAC=90°,
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∴∠C=∠BAD,
∵EF//AC,
∴∠C=∠BFE,
∴∠BAD=∠BFE,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE和△FBE中,
,
∴△ABE≌△FBE(AAS),
∴AB=BF,
故选:C.
13.D
解:∵OP平分∠AOB,
∴∠POD=∠POC,
∵PD⊥OB,PC⊥OA,
∴∠PCO=∠PDO,
在△POD和△POC中,
,
∴△POC≌△POD(AAS),
∴PC=PD,OC=OD,∠CPO=∠DPO,故A,B,C正确;
故选:D.
14.5
解:∵∠AOC=∠D+∠C,∠BOD=∠A+∠B,∠A=∠C,∠AOC=∠BOD,
∴∠B=∠D,
在△AOB和△COD中,
∵,
∴△AOB≌△COD,
∴OA=OC,DO=OB,
∴OC=OA=AD-OD= AD-OB =8-3=5,
∴OC的长为5
故答案为:5
15.8
解:
如图所示,延长AP交BC于D,
BP平分∠ABC,
,
,
,
在和中,
,
,
,
,,
,
故答案为:8.
16.
解:,
,
,,
,
,
故答案为:100
17.1
解:根据点到直线的距离可知,当轴时,最小,如下图:
则,,
∴
∴
∴
∴
故答案为1
18.1或2或1
解:在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS),
∴∠A=∠E,
在△ACP和△ECQ中,
,
∴△ACP≌△ECQ(ASA),
∴AP=EQ,
当0≤t≤时,3t=4-t,
解得:t=1;
当<t≤时,8-3t=4-t,
解得:t=2;
综上所述,当线段PQ经过点C时,t的值为1s或2s.
.
19.证明见详解.
解: ∵AC∥EH,
∴∠A=∠E,
在△ABC和△EDH中
,
∴△ABC≌△EDH(AAS),
∴BC=DH.
20.证明见解析
解:∵AB=AC,∠B=∠C
∴
∴(ASA)
∴.
21.(1)答案见解析;(2)40米
解:(1)根据题意可知步,步.
故可画示意图如下:
(2)根据题意可知:,
∴在和中 ,
∴,
∴AB=ED=80步
小刚一步大约0.5米,
∴小刚在点A处时他与电线塔的距离为米.
22.(1)见解析;(2)4
解:(1)∵,
∴,
∵是的中点,
∴,
在和中,
,
∴,
(2)∵,
∴,
∴.
23.(1)EF=AE+BF;(2)EF=AE﹣BF,证明见解析;(3)EF=BF﹣AE
解:(1)EF=AE+BF;
证明如下:∵
∴
由题意得:,
∴,
∴
在和中
∴
∴、
又∵
∴
(2)EF=AE﹣BF
∵∠ACB=90°,
∴∠ACE+∠FCB=90°,
又∵AE⊥m,BF⊥m,
∴∠AEC=90°,∠BFC=90°,
∴∠CAE+∠ACE=90°,
∴∠CAE=∠FCB,
又∵AC=BC,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CF﹣CE=AE﹣BF;
(3)EF=BF﹣AE
∵∠ACB=90°,
∴∠ACE+∠FCB=90°,
又∵AE⊥m,BF⊥m,
∴∠AEC=90°,∠BFC=90°,
∴∠CAE+∠ACE=90°,
∴∠CAE=∠FCB,
又∵AC=BC,
∴△ACE≌△CBF(AAS),
∴AE=CF,CE=BF,
∴EF=CE﹣CF=BF﹣AE;
