2021-2022学年华东师大版数学八年级上册13.2.5三角形全等的判定——边边边课时练习(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册13.2.5三角形全等的判定——边边边课时练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 452.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览


文档简介
三角形全等的判定——边边边
一、单选题
1.用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是( )
A.SAS B.ASA C.AAS D.
2.如图,在下列条件中,不能证明的是( )
A., B.,
C., D.,
3.如图,下面是利用尺规作∠AOB的平分线OC的作法:
(1)以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
(2)分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于点C;
(3)画射线OC,射线OC就是∠AOB的平分线.
在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
A.ASA B.SAS C.SSS D.AAS
4.如果两个三角形的两条边和其中一条边上的中线分别对应相等,那么这两个三角形第三条边所对的角的关系是( )
A.相等 B.互余 C.互补 D.以上答案都不正确
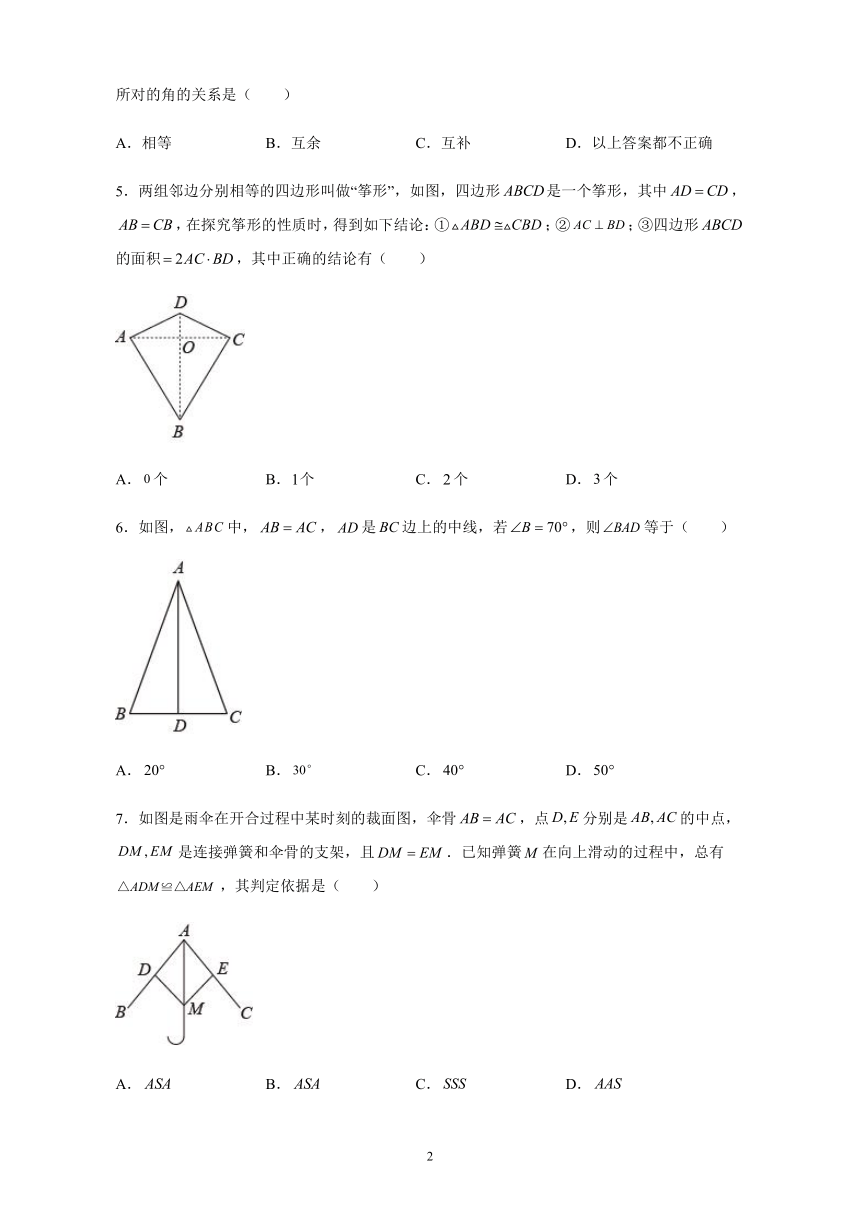
5.两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中,,在探究筝形的性质时,得到如下结论:①;②;③四边形的面积,其中正确的结论有( )
A.个 B.个 C.个 D.个
6.如图,中,,是边上的中线,若,则等于( )
A. B. C. D.
7.如图是雨伞在开合过程中某时刻的裁面图,伞骨,点分别是的中点,是连接弹簧和伞骨的支架,且.已知弹簧在向上滑动的过程中,总有,其判定依据是( )
A. B. C. D.
8.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,这里根据是( )
A.SAS B.ASA C.HL D.SSS
9.小强家有两块三角形的菜地,他想判断这两块三角形菜地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定能判断两个三角形全等的是( )
A.测量三边对应相等 B.测量两角及其夹边对应相等
C.测量两边及除夹角外的另一角对应相等 D.测量两边及其夹角对应相等
10.在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与全等,这样的格点三角形一共可以作出( )
A.2个 B.3个 C.4个 D.6个
11.平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
A.110° B.125° C.130° D.135°
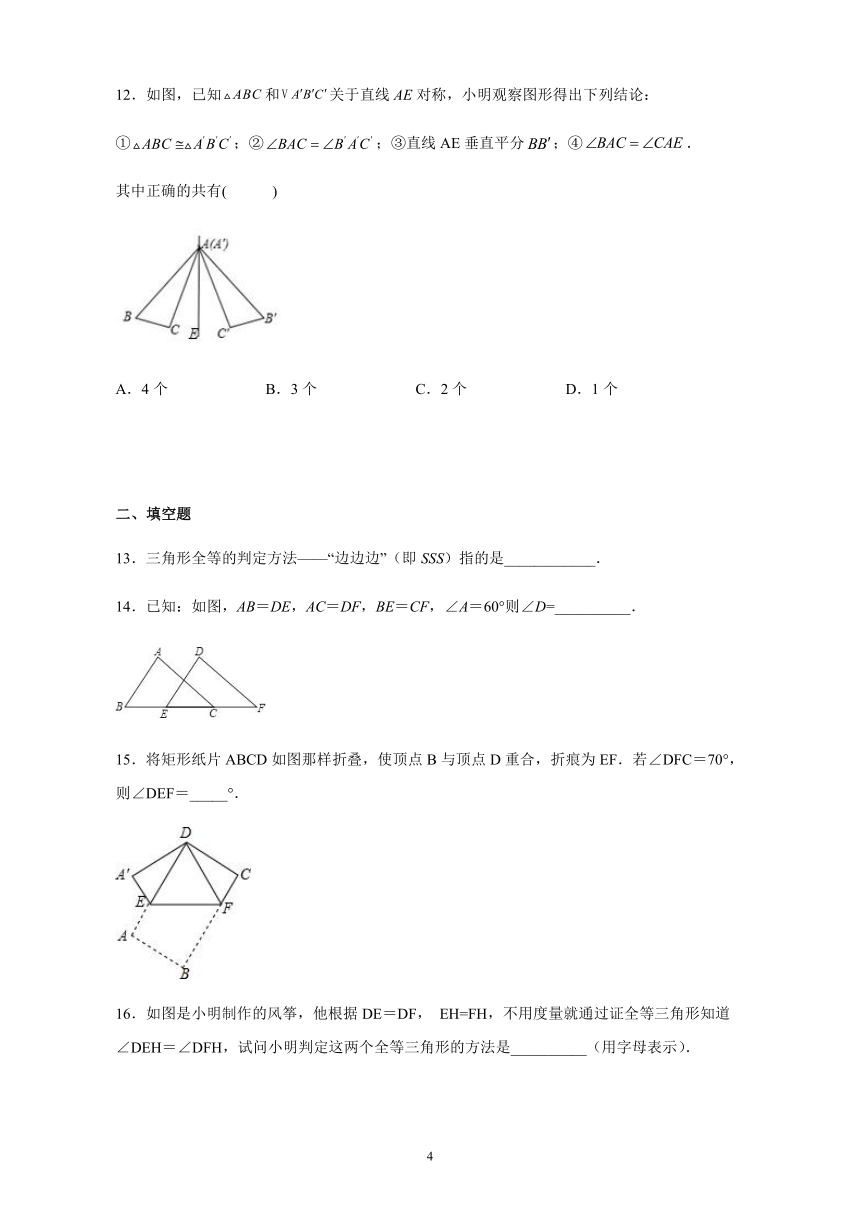
12.如图,已知和关于直线AE对称,小明观察图形得出下列结论:
①;②;③直线AE垂直平分;④.
其中正确的共有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
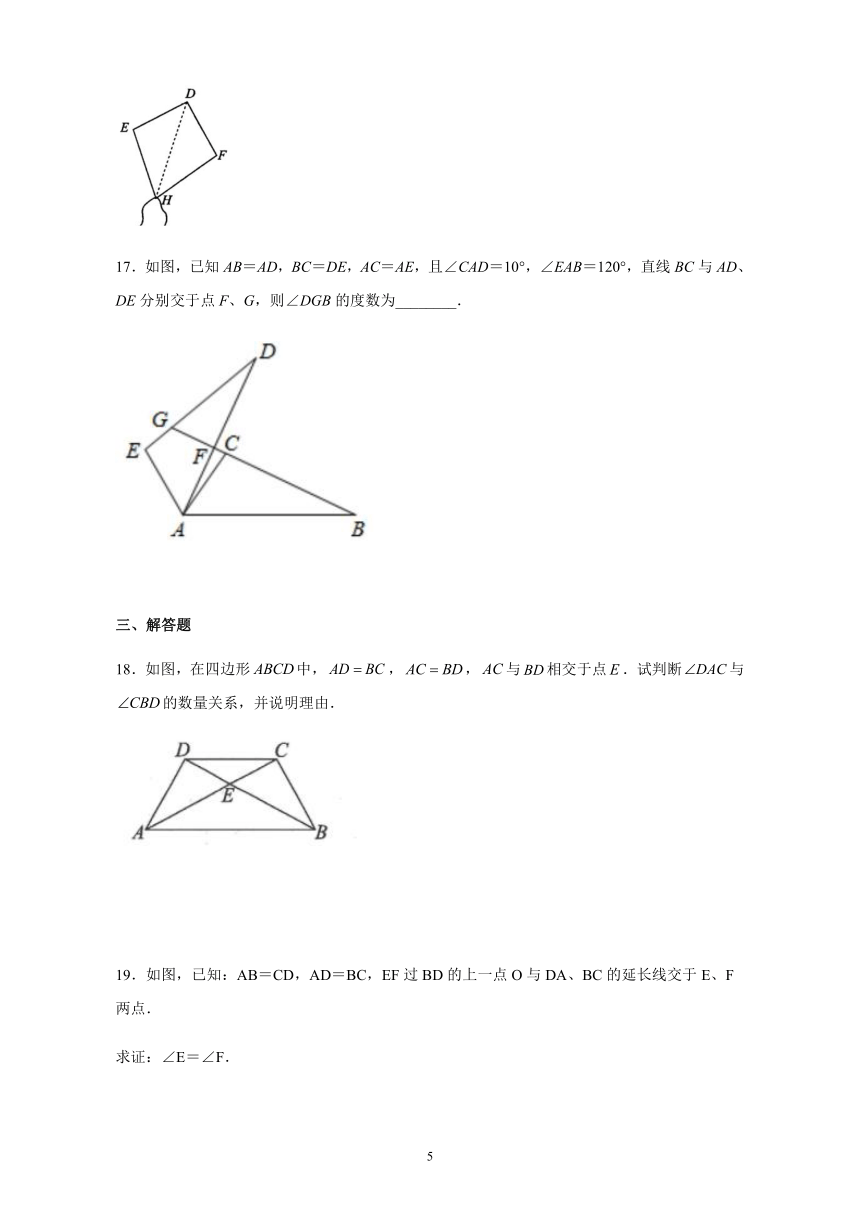
13.三角形全等的判定方法——“边边边”(即SSS)指的是____________.
14.已知:如图,AB=DE,AC=DF,BE=CF,∠A=60°则∠D=__________.
15.将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=_____°.
16.如图是小明制作的风筝,他根据DE=DF, EH=FH,不用度量就通过证全等三角形知道∠DEH=∠DFH,试问小明判定这两个全等三角形的方法是__________(用字母表示).
17.如图,已知AB=AD,BC=DE,AC=AE,且∠CAD=10°,∠EAB=120°,直线BC与AD、DE分别交于点F、G,则∠DGB的度数为________.
三、解答题
18.如图,在四边形中,,,与相交于点.试判断与的数量关系,并说明理由.
19.如图,已知:AB=CD,AD=BC,EF过BD的上一点O与DA、BC的延长线交于E、F两点.
求证:∠E=∠F.
20.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.
求证:(1)∠D=∠B;
(2)OE=OF.
21.如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.
参考答案
1.D
解:由作图可知,
在△BDE和△中,
,
∴△BDE≌△(SSS),
∴∠EBD=∠,
故选D.
2.D
解:根据题意知,边为公共边.
A.由“SSS”可以判定,在△ABC和△DCB中,BC=CB,,,∴(SSS);故选项A不符合题意;
B.由“SAS”可以判定,在△ABC和△DCB中,,,BC=CB,∴(SAS);故选项B不符合题意;
C.∵∴,在△ABC和△DCB中,,,BC=CB,∴(AAS);则由“AAS”可以判定,故选项C项不符合题意;
D.∵,BC=CB,但不是两边的夹角,在一般三角形中,没有“SSA”判定方法,∴不能证明,故选项D符合题意.
故选:D.
3.C
解:连接EC,DC,根据作图的过程可知
在和中,
,
∴;
故选C.
4.A
解:如图,在和中,,分别是两个三角形的中线,,,,则.
理由:在和中,,分别是两个三角形的中线,
,,
,
,
,,
∴(SSS),
,
这两个三角形的第三条边所对的角的关系是相等,
故选A.
5.C
解:在与中,
,
,故①正确;
,
在与中,
,
,
,,
,故②正确;
四边形的面积,故③错误;
故选:C.
6.A
解:∵AD为BC边上的中线,
∴BD=CD,
在△ABD和ACD中
,
∴△ABD≌ACD,
∴∠C=,∠BAD=∠CAD,
∴∠BAC=180°-70°-70°=40°,
∴∠BAD=∠CAD=∠BAC=20°,
故选:A.
7.C
解:∵分别是的中点,
∴,,
∵,
∴,
在△ADM和△AEM中,
,
∴△ADM≌△AEM(SSS).
故选:C.
8.D
解:在和中,
射线OC是的平分线
故选:D.
9.C
解:全等三角形的判定方法有:SSS,SAS,ASA,AAS;
A:根据SSS,两个三角形全等;
B:根据ASA,两个三角形全等;
C:两个三角形不一定不全等;
D:根据SAS,两个三角形全等;
故选:C.
10.C
解:根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故选:C.
11.C
解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°-75°-155°=130°,
故选:C.
12.B
解:和关于直线AE对称,
,结论②正确;
点和点关于直线AE对称,则直线AE垂直平分,结论③正确;
,
,结论①正确;
与不一定相等,则结论④错误;
综上,正确的共有3个,
故选:B.
13.三边对应相等的两个三角形全等.
解:“边边边”(即SSS)指的是“三边对应相等的两个三角形全等”.
故答案是:三边对应相等的两个三角形全等.
14.60°
解:∵BE=CF ,
∴BE+EC=CF+EC,
∴BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
∴∠A=∠D=60°,
故答案为:60°.
15.55
解:根据折叠的性质可知:四边形ABFE和四边形A′DFE全等,
∴∠A′=∠A=90°,∠DFE=∠BFE,A′D=AB=CD,
在Rt△A′DE和Rt△CDF中,,
∴Rt△A′DE≌Rt△CDF,
∴DE=DF,
∴∠DEF=∠DFE,
∵∠DFC=70°,
∴∠DFE=∠BFE=55°,
∴∠DEF=55°.
故答案为55.
16.SSS
解:∵在△DEH和△DFH中,
,
∴△DEH≌△DFH(SSS),
∴∠DEH=∠DFH.
故答案为:SSS.
17.65°
解:∵AB=AD,BC=DE,AC=AE,
∴△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D;
∵∠EAB=120°,
∴∠DAE+∠CAD+∠BAC=120°,
∵∠CAD=10°,
∴∠BAC=(120°-10°)=55°,
∴∠BAF=∠BAC+∠CAD=65°,
∵∠B=∠D,∠DFG=∠BFA,
∴∠DGB=∠BAF =65°.
18.,理由见解析
解:.
理由:在和中,
,
,
.
19.见解析
解:在△ABD和△CDB中
∵AB=CD,AD=BC,BD=DB,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,
∴DE∥BF.
∴∠E=∠F.
20.(1)证明见解析;(2)证明见解析.
解:(1)在和中,
,
,
.
(2)在和中,
,
,
,
,
.
21.详见解析.
解:∠1与∠2相等.
在△ADC与△CBA中,
,
∴△ADC≌△CBA.(SSS)
∴∠DAC=∠BCA.
∴DA∥BC.
∴∠1=∠2.
②③图形同理可证,△ADC≌△CBA得到∠DAC=∠BCA,则DA∥BC,∠1=∠2.
一、单选题
1.用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是( )
A.SAS B.ASA C.AAS D.
2.如图,在下列条件中,不能证明的是( )
A., B.,
C., D.,
3.如图,下面是利用尺规作∠AOB的平分线OC的作法:
(1)以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
(2)分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于点C;
(3)画射线OC,射线OC就是∠AOB的平分线.
在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
A.ASA B.SAS C.SSS D.AAS
4.如果两个三角形的两条边和其中一条边上的中线分别对应相等,那么这两个三角形第三条边所对的角的关系是( )
A.相等 B.互余 C.互补 D.以上答案都不正确
5.两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中,,在探究筝形的性质时,得到如下结论:①;②;③四边形的面积,其中正确的结论有( )
A.个 B.个 C.个 D.个
6.如图,中,,是边上的中线,若,则等于( )
A. B. C. D.
7.如图是雨伞在开合过程中某时刻的裁面图,伞骨,点分别是的中点,是连接弹簧和伞骨的支架,且.已知弹簧在向上滑动的过程中,总有,其判定依据是( )
A. B. C. D.
8.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,这里根据是( )
A.SAS B.ASA C.HL D.SSS
9.小强家有两块三角形的菜地,他想判断这两块三角形菜地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定能判断两个三角形全等的是( )
A.测量三边对应相等 B.测量两角及其夹边对应相等
C.测量两边及除夹角外的另一角对应相等 D.测量两边及其夹角对应相等
10.在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与全等,这样的格点三角形一共可以作出( )
A.2个 B.3个 C.4个 D.6个
11.平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
A.110° B.125° C.130° D.135°
12.如图,已知和关于直线AE对称,小明观察图形得出下列结论:
①;②;③直线AE垂直平分;④.
其中正确的共有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
13.三角形全等的判定方法——“边边边”(即SSS)指的是____________.
14.已知:如图,AB=DE,AC=DF,BE=CF,∠A=60°则∠D=__________.
15.将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=_____°.
16.如图是小明制作的风筝,他根据DE=DF, EH=FH,不用度量就通过证全等三角形知道∠DEH=∠DFH,试问小明判定这两个全等三角形的方法是__________(用字母表示).
17.如图,已知AB=AD,BC=DE,AC=AE,且∠CAD=10°,∠EAB=120°,直线BC与AD、DE分别交于点F、G,则∠DGB的度数为________.
三、解答题
18.如图,在四边形中,,,与相交于点.试判断与的数量关系,并说明理由.
19.如图,已知:AB=CD,AD=BC,EF过BD的上一点O与DA、BC的延长线交于E、F两点.
求证:∠E=∠F.
20.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.
求证:(1)∠D=∠B;
(2)OE=OF.
21.如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.
参考答案
1.D
解:由作图可知,
在△BDE和△中,
,
∴△BDE≌△(SSS),
∴∠EBD=∠,
故选D.
2.D
解:根据题意知,边为公共边.
A.由“SSS”可以判定,在△ABC和△DCB中,BC=CB,,,∴(SSS);故选项A不符合题意;
B.由“SAS”可以判定,在△ABC和△DCB中,,,BC=CB,∴(SAS);故选项B不符合题意;
C.∵∴,在△ABC和△DCB中,,,BC=CB,∴(AAS);则由“AAS”可以判定,故选项C项不符合题意;
D.∵,BC=CB,但不是两边的夹角,在一般三角形中,没有“SSA”判定方法,∴不能证明,故选项D符合题意.
故选:D.
3.C
解:连接EC,DC,根据作图的过程可知
在和中,
,
∴;
故选C.
4.A
解:如图,在和中,,分别是两个三角形的中线,,,,则.
理由:在和中,,分别是两个三角形的中线,
,,
,
,
,,
∴(SSS),
,
这两个三角形的第三条边所对的角的关系是相等,
故选A.
5.C
解:在与中,
,
,故①正确;
,
在与中,
,
,
,,
,故②正确;
四边形的面积,故③错误;
故选:C.
6.A
解:∵AD为BC边上的中线,
∴BD=CD,
在△ABD和ACD中
,
∴△ABD≌ACD,
∴∠C=,∠BAD=∠CAD,
∴∠BAC=180°-70°-70°=40°,
∴∠BAD=∠CAD=∠BAC=20°,
故选:A.
7.C
解:∵分别是的中点,
∴,,
∵,
∴,
在△ADM和△AEM中,
,
∴△ADM≌△AEM(SSS).
故选:C.
8.D
解:在和中,
射线OC是的平分线
故选:D.
9.C
解:全等三角形的判定方法有:SSS,SAS,ASA,AAS;
A:根据SSS,两个三角形全等;
B:根据ASA,两个三角形全等;
C:两个三角形不一定不全等;
D:根据SAS,两个三角形全等;
故选:C.
10.C
解:根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故选:C.
11.C
解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°-75°-155°=130°,
故选:C.
12.B
解:和关于直线AE对称,
,结论②正确;
点和点关于直线AE对称,则直线AE垂直平分,结论③正确;
,
,结论①正确;
与不一定相等,则结论④错误;
综上,正确的共有3个,
故选:B.
13.三边对应相等的两个三角形全等.
解:“边边边”(即SSS)指的是“三边对应相等的两个三角形全等”.
故答案是:三边对应相等的两个三角形全等.
14.60°
解:∵BE=CF ,
∴BE+EC=CF+EC,
∴BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
∴∠A=∠D=60°,
故答案为:60°.
15.55
解:根据折叠的性质可知:四边形ABFE和四边形A′DFE全等,
∴∠A′=∠A=90°,∠DFE=∠BFE,A′D=AB=CD,
在Rt△A′DE和Rt△CDF中,,
∴Rt△A′DE≌Rt△CDF,
∴DE=DF,
∴∠DEF=∠DFE,
∵∠DFC=70°,
∴∠DFE=∠BFE=55°,
∴∠DEF=55°.
故答案为55.
16.SSS
解:∵在△DEH和△DFH中,
,
∴△DEH≌△DFH(SSS),
∴∠DEH=∠DFH.
故答案为:SSS.
17.65°
解:∵AB=AD,BC=DE,AC=AE,
∴△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D;
∵∠EAB=120°,
∴∠DAE+∠CAD+∠BAC=120°,
∵∠CAD=10°,
∴∠BAC=(120°-10°)=55°,
∴∠BAF=∠BAC+∠CAD=65°,
∵∠B=∠D,∠DFG=∠BFA,
∴∠DGB=∠BAF =65°.
18.,理由见解析
解:.
理由:在和中,
,
,
.
19.见解析
解:在△ABD和△CDB中
∵AB=CD,AD=BC,BD=DB,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,
∴DE∥BF.
∴∠E=∠F.
20.(1)证明见解析;(2)证明见解析.
解:(1)在和中,
,
,
.
(2)在和中,
,
,
,
,
.
21.详见解析.
解:∠1与∠2相等.
在△ADC与△CBA中,
,
∴△ADC≌△CBA.(SSS)
∴∠DAC=∠BCA.
∴DA∥BC.
∴∠1=∠2.
②③图形同理可证,△ADC≌△CBA得到∠DAC=∠BCA,则DA∥BC,∠1=∠2.
