2021-2022学年华东师大版数学八年级上册13.2.6三角形全等的判定—斜边直角边课时练习(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册13.2.6三角形全等的判定—斜边直角边课时练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 18:12:04 | ||
图片预览



文档简介
三角形全等的判定——斜边直角边
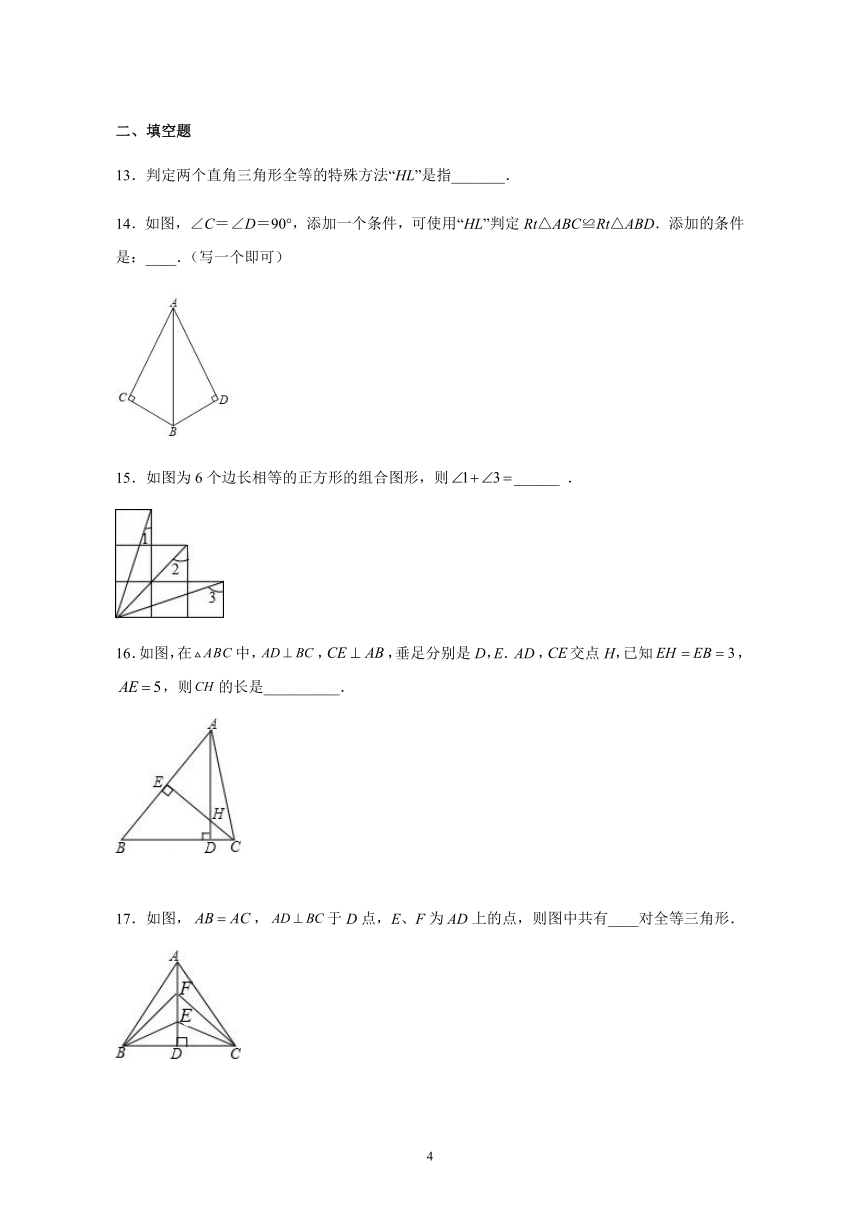
一、单选题
1.如图,于点D,,E在AD上,则图中全等的三角形共有几对( )
A.4对 B.3对 C.2对 D.1对
2.如图,∠A=∠D=90°,AC=DB,则ABC≌DCB的依据是( )
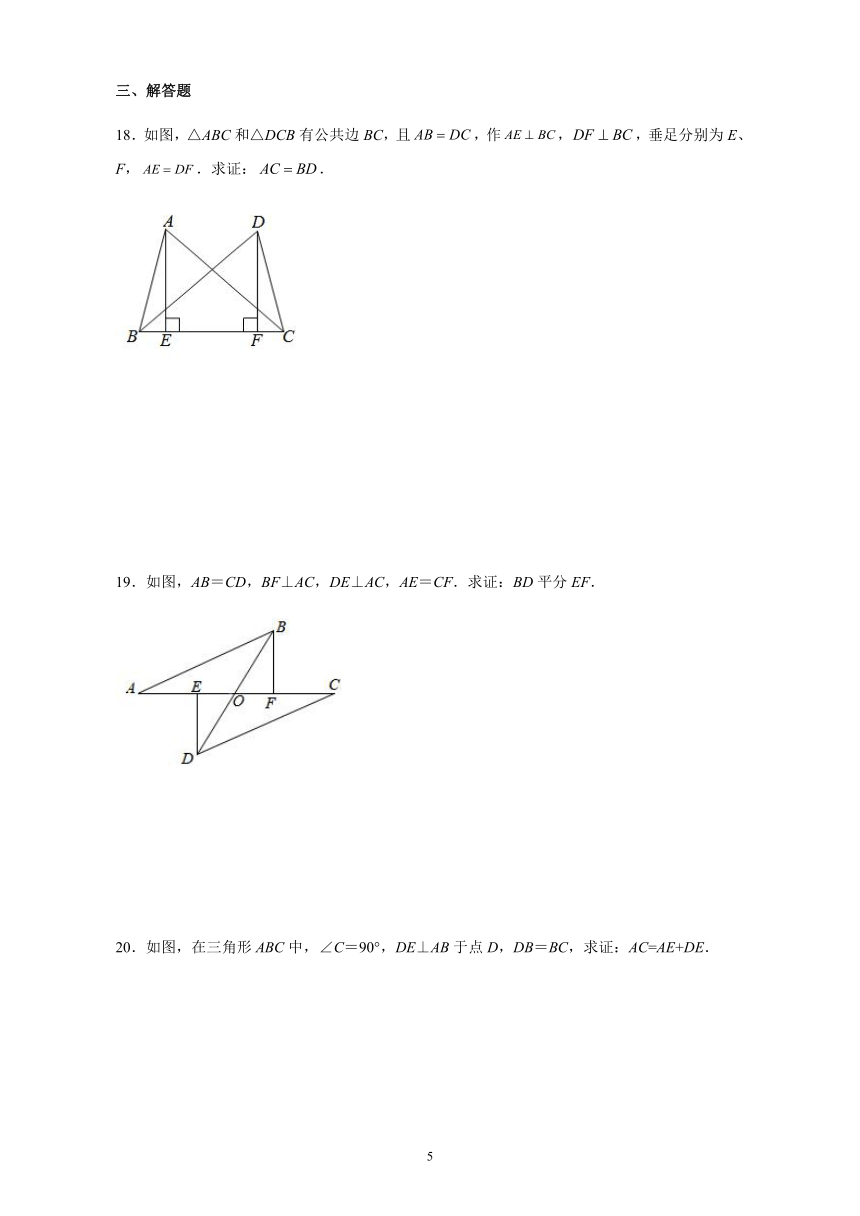
A.HL B.ASA C.AAS D.SAS
3.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,则两个木桩离旗杆底部的距离与的距离间的关系是( )
A. B. C. D.不能确定
4.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.ASA B.AAS C.SAS D.HL
5.如图,AD是ABC的高,下列不能使ABD≌ACD的条件是( )
A.BD=CD B.∠BAC=90° C.∠B=∠C D.AB=AC
6.如果两个三角形中两条边分别相等,且相等的一对边上的高也相等,那么这两个三角形的第三条边所对的角的关系是( )
A.相等 B.不相等 C.互余或相等 D.互补或相等
7.如图,于点D,于点E,下列条件:①OP是的平分线;②;③;④;其中能够证明的条件的个数有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是 ( )
A.45° B.60° C.90° D.120°
9.如图,在Rt△ABC中,∠C = 90°,∠B =30°,D是BC上一点,DE⊥AB于点E,且DE=DC,则∠CAD的度数为( )
A.15° B.20° C.25° D.30°
10.如图,,,垂足分别为、,且,则直接判定与全等的理由是( )
A.SAS B.AAS C.SSS D.HL
11.如图,,,,垂足分别为,,要使,则所需添加的条件不正确的是( )
A. B. C. D.
12.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A.2 B.3 C.4 D.8
二、填空题
13.判定两个直角三角形全等的特殊方法“HL”是指_______.
14.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC≌Rt△ABD.添加的条件是:____.(写一个即可)
15.如图为6个边长相等的正方形的组合图形,则______ .
16.如图,在中,,,垂足分别是D,E.,交点H,已知,,则的长是__________.
17.如图,,于D点,E、F为AD上的点,则图中共有____对全等三角形.
三、解答题
18.如图,△ABC和△DCB有公共边BC,且,作,,垂足分别为E、F,.求证:.
19.如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.求证:BD平分EF.
20.如图,在三角形ABC中,∠C=90°,DE⊥AB于点D,DB=BC,求证:AC=AE+DE.
21.用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使,再过点M画的垂线,过点N画的垂线,两垂线交于点P,那么射线就是的平分线.请你证明这一结论.
22.如图,在长方形ABCD中,,延长BC到E,使,连接DE.动点P从点B出发,以每秒2个单位的速度沿向终点A运动,设点P运动的时间为t秒,存在这样的t,使和△DCE全等,则t的值为多少?
参考答案
1.B
解:,
又,
,
又.
故图中全等的三角形共有3对.
故选B.
2.A
解:∵∠A=∠D=90°,
∴在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
故选:A.
3.C
解:,
,
由,,
,
.
故选:C.
4.A
解:由图可得,三角形已知一个锐角和一个直角,以及两角的夹边,
所以根据ASA证明三角形全等,
故选:A.
5.B
解:A. AD是ABC的高,
,
当BD=CD时,在与 中,
,
;
B.当∠BAC=90°时,条件不够,不能得出;
C. 当∠B=∠C时,在与 中,
,
;
D. 当AB=AC时,在与 中,
,
.
故选:B.
6.D
解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,, 高,
延长 与高交于,
,
在和中,
,
,
,
此时,,
是互补关系,
综上所述,这两个三角形的第三条边所对的角的关系是“相等或互补”.
故选:.
7.D
解:∵OP是∠AOB的平分线,
∴∠DOP=∠EOP,
∵PD⊥AO于D,PE⊥BO于E,
∴∠PEO=∠PDO=90°
又∵OP=OP,
∴△DOP≌△EOP(AAS),故①正确;
∵PD⊥AO于D,PE⊥BO于E,
∴∠PEO=∠PDO=90°,
∵DP=EP,OP=OP,
∴Rt△DOP≌Rt△EOP(HL),故②正确;
∵FD⊥AO于D,FE⊥BO于E,
∴∠PEO=∠PDO=90°,
∵DO=EO,OP=OP,
∴Rt△DOP≌Rt△EOP(HL),故③正确;
∵PD⊥AO于D,PE⊥BO于E,
∴∠PEO=∠PDO=90°,
又∵∠OPD=OPE,OP=OP,
∴△DOP≌△EOP(AAS),故④正确
∴能够证明△DOP≌△EOP的条件的个数有四个.
故选D.
8.C
解:∵BD⊥AE于D,CE⊥AE于E,
∴∠ADB=∠E=90,
在Rt△BAD和Rt△ACE中,
AB=AC、 AD=EC
∴△BAD≌△CAE(HL),
∴∠BAD=∠ACE,
∵∠ACE+∠CAE=90°,
∴∠BAC =∠BAD+∠CAE=90°.
故选C.
9.D
解:∵∠C = 90°,∠B =30°,
∴∠BAC=60°,
∵DE⊥AB,且DE=DC,
∴∠DEA=∠C=90°,
又∵AD=AD,
∴△ACD≌△AED(HL),
∴∠EAD=∠CAD,
∵∠EAD+∠CAD=∠BAC=60°,
∴∠CAD=30°,
故选D.
10.D
解:,,
,
在和中,
,
故选:D.
11.D
解:在△ABF与△CDE中,AB=CD,
由DE⊥AC,BF⊥AC,可得∠BFA=∠DEC=90°.
A、添加DE=BF后,满足HL,符合题意;
B、添加ABCD,即∠A=∠C后,满足AAS,符合题意;
C、添加AE=CF,即AF=CE后,满足HL,符合题意;
D、添加AE=EF后,无法证明,故D选项不符合题意;
故选:D.
12.C
解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
∴AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故选:C.
13.斜边和一条直角边分别相等的两个直角三角形全等
解:判定两个直角三角形全等的特殊方法“HL”是指斜边直角边公理,
即斜边和一条直角边分别相等的两个直角三角形全等,
故答案为:斜边和一条直角边分别相等的两个直角三角形全等
14.AC=AD
解:添加的条件是AC=AD,
理由是:∵∠C=∠D=90°,
∴在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL),
故答案为:AC=AD(答案不唯一).
15.90°
解:观察图形可知:△ABC≌△BDE,
∴∠1=∠DBE,
又∵∠DBE+∠3=90°,
∴∠1+∠3=90°.
故答案为:90°.
16.2
解:,,
,
,
,
在与中,
,
,
,
.
故答案为:2.
17.6
解:∵AB=AC,AD⊥BC,
∴AD为BC的垂直平分线,BD=CD,∠BAD=∠CAD
∴EB=EC,FB=FC,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
同理可得△EBD≌△ECD,△ABE≌△ACE,△FBD≌△FCD,△ABF≌△ACF,△FBE≌△FCE,
∴共有6对三角形全等,
故答案为:6.
18.见解析
解:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,
∵AB=DC,AE=DF,
∴Rt△ABE≌Rt△DCF(HL).
∴∠ABE=∠DCF.
∵AB=DC,BC=CB,,
∴△ABC≌△DCB(SAS).
∴AC=BD.
19.见解析
解:∵BF⊥AC,DE⊥AC,
∴,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF,
在△DEO和△BFO中,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∴BD平分EF.
20.见解析
解:∵∠C=90°,DE⊥AB,
∴∠EDB=∠C=90°,
在Rt△BED和Rt△BEC中,
,
∴Rt△BED≌Rt△BEC(HL),
∴DE=CE,
∴AC=AE+EC=AE+DE.
21.证明见解析
解:∵∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠POM=∠PON,
∴射线OP就是∠AOB的平分线.
22.或
解:(1)当P在BC上时,由题意得,
∴,
∵,为公共边,
∴要使,则需,如图1所示:
∵,
∴,
∴,
即当时,;
(2)当P在AD上时,由题意得,
∵,,
∴,
∵,为公共边,
∴要使,则需,如图2所示:
即,
∴,
即当时,;
综上所述:当或时,和全等.
一、单选题
1.如图,于点D,,E在AD上,则图中全等的三角形共有几对( )
A.4对 B.3对 C.2对 D.1对
2.如图,∠A=∠D=90°,AC=DB,则ABC≌DCB的依据是( )
A.HL B.ASA C.AAS D.SAS
3.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,则两个木桩离旗杆底部的距离与的距离间的关系是( )
A. B. C. D.不能确定
4.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.ASA B.AAS C.SAS D.HL
5.如图,AD是ABC的高,下列不能使ABD≌ACD的条件是( )
A.BD=CD B.∠BAC=90° C.∠B=∠C D.AB=AC
6.如果两个三角形中两条边分别相等,且相等的一对边上的高也相等,那么这两个三角形的第三条边所对的角的关系是( )
A.相等 B.不相等 C.互余或相等 D.互补或相等
7.如图,于点D,于点E,下列条件:①OP是的平分线;②;③;④;其中能够证明的条件的个数有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在△ABC中,AB=AC,AE是经过点A的一条直线,且B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,AD=CE,则∠BAC的度数是 ( )
A.45° B.60° C.90° D.120°
9.如图,在Rt△ABC中,∠C = 90°,∠B =30°,D是BC上一点,DE⊥AB于点E,且DE=DC,则∠CAD的度数为( )
A.15° B.20° C.25° D.30°
10.如图,,,垂足分别为、,且,则直接判定与全等的理由是( )
A.SAS B.AAS C.SSS D.HL
11.如图,,,,垂足分别为,,要使,则所需添加的条件不正确的是( )
A. B. C. D.
12.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A.2 B.3 C.4 D.8
二、填空题
13.判定两个直角三角形全等的特殊方法“HL”是指_______.
14.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC≌Rt△ABD.添加的条件是:____.(写一个即可)
15.如图为6个边长相等的正方形的组合图形,则______ .
16.如图,在中,,,垂足分别是D,E.,交点H,已知,,则的长是__________.
17.如图,,于D点,E、F为AD上的点,则图中共有____对全等三角形.
三、解答题
18.如图,△ABC和△DCB有公共边BC,且,作,,垂足分别为E、F,.求证:.
19.如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.求证:BD平分EF.
20.如图,在三角形ABC中,∠C=90°,DE⊥AB于点D,DB=BC,求证:AC=AE+DE.
21.用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使,再过点M画的垂线,过点N画的垂线,两垂线交于点P,那么射线就是的平分线.请你证明这一结论.
22.如图,在长方形ABCD中,,延长BC到E,使,连接DE.动点P从点B出发,以每秒2个单位的速度沿向终点A运动,设点P运动的时间为t秒,存在这样的t,使和△DCE全等,则t的值为多少?
参考答案
1.B
解:,
又,
,
又.
故图中全等的三角形共有3对.
故选B.
2.A
解:∵∠A=∠D=90°,
∴在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
故选:A.
3.C
解:,
,
由,,
,
.
故选:C.
4.A
解:由图可得,三角形已知一个锐角和一个直角,以及两角的夹边,
所以根据ASA证明三角形全等,
故选:A.
5.B
解:A. AD是ABC的高,
,
当BD=CD时,在与 中,
,
;
B.当∠BAC=90°时,条件不够,不能得出;
C. 当∠B=∠C时,在与 中,
,
;
D. 当AB=AC时,在与 中,
,
.
故选:B.
6.D
解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,, 高,
延长 与高交于,
,
在和中,
,
,
,
此时,,
是互补关系,
综上所述,这两个三角形的第三条边所对的角的关系是“相等或互补”.
故选:.
7.D
解:∵OP是∠AOB的平分线,
∴∠DOP=∠EOP,
∵PD⊥AO于D,PE⊥BO于E,
∴∠PEO=∠PDO=90°
又∵OP=OP,
∴△DOP≌△EOP(AAS),故①正确;
∵PD⊥AO于D,PE⊥BO于E,
∴∠PEO=∠PDO=90°,
∵DP=EP,OP=OP,
∴Rt△DOP≌Rt△EOP(HL),故②正确;
∵FD⊥AO于D,FE⊥BO于E,
∴∠PEO=∠PDO=90°,
∵DO=EO,OP=OP,
∴Rt△DOP≌Rt△EOP(HL),故③正确;
∵PD⊥AO于D,PE⊥BO于E,
∴∠PEO=∠PDO=90°,
又∵∠OPD=OPE,OP=OP,
∴△DOP≌△EOP(AAS),故④正确
∴能够证明△DOP≌△EOP的条件的个数有四个.
故选D.
8.C
解:∵BD⊥AE于D,CE⊥AE于E,
∴∠ADB=∠E=90,
在Rt△BAD和Rt△ACE中,
AB=AC、 AD=EC
∴△BAD≌△CAE(HL),
∴∠BAD=∠ACE,
∵∠ACE+∠CAE=90°,
∴∠BAC =∠BAD+∠CAE=90°.
故选C.
9.D
解:∵∠C = 90°,∠B =30°,
∴∠BAC=60°,
∵DE⊥AB,且DE=DC,
∴∠DEA=∠C=90°,
又∵AD=AD,
∴△ACD≌△AED(HL),
∴∠EAD=∠CAD,
∵∠EAD+∠CAD=∠BAC=60°,
∴∠CAD=30°,
故选D.
10.D
解:,,
,
在和中,
,
故选:D.
11.D
解:在△ABF与△CDE中,AB=CD,
由DE⊥AC,BF⊥AC,可得∠BFA=∠DEC=90°.
A、添加DE=BF后,满足HL,符合题意;
B、添加ABCD,即∠A=∠C后,满足AAS,符合题意;
C、添加AE=CF,即AF=CE后,满足HL,符合题意;
D、添加AE=EF后,无法证明,故D选项不符合题意;
故选:D.
12.C
解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
∴AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故选:C.
13.斜边和一条直角边分别相等的两个直角三角形全等
解:判定两个直角三角形全等的特殊方法“HL”是指斜边直角边公理,
即斜边和一条直角边分别相等的两个直角三角形全等,
故答案为:斜边和一条直角边分别相等的两个直角三角形全等
14.AC=AD
解:添加的条件是AC=AD,
理由是:∵∠C=∠D=90°,
∴在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL),
故答案为:AC=AD(答案不唯一).
15.90°
解:观察图形可知:△ABC≌△BDE,
∴∠1=∠DBE,
又∵∠DBE+∠3=90°,
∴∠1+∠3=90°.
故答案为:90°.
16.2
解:,,
,
,
,
在与中,
,
,
,
.
故答案为:2.
17.6
解:∵AB=AC,AD⊥BC,
∴AD为BC的垂直平分线,BD=CD,∠BAD=∠CAD
∴EB=EC,FB=FC,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
同理可得△EBD≌△ECD,△ABE≌△ACE,△FBD≌△FCD,△ABF≌△ACF,△FBE≌△FCE,
∴共有6对三角形全等,
故答案为:6.
18.见解析
解:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,
∵AB=DC,AE=DF,
∴Rt△ABE≌Rt△DCF(HL).
∴∠ABE=∠DCF.
∵AB=DC,BC=CB,,
∴△ABC≌△DCB(SAS).
∴AC=BD.
19.见解析
解:∵BF⊥AC,DE⊥AC,
∴,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF,
在△DEO和△BFO中,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∴BD平分EF.
20.见解析
解:∵∠C=90°,DE⊥AB,
∴∠EDB=∠C=90°,
在Rt△BED和Rt△BEC中,
,
∴Rt△BED≌Rt△BEC(HL),
∴DE=CE,
∴AC=AE+EC=AE+DE.
21.证明见解析
解:∵∠OMP=∠ONP=90°,
在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠POM=∠PON,
∴射线OP就是∠AOB的平分线.
22.或
解:(1)当P在BC上时,由题意得,
∴,
∵,为公共边,
∴要使,则需,如图1所示:
∵,
∴,
∴,
即当时,;
(2)当P在AD上时,由题意得,
∵,,
∴,
∵,为公共边,
∴要使,则需,如图2所示:
即,
∴,
即当时,;
综上所述:当或时,和全等.
