2021-2022学年人教版数学八年级上册14.2乘法公式知识点分类训练(word解析版)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册14.2乘法公式知识点分类训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 159.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 18:19:25 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《14.2乘法公式》知识点分类训练(附答案)
一.完全平方公式
1.计算(a﹣2b)2=( )
A.a2﹣4ab+4b2 B.a2+4ab+4b2 C.a2﹣4ab﹣4b2 D.a2+4ab﹣4b2
2.下列计算正确的是( )
A.a6÷a2=a3 B.a2+2a=3a3
C.(﹣2ab2)3=﹣8a3b6 D.(2a+b)2=4a2+b2+2ab
3.(1)已知(a+b)2=6,(a﹣b)2=2,求a2+b2与ab的值;
(2)已知a+b=8,a2b2=9,求a2+b2的值.
4.已知(x+y)2=7,(x﹣y)2=5.
(1)求x2+y2值;
(2)求xy的值.
5.已知x=a﹣2021,y=2027﹣a,xy=5.
(1)求x2+y2的值; (2)求(x﹣y)2的值; (3)求a的值.
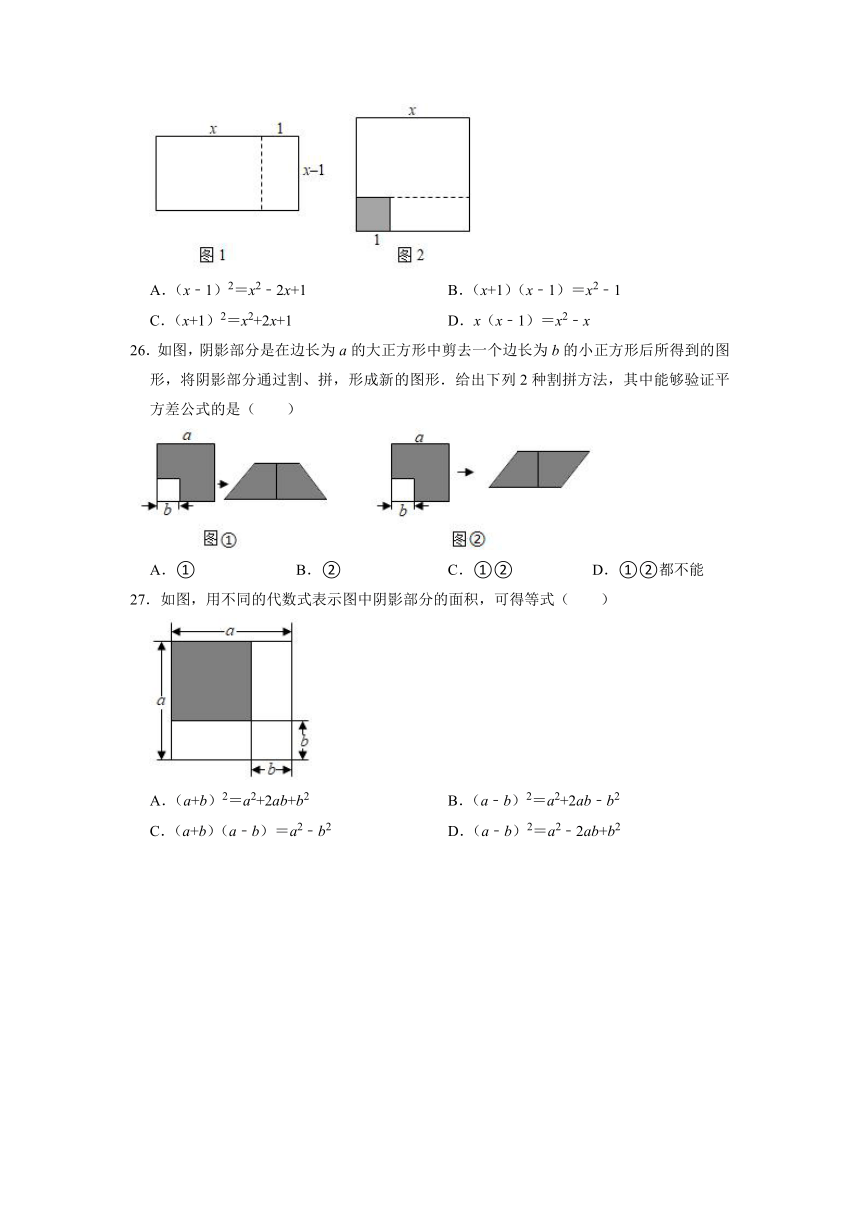
6.已知(n﹣2020)2+(2021﹣n)2=3,求(n﹣2020)(2021﹣n)的值.
二.完全平方公式的几何背景
7.用4块完全相同的长方形拼成如图所示的正方形,用不同的方法计算图中阴影部分的面积,可得到一个关于a,b的等式为( )
A.4a(a+b)=4a2+4ab B.(a+b)(a﹣b)=a2﹣b2
C.(a+b)2=a2+2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
8.用四个完全一样的长方形(长、宽分别设为a、b,a>b)拼成如图所示大正方形,已知大正方形面积为64,中间空缺的小正方形面积为16,则下列关系式中不正确的是( )
A.a2+b2=64 B.a+b=8 C.a﹣b=4 D.a b=12
9.如图,两个正方形的边长分别为a、b,如果a、b满足a+b=6,ab=8,则阴影部分的面积为( )
A.14 B.12 C.9 D.6
10.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC BC=10,则图中阴影部分的面积为 .
三.完全平方式
11.若x2﹣6x+k是完全平方式,则k的值是( )
A.±9 B.9 C.±12 D.12
12.如果x2+8x+m2是一个完全平方式,那么m的值是( )
A.4 B.16 C.±4 D.±16
13.若x2+mx+9是完全平方式,则m的值为( )
A.6 B.9 C.±6 D.±9
14.若多项式9x2﹣2mx+16是一个完全平方式,则m的值为( )
A.±24 B.±12 C.24 D.12
15.若x2+(k﹣1)x+9是完全平方式,则k的值为( )
A.±6 B.7 C.﹣5 D.7或﹣5
四.平方差公式
16.下列不能用平方差公式运算的是( )
A.(x+1)(x﹣1) B.(﹣x+1)(﹣x﹣1)
C.(x+1)(﹣x+1) D.(x+1)(1+x)
17.下列运算正确的是( )
A.(x+y)(﹣y+x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(y﹣x)=x2﹣y2
18.若a+b=6,a2﹣b2=30,则a﹣b=( )
A.5 B.6 C.10 D.15
19.下列多项式的乘法中,能用平方差公式计算的是( )
A.(a+b)(b+a) B.(﹣m+n)(m﹣n)
C.(2x﹣y)(y+2x) D.(x2﹣y)(x+y2)
20.下列算式能用平方差公式计算的是( )
A.(3a+b)(3b﹣a) B.(x+1)(﹣x﹣1)
C.(2x﹣y)(﹣2x+y) D.(﹣n﹣m)(﹣n+m)
21.如果用平方差公式计算(x﹣y+5)(x+y+5),则可将原式变形为( )
A.[(x﹣y)+5][(x+y)+5] B.[(x+5)﹣y][(x+5)+y]
C.[(x﹣y)+5][(x﹣y)﹣5] D.[x﹣(y+5)][x+(y+5)]
22.化简:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2.
23.计算:(x+3)2﹣(x+3)(x﹣3).
五.平方差公式的几何背景
24.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是( )
A.a2+b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
25.如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式( )
A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1
C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x
26.如图,阴影部分是在边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形.给出下列2种割拼方法,其中能够验证平方差公式的是( )
A.① B.② C.①② D.①②都不能
27.如图,用不同的代数式表示图中阴影部分的面积,可得等式( )
A.(a+b)2=a2+2ab+b2 B.(a﹣b)2=a2+2ab﹣b2
C.(a+b)(a﹣b)=a2﹣b2 D.(a﹣b)2=a2﹣2ab+b2
参考答案
一.完全平方公式
1.解:原式=a2﹣2a 2b+(2b)2
=a2﹣4ab+4b2,
故选:A.
2.解:A.a6÷a2=a4,原说法错误,故选项不符合题意;
B.a2和2a不能合并,,原说法错误,故选项不符合题意;
C.(﹣2ab2)3=﹣8a3b6,正确,故选项符合题意;
D.(2a+b)2=4a2+b2+4ab,原说法错误,故选项不符合题意;
故选:C.
3.解:(1)∵(a+b)2=6,(a﹣b)2=2,
∴a2+2ab+b2=6①,a2﹣2ab+b2=2②,
∴①+②得:
a2+2ab+b2+a2﹣2ab+b2=8,
则a2+b2=4;
①﹣②得:
4ab=4,
则ab=1;
(2)∵a+b=8,a2b2=9,
∴(a+b)2=64,ab=±3,
∴a2+2ab+b2=64,
∴a2+b2=64﹣2ab=64﹣2×3=58,或a2+b2=64﹣2ab=64﹣2×(﹣3)=70,
即a2+b2的值是58或70.
4.解:(1)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①+②得:
x2+2xy+y2+x2﹣2xy+y2=12,
则x2+y2=6;
(2)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①﹣②得:
4xy=2,
解得:xy=.
5.解:(1)∵x=a﹣2021,y=2027﹣a,xy=5,
∴x+y=a﹣2021+2027﹣a=6.
∴x2+y2=(x+y)2﹣2xy=62﹣2×5=36﹣10=26.
(2)由(1)知:x2+y2=26.
∴(x﹣y)2=x2+y2﹣2xy=26﹣2×5=16.
(3)由(2)知:(x﹣y)2=16.
∴x﹣y=4或x﹣y=﹣4.
当x﹣y=4时,由x+y=6,解得x=5,y=1,此时a=x+2021=2026.
当x﹣y=﹣4时,由x+y=6,解得x=1,y=5,此时a=x+2021=2022.
综上:a=2026或a=2022.
6.解:令n﹣2020=a,2021﹣n=b,
根据题意得:
a2+b2=3,a+b=1,
∴原式=ab
=
=
=﹣1.
二.完全平方公式的几何背景
7.解:∵图形中大正方形的面积为(a+b)2,
中间空白正方形的面积为(a﹣b)2,
∴图中阴影部分的面积为(a+b)2﹣(a﹣b)2,
又∵图中阴影部分的面积还可表示为4ab,
∴(a+b)2﹣(a﹣b)2=4ab,
故选:D.
8.解:∵大正方形的面积为64,中间空缺的小正方形的面积为16,
∴大正方形的边长为8,小正方形的边长为4,
即:a+b=8,a﹣b=4,
因此a=6,b=2,
∴a2+b2=36+4=40,ab=6×2=12,
故选:A.
9.解:由各个部分面积之间的关系可得,
S阴影部分=S正方形ABCD+S正方形AEFG﹣S△BCD﹣S△BEF
=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab]
=(62﹣3×8)
=6,
故选:D.
10.(1)∵a2+b2=8,(a+b)2=48,
∴ab===20,
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)] ﹣2(25﹣x)(x﹣10)
=15 ﹣2×(﹣15)
=225+30
=255,
(3)设AD=AC=a,BE=BC=b,
则图中阴影部分的面积为(a+b)(a+b)﹣(a +b )
=[(a+b) ﹣(a +b )]
=×2ab
=ab
=10
三.完全平方式
11.解:∵x2﹣6x+k是完全平方式,
∴k=32=9.
故选:B.
12.解:∵x2+8x+m2是一个完全平方式,
∴m2=16,
解得:m=±4.
故选:C.
13.解:∵x2+mx+9=(x±3)2=x2±6x+9,
∴m=±6,
故选:C.
14.解:∵9x2﹣2mx+16是一个完全平方式,
∴﹣m=±12,
∴m=±12.
故选:B.
15.解:∵x2+(k﹣1)x+9是完全平方式,
∴k﹣1=±6,
解得:k=7或﹣5,
故选:D.
四.平方差公式
16.解:A、(x+1)(x﹣1)能用平方差公式计算,故此选项不符合题意;
B、(﹣x+1)(﹣x﹣1)能用平方差公式计算,故此选项不符合题意;
C、(x+1)(﹣x+1)能用平方差公式计算,故此选项不符合题意;
D、(x+1)(1+x)不能用平方差公式计算,故此选项符合题意;
故选:D.
17.解:A、结果是x2﹣y2,原计算正确,故本选项符合题意;
B、结果是x2﹣2xy+y2,原计算错误,故本选项不符合题意;
C、结果是x2+2xy+y2,原计算错误,故本选项不符合题意;
D、结果是y2﹣x2,原计算错误,故本选项不符合题意;
故选:A.
18.解:∵a+b=6,a2﹣b2=30,
∴(a+b)(a﹣b)=30,
∴a﹣b=30÷6=5,
故选:A.
19.解:A、(a+b)(b+a)不能用平方差公式计算,故选项A不符合题意;
B、(﹣m+n)(m﹣n))=﹣(m﹣n)(m﹣n),不能用平方差公式计算,故选项B不符合题意;
C、(2x﹣y)(y+2x)=4x2﹣y2,故选项C符合题意;
D、(x2﹣y)(x+y2)不符合平方差公式,故选项D不符合题意,
故选:C.
20.解:A、两个多项式两项既不相同,也不互为相反数,故此选项不符合题意;
B、两个多项式两项都互为相反数,故选项错误;
C、两个多项式两项都互为相反数,故选项错误;
D、两个多项式两项相同,两项互为相反数,故此选项符合题意.
故选:D.
21.解:(x﹣y+5)(x+y+5)=[(x+5)﹣y][(x+5)+y].
故选:B.
22.解:原式=a2﹣4b2﹣a2+4ab﹣4b2+8b2
=4ab.
23.解:原式=x2+6x+9﹣(x2﹣9)
=x2+6x+9﹣x2+9
=6x+18.
五.平方差公式的几何背景
24.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),
∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),
故选:D.
25.解:图1的面积为:(x+1)(x﹣1),
图2中白色部分的面积为:x2﹣1,
∴(x+1)(x﹣1)=x2﹣1,
故选:B.
26.解:如图①,左图的阴影部分的面积为a2﹣b2,右图的阴影部分是上底为2b,下底为2a,高为(a﹣b)的梯形,因此面积为(2b+2a)(a﹣b)=(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
因此图①方法可以验证平方差公式,
如图②,左图的阴影部分的面积为a2﹣b2,右图的阴影部分是底为(a+b),高为(a﹣b)的平行四边形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
因此图②方法也可以验证平方差公式,
故选:C.
27.解:阴影部分是边长为(a﹣b)的正方形,因此其面积为(a﹣b)2,
阴影部分也可以看作是边长为a的大正方形的面积减去两个长为a,宽为b的长方形面积,再加上边长为b的正方形面积,即a2﹣2ab+b2,
因此有(a﹣b)2=a2﹣2ab+b2,
故选:D.
一.完全平方公式
1.计算(a﹣2b)2=( )
A.a2﹣4ab+4b2 B.a2+4ab+4b2 C.a2﹣4ab﹣4b2 D.a2+4ab﹣4b2
2.下列计算正确的是( )
A.a6÷a2=a3 B.a2+2a=3a3
C.(﹣2ab2)3=﹣8a3b6 D.(2a+b)2=4a2+b2+2ab
3.(1)已知(a+b)2=6,(a﹣b)2=2,求a2+b2与ab的值;
(2)已知a+b=8,a2b2=9,求a2+b2的值.
4.已知(x+y)2=7,(x﹣y)2=5.
(1)求x2+y2值;
(2)求xy的值.
5.已知x=a﹣2021,y=2027﹣a,xy=5.
(1)求x2+y2的值; (2)求(x﹣y)2的值; (3)求a的值.
6.已知(n﹣2020)2+(2021﹣n)2=3,求(n﹣2020)(2021﹣n)的值.
二.完全平方公式的几何背景
7.用4块完全相同的长方形拼成如图所示的正方形,用不同的方法计算图中阴影部分的面积,可得到一个关于a,b的等式为( )
A.4a(a+b)=4a2+4ab B.(a+b)(a﹣b)=a2﹣b2
C.(a+b)2=a2+2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
8.用四个完全一样的长方形(长、宽分别设为a、b,a>b)拼成如图所示大正方形,已知大正方形面积为64,中间空缺的小正方形面积为16,则下列关系式中不正确的是( )
A.a2+b2=64 B.a+b=8 C.a﹣b=4 D.a b=12
9.如图,两个正方形的边长分别为a、b,如果a、b满足a+b=6,ab=8,则阴影部分的面积为( )
A.14 B.12 C.9 D.6
10.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC BC=10,则图中阴影部分的面积为 .
三.完全平方式
11.若x2﹣6x+k是完全平方式,则k的值是( )
A.±9 B.9 C.±12 D.12
12.如果x2+8x+m2是一个完全平方式,那么m的值是( )
A.4 B.16 C.±4 D.±16
13.若x2+mx+9是完全平方式,则m的值为( )
A.6 B.9 C.±6 D.±9
14.若多项式9x2﹣2mx+16是一个完全平方式,则m的值为( )
A.±24 B.±12 C.24 D.12
15.若x2+(k﹣1)x+9是完全平方式,则k的值为( )
A.±6 B.7 C.﹣5 D.7或﹣5
四.平方差公式
16.下列不能用平方差公式运算的是( )
A.(x+1)(x﹣1) B.(﹣x+1)(﹣x﹣1)
C.(x+1)(﹣x+1) D.(x+1)(1+x)
17.下列运算正确的是( )
A.(x+y)(﹣y+x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(y﹣x)=x2﹣y2
18.若a+b=6,a2﹣b2=30,则a﹣b=( )
A.5 B.6 C.10 D.15
19.下列多项式的乘法中,能用平方差公式计算的是( )
A.(a+b)(b+a) B.(﹣m+n)(m﹣n)
C.(2x﹣y)(y+2x) D.(x2﹣y)(x+y2)
20.下列算式能用平方差公式计算的是( )
A.(3a+b)(3b﹣a) B.(x+1)(﹣x﹣1)
C.(2x﹣y)(﹣2x+y) D.(﹣n﹣m)(﹣n+m)
21.如果用平方差公式计算(x﹣y+5)(x+y+5),则可将原式变形为( )
A.[(x﹣y)+5][(x+y)+5] B.[(x+5)﹣y][(x+5)+y]
C.[(x﹣y)+5][(x﹣y)﹣5] D.[x﹣(y+5)][x+(y+5)]
22.化简:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2.
23.计算:(x+3)2﹣(x+3)(x﹣3).
五.平方差公式的几何背景
24.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是( )
A.a2+b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
25.如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式( )
A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1
C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x
26.如图,阴影部分是在边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形.给出下列2种割拼方法,其中能够验证平方差公式的是( )
A.① B.② C.①② D.①②都不能
27.如图,用不同的代数式表示图中阴影部分的面积,可得等式( )
A.(a+b)2=a2+2ab+b2 B.(a﹣b)2=a2+2ab﹣b2
C.(a+b)(a﹣b)=a2﹣b2 D.(a﹣b)2=a2﹣2ab+b2
参考答案
一.完全平方公式
1.解:原式=a2﹣2a 2b+(2b)2
=a2﹣4ab+4b2,
故选:A.
2.解:A.a6÷a2=a4,原说法错误,故选项不符合题意;
B.a2和2a不能合并,,原说法错误,故选项不符合题意;
C.(﹣2ab2)3=﹣8a3b6,正确,故选项符合题意;
D.(2a+b)2=4a2+b2+4ab,原说法错误,故选项不符合题意;
故选:C.
3.解:(1)∵(a+b)2=6,(a﹣b)2=2,
∴a2+2ab+b2=6①,a2﹣2ab+b2=2②,
∴①+②得:
a2+2ab+b2+a2﹣2ab+b2=8,
则a2+b2=4;
①﹣②得:
4ab=4,
则ab=1;
(2)∵a+b=8,a2b2=9,
∴(a+b)2=64,ab=±3,
∴a2+2ab+b2=64,
∴a2+b2=64﹣2ab=64﹣2×3=58,或a2+b2=64﹣2ab=64﹣2×(﹣3)=70,
即a2+b2的值是58或70.
4.解:(1)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①+②得:
x2+2xy+y2+x2﹣2xy+y2=12,
则x2+y2=6;
(2)∵(x+y)2=7,(x﹣y)2=5,
∴x2+2xy+y2=7①,x2﹣2xy+y2=5②,
∴①﹣②得:
4xy=2,
解得:xy=.
5.解:(1)∵x=a﹣2021,y=2027﹣a,xy=5,
∴x+y=a﹣2021+2027﹣a=6.
∴x2+y2=(x+y)2﹣2xy=62﹣2×5=36﹣10=26.
(2)由(1)知:x2+y2=26.
∴(x﹣y)2=x2+y2﹣2xy=26﹣2×5=16.
(3)由(2)知:(x﹣y)2=16.
∴x﹣y=4或x﹣y=﹣4.
当x﹣y=4时,由x+y=6,解得x=5,y=1,此时a=x+2021=2026.
当x﹣y=﹣4时,由x+y=6,解得x=1,y=5,此时a=x+2021=2022.
综上:a=2026或a=2022.
6.解:令n﹣2020=a,2021﹣n=b,
根据题意得:
a2+b2=3,a+b=1,
∴原式=ab
=
=
=﹣1.
二.完全平方公式的几何背景
7.解:∵图形中大正方形的面积为(a+b)2,
中间空白正方形的面积为(a﹣b)2,
∴图中阴影部分的面积为(a+b)2﹣(a﹣b)2,
又∵图中阴影部分的面积还可表示为4ab,
∴(a+b)2﹣(a﹣b)2=4ab,
故选:D.
8.解:∵大正方形的面积为64,中间空缺的小正方形的面积为16,
∴大正方形的边长为8,小正方形的边长为4,
即:a+b=8,a﹣b=4,
因此a=6,b=2,
∴a2+b2=36+4=40,ab=6×2=12,
故选:A.
9.解:由各个部分面积之间的关系可得,
S阴影部分=S正方形ABCD+S正方形AEFG﹣S△BCD﹣S△BEF
=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab]
=(62﹣3×8)
=6,
故选:D.
10.(1)∵a2+b2=8,(a+b)2=48,
∴ab===20,
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)] ﹣2(25﹣x)(x﹣10)
=15 ﹣2×(﹣15)
=225+30
=255,
(3)设AD=AC=a,BE=BC=b,
则图中阴影部分的面积为(a+b)(a+b)﹣(a +b )
=[(a+b) ﹣(a +b )]
=×2ab
=ab
=10
三.完全平方式
11.解:∵x2﹣6x+k是完全平方式,
∴k=32=9.
故选:B.
12.解:∵x2+8x+m2是一个完全平方式,
∴m2=16,
解得:m=±4.
故选:C.
13.解:∵x2+mx+9=(x±3)2=x2±6x+9,
∴m=±6,
故选:C.
14.解:∵9x2﹣2mx+16是一个完全平方式,
∴﹣m=±12,
∴m=±12.
故选:B.
15.解:∵x2+(k﹣1)x+9是完全平方式,
∴k﹣1=±6,
解得:k=7或﹣5,
故选:D.
四.平方差公式
16.解:A、(x+1)(x﹣1)能用平方差公式计算,故此选项不符合题意;
B、(﹣x+1)(﹣x﹣1)能用平方差公式计算,故此选项不符合题意;
C、(x+1)(﹣x+1)能用平方差公式计算,故此选项不符合题意;
D、(x+1)(1+x)不能用平方差公式计算,故此选项符合题意;
故选:D.
17.解:A、结果是x2﹣y2,原计算正确,故本选项符合题意;
B、结果是x2﹣2xy+y2,原计算错误,故本选项不符合题意;
C、结果是x2+2xy+y2,原计算错误,故本选项不符合题意;
D、结果是y2﹣x2,原计算错误,故本选项不符合题意;
故选:A.
18.解:∵a+b=6,a2﹣b2=30,
∴(a+b)(a﹣b)=30,
∴a﹣b=30÷6=5,
故选:A.
19.解:A、(a+b)(b+a)不能用平方差公式计算,故选项A不符合题意;
B、(﹣m+n)(m﹣n))=﹣(m﹣n)(m﹣n),不能用平方差公式计算,故选项B不符合题意;
C、(2x﹣y)(y+2x)=4x2﹣y2,故选项C符合题意;
D、(x2﹣y)(x+y2)不符合平方差公式,故选项D不符合题意,
故选:C.
20.解:A、两个多项式两项既不相同,也不互为相反数,故此选项不符合题意;
B、两个多项式两项都互为相反数,故选项错误;
C、两个多项式两项都互为相反数,故选项错误;
D、两个多项式两项相同,两项互为相反数,故此选项符合题意.
故选:D.
21.解:(x﹣y+5)(x+y+5)=[(x+5)﹣y][(x+5)+y].
故选:B.
22.解:原式=a2﹣4b2﹣a2+4ab﹣4b2+8b2
=4ab.
23.解:原式=x2+6x+9﹣(x2﹣9)
=x2+6x+9﹣x2+9
=6x+18.
五.平方差公式的几何背景
24.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),
∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),
故选:D.
25.解:图1的面积为:(x+1)(x﹣1),
图2中白色部分的面积为:x2﹣1,
∴(x+1)(x﹣1)=x2﹣1,
故选:B.
26.解:如图①,左图的阴影部分的面积为a2﹣b2,右图的阴影部分是上底为2b,下底为2a,高为(a﹣b)的梯形,因此面积为(2b+2a)(a﹣b)=(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
因此图①方法可以验证平方差公式,
如图②,左图的阴影部分的面积为a2﹣b2,右图的阴影部分是底为(a+b),高为(a﹣b)的平行四边形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
因此图②方法也可以验证平方差公式,
故选:C.
27.解:阴影部分是边长为(a﹣b)的正方形,因此其面积为(a﹣b)2,
阴影部分也可以看作是边长为a的大正方形的面积减去两个长为a,宽为b的长方形面积,再加上边长为b的正方形面积,即a2﹣2ab+b2,
因此有(a﹣b)2=a2﹣2ab+b2,
故选:D.
