24.2.1点和圆的位置关系 同步练习题 2021-2022学年人教版数学九年级上册(Word版含答案)
文档属性
| 名称 | 24.2.1点和圆的位置关系 同步练习题 2021-2022学年人教版数学九年级上册(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 336.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学上册《24.2.1点和圆的位置关系》同步练习题(附答案)
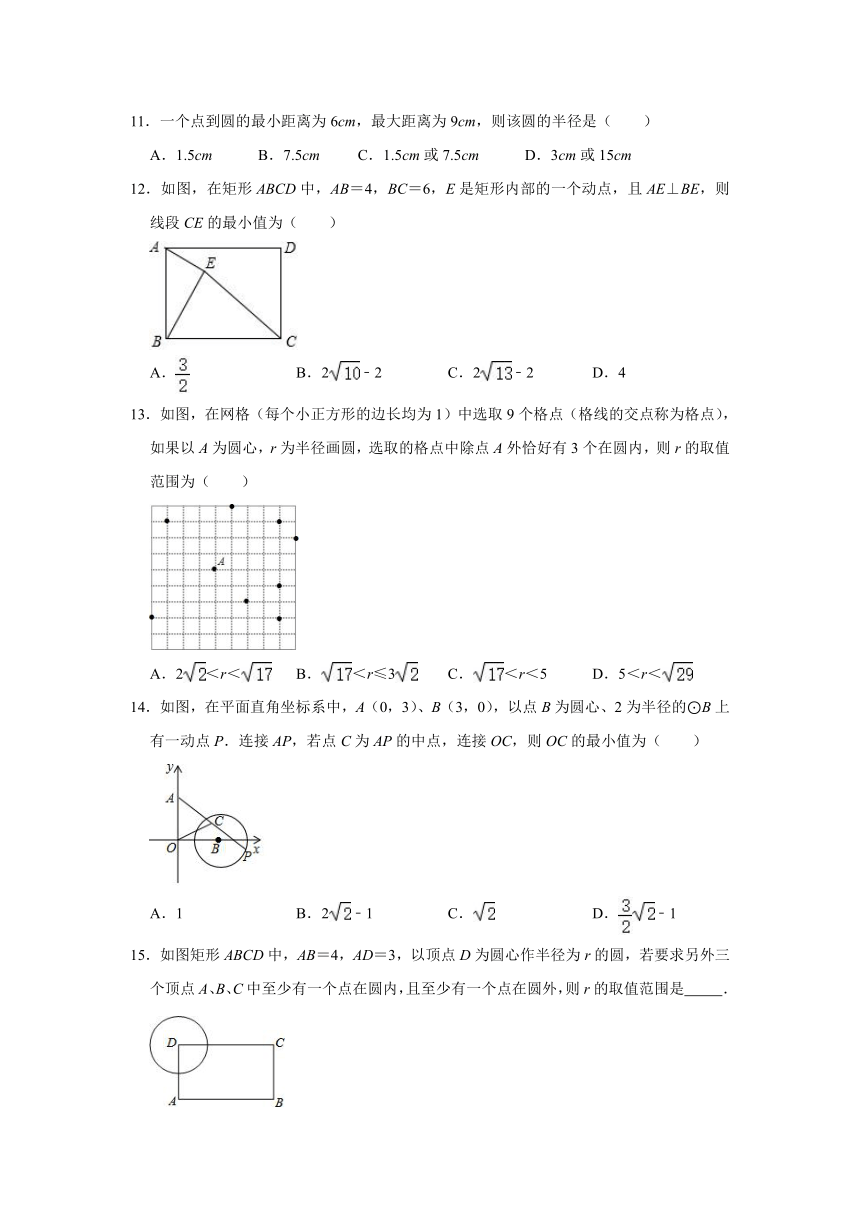
1.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.2 C. D.
2.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
3.一个点到圆的最小距离为3cm,最大距离为8cm,则该圆的半径是( )
A.5cm或11cm B.2.5cm
C.5.5cm D.2.5cm或5.5cm
4.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
5.如图,在平面直角坐标系中,C(0,4),A(3,0),⊙A半径为2,P为⊙A上任意一点,E是PC的中点,则OE的最小值是( )
A.1 B. C.2 D.
6.在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A. B. C.34 D.10
7.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P的⊙O上
C.点P在⊙O外 D.点P在⊙O上或⊙O外
8.如图,AB是半圆O的直径,点D在半圆O上,AB=2,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
9.⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.可能在⊙O上或在⊙O内
10.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1 B.+ C.2+1 D.2﹣
11.一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是( )
A.1.5cm B.7.5cm C.1.5cm或7.5cm D.3cm或15cm
12.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
A. B.2﹣2 C.2﹣2 D.4
13.如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A.2<r< B.<r≤3 C.<r<5 D.5<r<
14.如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A.1 B.2﹣1 C. D.﹣1
15.如图矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
16.在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连接PA,PB.若PB=4,则PA的长为 .
17.如图,在平面直角坐标系中,点P是以C(﹣,)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是 .
18.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过 秒后,点P在⊙O上.
19.如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
20.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
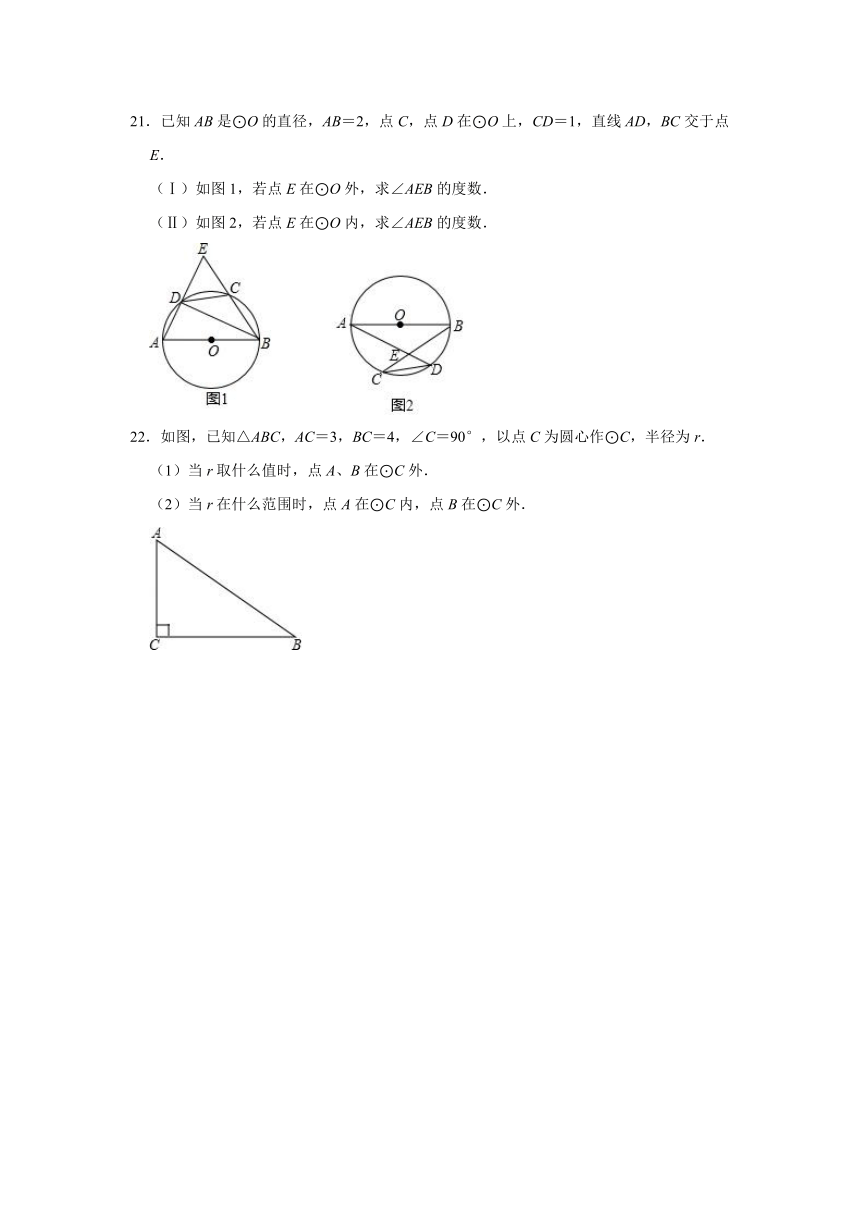
21.已知AB是⊙O的直径,AB=2,点C,点D在⊙O上,CD=1,直线AD,BC交于点E.
(Ⅰ)如图1,若点E在⊙O外,求∠AEB的度数.
(Ⅱ)如图2,若点E在⊙O内,求∠AEB的度数.
22.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
参考答案
1.解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴OP=OA=OB(直角三角形斜边中线等于斜边一半),
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC==5,
∴PC=OC﹣OP=5﹣3=2.
∴PC最小值为2.
故选:B.
2.解:∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6,
故选:C.
3.解:当点P在圆内时,最近点的距离为3cm,最远点的距离为8cm,则直径是11cm,因而半径是5.5cm;
当点P在圆外时,最近点的距离为3cm,最远点的距离为8m,则直径是5cm,因而半径是2.5cm.
故选:D.
4.解:∵⊙O的半径为5cm,点A到圆心O的距离为3cm,
即点A到圆心O的距离小于圆的半径,
∴点A在⊙O内.
故选:B.
5.解:如图,连接AC,取AC的中点H,连接EH,OH.
∵CE=EP,CH=AH,
∴EH=PA=1,
∴点E的运动轨迹是以H为圆心半径为1的圆,
∵C(0,4),A(3,0),
∴H(1.5,2),
∴OH==2.5,
∴OE的最小值=OH﹣EH=2.5﹣1=1.5,
故选:B.
6.解:设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.
∵DE=4,四边形DEFG为矩形,
∴GF=DE,MN=EF,
∴MP=FN=DE=2,
∴NP=MN﹣MP=EF﹣MP=1,
∴PF2+PG2=2PN2+2FN2=2×12+2×22=10.
故选:D.
7.解:∵圆心O的坐标为(0,0),点P的坐标为(4,2),
∴OP==<5,因而点P在⊙O内.
故选:A.
8.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
9.解:由题意可知△OPM为直角三角形,且PM=3,OM=4,
由勾股定理可求得OP=5=r,
故点P在⊙O上,
故选:B.
10.解:如图,
∵点C为坐标平面内一点,BC=1,
∴C在⊙B上,且半径为1,
取OD=OA=2,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=2,∠BOD=90°,
∴BD=2,
∴CD=2+1,
∴OM=CD=,即OM的最大值为+;
故选:B.
11.解:分为两种情况:
①当点P在圆内时,最近点的距离为6cm,最远点的距离为9cm,则直径是15cm,因而半径是7.5cm;
②当点P在圆外时,最近点的距离为6cm,最远点的距离为9cm,则直径是3cm,因而半径是1.5cm.
故选:C.
12.解:如图,
∵AE⊥BE,
∴点E在以AB为直径的半⊙O上,
连接CO交⊙O于点E′,
∴当点E位于点E′位置时,线段CE取得最小值,
∵AB=4,
∴OA=OB=OE′=2,
∵BC=6,
∴OC===2,
则CE′=OC﹣OE′=2﹣2,
故选:B.
13.解:给各点标上字母,如图所示.
AB==2,AC=AD==,AE==3,AF==,AG=AM=AN==5,
∴<r≤3时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
故选:B.
14.解:当点P运动到AB的延长线上时,即如图中点P1,C1是AP1的中点,
当点P在线段AB上时,C2是中点,取C1C2的中点为D,
点C的运动路径是以D为圆心,以DC1为半径的圆(CA:PA=1:2,则点C轨迹和点P轨迹相似,所以点C的轨迹就是圆),当O、C、D共线时,OC的长最小,
设线段AB交⊙B于Q,
Rt△AOB中,OA=3,OB=3,
∴AB=3,
∵⊙B的半径为2,
∴BP1=2,AP1=3+2,
∵C1是AP1的中点,
∴AC1=+1,AQ=3﹣2,
∵C2是AQ的中点,
∴AC2=C2Q=﹣1,
C1C2=+1﹣(﹣1)=2,即⊙D的半径为1,
∵AD=﹣1+1==AB,
∴OD=AB=,
∴OC=﹣1,
方法二:如图,取A′(0,﹣3),连接PA′.
根据三角形中位线定理可知:PA′=2OC,求出PA′的最小值即可解决问题.
故选:D.
15.解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
故答案为:3<r<5.
16.解:连接CP,PB的延长线交⊙C于P′,如图,
∵CP=5,CB=3,PB=4,
∴CB2+PB2=CP2,
∴△CPB为直角三角形,∠CBP=90°,
∴CB⊥PB,
∴PB=P′B=4,
∵∠C=90°,
∴PB∥AC,
而PB=AC=4,
∴四边形ACBP为矩形,
∴PA=BC=3,
在Rt△APP′中,∵PA=3,PP′=8,
∴P′A==,
∴PA的长为3或.
故答案为3或.
17.解:设P(x,y),
∵PA2=(x+1)2+y2,PB2=(x﹣1)2+y2,
∴PA2+PB2=2x2+2y2+2=2(x2+y2)+2,
∵OP2=x2+y2,
∴PA2+PB2=2OP2+2,
当点P处于OC与圆的交点上时,OP取得最值,
∴OP的最小值为CO﹣CP=﹣1,
∴PA2+PB2最小值为14﹣4.
故答案为:14﹣4.
18.解:设x秒后点P在圆O上,
∵原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,
∴当第一次点P在圆上时,
(2+1)x=7﹣1=6
解得:x=2;
当第二次点P在圆上时,
(2+1)x=7+1=8
解得:x=
答案为:2或;
19.解:设OA交⊙O于C,连接B′C,如图2,
∵OA′ OA=42,
而r=4,OA=8,
∴OA′=2,
∵OB′ OB=42,
∴OB′=4,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′=,
∴A′B′=2.
20.解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE==,P2E=1,
∴AP2=﹣1.
21.解:(Ⅰ)如图1,连接OC、OD,
∵CD=1,OC=OD=1,
∴△OCD为等边三角形,
∴∠COD=60°,
∴∠CBD=∠COD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠AEB=90°﹣∠DBE=90°﹣30°=60°;
(Ⅱ)如图2,连接OC、OD,同理可得∠CBD=30°,∠ADB=90°,
∴∠AEB=90°+∠DBE=90°+30°=120°.
22.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
1.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.2 C. D.
2.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
3.一个点到圆的最小距离为3cm,最大距离为8cm,则该圆的半径是( )
A.5cm或11cm B.2.5cm
C.5.5cm D.2.5cm或5.5cm
4.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
5.如图,在平面直角坐标系中,C(0,4),A(3,0),⊙A半径为2,P为⊙A上任意一点,E是PC的中点,则OE的最小值是( )
A.1 B. C.2 D.
6.在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A. B. C.34 D.10
7.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P的⊙O上
C.点P在⊙O外 D.点P在⊙O上或⊙O外
8.如图,AB是半圆O的直径,点D在半圆O上,AB=2,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
9.⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P( )
A.在⊙O内 B.在⊙O上
C.在⊙O外 D.可能在⊙O上或在⊙O内
10.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1 B.+ C.2+1 D.2﹣
11.一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是( )
A.1.5cm B.7.5cm C.1.5cm或7.5cm D.3cm或15cm
12.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
A. B.2﹣2 C.2﹣2 D.4
13.如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A.2<r< B.<r≤3 C.<r<5 D.5<r<
14.如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A.1 B.2﹣1 C. D.﹣1
15.如图矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
16.在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连接PA,PB.若PB=4,则PA的长为 .
17.如图,在平面直角坐标系中,点P是以C(﹣,)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是 .
18.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过 秒后,点P在⊙O上.
19.如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
20.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
21.已知AB是⊙O的直径,AB=2,点C,点D在⊙O上,CD=1,直线AD,BC交于点E.
(Ⅰ)如图1,若点E在⊙O外,求∠AEB的度数.
(Ⅱ)如图2,若点E在⊙O内,求∠AEB的度数.
22.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
参考答案
1.解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴OP=OA=OB(直角三角形斜边中线等于斜边一半),
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC==5,
∴PC=OC﹣OP=5﹣3=2.
∴PC最小值为2.
故选:B.
2.解:∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6,
故选:C.
3.解:当点P在圆内时,最近点的距离为3cm,最远点的距离为8cm,则直径是11cm,因而半径是5.5cm;
当点P在圆外时,最近点的距离为3cm,最远点的距离为8m,则直径是5cm,因而半径是2.5cm.
故选:D.
4.解:∵⊙O的半径为5cm,点A到圆心O的距离为3cm,
即点A到圆心O的距离小于圆的半径,
∴点A在⊙O内.
故选:B.
5.解:如图,连接AC,取AC的中点H,连接EH,OH.
∵CE=EP,CH=AH,
∴EH=PA=1,
∴点E的运动轨迹是以H为圆心半径为1的圆,
∵C(0,4),A(3,0),
∴H(1.5,2),
∴OH==2.5,
∴OE的最小值=OH﹣EH=2.5﹣1=1.5,
故选:B.
6.解:设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.
∵DE=4,四边形DEFG为矩形,
∴GF=DE,MN=EF,
∴MP=FN=DE=2,
∴NP=MN﹣MP=EF﹣MP=1,
∴PF2+PG2=2PN2+2FN2=2×12+2×22=10.
故选:D.
7.解:∵圆心O的坐标为(0,0),点P的坐标为(4,2),
∴OP==<5,因而点P在⊙O内.
故选:A.
8.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
9.解:由题意可知△OPM为直角三角形,且PM=3,OM=4,
由勾股定理可求得OP=5=r,
故点P在⊙O上,
故选:B.
10.解:如图,
∵点C为坐标平面内一点,BC=1,
∴C在⊙B上,且半径为1,
取OD=OA=2,连接CD,
∵AM=CM,OD=OA,
∴OM是△ACD的中位线,
∴OM=CD,
当OM最大时,即CD最大,而D,B,C三点共线时,当C在DB的延长线上时,OM最大,
∵OB=OD=2,∠BOD=90°,
∴BD=2,
∴CD=2+1,
∴OM=CD=,即OM的最大值为+;
故选:B.
11.解:分为两种情况:
①当点P在圆内时,最近点的距离为6cm,最远点的距离为9cm,则直径是15cm,因而半径是7.5cm;
②当点P在圆外时,最近点的距离为6cm,最远点的距离为9cm,则直径是3cm,因而半径是1.5cm.
故选:C.
12.解:如图,
∵AE⊥BE,
∴点E在以AB为直径的半⊙O上,
连接CO交⊙O于点E′,
∴当点E位于点E′位置时,线段CE取得最小值,
∵AB=4,
∴OA=OB=OE′=2,
∵BC=6,
∴OC===2,
则CE′=OC﹣OE′=2﹣2,
故选:B.
13.解:给各点标上字母,如图所示.
AB==2,AC=AD==,AE==3,AF==,AG=AM=AN==5,
∴<r≤3时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
故选:B.
14.解:当点P运动到AB的延长线上时,即如图中点P1,C1是AP1的中点,
当点P在线段AB上时,C2是中点,取C1C2的中点为D,
点C的运动路径是以D为圆心,以DC1为半径的圆(CA:PA=1:2,则点C轨迹和点P轨迹相似,所以点C的轨迹就是圆),当O、C、D共线时,OC的长最小,
设线段AB交⊙B于Q,
Rt△AOB中,OA=3,OB=3,
∴AB=3,
∵⊙B的半径为2,
∴BP1=2,AP1=3+2,
∵C1是AP1的中点,
∴AC1=+1,AQ=3﹣2,
∵C2是AQ的中点,
∴AC2=C2Q=﹣1,
C1C2=+1﹣(﹣1)=2,即⊙D的半径为1,
∵AD=﹣1+1==AB,
∴OD=AB=,
∴OC=﹣1,
方法二:如图,取A′(0,﹣3),连接PA′.
根据三角形中位线定理可知:PA′=2OC,求出PA′的最小值即可解决问题.
故选:D.
15.解:在直角△ABD中,CD=AB=4,AD=3,
则BD==5.
由图可知3<r<5.
故答案为:3<r<5.
16.解:连接CP,PB的延长线交⊙C于P′,如图,
∵CP=5,CB=3,PB=4,
∴CB2+PB2=CP2,
∴△CPB为直角三角形,∠CBP=90°,
∴CB⊥PB,
∴PB=P′B=4,
∵∠C=90°,
∴PB∥AC,
而PB=AC=4,
∴四边形ACBP为矩形,
∴PA=BC=3,
在Rt△APP′中,∵PA=3,PP′=8,
∴P′A==,
∴PA的长为3或.
故答案为3或.
17.解:设P(x,y),
∵PA2=(x+1)2+y2,PB2=(x﹣1)2+y2,
∴PA2+PB2=2x2+2y2+2=2(x2+y2)+2,
∵OP2=x2+y2,
∴PA2+PB2=2OP2+2,
当点P处于OC与圆的交点上时,OP取得最值,
∴OP的最小值为CO﹣CP=﹣1,
∴PA2+PB2最小值为14﹣4.
故答案为:14﹣4.
18.解:设x秒后点P在圆O上,
∵原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,
∴当第一次点P在圆上时,
(2+1)x=7﹣1=6
解得:x=2;
当第二次点P在圆上时,
(2+1)x=7+1=8
解得:x=
答案为:2或;
19.解:设OA交⊙O于C,连接B′C,如图2,
∵OA′ OA=42,
而r=4,OA=8,
∴OA′=2,
∵OB′ OB=42,
∴OB′=4,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′=,
∴A′B′=2.
20.解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE==,P2E=1,
∴AP2=﹣1.
21.解:(Ⅰ)如图1,连接OC、OD,
∵CD=1,OC=OD=1,
∴△OCD为等边三角形,
∴∠COD=60°,
∴∠CBD=∠COD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠AEB=90°﹣∠DBE=90°﹣30°=60°;
(Ⅱ)如图2,连接OC、OD,同理可得∠CBD=30°,∠ADB=90°,
∴∠AEB=90°+∠DBE=90°+30°=120°.
22.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
同课章节目录
