2021-2022学年高一上学期数学苏教版(2019)必修第一册5.3函数的单调性课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学苏教版(2019)必修第一册5.3函数的单调性课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 909.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 09:26:16 | ||
图片预览




文档简介
(共17张PPT)
5.2.3 函数的单调性
学习目标
1.理解函数的单调性,能运用函数图象理解和研究函数的单调性.
2.会用函数单调性的定义判断(或证明)一些函数的单调性.(重难点)
3.会求一些具体函数的单调区间.(重难点)
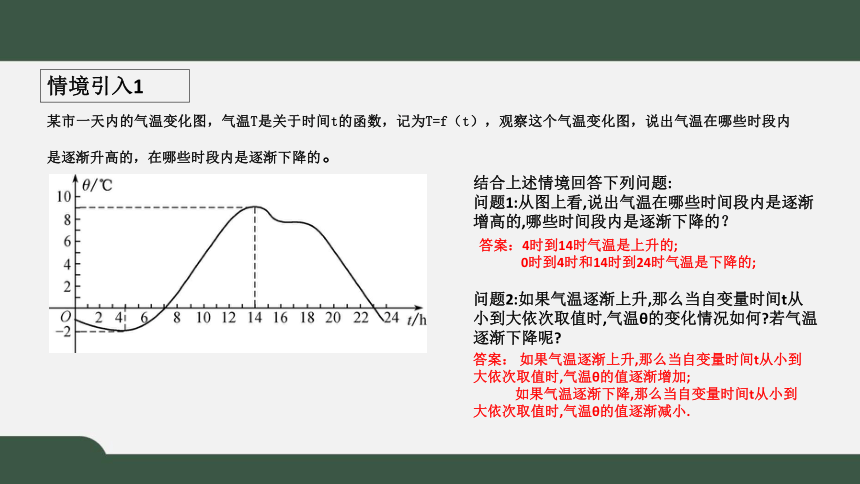
某市一天内的气温变化图,气温T是关于时间t的函数,记为T=f(t),观察这个气温变化图,说出气温在哪些时段内是逐渐升高的,在哪些时段内是逐渐下降的。
情境引入1
结合上述情境回答下列问题:
问题1:从图上看,说出气温在哪些时间段内是逐渐增高的,哪些时间段内是逐渐下降的?
问题2:如果气温逐渐上升,那么当自变量时间t从小到大依次取值时,气温θ的变化情况如何 若气温逐渐下降呢
答案:4时到14时气温是上升的;
0时到4时和14时到24时气温是下降的;
答案: 如果气温逐渐上升,那么当自变量时间t从小到大依次取值时,气温θ的值逐渐增加;
如果气温逐渐下降,那么当自变量时间t从小到大依次取值时,气温θ的值逐渐减小.
函数f(x)=x,g(x)= 的图象如图,观察其变化规律,回答下列问题.
图1 图2
问题1:从图1上看,自变量x增大时,函数f(x)的值如何变化
问题2:从图2上看,自变量x增大时,函数g(x)的值如何变化
问题3:如果一个函数的图象从左至右逐渐上升,那么当自变量x从小到大依次取值时,函数值y的变化情况如何
情境引入2
答案
问题1:图1中,自变量x增大时,函数f(x)的值也在增大.
问题2:图2中,在y轴左侧,自变量x增大时,函数g(x)的值在减小;在y轴右侧,自变量x增大时,函数g(x)的值也在增大.
问题3:如果一个函数的图象从左至右逐渐上升,对应的当x从小到大依次取值时,函数值y依次增大.
答案解析:
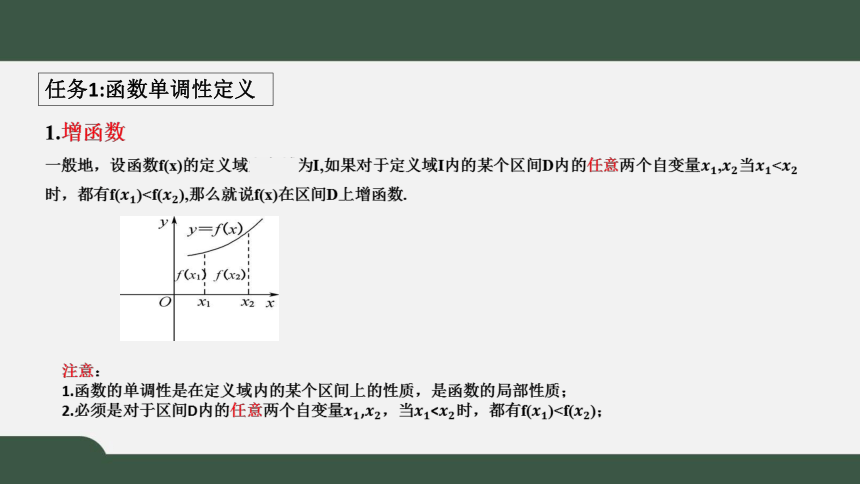
任务1:函数单调性定义
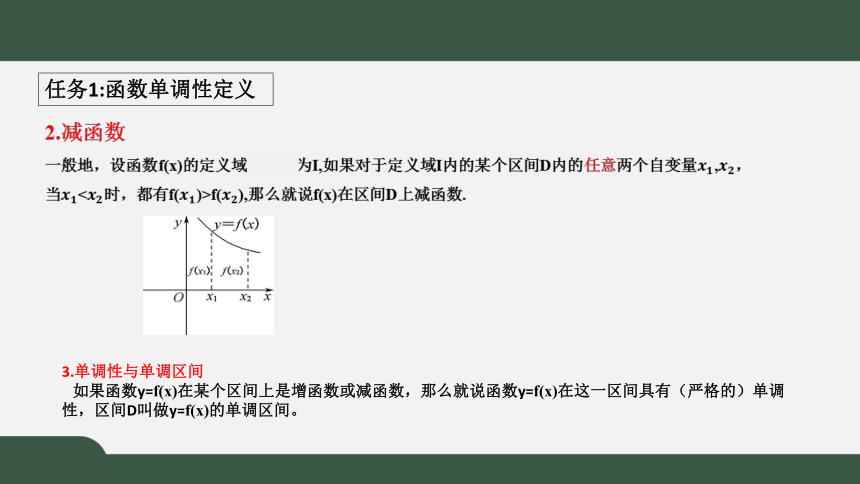
任务1:函数单调性定义
3.单调性与单调区间
如果函数y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间。
思考讨论:
请根据图像简单叙述一下函数图像的单调区间,单调递增区间?或者单调递减区间?
类型1 利用函数图象求单调区间
注意事项:
方法指导 由函数图象确定函数单调性的方法及注意事项
(1)图象从左向右上升,则函数递增;图象从左向右下降,则函数递减.
(2)单调区间必须是函数定义域的子集,单调区间之间不能用“∪”,而应用“,”将它们隔开或用“和”字连接.
类型2 函数单调性的判定与证明
训练2 判断或证明函数的单调性
(1)求f(x)的定义域;
(2)判断函数f(x)在(1,+∞)上单调性,并用定义加以证明.
解 (1)由x2-1≠0,得x≠±1,
证明: x1,x2∈(1,+∞),且x10,
由x1,x2∈(1,+∞),得x1>1,x2>1,
又x1即f(x1)>f(x2),
课堂小结:
1.函数单调性定义
2.利用函数图象求单调区间
3.函数单调性的判定与证明
课后作业:
完成课后作业与金太阳导学案
谢 谢 观 看
5.2.3 函数的单调性
学习目标
1.理解函数的单调性,能运用函数图象理解和研究函数的单调性.
2.会用函数单调性的定义判断(或证明)一些函数的单调性.(重难点)
3.会求一些具体函数的单调区间.(重难点)
某市一天内的气温变化图,气温T是关于时间t的函数,记为T=f(t),观察这个气温变化图,说出气温在哪些时段内是逐渐升高的,在哪些时段内是逐渐下降的。
情境引入1
结合上述情境回答下列问题:
问题1:从图上看,说出气温在哪些时间段内是逐渐增高的,哪些时间段内是逐渐下降的?
问题2:如果气温逐渐上升,那么当自变量时间t从小到大依次取值时,气温θ的变化情况如何 若气温逐渐下降呢
答案:4时到14时气温是上升的;
0时到4时和14时到24时气温是下降的;
答案: 如果气温逐渐上升,那么当自变量时间t从小到大依次取值时,气温θ的值逐渐增加;
如果气温逐渐下降,那么当自变量时间t从小到大依次取值时,气温θ的值逐渐减小.
函数f(x)=x,g(x)= 的图象如图,观察其变化规律,回答下列问题.
图1 图2
问题1:从图1上看,自变量x增大时,函数f(x)的值如何变化
问题2:从图2上看,自变量x增大时,函数g(x)的值如何变化
问题3:如果一个函数的图象从左至右逐渐上升,那么当自变量x从小到大依次取值时,函数值y的变化情况如何
情境引入2
答案
问题1:图1中,自变量x增大时,函数f(x)的值也在增大.
问题2:图2中,在y轴左侧,自变量x增大时,函数g(x)的值在减小;在y轴右侧,自变量x增大时,函数g(x)的值也在增大.
问题3:如果一个函数的图象从左至右逐渐上升,对应的当x从小到大依次取值时,函数值y依次增大.
答案解析:
任务1:函数单调性定义
任务1:函数单调性定义
3.单调性与单调区间
如果函数y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间。
思考讨论:
请根据图像简单叙述一下函数图像的单调区间,单调递增区间?或者单调递减区间?
类型1 利用函数图象求单调区间
注意事项:
方法指导 由函数图象确定函数单调性的方法及注意事项
(1)图象从左向右上升,则函数递增;图象从左向右下降,则函数递减.
(2)单调区间必须是函数定义域的子集,单调区间之间不能用“∪”,而应用“,”将它们隔开或用“和”字连接.
类型2 函数单调性的判定与证明
训练2 判断或证明函数的单调性
(1)求f(x)的定义域;
(2)判断函数f(x)在(1,+∞)上单调性,并用定义加以证明.
解 (1)由x2-1≠0,得x≠±1,
证明: x1,x2∈(1,+∞),且x1
由x1,x2∈(1,+∞),得x1>1,x2>1,
又x1
课堂小结:
1.函数单调性定义
2.利用函数图象求单调区间
3.函数单调性的判定与证明
课后作业:
完成课后作业与金太阳导学案
谢 谢 观 看
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
