2021-2022学年数学苏教版(2019)选择性必修第一册1.2.1直线的方程(1)——点斜式、斜截式(1)课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年数学苏教版(2019)选择性必修第一册1.2.1直线的方程(1)——点斜式、斜截式(1)课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 896.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 09:27:58 | ||
图片预览



文档简介
(共22张PPT)
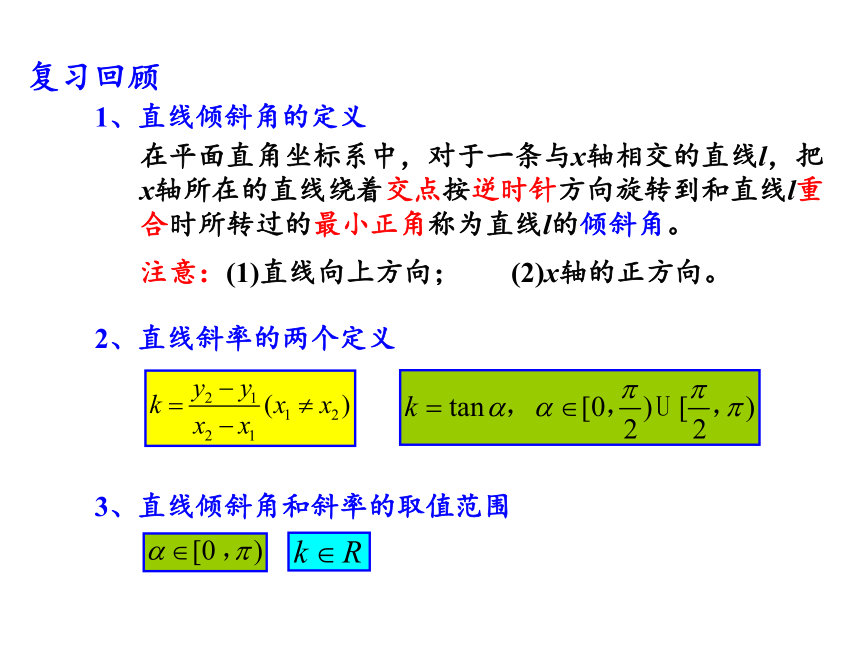
2、直线斜率的两个定义
3、直线倾斜角和斜率的取值范围
1、直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
注意:(1)直线向上方向; (2)x轴的正方向。
复习回顾
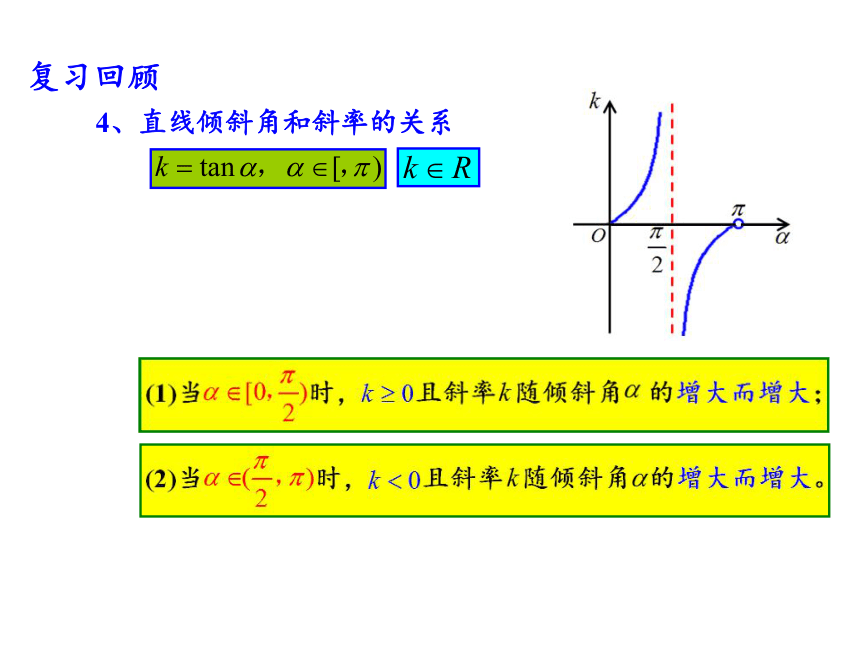
4、直线倾斜角和斜率的关系
复习回顾
情境导入
飞逝的流星形成了一条美丽的弧线,这条弧线可以看做是满足某种运动规律的点的集合;在平面直角坐标系中,直线也可以看做是满足某种条件的点的集合,直线的位置既可由两点唯一确定,也可由一点和一个方向来确定。
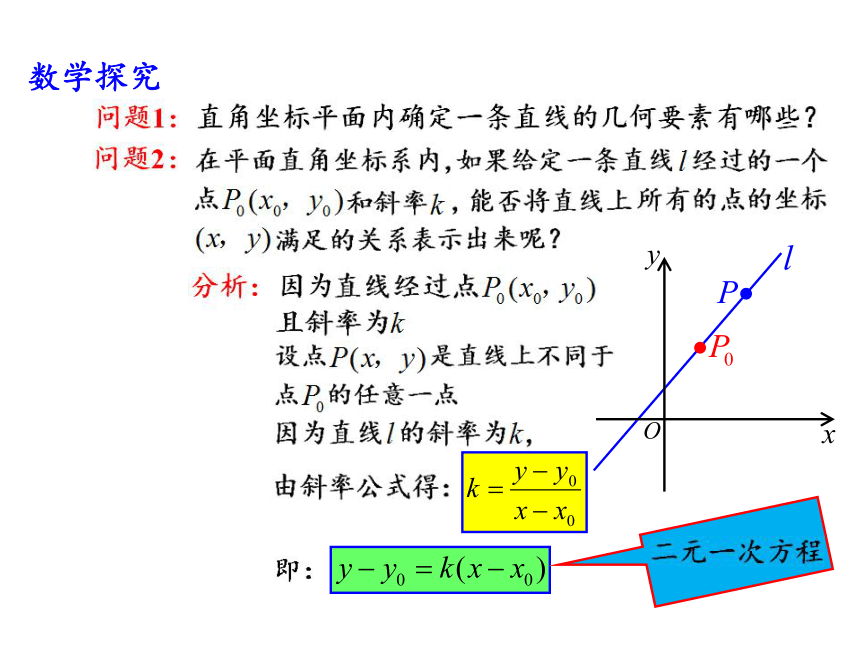
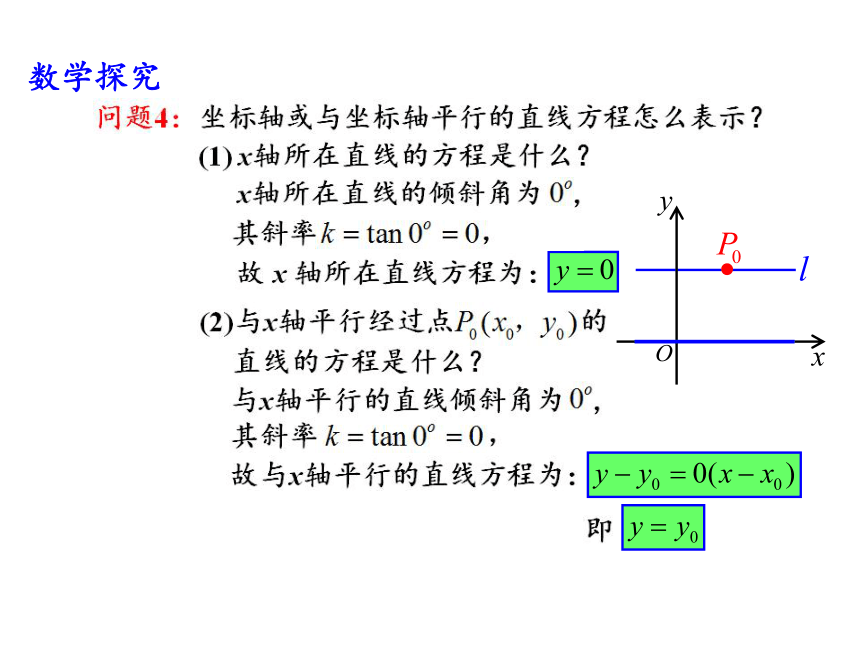
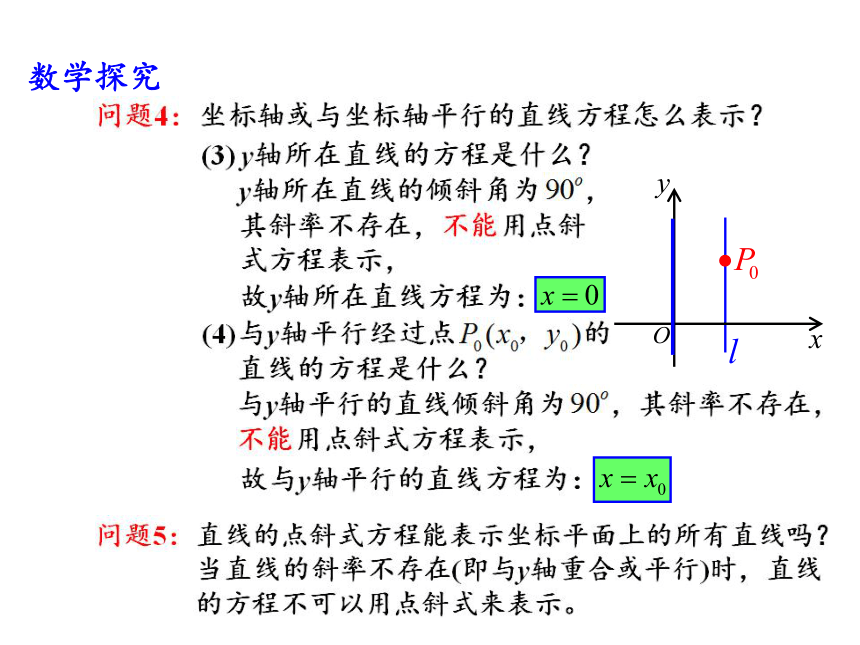
数学探究
数学探究
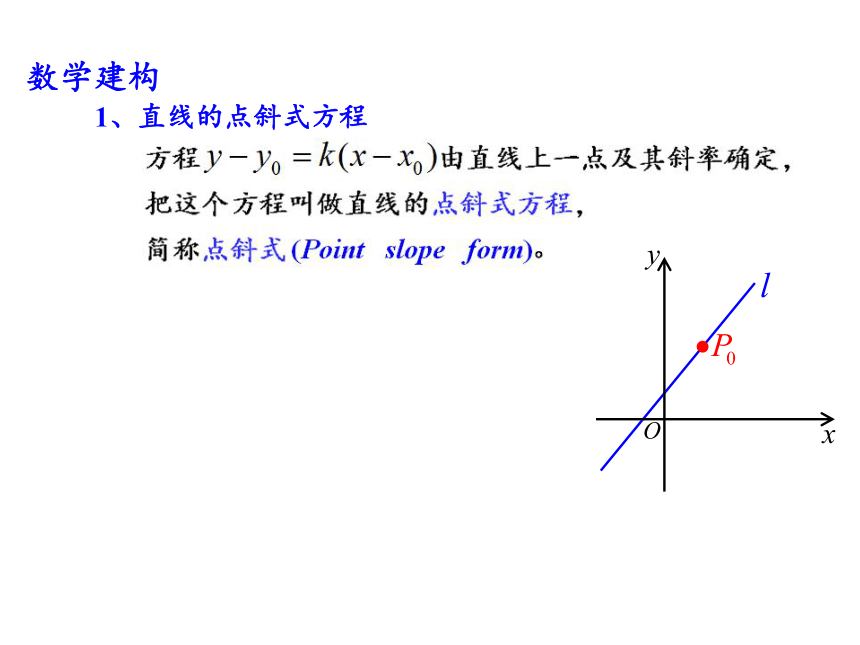
数学建构
1、直线的点斜式方程
数学探究
数学探究
数学应用
类型一 利用点斜式、斜截式求直线方程
例1、求下列直线的点斜式方程
(1)直线经过点P(-2,3),斜率为2;
(2)直线经过点A (-1,2),且倾斜角α=135o;
(3)直线的斜率为2,经过点(0,1)。
变式拓展
已知直线的斜率为k,与y轴的交点是P(0,b),求这条直线的方程。
数学建构
2、直线的斜截式方程
数学探究
数学探究
问题8:斜截式与点斜式存在什么关系?
斜截式是点斜式的特殊情况,有时比点斜式更方便
问题9:斜截式y=kx+b在形式上与一次函数的表达式一样,
它们之间有什么差别?
只有当k≠0时,斜截式方程才是一次函数的表达式
数学练习
1、直线3x+2y-6=0的斜率为______ ,纵截距为_______
2、若直线的斜率是 ,在y 轴上的截距是-2,则直线的
方程为___________,若直线的倾斜角为135o,在y轴
上的截距为0,则直线的方程为___________
数学应用
例2、若直线l经过点A(-1,-3),其倾斜角等于直线
的倾斜角的2倍,求直线 l的方程。
数学应用
例3、已知△ABC的顶点为A(-1,2),B(-3,2),又AC的斜
率为 ,求直线AB,AC所在的直线方程。
类型二 三角形中有关直线方程的求解
变式拓展
若△ABC在第一象限,A(1,1),B(5,1),且点C在直线
AB的上方,∠CAB=45o,∠B=60o,则直线AC的方程
是___________ ,直线BC的方程是___________
数学应用
例4、求证:无论m取何值,直线y-2=m(x+3)总过一个定
点,并求出该定点坐标。
类型三 直线过定点问题的研究
数学练习
已知直线kx-y+1-2k =0,当k变化时直线恒过一个定点
________
课堂检测
1、写出下列直线的点斜式方程
(1)经过点A(3,-1),斜率是 ;
(2)经过点B ,倾斜角是30o;
(3)经过点C(0,3),倾斜角是0o;
(4)经过点D(4,-2),倾斜角是120o。
2、填空题
(1)已知直线的点斜式方程是y-2=x-1,那么直线的斜
率为___________,倾斜角为_____________
(2)已知直线的点斜式方程是 , 那么直线
的斜率为___________,倾斜角为_____________
课堂小结
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
2、直线斜率的两个定义
3、直线倾斜角和斜率的取值范围
1、直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
注意:(1)直线向上方向; (2)x轴的正方向。
复习回顾
4、直线倾斜角和斜率的关系
复习回顾
情境导入
飞逝的流星形成了一条美丽的弧线,这条弧线可以看做是满足某种运动规律的点的集合;在平面直角坐标系中,直线也可以看做是满足某种条件的点的集合,直线的位置既可由两点唯一确定,也可由一点和一个方向来确定。
数学探究
数学探究
数学建构
1、直线的点斜式方程
数学探究
数学探究
数学应用
类型一 利用点斜式、斜截式求直线方程
例1、求下列直线的点斜式方程
(1)直线经过点P(-2,3),斜率为2;
(2)直线经过点A (-1,2),且倾斜角α=135o;
(3)直线的斜率为2,经过点(0,1)。
变式拓展
已知直线的斜率为k,与y轴的交点是P(0,b),求这条直线的方程。
数学建构
2、直线的斜截式方程
数学探究
数学探究
问题8:斜截式与点斜式存在什么关系?
斜截式是点斜式的特殊情况,有时比点斜式更方便
问题9:斜截式y=kx+b在形式上与一次函数的表达式一样,
它们之间有什么差别?
只有当k≠0时,斜截式方程才是一次函数的表达式
数学练习
1、直线3x+2y-6=0的斜率为______ ,纵截距为_______
2、若直线的斜率是 ,在y 轴上的截距是-2,则直线的
方程为___________,若直线的倾斜角为135o,在y轴
上的截距为0,则直线的方程为___________
数学应用
例2、若直线l经过点A(-1,-3),其倾斜角等于直线
的倾斜角的2倍,求直线 l的方程。
数学应用
例3、已知△ABC的顶点为A(-1,2),B(-3,2),又AC的斜
率为 ,求直线AB,AC所在的直线方程。
类型二 三角形中有关直线方程的求解
变式拓展
若△ABC在第一象限,A(1,1),B(5,1),且点C在直线
AB的上方,∠CAB=45o,∠B=60o,则直线AC的方程
是___________ ,直线BC的方程是___________
数学应用
例4、求证:无论m取何值,直线y-2=m(x+3)总过一个定
点,并求出该定点坐标。
类型三 直线过定点问题的研究
数学练习
已知直线kx-y+1-2k =0,当k变化时直线恒过一个定点
________
课堂检测
1、写出下列直线的点斜式方程
(1)经过点A(3,-1),斜率是 ;
(2)经过点B ,倾斜角是30o;
(3)经过点C(0,3),倾斜角是0o;
(4)经过点D(4,-2),倾斜角是120o。
2、填空题
(1)已知直线的点斜式方程是y-2=x-1,那么直线的斜
率为___________,倾斜角为_____________
(2)已知直线的点斜式方程是 , 那么直线
的斜率为___________,倾斜角为_____________
课堂小结
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
