北师大版九年级下下册第三章圆中考压轴题(Word版,附答案解析)
文档属性
| 名称 | 北师大版九年级下下册第三章圆中考压轴题(Word版,附答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览


文档简介
圆中考压轴题
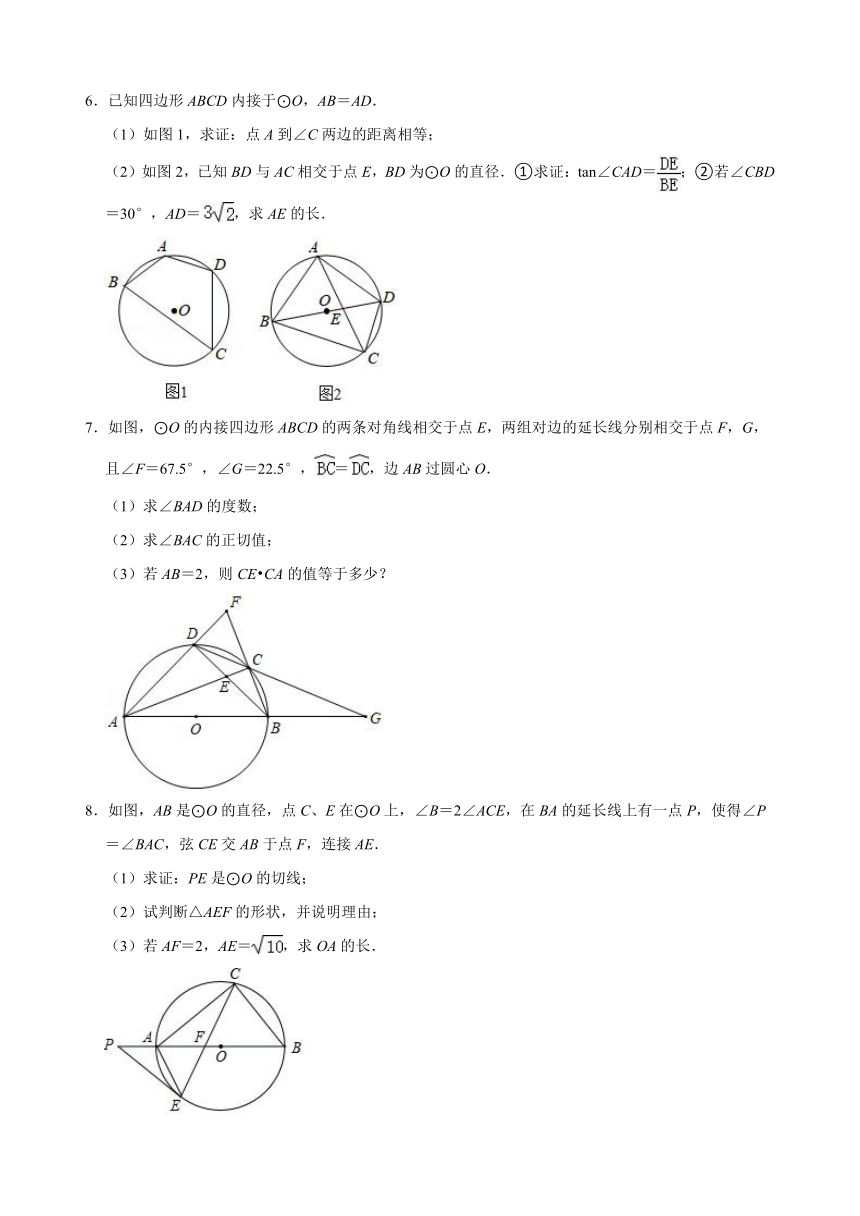
1.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式;
②如图②,连接OE,OD,若=,求y的值.
2.已知AB、CD为⊙O的两条弦,AB∥CD.
(1)如图1,求证弧AC=弧BD;
(2)如图2,连接AC、BC、OA、BD,弦BC与半径OA交于点G,延长AO交CD于点E,连接BE,使BE=BD,若OA⊥BC,求证:四边形ABEC为菱形;
(3)在(2)的条件下,CH与⊙O相切于点C,连接CO并延长交BE于点F,延长BE交CH于点H,OF=11,sin∠BDC=,求CH长.
3.如图,以Rt△BCE的直角边BC为直径作⊙O,交斜边EC于点A,AD⊥BC于点D,点F是BE的中点,连接CF与AD相交于点G,延长AF与CB的延长线相交于点P.
(1)求证:PA是⊙O的切线;
(2)求证:点G为AD的中点;
(3)若2FG=EB,且⊙O的半径长为3,求BD的长度.
4.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC;
②若CM=10,tan∠CMO=2,求ON的长.
5.如图,AB是⊙O的直径,C、D是⊙O上两点.AE与过点C的切线垂直,垂足为E,直线EC与直径AB的延长线相交于点P,弦CD交AB于点F,连接AC、AD、BC、BD.
(1)若∠ABC=∠ABD=60°,判断△ACD的形状,并证明你的结论;
(2)若CD平分∠ACB,求证:PC=PF;
(3)在(2)的条件下,若AD=5,PF=5,求由线段PC、和线段BP所围成的图形(阴影部分)的面积.
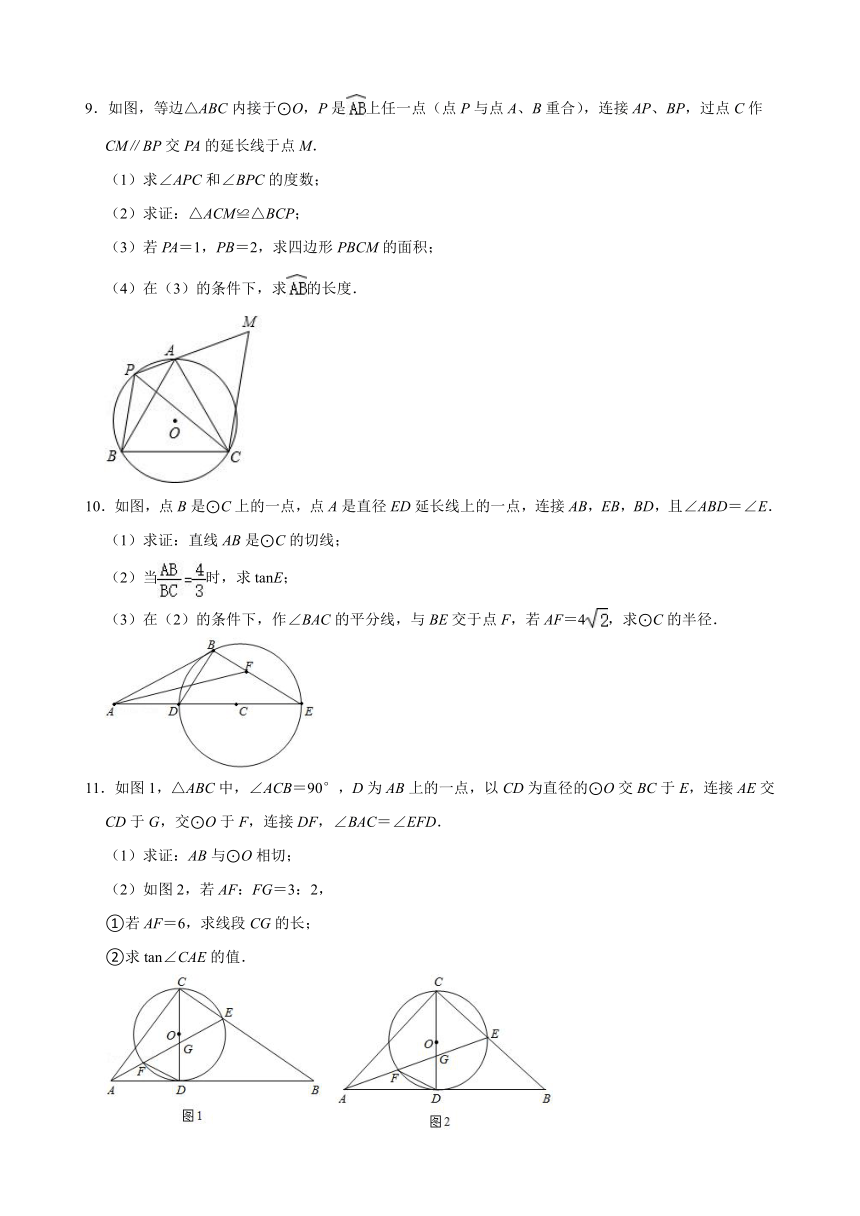
6.已知四边形ABCD内接于⊙O,AB=AD.
(1)如图1,求证:点A到∠C两边的距离相等;
(2)如图2,已知BD与AC相交于点E,BD为⊙O的直径.①求证:tan∠CAD=;②若∠CBD=30°,AD=,求AE的长.
7.如图,⊙O的内接四边形ABCD的两条对角线相交于点E,两组对边的延长线分别相交于点F,G,且∠F=67.5°,∠G=22.5°,=,边AB过圆心O.
(1)求∠BAD的度数;
(2)求∠BAC的正切值;
(3)若AB=2,则CE CA的值等于多少?
8.如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
(1)求证:PE是⊙O的切线;
(2)试判断△AEF的形状,并说明理由;
(3)若AF=2,AE=,求OA的长.
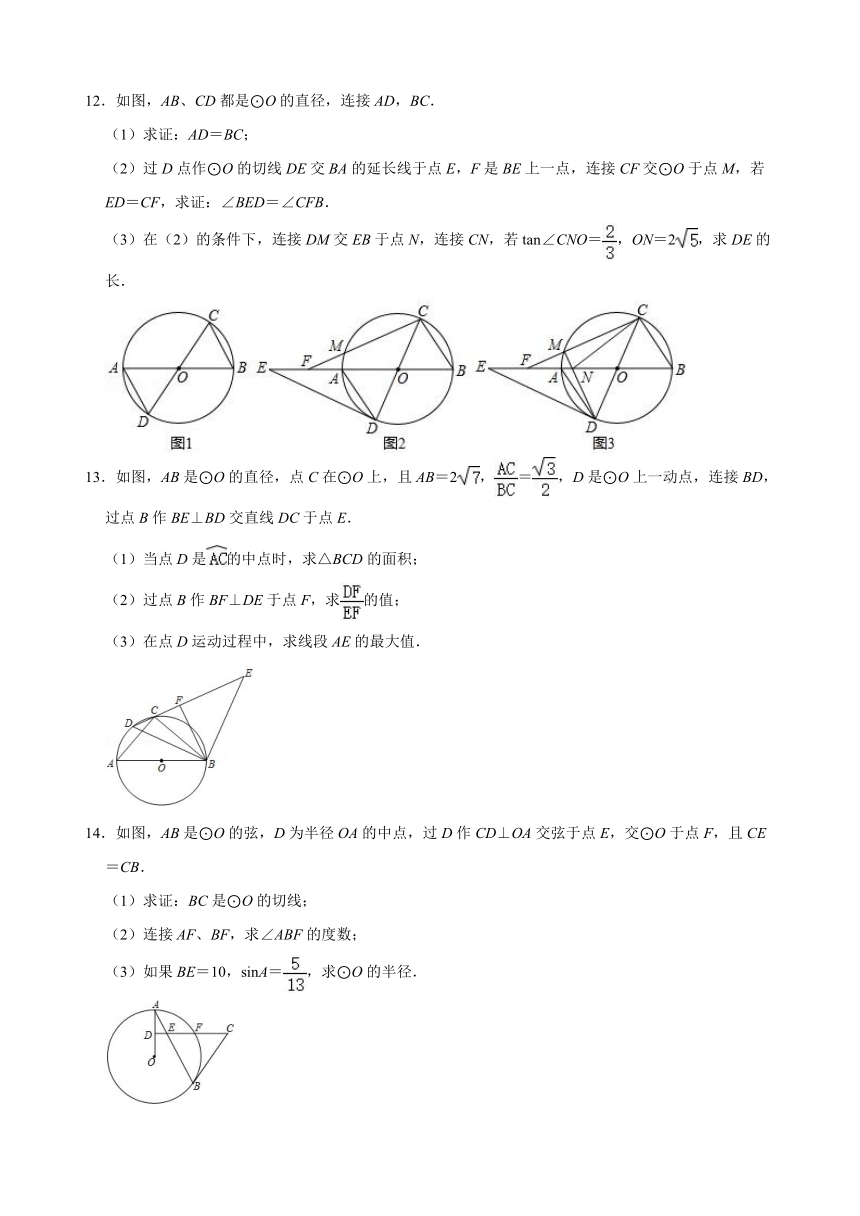
9.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积;
(4)在(3)的条件下,求的长度.
10.如图,点B是⊙C上的一点,点A是直径ED延长线上的一点,连接AB,EB,BD,且∠ABD=∠E.
(1)求证:直线AB是⊙C的切线;
(2)当时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=4,求⊙C的半径.
11.如图1,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交BC于E,连接AE交CD于G,交⊙O于F,连接DF,∠BAC=∠EFD.
(1)求证:AB与⊙O相切;
(2)如图2,若AF:FG=3:2,
①若AF=6,求线段CG的长;
②求tan∠CAE的值.
12.如图,AB、CD都是⊙O的直径,连接AD,BC.
(1)求证:AD=BC;
(2)过D点作⊙O的切线DE交BA的延长线于点E,F是BE上一点,连接CF交⊙O于点M,若ED=CF,求证:∠BED=∠CFB.
(3)在(2)的条件下,连接DM交EB于点N,连接CN,若tan∠CNO=,ON=2,求DE的长.
13.如图,AB是⊙O的直径,点C在⊙O上,且AB=2,=,D是⊙O上一动点,连接BD,过点B作BE⊥BD交直线DC于点E.
(1)当点D是的中点时,求△BCD的面积;
(2)过点B作BF⊥DE于点F,求的值;
(3)在点D运动过程中,求线段AE的最大值.
14.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=,求⊙O的半径.
15.如图,在Rt△ABC中,∠C=90°,O为AB上一点,以点O为圆心,OA为半径作⊙O,分别交AB、AC于点E、F,且与BC相切于点D,连接OF.解答下列问题:
(1)∠BAC与∠OFA之间的关系是 ;
(2)求证:∠AFO=2∠BAD;
(3)若=,求tan的值.
16.如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=3,EF=5,
①求证:DE=EF;
②求⊙O的半径.
17.如图,⊙O是△ABC的外接圆,AB是的直径,D是AB延长线上的一点,连接DC,∠DCB=∠A,CE⊥AB于点E.
(1)求证DC是⊙O的切线;
(2)若AC=4,tan∠BCE=,求DC的长;
(3)在(2)的条件下,若M是线段AC上一动点,求OM+AM的最小值.
18.如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若tan∠ADC=,AC=2,求⊙O的半径;
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
19.如图1,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.
(1)求证:△ADG∽△CFG.
(2)若G是的中点,当CG与△ADE的一边平行时,求的值.
(3)如图2,点E是OB的中点,AB=8,连接BG,BD,BC.当DG+CG=6时,求cosF的值.
20.如图,四边形BCDE是⊙O的内接四边形,DE是⊙O的直径,BC、ED的延长线交于点A,连接CE、BD交于点F,DF2=FC FE,点H是线段CE上一点连接BH、DH.
(1)求证:DF=BF;
(2)若∠BEC=∠DBH,∠BDE=45°,求;
(3)在(2)的条件下,若AE=AC,CB+DE=2+2.求线段AC的长度.
21.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,连接OA、OB、OC,延长BO与AC交于点D,与⊙O交于点F,延长BA到点G,使得∠BGF=∠GBC,连接FG.
(1)求证:FG是⊙O的切线;
(2)若⊙O的半径为3.
①当OD=2,求AD的长度; ②当△OCD是直角三角形时,求△ABC的面积.
22.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切:
(2)若,求的值;
(3)在(2)的条件下,若⊙O的半径为4,PD=OD,求EC的长.
23.如图,在△ABC中,∠A=90°,D是边AC上一动点,且不与A,C两点重合,连接BD,过点D作DE⊥BD交边BC于点E,△BDE的外接圆交边AB于另一点F,连接DF.
(1)求证:△ADF∽△DBE.
(2)当AB=6,AC=8时.
①若AD=3AF,求AD的长.
②当线段DE,DF,BF中有两条相等时,求出所有符合条件的tan∠ADF的值.
(3)若BD平分∠ABC,S△ADF=1,S△BDE=6,则S△CDE= .
24.如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
25.如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为,△ABC的面积为2,求CD的长;
(3)在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若=,求BF的长.
26.如图1,以△ABC的边AC为直径作⊙O交BC于点D,连接AD,点E为AD上一点(不与端点重合),连接CE,作DF⊥CE于点F,延长DF交AC于点M,交BA的延长线于点G,∠BGD=∠ACE.
(1)求证:BG是⊙O的切线;
(2)求证:;
(3)如图2,延长CE交AB于点H,若HE=4,∠ACH=∠BCH,sin∠BGD=,求BC的长.
27.如图,点I是O△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)求证:DG是⊙O的切线;
(2)若DE=4,BE=5,求DI的长;
(3)若sin∠ACD=,CD=10,求△ACD的内心到点O的距离.
28.如图,以Rt△ABC的斜边AC为直径作⊙O,点D在半径OC上,过点D作AC的垂线,分别交弦BC于点E,交⊙O于F.在射线DE上取点G,连接GB并延长交CA的延长线于点H,且满足GB=GE.
(1)求证:HG是⊙O的切线;
(2)若GE=BE,HB=.
(i)求⊙O的半径;
(ii)如图2,连接AF,交弦BC于点M,若AF∥HG,求线段OD的长.
29.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E,连接AD,CD.
(1)求证:DE与⊙O相切;
(2)若AB=6,tanA=,求BE的长;
(3)线段AB,BE,CE之间有何数量关系?写出你的结论并证明.
30.如图,AB是⊙O的直径,AC是弦,点E在圆外,OE⊥AC于点D,BE交⊙O于点F,连接BD、BC、CF,∠BFC=∠AED.
(1)求证:AE是⊙O的切线;
(2)求证:OB2=OD OE;
(3)设△BAD的面积为S1,△BDE的面积为S2,若tan∠ODB=,求的值.
31.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)求证:AF为⊙O的切线;
(2)当点D为EF的中点时,求证:AD2=AO AE;
(3)在(2)的条件下,若sin∠BAC=,AF=2,求BF的长.
32.如图1,O是△ABC的边BC的中点,⊙O与BC交于E、F两点,与AB相切于点D,连接AO交⊙O于点P,=.
(1)猜想AC与⊙O的位置关系,并证明你的猜想.
(2)如图2,延长AO交⊙O于Q点,连接DE、DF,DQ,FQ,FQ=,ED=5,求DQ的长.
(3)如图3,若DE=5,连接DF、DP、PF,设DP=x,△DPF的面积为y,求y与x之间的函数关系式.
33.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD∥AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:AF是⊙O的切线;
(2)求证:AB2﹣BE2=BE EC;
(3)如图2,若点G是△ACD的内心,BC BE=64,求BG的长.
答案与解析
1.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式;
②如图②,连接OE,OD,若=,求y的值.
【解答】(1)证明:∵∠ACB=90°,且⊙O经过B、C、E,
∴直线BE为⊙O的直径,
∴∠BDE=90°,
∴∠CBD+∠CED=180°,
∵∠AED+∠CED=180°,
∴∠AED=∠CBD,
∵CA=CB,
∴∠CAD=∠CBA,
∴∠DEA=∠DAE,
∴AD=ED.
(2)解:∵∠EDA=∠ACB=90°,∠DAE=∠CBA=45°,
∴△ADE∽△CAB,
∴AE=4,AD=DE,
∴AD=DE==2,CA=AE+CE=2+4=6,且,
即,
∴AB=6,
∴DB=AB﹣AD=4,
∴BE===2,
∴⊙O的半径为.
(3)①∵tan∠DCB=y,
∴,,
∴sin∠DCB= sin∠CBD=,cos∠BCD=,
∴tan∠DCB===y,
设EC=m,
∴AE=mx,
∴BC=m+mx=m(1+x),BD=BC﹣AD,AD=AE,
∴BD=m(1+x)﹣mx=m(1+),
∴∠CED=45°,
∴cos∠CED=﹣=,
∴CD2=m2+m2x2+m2x,
∴y===,
②设CE=n,AE=nx,
∴DE=,AC=n(1+x)=BC,
∴S△ABC=AC BC=n2(1+x)2,BE===n,
∴OE=BE=且△OED为等腰三角形,
∴O点到DE的距离为:==n,
∴S△OED=×nx n=n2,
∵=,
∴=,
∵x>0,
∴x=3,
∴y==.
2.已知AB、CD为⊙O的两条弦,AB∥CD.
(1)如图1,求证弧AC=弧BD;
(2)如图2,连接AC、BC、OA、BD,弦BC与半径OA交于点G,延长AO交CD于点E,连接BE,使BE=BD,若OA⊥BC,求证:四边形ABEC为菱形;
(3)在(2)的条件下,CH与⊙O相切于点C,连接CO并延长交BE于点F,延长BE交CH于点H,OF=11,sin∠BDC=,求CH长.
【解答】(1)证明:连接BC,
∵AB∥CD,
∴∠ABC=∠BCD,
∴=;
(2)证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵四边形ABDC是圆的内接四边形,
∴∠BAC+∠BDC=180°,
∴∠ACD=∠BDC,
∵=,
∴AC=BD,
∵BE=BD,
∴AC=BE,∠BED=∠BDC,
∴∠BED=∠ACD,
∴AC∥BE,
∴四边形ABEC是平行四边形,
∵OA⊥BC,
∴平行四边形ABEC是菱形;
(3)解:如图3,延长CF交⊙O于点N,连接BN,
∵CN是直径,
∴∠CBN=90°,
∵AE⊥BC,
∴AE∥BN,
∴∠AOC=∠BNC,
∵∠BDC=∠BNC,
∴∠AOC=∠BDC,
∵sin∠BDC=,
∴sin∠AOC==,
设CO=25x,CG=24x,
∴GO===7x,
∵∠ACD=∠BDC,
∴∠ACD=∠AOC,
又∵∠CAE=∠CAO,
∴△ACO∽△AEC,
∴∠AEC=∠OCA,
∵四边形ABEC是菱形,
∴AC=CE,AE⊥BC,AG=GE,
∴∠CAE=∠CEA,
∴∠CAE=∠ACO,
∴AO=CO=25x,
∴AG=18x=GE,
∴OE=11x,
∵AC∥EB,
∴,
∴=,
∴x=1,
∴CO=25,AG=18,CG=24,
∴CF=36,
∵AC∥BE,
∴∠ACF=∠CFE,
∴∠CFE=∠CAO,
∵CH与⊙O相切于点C,
∴CH⊥CF,
∴∠FCH=90°=∠AGC,
∴△AGC∽△FCH,
∴,
∴=,
∴CH=48.
3.如图,以Rt△BCE的直角边BC为直径作⊙O,交斜边EC于点A,AD⊥BC于点D,点F是BE的中点,连接CF与AD相交于点G,延长AF与CB的延长线相交于点P.
(1)求证:PA是⊙O的切线;
(2)求证:点G为AD的中点;
(3)若2FG=EB,且⊙O的半径长为3,求BD的长度.
【解答】解:(1)证明:如图,连接AO,AB,
∵BC是⊙O的直径,
∴∠BAC=90°,
在Rt△BAE中,F是斜边BE的中点,
∴AF=FB=EF,
∴∠FBA=∠FAB,
又∵OA=OB,
∴∠ABO=∠BAO,
∵∠EBO=90°,
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA是⊙O的切线;
(2)证明:∵BC是⊙O的直径,∠EBO=90°,,
∴EB⊥BC.BE是⊙O的切线
又∵AD⊥BC,
∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC,
∴,,
∴,
∵F是斜边BE的中点,
∴BF=EF,
∴DG=AG,
∴点G为AD的中点;
(3)解:过点F作FH⊥AD于点H,如图,
∵BD⊥AD,FH⊥AD,
∴FH∥BC.
由(2)知,∠FBA=∠BAF,
∴BF=AF.
由已知,有2FG=EB,点F是BE的中点,
∴BF=FG,
∴AF=FG,即△AFG是等腰三角形.
∵FH⊥AD,
∴AH=GH,
∵DG=AG,
∴DG=2HG,
即,
∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,BD=FH,
∵FH∥BC,
∴△HFG∽△DCG,
∴,
∵⊙O的半径长为3,
∴BC=6.
∴,
解得BD=2.
∴BD=2.
4.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC;
②若CM=10,tan∠CMO=2,求ON的长.
【解答】证明:(1)连接OD,如图1,
∵PD为⊙O切线,
∴∠ODP=90°,
∵AB⊥CD,且AB为⊙O直径,
∴AB垂直平分CD,
∴PC=PD,
∴∠PCD=∠PDC,
又∵OC=OD,
∴∠OCD=∠ODC,
∴∠OCP=∠OCD+∠PCD=∠ODC+∠PDC=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)①∵AB⊥CD,
∴∠CEP=90°,
∴∠ECP+∠MPO=90°,
又∠OCD+∠ECP=90°,
∴∠MPO=∠OCD,
又OM平分∠COP,
∴∠CON=∠MOP,
∴△OMP∽△ONC;
(2)②∵∠CNM=∠CON+∠OCN,
∠CMO=∠CPO+∠MOP,
∴∠CNM=∠CMN,
∴CM=CN=10,
过点C作CG⊥MN于G,
∵tan∠CMO=2,
∴NG=MG=2,CG=4,
在Rt△OCM中,由勾股定理得:OM=,
∴ON=OM﹣MN=10.
5.如图,AB是⊙O的直径,C、D是⊙O上两点.AE与过点C的切线垂直,垂足为E,直线EC与直径AB的延长线相交于点P,弦CD交AB于点F,连接AC、AD、BC、BD.
(1)若∠ABC=∠ABD=60°,判断△ACD的形状,并证明你的结论;
(2)若CD平分∠ACB,求证:PC=PF;
(3)在(2)的条件下,若AD=5,PF=5,求由线段PC、和线段BP所围成的图形(阴影部分)的面积.
【解答】解:(1)△ACD是等边三角形,
理由如下:
=,
∴∠ACD=∠ABD=60°,
∵=,
∴∠ADC=∠ABC=60°,
∴△ACD是等边三角形;
(2)如图1,
连接OC,OD,
∵PC切⊙O于C,
∴OC⊥PC,
∴∠PCO=90°,
∴∠OCF+∠PCF=90°,
∵CD平分∠ACB,
∴=,
∴∠DOB=∠AOD=90°,
∴∠ODF+∠OFD=90°,
∵OC=OD,
∴∠ODF=∠OCF,
∴∠PCF=∠OFD,
又∵∠CFP=∠OFD,
∴∠PFC=∠CFP,
∴PC=PF;
(3)由(2)知,
=,
∴AD=BD=5,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AB==10,
∴OC=5,
∵PC=PF,
∴PC=5,
∵tan∠BOC==
∴∠BOC=60°,
∵S△PCO=OC PC==,
S扇形BOC==,
∴S阴影=S△PCO﹣S扇形BOC=﹣.
6.已知四边形ABCD内接于⊙O,AB=AD.
(1)如图1,求证:点A到∠C两边的距离相等;
(2)如图2,已知BD与AC相交于点E,BD为⊙O的直径.①求证:tan∠CAD=;②若∠CBD=30°,AD=,求AE的长.
【解答】证明:(1)如图1,连接AC,
∵AB=AD,
∴,
∴∠ACB=∠ACD,
∴点A到∠C两边的距离相等;
(2)①∵,
∴∠CAD=∠CBD,
∵BD为直径,
∴∠BCD=90°,
∴tan∠CAD=tan∠CBD=,
如图2,过点D作DQ∥EC,交BC延长线于点Q,
∴∠ACB=∠Q,∠ACD=∠CDQ,
又由(1)知:∠ACB=∠ACD,
∴∠CDQ=∠Q,
∴CD=CQ,
∵CE∥DQ,
∴
∴,
∴tan∠CAD=,
②如图,
由(2)①得:∠CAD=∠CBD=30°,
则tan∠CAD==,
设DE=a,则BE=a,
∵BD为直径,
∴∠BAD=90°,
∵AB=AD=3,
∴BD=6,
∴a+a=6,
解得:a=3,
∴DE=3﹣3,BE=9﹣3,
又∵∠BCD=90°,
∴CD=BD sin∠CBD=3,
∵∠BDC=∠BAC,∠ABD=∠ACD,
∴△BAE∽△CDE,
∴,
∴AE=(3﹣3)×=3﹣3.
7.如图,⊙O的内接四边形ABCD的两条对角线相交于点E,两组对边的延长线分别相交于点F,G,且∠F=67.5°,∠G=22.5°,=,边AB过圆心O.
(1)求∠BAD的度数;
(2)求∠BAC的正切值;
(3)若AB=2,则CE CA的值等于多少?
【解答】解:(1)如图,∵AB经过圆心O,
∴AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵∠F=67.5°,
∴∠DAC=∠ACB﹣∠F=90°﹣67.5°=22.5°,
∵,
∴∠DAC=∠BAC=22.5°,
∴∠BAD=22.5°+22.5°=45°.
(2)如图,设⊙O的半径为r,连接OD,则OD=OA=OB=r,
∴∠ODA=∠OAD=45°,
∴∠AOD=∠GOD=90°,
∵∠BDC=∠BAC=22.5°,∠G=22.5°,
∴∠BDC=∠BAC=∠BGC,
∴BG=BD==r,
∴tan∠BAC=tan∠BGC===.
(3)如图,∵∠ACB=90°,tan∠BAC=,
∴=tan∠BAC=,
∴AC=()BC,
由AC2+BC2=AB2,且AB=2,得()2BC2+BC2=22,
解得,BC2=;
∵,
∴∠CBE=∠CAB,
∵∠BCE=∠ACB,
∴△BCE∽△ACB,
∴,
∴CE CA=BC2=.
8.如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
(1)求证:PE是⊙O的切线;
(2)试判断△AEF的形状,并说明理由;
(3)若AF=2,AE=,求OA的长.
【解答】(1)证明:连接OE,
∴∠AOE=2∠ACE,
∵∠B=2∠ACE,
∴∠AOE=∠B,
∵∠P=∠BAC,
∴∠ACB=∠OEP,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OEP=90°,
∴PE是⊙O的切线;
(2)解:△AEF是等腰三角形,理由如下:
∵OA=OE,
∴∠OAE=∠OEA.
∵∠AFE=∠AOE+∠EFO,∠AOE=∠B,∠B=∠AEF,
∴∠AOE=∠AEF.
∴∠AFE=∠AEF+∠FEO=∠OEA.
∴∠OAE=∠AFE.
∴△AEF是等腰三角形;
(3)∵OA=OE,
∴∠OAE=∠OEA,
∵AE=EF,
∴∠EAF=∠AFE,
∴∠OAE=∠OEA=∠EAF=∠AFE,
∴△AEF∽△AOE,
∴=,
∵AF=2,AE=EF=,
∴OA=5.
9.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积;
(4)在(3)的条件下,求的长度.
【解答】解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵,,
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°﹣∠BPM=180°﹣(∠APC+∠BPC)=180°﹣120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PCB=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
在△ACM和△BCP中,
,
∴△ACM≌△BCP(AAS);
(3)∵CM∥BP,
∴四边形PBCM为梯形,
作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP,AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+AMB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=,
∴S四边形PBCM=(PB+CM)×PH=(2+3)×=;
(4)过点B作BQ⊥AP,交AP的延长线于点Q,过点A作AN⊥BC于点N,连接OB,
∵∠APC=∠BPC=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴PQ=PB=1,
在Rt△BPQ中,BQ=,
在Rt△AQB中,AB=,
∵△ABC为等边三角形,
∴AN经过圆心O,
∴BN=AB=,
∴AN=,
在Rt△BON中,设BO=x,则ON=,
∴,
解得:x=,
∵∠BOA=∠BCA=120°,
∴的长度为.
10.如图,点B是⊙C上的一点,点A是直径ED延长线上的一点,连接AB,EB,BD,且∠ABD=∠E.
(1)求证:直线AB是⊙C的切线;
(2)当时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=4,求⊙C的半径.
【解答】证明:(1)连接CB,如图,
∵ED为圆的直径,
∴∠DBE=90°.
∴∠CBD+∠CBE=90°.
∵CB=CE,
∴∠CBE=∠CEB,
∴∠CBD+∠CEB=90°.
∵∠ABD=∠E,
∴∠CBD+∠ABD=90°,
即∠ABC=90°,
∴AB⊥BC.
∴直线AB是⊙C的切线;
(2)过点D作DH⊥AB于点H,如图,
则DH∥BC.
∵,
∴设AB=4x,则BC=3x.
∵AB⊥BC,
∴AC==5x,
∵CD=CB=3x,
∴AD=AC﹣CD=2x.
∵DH∥BC,
∴=.
∴,.
∴DH=x,AH=x.
∴BH=AB﹣AH=x,
在Rt△BHD中,tan∠HBD=.
∵∠ABD=∠E,
∴tanE=tan∠HBD=.
(3)过点F作FM⊥CE于M,如图,
∵tanE=,
∴.
由(2)知:AB=4x,BC=3x,AC=5x,AD=2x,
∵CE=CB=3x,
∴AE=AD+CD+CE=8x.
∵AF是∠BAC的平分线,
∴.
∴FE=BE.
在Rt△BDE中,tanE==,
则BE=2BD.
∵BD2+BE2=DE2,
∴BD2+(2BD)2=(6x)2.
∴BD=,
∴BE=2BD=x.
∴FE=x.
在Rt△BDE中,tanE==,则ME=2MF.
∵FM2+ME2=FE2,
∴.
∴FM=x.
∴ME=2FM=x,
∴AM=AE﹣ME=(8﹣)x=x.
在Rt△AFM中,
∵AM2+FM2=AF2,
∴.
解得:x=±(负数不合题意,舍去).
∴x=.
∴⊙C的半径CE=3x=.
11.如图1,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交BC于E,连接AE交CD于G,交⊙O于F,连接DF,∠BAC=∠EFD.
(1)求证:AB与⊙O相切;
(2)如图2,若AF:FG=3:2,
①若AF=6,求线段CG的长;
②求tan∠CAE的值.
【解答】证明:(1)∵∠BCD=∠DFE,∠BAC=∠EFD,
∴∠BCD=∠BAC.
∵∠ACB=90°,
∴∠BAC+∠B=90°,
∴∠BCD+∠B=90°.
即∠CDB=90°,
∴CD⊥AB.
∴AB与⊙O相切;
解:(2)①连接CF,如图,
∵AF:FG=3:2,AF=6,
∴FG=4.
∴AG=AF+FG=10.
∵CD为⊙O的直径,
∴∠CFD=90°,
∴∠FCD+∠FDC=90°.
∵∠CEF=∠FDC,
∴∠FCD+∠FEC=90°.
∵∠ACB=90°,
∴∠CAE+∠CEF=90°.
∴∠FCD=∠CAE.
∵∠CGF=∠AGC,
∴△CGF∽△AGC.
∴.
∴CG2=AG GF=4×10=40.
∴CG=2.
②过点F作FH⊥CD于点H,如图,
∵FH⊥CD,AD⊥CD,
∴FH∥AD.
∴.
设DH=3x,则GH=2x,
∴CH=HG+CG=2+2x.
∵∠CFD=90°,FH⊥CD,
∴△FHD∽CHF.
∴.
∴FH2=HD CH=3x(2+2x).
在Rt△FGH中,
∵FH2+CH2=FG2,
∴3x(2+2x)+(2x)2=42.
解得:x=或x=﹣(不合题意,舍去).
∴GH=,FH=,
∴CH=CG+GH=.
在Rt△FCH中,tan∠FCH=.
∵∠FCH=∠CAE,
∴tan∠CAE=tan∠FCH=.
12.如图,AB、CD都是⊙O的直径,连接AD,BC.
(1)求证:AD=BC;
(2)过D点作⊙O的切线DE交BA的延长线于点E,F是BE上一点,连接CF交⊙O于点M,若ED=CF,求证:∠BED=∠CFB.
(3)在(2)的条件下,连接DM交EB于点N,连接CN,若tan∠CNO=,ON=2,求DE的长.
【解答】(1)证明:∵在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴AD=BC;
(2)证明:如图2,过点C作CG⊥AB于G,过点D作DH⊥AB于H,
在△ODH和△OCG中,
,
∴△ODH≌△OCG(AAS),
∴DH=CG,
在Rt△EDH和Rt△FCG中,
,
∴Rt△EDH≌Rt△FCG(HL),
∴∠BED=∠CFB;
(3)解:如图3,过点C作CG⊥AB于G,过点D作DH⊥AB于H,
∵CD是⊙O的直径,
∴∠CMD=90°,
∴∠FMN=90°,
∴∠MFN+∠FNM=90°,
∵ED是⊙O的切线,
∴∠ODE=90°,
∴∠NOD+∠E=90°,
∵∠BED=∠CFB,∠FNM=∠DNO,
∴∠DNO=∠NOD,
∴DN=DO,
∵DH⊥AB,ON=2,
∴NH=HO=,
由(2)可知:△ODH≌△OCG,
∴OG=OH=,
∴NG=3,
∵tan∠CNO==,
∴CG=2,
由勾股定理得:OC===5,
∵∠EDO=∠CGO=90°,∠EOD=∠COG,
∴△EOD∽△COG,
∴=,即=,
解得:ED=10.
13.如图,AB是⊙O的直径,点C在⊙O上,且AB=2,=,D是⊙O上一动点,连接BD,过点B作BE⊥BD交直线DC于点E.
(1)当点D是的中点时,求△BCD的面积;
(2)过点B作BF⊥DE于点F,求的值;
(3)在点D运动过程中,求线段AE的最大值.
【解答】解:(1)过点D作DH⊥BC交BC的延长线于点H,连接OD交AC于点M,
∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AC,
设AC=x,则BC=2x,
在Rt△ACB中,AC2+BC2=AB2,
∴(x)2+(2x)2=(2)2,
解得x=2或﹣2(舍去),
∴AC=2,BC=4,
∵点D是的中点,
∴OD⊥AC,AM=CM,
∴四边形CHDM是矩形,
∴DH=CM=AC=,
∴S△BCD=×DH×BC=××4=2;
(2)在Rt△ACB中,cos∠CAB===,
∵∠EDB=∠CAB,
∴cos∠EDB=∠cosCAB=,
在Rt△BFD中,cos∠FDB=,
∴DF=BD,
在Rt△BED中,cos∠EDB=,
∴BD=DE,
∴DF=DE,
∴=;
(3)当点D与点A重合时,AE的值最大,此时BD与AB重合,
由(2)知,BD=DE,且BD=AB=2,
∴AE=DE=.
14.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=,求⊙O的半径.
【解答】(1)证明:连接OB,
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC,
又∵CD⊥OA,
∴∠A+∠AED=∠A+∠CEB=90°,
∴∠OBA+∠ABC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:如图1,连接OF,AF,BF,
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°,
∴∠ABF=∠AOF=30°;
(3)解:连接OF,如图2所示:
∵DA=DO,CD⊥OA,
∴AF=OF=OA,
过点O作OG⊥AB于点G,则AG=BG,
在Rt△AOG中,sin∠BAO===,
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,
∴AB=10+13x,
则AG=AB=5+x,
又∵Rt△AOG中,sin∠BAO=,则=,
则=,
解得x=,
∴AO=24x=.
15.如图,在Rt△ABC中,∠C=90°,O为AB上一点,以点O为圆心,OA为半径作⊙O,分别交AB、AC于点E、F,且与BC相切于点D,连接OF.解答下列问题:
(1)∠BAC与∠OFA之间的关系是 相等 ;
(2)求证:∠AFO=2∠BAD;
(3)若=,求tan的值.
【解答】解:(1)∵OA=OF,
∴∠OAF=∠OFA,
即∠BAC=∠OFA,
故答案为:相等;
(2)证明:连接OD,如图,
∵BC为切线,
∴OD⊥BC,
∵∠C=90°,
∴OD∥AC,
∴∠ODA=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,
∴∠OAC=2∠OAD,
∵OA=OF,
∴∠OAC=∠AFO,
∴∠AFO=2∠BAD;
(3)作OH⊥AF于H,如图,则AH=HF,
∵=,
∴设AH=HF=2x,则CF=3x,
∵∠ODC=∠C=∠OHC=90°,
∴四边形ODCH为矩形,
∴OH=CD,OD=CH=2x+3x=5x,
在Rt△AOH中,OH==x,
∴CD=x,
在Rt△ACD中,tan∠CAD===.
∴tan的值为.
16.如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=3,EF=5,
①求证:DE=EF;
②求⊙O的半径.
【解答】(1)证明:如图(1),连接BD,
∵∠BAD=90°,
∴BD是⊙O的直径,
∴∠BCD=∠DCE=90°,
∴∠DEC+∠CDE=90°,
∵∠BAC=∠BDC,∠BAC=∠DEC,
∴∠BDC+∠CDE=90°,即∠BDE=90°,
∴DE是⊙O的切线.
(2)①证明:由(1)得:∠BDE=90°,
∴∠ADB+∠EDF=90°,
∵∠BAD=90°,
∴∠ABC+∠F=90°,
∴∠ADB+∠EDF=∠ABC+∠F,
∵AB=AC,
∴∠ADB=∠ABC,
∴∠EDF=∠F,
∴DE=EF.
②解:∵DE=EF,
∴DE=EF=5,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴CD===4,
∠BDC+∠DBC=90°,
又∵∠BDC+∠EDC=90°,
∴∠DBC=∠EDC,
∴△CDE∽△CBD,
∴,
∴,
∴BD=,
∴⊙O的半径为.
17.如图,⊙O是△ABC的外接圆,AB是的直径,D是AB延长线上的一点,连接DC,∠DCB=∠A,CE⊥AB于点E.
(1)求证DC是⊙O的切线;
(2)若AC=4,tan∠BCE=,求DC的长;
(3)在(2)的条件下,若M是线段AC上一动点,求OM+AM的最小值.
【解答】(1)证明:如图,
根据题意连接OC,则有OC=OA,
∴∠A=∠OCA=∠BCD,
∵AB是圆的直径,
∴∠ACB=90°,即∠OCA+∠OCB=90°,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴OC⊥CD,
∴DC是⊙O的切线.
(2)由(1)可知∠A+∠ABC=90°,∠ECB+∠ABC=90°,
∴∠A=∠ECB,
∴Rt△ABC~Rt△CBE,
∴=,
∵AC=4,tan∠BCE=,
∴==,解得BC=2,
∴AB==2,
∴OC=OB=,
∵=,即,解得BE=,
∴CE=,
∵Rt△DCE与Rt△DOC有公共角∠D,
∴Rt△DCE~Rt△DOC,
∴=,即DC2=DO DE=(+BD)(+BD),
在Rt△DOC中有:DC2+OC2=OD2,
即(+BD)(+BD)+=(+BD)2,
解得BD=,
∴DC==.
(3)如图,作点O关于AC的对称点O′,连接AO′,CO′,OC,O′M,过点M作MH⊥AO于H.过点O′作O′P⊥AB于P.
∵tan∠MAH==,
∴MH=AM,
∵MO=MO′,
∴OM+AM=O′M+MH≤O′P,
∴当M,H在O′P上时,OM+AM的值最小,最小值为线段O′P的长,
∵OA=OC=AO′=CO′,
∴四边形AOCO′是菱形,
∴S菱形AOCO′= AC OO′=AO PO′,
∴PO′==,
故OM+AM的最小值为.
18.如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若tan∠ADC=,AC=2,求⊙O的半径;
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
【解答】解:(1)CD与⊙O相切,理由:
如图1,连接OD,
∵OB=OD,
∴∠ODB=∠CBD,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB为⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDA+∠ADO=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD与⊙O相切;
(2)由(1)知,∠CBD=∠ADC,
∵tan∠ADC=,
∴tan∠CBD=,
在Rt△ADB中,tan∠CBD==,
∵∠C=∠C,∠ADC=∠CBD,
∴△CAD∽△CDB,
∴,
∴CD=2CA=4,
∴CB=2CD=8,
∴AB=CB﹣CA=8﹣2=6,
∴OA=OB=AB=3;
(3)如图2,连接OE,过点E作EG⊥BD于G,
∵DE平分∠ADB,
∴∠ADE=∠BDE=45°,
∴∠BOE=2∠BDE=90°,
∴BE==3,
在Rt△ABD中,AD2+BD2=AB2=62,
∵,
∴AD=,BD=,
∵EG⊥BD,∠BDE=45°,
∴∠DEG=∠BDE=45°,
∴DG=EG,
设DG=EG=x,则BG=BD﹣DG=﹣x,
在Rt△BEG中,EG2+BG2=BE2=(3)2=18,
∴x2+(﹣x)2=18,
∴x=或x=(舍),
∴EG=,
∴sin∠DBE==.
19.如图1,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.
(1)求证:△ADG∽△CFG.
(2)若G是的中点,当CG与△ADE的一边平行时,求的值.
(3)如图2,点E是OB的中点,AB=8,连接BG,BD,BC.当DG+CG=6时,求cosF的值.
【解答】解:(1)∵四边形AGCD为⊙O的内接四边形,
∴∠AGC+∠ADC=180°,∠DAG+∠DCG=180°,
∵∠AGC+∠CGF=180°,∠DCG+∠GCF=180°,
∴∠CGF=∠ADC,∠DAG=∠GCF,
∴△ADG∽△CFG;
(2)①当CG∥AD时,
∵G是的中点,
∴
∴AG=CG,
则△ADG≌△CFG(AAS),
∴∠ADG=∠F,∠DAG=∠DAG,
∴△DAG∽△AFD,
∴,
设CF=x,AG=y,
∴,
解得x=y,
∴;
②当CD∥AE时,
∴∠GCF=90°
∵∠DOB=∠AOG,
∴,
∴,
∴∠AOG=60°,
∴∠GDA=∠F=30°,
∴=tanF=tan30°=;
(3)延长CD至点M,使DM=CG,连BM,过B作BN⊥MG,连OD,
∵MD=CG,∠MDB=∠BCG,BD=BC,
∴△MDB≌△GCB(SAS),
∴BM=GB,
∵E为OB中点,CD⊥AB,
∴OD=BD=OB,
∴△BDO为等边三角形,
∴∠DOB=60°,
∴∠DGB=30°,
∴GM=DG+DM=DG+GC=6,
∴GN=GM=3,GB=6,
由(1)得,∠F=∠ADG=∠ABG,
在Rt△ABG中,cosF=cos∠ABG=.
20.如图,四边形BCDE是⊙O的内接四边形,DE是⊙O的直径,BC、ED的延长线交于点A,连接CE、BD交于点F,DF2=FC FE,点H是线段CE上一点连接BH、DH.
(1)求证:DF=BF;
(2)若∠BEC=∠DBH,∠BDE=45°,求;
(3)在(2)的条件下,若AE=AC,CB+DE=2+2.求线段AC的长度.
【解答】(1)证明:∵∠BCE=∠EDB,∠CBD=∠DEC,
∴△BCF∽△EDF,
∴=,
∴DF BF=FC FE,
∵DF2=FC FE,
∴DF2=DF BF,
∴DF=BF;
(2)解:∵∠BEC=∠BDC,∠BEC=∠DBH,
∴∠BEC=∠BDC=∠DBH,
∴CD∥BH,
∴△CFD∽△HFB,
∴=,
∵DF=BF,
∴CF=HF,
∴四边形CDHB是平行四边形,
∴BC∥DH,
∴∠DHC=∠BCE=∠BDE=45°,∠BHC=∠DCE=90°,
∴△DHC、△BHC是等腰直角三角形,
∴=,
∵CF=HF,
∴CH=2CF,
∴=2;
(3)解:∵四边形CDHB是平行四边形,
∴HD∥BC,HD=BC,CD∥BH,CD=BH,
∴=,
∴,
∵AE=AC,
∴DE=DH,
∵CB+DE=2+2.
∵HD=BC,
∴DH+DH=2+2.
解得:DH=2,
∴DE=2.
∵△DHC、△BHC是等腰直角三角形,
∴CD=CH=BH=,BE=,
∵∠CHB=90°,
∴∠EHB=90°,
∴EH==2,
∴CE=CH+EH=3,
∵四边形BCDE是⊙O的内接四边形,
∴∠CDE+∠EBC=180°,
∵∠CDE+∠ADC=180°,
∴∠ADC=∠EBC,
∵∠DCE=90°,∠BCE=45°,
∴∠ACD=∠ECB=45°,
∴△ACD∽△ECB,
∴,即=,
∴AC=3.
21.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,连接OA、OB、OC,延长BO与AC交于点D,与⊙O交于点F,延长BA到点G,使得∠BGF=∠GBC,连接FG.
(1)求证:FG是⊙O的切线;
(2)若⊙O的半径为3.
①当OD=2,求AD的长度;
②当△OCD是直角三角形时,求△ABC的面积.
【解答】(1)证明:连接AF,
∵BF为⊙O的直径,
∴∠BAF=90°,∠FAG=90°,
∴∠BGF+∠AFG=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠AFB,∠BGF=∠ABC,
∴∠BGF=∠AFB,
∴∠AFB+∠AFG=90°,即∠OFG=90°,
∴OF⊥FG,
又∵OF为半径,
∴FG是⊙O的切线;
(2)解:①连接CF,则∠ACF=∠ABF,
∵AB=AC,AO=AO,BO=CO,
∴△ABO≌△ACO(SSS),
∴∠ABO=∠BAO=∠CAO=∠ACO,
∴∠CAO=∠ACF,
∴AO∥CF,
∴=,
∵半径是3,OD=2,
∴DF=OF﹣OD=1,BD=OB+OD=5,
∴==2,即CD=AD,
∵∠ABD=∠FCD,∠ADB=∠FDC,
∴△ADB∽△FDC,
∴=,
∴AD CD=BD DF,
∴AD CD=5,即AD2=5,
∴AD=(负值舍去);
②∵△ODC为直角三角形,∠DCO不可能等于90°,
∴存在∠ODC=90°或∠COD=90°,
当∠ODC=90°时,
由①知∠ACO=∠ACF,
∴OD=DF=,BD=,
∵OD⊥AC,
∴AD=CD,
由①可知AD CD=BD DF,
∴AD CD=AD2=×=,
∴AD=,
∴AC=2AD=3,
∴S△ABC=×AC×BD=×3×=;
当∠COD=90°时,
∵OB=OC=3,
∴△OBC是等腰直角三角形,
∴BC=3,
延长AO交BC于点M,则AM⊥BC,
∴MO=,
∴AM=3+,
∴S△ABC=×BC×AM=×3×(3+)=,
∴△ABC的面积为或.
22.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切:
(2)若,求的值;
(3)在(2)的条件下,若⊙O的半径为4,PD=OD,求EC的长.
【解答】(1)证明:如图,连接OB,则OB=OD,
∴∠BDC=∠DBO,
∵∠BAC=∠BDC、∠BDC=∠GBC,
∴∠GBC=∠BDC,
∵CD是⊙O的直径,
∴∠DBO+∠OBC=90°,
∴∠GBC+∠OBC=90°,
∴∠GBO=90°,
∴PG与⊙O相切;
(2)解:过点O作OM⊥AC于点M,连接OA,
则∠AOM=∠COM=∠AOC,
∵=,
∴∠ABC=∠AOC,
又∵∠EFB=∠OMA=90°,
∴△BEF∽△OAM,
∴=,
∵AM=AC,OA=OC,
∴=,
又∵=,
∴=2×=2×=2×=;
(3)解:∵PD=OD,∠PBO=90°,
∴BD=OD=4,
在Rt△DBC中,BC===4,
又∵OD=OB,
∴△DOB是等边三角形,
∴∠DOB=60°,
∵∠DOB=∠OBC+∠OCB,OB=OC,
∴∠OCB=30°,
∴=,=,
∴可设EF=x,则EC=2x、FC=x,
∴BF=4﹣x,
∵=,且OC=4,
∴BE=5,
在Rt△BEF中,BE2=EF2+BF2,
∴100=x2+(4﹣x)2,
解得:x=6±,
∵>4,舍去,
∴x=,
∴EC=6﹣,
∴OE=4﹣(6﹣)=﹣2.
23.如图,在△ABC中,∠A=90°,D是边AC上一动点,且不与A,C两点重合,连接BD,过点D作DE⊥BD交边BC于点E,△BDE的外接圆交边AB于另一点F,连接DF.
(1)求证:△ADF∽△DBE.
(2)当AB=6,AC=8时.
①若AD=3AF,求AD的长.
②当线段DE,DF,BF中有两条相等时,求出所有符合条件的tan∠ADF的值.
(3)若BD平分∠ABC,S△ADF=1,S△BDE=6,则S△CDE= .
【解答】解:(1)证明:∵四边形FBED为圆内接四边形,
∴∠DFA=∠DEB,
∵DE⊥BD,
∴∠EDB=∠A=90°,
∴△ADF∽△DBE;
(2)连接EF,
①设AF=t,AD=3t,
则BF=6﹣t,BD=,
∵∠EDB=90°,
∴EB为直径,
∴∠EFB=∠A=90°,
∵∠EBF=∠CBA,
∴△EFB∽△CAB,
∴=,
∴BE=(6﹣t),
∵△ADF∽△DBE,
∴=,
∴=,
整理得,13t2+60t﹣108=0,
解得,t=或t=﹣6(舍去),
∴AD=3t=.
②设AF=t,tan∠ADF=m,
则AD=,DB=,BE=(6﹣t),
1°.当BF=DF=6﹣t时,
∵△ADF∽△DBE;
∴=,
∴=,
解得m=t,
∴AD=,
在Rt△ADF中,由勾股定理得,
AF2+AD2=FD2,
即t2+()2=(6﹣t)2,
解得t=,
∴tan∠ADF=m=t=;
2°.当DF=DE=时,
∵△ADF∽△DBE;
∴=,
∴=,
=10t﹣t2①,
在Rt△BDE中,由勾股定理得,
BD2+DE2=BE2,
即36+++t2=[(6﹣t)]2②,
将①代入②得,
36+10t﹣t2+10t﹣t2+t2=[(6﹣t)]2,
整理得,2t2﹣15t+18=0
解得t=6(舍去)或t=,
将t=代入①得,
m2=,
∴m=;
3°.当BF=DE=6﹣t时,
∵BE=BE,
∴Rt△EFB≌Rt△BDE(HL),
∴∠DBE=∠FEB,
∵△ADF∽△DBE,
∴∠ADF=∠DBE,
∴∠ADF=∠FEB,
∵∠EFB=∠A=90°
∴EF∥AC,
∴∠FEB=∠ACB,
∴∠ADF=∠ACB,
∴tan∠ADF=tan∠ACB==,
综上所有符合条件的tan∠ADF的值为:或或;
(3)设AF=t,
∵S△ADF=AF AD=1,
∴AD=,
∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ADF,
∴△ADF∽△ABD,
∴=,
∴AB=,
∴BF=﹣t,
∵△ADF∽△DBE,
∴=()2=()2=,
∴BD=AD=,
BE=DF=×,
在Rt△ABD中,由勾股定理得,
AD2+AB2=BD2,
即()2+()2=()2,
t4=,
∵△EFB∽△CAB,
∴=,
∴BC====4××=×,
∴AC2=BC2﹣AB2=(×)2﹣()2=(t2+)﹣=×(+4×)﹣16×()3=,
AB2=()2=16×()3=10,
∴AC2 AB2=10×=625,
∴S△ABC=AB AC=,
∵△ADF∽△ABD,
∴=()2==,
∴S△ADB=5S△ADF=5,
∴S△CDE=S△ABC﹣S△ADB﹣S△BDE=﹣5﹣6=.
24.如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
【解答】(1)证明:如图1中,连接BC.
∵=,
∴∠DCB=∠DBC,
∵AB是直径,
∴∠ACB=∠BCE=90°,
∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,
∴CD=ED.
(2)①证明:如图2中,
∵CF=CH,
∴∠CFH=∠CHF,
∵∠AFO=∠CFH,
∴∠AFO=∠CHF,
∵=,
∴∠CAD=∠BAD,
∴△AFO∽△AHC,
∴=,
∴=,
∴CF AF=OF AH.
②解:如图3中,连接OD交BC于G.设OG=x,则DG=2﹣x.
∵=,
∴∠COD=∠BOD,
∵OC=OB,
∴OD⊥BC,CG=BG,
在Rt△OCG和Rt△BGD中,则有22﹣x2=12﹣(2﹣x)2,
∴x=,即OG=,
∵OA=OB,
∴OG是△ABC的中位线,
∴OG=AC,
∴AC=.
25.如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为,△ABC的面积为2,求CD的长;
(3)在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若=,求BF的长.
【解答】(1)证明:连接OC,如图:
∵AB为⊙O的直径,
∴∠ACB=90°,∠A+∠ABC=90°,
∵OB=OC,
∴∠ABC=∠BCO,
又∠BCD=∠A,
∴∠BCD+∠BCO=90°,即∠DCO=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)过C作CM⊥AB于M,过B作BN⊥CD于N,如图:
∵⊙O的半径为,
∴AB=2,
∵△ABC的面积为2,
∴AB CM=2,即×2 CM=2,
∴CM=2,
Rt△BCM中,∠BCM=90°﹣∠CBA,
Rt△ABC中,∠A=90°﹣∠CBA,
∴∠BCM=∠A,
∴tan∠BCM=tanA,即=,
∴=,
解得BM=﹣1,(BM=+1已舍去),
∵∠BCD=∠A,∠BCM=∠A,
∴∠BCD=∠BCM,
而∠BMC=∠BNC=90°,BC=BC,
∴△BCM≌△BCN(AAS),
∴CN=CM=2,BN=BM=﹣1,
∵∠DNB=∠DMC=90°,∠D=∠D,
∴△DBN∽△DCM,
∴==,
即==,
解得DN=2﹣2,
∴CD=DN+CN=2;
方法二:过C作CM⊥AB于M,连接OC,如图:
∵⊙O的半径为,
∴AB=2,
∵△ABC的面积为2,
∴AB CM=2,即×2 CM=2,
∴CM=2,
Rt△MOC中,OM==1,
∵∠DMC=∠CMO=90°,∠CDM=90°﹣∠DCM=∠OCM,
∴△DCM∽△COM,
∴=,即=,
∴CD=2;
(3)过C作CM⊥AB于M,过E作EH⊥AB于H,连接OE,如图:
∵CM⊥AB,EH⊥AB,
∴==,
∵=,
∴==,
由(2)知CM=2,BM=﹣1,
∴HE=1,MF=2HF,
Rt△OEH中,OH===2,
∴AH=OA﹣OH=﹣2,
设HF=x,则MF=2x,
由AB=2可得:BM+MF+HF+AH=2,
∴(﹣1)+2x+x+(﹣2)=2,
解得:x=1,
∴HF=1,MF=2,
∴BF=BM+MF=(﹣1)+2=+1.
26.如图1,以△ABC的边AC为直径作⊙O交BC于点D,连接AD,点E为AD上一点(不与端点重合),连接CE,作DF⊥CE于点F,延长DF交AC于点M,交BA的延长线于点G,∠BGD=∠ACE.
(1)求证:BG是⊙O的切线;
(2)求证:;
(3)如图2,延长CE交AB于点H,若HE=4,∠ACH=∠BCH,sin∠BGD=,求BC的长.
【解答】解:(1)∵∠BGD=∠ACE,且∠AMG=∠CMF,
∴180°﹣∠BGD﹣∠AMG=180°﹣∠ACE﹣∠CMF,即∠GAM=∠CFM,
∵DF⊥CE,
∴∠GAM=∠CFM=90°,
∴OA⊥BG,
∴BG是⊙O的切线;
(2)∵AC为⊙O直径,
∴∠ADC=∠ADB=90°,
∵OA⊥BG,
∴∠B=90°﹣∠ACB=∠DAC,
∴△ADB∽△CDA,
∴=,
∴AB AD=AC BD,
∵∠B=∠DAC,∠BGD=∠ACE,
∴△BGD∽△ACE,
∴=,
∴AC BD=BG AE,
∴AB AD=BG AE,
∴;
(3)设CH交⊙O于N,连接AN,如图:
∵AC为⊙O直径,
∴∠ADC=90°=∠ANC,
∵DF⊥CE,
∴∠FCD=90°﹣∠FDC=∠EDF,AN∥DG,
∴∠BGD=∠HAN,∠NAD=∠ADG,
∵∠ACH=∠BCH,∠BGD=∠ACE,
∴∠ACH=∠BCH=∠EDF=∠BGD=∠HAN=∠NAD,
在△AHN和△AEN中,
∴△AHN≌△AEN(ASA),
∴HN=EN=HE,AH=AE,
∵HE=4,
∴HN=EN=2,
∵sin∠BGD=,
∴sin∠HAN=,
Rt△AHN中,=可得AH=5=AE,
Rt△AHC中,sin∠ACH=sin∠BGD=,
∴=,可得CH=,
∴AC==,EC=CH﹣HE=,
∵∠B=∠DAC,∠ACE=∠BCH,
∴△AEC∽△BHC,
∴=,
∴=,
∴BC=.
27.如图,点I是O△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)求证:DG是⊙O的切线;
(2)若DE=4,BE=5,求DI的长;
(3)若sin∠ACD=,CD=10,求△ACD的内心到点O的距离.
【解答】(1)证明:连接OD.
∵点I是△ABC的内心,
∴∠CBD=∠ABD,
∴=,
∴OD⊥AC,DC=DA,
∴∠ODA=∠CDA,
∵DG平分∠ADF,
∴∠ADG=∠ADF,
∴∠ODG=∠ODA+∠ADG=(∠CDA+∠ADF)=90°,
∴OD⊥DG,
∴DG是⊙O的切线.
(2)解:∵点I是△ABC的内心,
∴∠BAI=∠CAI,
∵∠EIA=∠IBA+∠IAB=∠CAD+∠CAI,
即∠DIA=∠DAI,
∴DA=DI,
∵∠DAE=∠DBA,∠ADE=∠BDA,
∴△DAE∽△DBA,
∴AD:DB=DE:DA,
即AD:9=4:AD,
∴AD=6,
∴DI=6.
(3)解:如图,连接OD交AC于T,设G是△ACD的内心,连接CG,OC.
∵DC=DA,OD⊥AC,
∴OD平分∠CDA,
∴△ACD的内心在DT上,
在Rt△CDT中,CD=10,sin∠DCT==,
∴DT=6,
∴CT=AT===8,
设OD=OC=x,
在Rt△OCE中,则有x2=82+(x﹣6)2,
∴x=,
∴OT=﹣6=,
∵G是△ACD的内心,
∴ (CD+AD+AC) GT= AC DT,
∴GT==,
∴OG=OT+GT=+=5.
∴△ACD的内心到点O的距离为5.
28.如图,以Rt△ABC的斜边AC为直径作⊙O,点D在半径OC上,过点D作AC的垂线,分别交弦BC于点E,交⊙O于F.在射线DE上取点G,连接GB并延长交CA的延长线于点H,且满足GB=GE.
(1)求证:HG是⊙O的切线;
(2)若GE=BE,HB=.
(i)求⊙O的半径;
(ii)如图2,连接AF,交弦BC于点M,若AF∥HG,求线段OD的长.
【解答】解:(1)连接OB,如图:
∵GB=GE,
∴∠GBE=∠GEB=∠CED,
∵GD⊥AC,
∴∠CED+∠ECD=90°,
∴∠GBE+∠ECD=90°,
∵OB=OC,
∴∠ECD=∠OBC,
∴∠GBE+∠OBC=90°,
∴OB⊥HG,
∴HG是⊙O的切线;
(2)(i)过G作GM⊥BC于M,如图:
∵GB=GE,GM⊥BC,
∴ME=BE,
∵GE=BE
∴=,
∴cos∠GEM=,
∴cos∠CED=,
∵AC为⊙O直径,
∴∠ABC=90°,
∴∠BAC=90°﹣∠C=∠CED,
∴cos∠BAC=,
设AB=k,则AC=k,BC=2k,
∵HG为⊙O切线,
∴∠C=∠HBA,
而∠H=∠H,
∴△HBA∽△HCB,
∴====,
∵HB=,
∴HC=,HA=,
∴AC=HC﹣HA=2,
∴⊙O的半径为;
(ii)连接CF,过F作FN⊥BC于N,如图:
由(i)知:AC=2,cos∠BAC=,
∴AB=2,BC=4,
∵AF∥HG,
∴∠AMB=∠GBC,
∵GB=GE,
∴∠GBC=∠GEM,
∴∠AMB=∠GEM,
∴cos∠AMB=cos∠GEM=,
Rt△ABM中,设BM=t,则AM=t,AB=2t,
∴2t=2,解得t=1,
∴BM=1,AM=,
∴CM=BC﹣BM=3,
∵BC与AF是⊙O的相交弦,
∴AM MF=BM CM,即 MF=1×3,
∴MF=,
Rt△FNM中,cos∠FMN=cos∠AMB=,
∴=,
∴MN=,ME=,
∴CE=CM﹣ME=,
Rt△CED中,cos∠CED=cos∠GEB=,
∴ED=,CD=,
∴OD=OC﹣CD=.
29.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E,连接AD,CD.
(1)求证:DE与⊙O相切;
(2)若AB=6,tanA=,求BE的长;
(3)线段AB,BE,CE之间有何数量关系?写出你的结论并证明.
【解答】(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE,
∵BE⊥DE,
∴OD⊥DE,
∴DE与⊙O相切.
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=6,tanA=,
∴BD=AD,
设AD=m,则BD=m,
∴m2+2m2=36,
∴m=2或﹣2(舍弃),
∴AD=2,BD=2,
∵BE⊥DE,
∴∠ADB=∠BED=90°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴△ABD∽△DBE,
∴=,
∴=,
∴BE=4.
(3)解:结论CE=AB﹣BE,
理由:过D作DH⊥AB于H,
∵BD平分∠ABC,DE⊥BE,
∴DH=DE,
在Rt△BED与Rt△BHD中,
,
∴Rt△BED≌Rt△BHD(HL),
∴BH=BE,
∵∠DCE=∠A,∠DHA=∠DEC=90°,
∴△ADH≌△CDE(AAS),
∴AH=CE,
∵AB=AH+BH,
∴AB=BE+CE,
∴CE=AB﹣BE.
30.如图,AB是⊙O的直径,AC是弦,点E在圆外,OE⊥AC于点D,BE交⊙O于点F,连接BD、BC、CF,∠BFC=∠AED.
(1)求证:AE是⊙O的切线;
(2)求证:OB2=OD OE;
(3)设△BAD的面积为S1,△BDE的面积为S2,若tan∠ODB=,求的值.
【解答】解:(1)证明:∵∠BFC=∠AED,
又∠BFC=∠BAC,
∴∠BAC=∠AED,
∵OE⊥AC于点D,
∴∠ADE=∠ADO=90°,
∴∠AED+∠EAD=90°,
∴∠BAC+∠EAD=90°,即∠OAE=90°,
∴OA⊥AE,
∴AE是⊙O的切线;
(2)∵∠OAE=∠ADO=90°,∠AOD=∠EOA,
∴△AOD∽△EOA,
∴,
∴OA2=OD OE,
∵OB=OA,
∴OB2=OD OE;
(3)∵AB为直径,
∴∠ACB=90°,
∵∠ADO=90°,
∴∠ACB=∠ADO,
∴OE∥BC,
∴∠ODB=∠DBC,
在Rt△BCD中,tan∠DBC=tan∠ODB==,
设DC=2m,则BC=3m,
∴OD=BC=,
∵OE⊥AC于点D,
∴AD=DC=2m,
∴OA=OB==,
由(2)知OB2=OD OE,
∴,
而∠BOD=∠EOB,
∴△BOD∽△EOB,
∴,
∴设S△BOD=9k,则S△EOB=25k,
∴△BDE的面积为S2=S△EOB﹣S△BOD=16k,
而△BAD的面积为S1=2S△BOD=18k,
∴==.
31.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)求证:AF为⊙O的切线;
(2)当点D为EF的中点时,求证:AD2=AO AE;
(3)在(2)的条件下,若sin∠BAC=,AF=2,求BF的长.
【解答】(1)证明:连接CD.
∵AC是直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∵∠ABD=∠ACD,∠DAF=∠ABD,
∴∠DAF=∠ACD,
∴∠DAF+∠DAC=90°,
∴∠FAC=90°,
∴AF为⊙O的切线.
(2)证明:∵∠FAE=90°,DF=DE,
∴AD=DE=DF,
∴∠DAE=∠AED,
∵OA=OD,
∴∠DAE=∠ADO,
∴∠ADO=∠AED,
∵∠OAD=∠DAE,
∴△ADO∽△AED,
∴=,
∴AD2=AO AE.
(3)解:过点B作BJ⊥EC于J.
∵AC是直径,
∴∠ABC=90°,
∴sin∠BAC==,
∴可以假设BC=a,AC=3a,
∵BJ⊥AC,
∴∠AJB=90°,
∴∠BAC+∠ABJ=90°,∠ABJ+∠CBJ=90°,
∴∠CBJ=∠BAC,
∴sin∠CBJ=sin∠BAC==,
∴CJ=a,
∴BJ===a,
∵DA=DE,
∴∠DAE=∠AED=∠CEB,
∵∠DAE=∠CBE,
∴∠CEB=∠CBE,
∴CE=CB=a,
∴EJ=EC﹣CJ=a﹣a=a,AE=AC﹣EC=2a,
∵AF∥BJ,
∴=,
∴=,
∴a=,
∴AE=2,EJ=,BJ=,
∴EF===6,BE===2,
∴BF=EF+BE=6+2=8.
32.如图1,O是△ABC的边BC的中点,⊙O与BC交于E、F两点,与AB相切于点D,连接AO交⊙O于点P,=.
(1)猜想AC与⊙O的位置关系,并证明你的猜想.
(2)如图2,延长AO交⊙O于Q点,连接DE、DF,DQ,FQ,FQ=,ED=5,求DQ的长.
(3)如图3,若DE=5,连接DF、DP、PF,设DP=x,△DPF的面积为y,求y与x之间的函数关系式.
【解答】解:(1)结论:AC与⊙O相切,
理由:过点O作OH⊥AC于H,
∵⊙O与AB相切于点D,
∴OD⊥AB,
∵,点O是圆心,
∴∠BOP=∠COP=90°,
又∵O是BC的中点,
∴AB=AC,
∴∠BAO=∠OAC,
又∵OD⊥AB,OH⊥AC,
∴OD=OH,
∴OH是半径,
∴AC与⊙O相切.
(2)如图2中,过点Q作QN⊥CD于N,QM⊥DE交DE的延长线于M,连接QE.
∵AO⊥BC,O是圆心,
∴PQ是直径,
∴OQ=OF,
∴FQ=OF=,
∴FO=,
∴EF=13,
∵EC是直径,
∴∠EDC=90°,
∵FD2=EF2﹣DE2,DE=5,
∴FD=12,
∵∠QDF=∠QOF=45°,
∴∠QDM=∠QDN=45°,
∴=,
∴EQ=FQ,
∵QM⊥DM,QN⊥DN,
∴QM=QN,
∵∠M=∠QNF=90°,
∴Rt△QME≌Rt△QNF(HL),
∴EM=FN,
∵∠M=∠MDN=∠DNQ=90°,
∴四边形DMQN是矩形,
∵QM=QN,
∴四边形DMQN是正方形,
∴DM=DN,
∴DE+DF=DM﹣EM+DN+NF=2DM=17,
∴DM=DN=,
∴DQ=DN=.
(3)如图3中,过点F作FH⊥DP交DP的延长线于H.
∵∠PDF=∠POC=45°,∠H=90°,
∴∠HDF=∠DFH=45°,
∴DH=FH,DF=FH,
∵∠EDF=∠H=90°,∠EFP=∠DFH=45°,
∴∠EFD=∠PFH,
∴△EFD∽△PFH,
∴==,
∵DE=5,
∴PH=,
∴DH=FH=x+,
∴y=S△PDF= DP FH,
∴y=×x×(x+)=x2+x(x>0).
33.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD∥AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:AF是⊙O的切线;
(2)求证:AB2﹣BE2=BE EC;
(3)如图2,若点G是△ACD的内心,BC BE=64,求BG的长.
【解答】解:(1)如图1,连接OA,
∵AB=AC,
∴=,∠ACB=∠B,
∴OA⊥BC,
∵CA=CF,
∴∠CAF=∠CFA,
∵CD∥AB,
∴∠BCD=∠B,
∴∠ACB=∠BCD,
∴∠ACD=∠CAF+∠CFA=2∠CAF,
∵∠ACB=∠BCD,
∴∠ACD=2∠ACB,
∴∠CAF=∠ACB,
∴AF∥BC,
∴OA⊥AF,
∴AF为⊙O的切线;
(2)∵∠BAD=∠BCD=∠ACB,∠B=∠B,
∴△ABE∽△CBA,
∴,
∴AB2=BC BE=BE(BE+CE)=BE2+BE CE,
∴AB2﹣BE2=BE EC;
(3)由(2)知:AB2=BC BE,
∵BC BE=64,
∴AB=8,
如图2,连接AG,
∴∠BAG=∠BAD+∠DAG,∠BGA=∠GAC+∠ACB,
∵点G为内心,
∴∠DAG=∠GAC,
又∵∠BAD=∠ACB,
∴∠BAD+∠DAG=∠GAC+∠ACB,
∴∠BAG=∠BGA,
∴BG=AB=8
1.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式;
②如图②,连接OE,OD,若=,求y的值.
2.已知AB、CD为⊙O的两条弦,AB∥CD.
(1)如图1,求证弧AC=弧BD;
(2)如图2,连接AC、BC、OA、BD,弦BC与半径OA交于点G,延长AO交CD于点E,连接BE,使BE=BD,若OA⊥BC,求证:四边形ABEC为菱形;
(3)在(2)的条件下,CH与⊙O相切于点C,连接CO并延长交BE于点F,延长BE交CH于点H,OF=11,sin∠BDC=,求CH长.
3.如图,以Rt△BCE的直角边BC为直径作⊙O,交斜边EC于点A,AD⊥BC于点D,点F是BE的中点,连接CF与AD相交于点G,延长AF与CB的延长线相交于点P.
(1)求证:PA是⊙O的切线;
(2)求证:点G为AD的中点;
(3)若2FG=EB,且⊙O的半径长为3,求BD的长度.
4.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC;
②若CM=10,tan∠CMO=2,求ON的长.
5.如图,AB是⊙O的直径,C、D是⊙O上两点.AE与过点C的切线垂直,垂足为E,直线EC与直径AB的延长线相交于点P,弦CD交AB于点F,连接AC、AD、BC、BD.
(1)若∠ABC=∠ABD=60°,判断△ACD的形状,并证明你的结论;
(2)若CD平分∠ACB,求证:PC=PF;
(3)在(2)的条件下,若AD=5,PF=5,求由线段PC、和线段BP所围成的图形(阴影部分)的面积.
6.已知四边形ABCD内接于⊙O,AB=AD.
(1)如图1,求证:点A到∠C两边的距离相等;
(2)如图2,已知BD与AC相交于点E,BD为⊙O的直径.①求证:tan∠CAD=;②若∠CBD=30°,AD=,求AE的长.
7.如图,⊙O的内接四边形ABCD的两条对角线相交于点E,两组对边的延长线分别相交于点F,G,且∠F=67.5°,∠G=22.5°,=,边AB过圆心O.
(1)求∠BAD的度数;
(2)求∠BAC的正切值;
(3)若AB=2,则CE CA的值等于多少?
8.如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
(1)求证:PE是⊙O的切线;
(2)试判断△AEF的形状,并说明理由;
(3)若AF=2,AE=,求OA的长.
9.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积;
(4)在(3)的条件下,求的长度.
10.如图,点B是⊙C上的一点,点A是直径ED延长线上的一点,连接AB,EB,BD,且∠ABD=∠E.
(1)求证:直线AB是⊙C的切线;
(2)当时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=4,求⊙C的半径.
11.如图1,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交BC于E,连接AE交CD于G,交⊙O于F,连接DF,∠BAC=∠EFD.
(1)求证:AB与⊙O相切;
(2)如图2,若AF:FG=3:2,
①若AF=6,求线段CG的长;
②求tan∠CAE的值.
12.如图,AB、CD都是⊙O的直径,连接AD,BC.
(1)求证:AD=BC;
(2)过D点作⊙O的切线DE交BA的延长线于点E,F是BE上一点,连接CF交⊙O于点M,若ED=CF,求证:∠BED=∠CFB.
(3)在(2)的条件下,连接DM交EB于点N,连接CN,若tan∠CNO=,ON=2,求DE的长.
13.如图,AB是⊙O的直径,点C在⊙O上,且AB=2,=,D是⊙O上一动点,连接BD,过点B作BE⊥BD交直线DC于点E.
(1)当点D是的中点时,求△BCD的面积;
(2)过点B作BF⊥DE于点F,求的值;
(3)在点D运动过程中,求线段AE的最大值.
14.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=,求⊙O的半径.
15.如图,在Rt△ABC中,∠C=90°,O为AB上一点,以点O为圆心,OA为半径作⊙O,分别交AB、AC于点E、F,且与BC相切于点D,连接OF.解答下列问题:
(1)∠BAC与∠OFA之间的关系是 ;
(2)求证:∠AFO=2∠BAD;
(3)若=,求tan的值.
16.如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=3,EF=5,
①求证:DE=EF;
②求⊙O的半径.
17.如图,⊙O是△ABC的外接圆,AB是的直径,D是AB延长线上的一点,连接DC,∠DCB=∠A,CE⊥AB于点E.
(1)求证DC是⊙O的切线;
(2)若AC=4,tan∠BCE=,求DC的长;
(3)在(2)的条件下,若M是线段AC上一动点,求OM+AM的最小值.
18.如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若tan∠ADC=,AC=2,求⊙O的半径;
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
19.如图1,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.
(1)求证:△ADG∽△CFG.
(2)若G是的中点,当CG与△ADE的一边平行时,求的值.
(3)如图2,点E是OB的中点,AB=8,连接BG,BD,BC.当DG+CG=6时,求cosF的值.
20.如图,四边形BCDE是⊙O的内接四边形,DE是⊙O的直径,BC、ED的延长线交于点A,连接CE、BD交于点F,DF2=FC FE,点H是线段CE上一点连接BH、DH.
(1)求证:DF=BF;
(2)若∠BEC=∠DBH,∠BDE=45°,求;
(3)在(2)的条件下,若AE=AC,CB+DE=2+2.求线段AC的长度.
21.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,连接OA、OB、OC,延长BO与AC交于点D,与⊙O交于点F,延长BA到点G,使得∠BGF=∠GBC,连接FG.
(1)求证:FG是⊙O的切线;
(2)若⊙O的半径为3.
①当OD=2,求AD的长度; ②当△OCD是直角三角形时,求△ABC的面积.
22.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切:
(2)若,求的值;
(3)在(2)的条件下,若⊙O的半径为4,PD=OD,求EC的长.
23.如图,在△ABC中,∠A=90°,D是边AC上一动点,且不与A,C两点重合,连接BD,过点D作DE⊥BD交边BC于点E,△BDE的外接圆交边AB于另一点F,连接DF.
(1)求证:△ADF∽△DBE.
(2)当AB=6,AC=8时.
①若AD=3AF,求AD的长.
②当线段DE,DF,BF中有两条相等时,求出所有符合条件的tan∠ADF的值.
(3)若BD平分∠ABC,S△ADF=1,S△BDE=6,则S△CDE= .
24.如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
25.如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为,△ABC的面积为2,求CD的长;
(3)在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若=,求BF的长.
26.如图1,以△ABC的边AC为直径作⊙O交BC于点D,连接AD,点E为AD上一点(不与端点重合),连接CE,作DF⊥CE于点F,延长DF交AC于点M,交BA的延长线于点G,∠BGD=∠ACE.
(1)求证:BG是⊙O的切线;
(2)求证:;
(3)如图2,延长CE交AB于点H,若HE=4,∠ACH=∠BCH,sin∠BGD=,求BC的长.
27.如图,点I是O△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)求证:DG是⊙O的切线;
(2)若DE=4,BE=5,求DI的长;
(3)若sin∠ACD=,CD=10,求△ACD的内心到点O的距离.
28.如图,以Rt△ABC的斜边AC为直径作⊙O,点D在半径OC上,过点D作AC的垂线,分别交弦BC于点E,交⊙O于F.在射线DE上取点G,连接GB并延长交CA的延长线于点H,且满足GB=GE.
(1)求证:HG是⊙O的切线;
(2)若GE=BE,HB=.
(i)求⊙O的半径;
(ii)如图2,连接AF,交弦BC于点M,若AF∥HG,求线段OD的长.
29.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E,连接AD,CD.
(1)求证:DE与⊙O相切;
(2)若AB=6,tanA=,求BE的长;
(3)线段AB,BE,CE之间有何数量关系?写出你的结论并证明.
30.如图,AB是⊙O的直径,AC是弦,点E在圆外,OE⊥AC于点D,BE交⊙O于点F,连接BD、BC、CF,∠BFC=∠AED.
(1)求证:AE是⊙O的切线;
(2)求证:OB2=OD OE;
(3)设△BAD的面积为S1,△BDE的面积为S2,若tan∠ODB=,求的值.
31.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)求证:AF为⊙O的切线;
(2)当点D为EF的中点时,求证:AD2=AO AE;
(3)在(2)的条件下,若sin∠BAC=,AF=2,求BF的长.
32.如图1,O是△ABC的边BC的中点,⊙O与BC交于E、F两点,与AB相切于点D,连接AO交⊙O于点P,=.
(1)猜想AC与⊙O的位置关系,并证明你的猜想.
(2)如图2,延长AO交⊙O于Q点,连接DE、DF,DQ,FQ,FQ=,ED=5,求DQ的长.
(3)如图3,若DE=5,连接DF、DP、PF,设DP=x,△DPF的面积为y,求y与x之间的函数关系式.
33.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD∥AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:AF是⊙O的切线;
(2)求证:AB2﹣BE2=BE EC;
(3)如图2,若点G是△ACD的内心,BC BE=64,求BG的长.
答案与解析
1.如图①,Rt△ABC中,CA=CB,∠ACB=90°,经过顶点B,C作⊙O,分别交边AB,AC于点D,E,连接DE,DC.
(1)求证:AD=ED.
(2)当AE=4,CE=2时,求⊙O的半径.
(3)设=x,tan∠DCB=y.
①求y关于x的函数表达式;
②如图②,连接OE,OD,若=,求y的值.
【解答】(1)证明:∵∠ACB=90°,且⊙O经过B、C、E,
∴直线BE为⊙O的直径,
∴∠BDE=90°,
∴∠CBD+∠CED=180°,
∵∠AED+∠CED=180°,
∴∠AED=∠CBD,
∵CA=CB,
∴∠CAD=∠CBA,
∴∠DEA=∠DAE,
∴AD=ED.
(2)解:∵∠EDA=∠ACB=90°,∠DAE=∠CBA=45°,
∴△ADE∽△CAB,
∴AE=4,AD=DE,
∴AD=DE==2,CA=AE+CE=2+4=6,且,
即,
∴AB=6,
∴DB=AB﹣AD=4,
∴BE===2,
∴⊙O的半径为.
(3)①∵tan∠DCB=y,
∴,,
∴sin∠DCB= sin∠CBD=,cos∠BCD=,
∴tan∠DCB===y,
设EC=m,
∴AE=mx,
∴BC=m+mx=m(1+x),BD=BC﹣AD,AD=AE,
∴BD=m(1+x)﹣mx=m(1+),
∴∠CED=45°,
∴cos∠CED=﹣=,
∴CD2=m2+m2x2+m2x,
∴y===,
②设CE=n,AE=nx,
∴DE=,AC=n(1+x)=BC,
∴S△ABC=AC BC=n2(1+x)2,BE===n,
∴OE=BE=且△OED为等腰三角形,
∴O点到DE的距离为:==n,
∴S△OED=×nx n=n2,
∵=,
∴=,
∵x>0,
∴x=3,
∴y==.
2.已知AB、CD为⊙O的两条弦,AB∥CD.
(1)如图1,求证弧AC=弧BD;
(2)如图2,连接AC、BC、OA、BD,弦BC与半径OA交于点G,延长AO交CD于点E,连接BE,使BE=BD,若OA⊥BC,求证:四边形ABEC为菱形;
(3)在(2)的条件下,CH与⊙O相切于点C,连接CO并延长交BE于点F,延长BE交CH于点H,OF=11,sin∠BDC=,求CH长.
【解答】(1)证明:连接BC,
∵AB∥CD,
∴∠ABC=∠BCD,
∴=;
(2)证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵四边形ABDC是圆的内接四边形,
∴∠BAC+∠BDC=180°,
∴∠ACD=∠BDC,
∵=,
∴AC=BD,
∵BE=BD,
∴AC=BE,∠BED=∠BDC,
∴∠BED=∠ACD,
∴AC∥BE,
∴四边形ABEC是平行四边形,
∵OA⊥BC,
∴平行四边形ABEC是菱形;
(3)解:如图3,延长CF交⊙O于点N,连接BN,
∵CN是直径,
∴∠CBN=90°,
∵AE⊥BC,
∴AE∥BN,
∴∠AOC=∠BNC,
∵∠BDC=∠BNC,
∴∠AOC=∠BDC,
∵sin∠BDC=,
∴sin∠AOC==,
设CO=25x,CG=24x,
∴GO===7x,
∵∠ACD=∠BDC,
∴∠ACD=∠AOC,
又∵∠CAE=∠CAO,
∴△ACO∽△AEC,
∴∠AEC=∠OCA,
∵四边形ABEC是菱形,
∴AC=CE,AE⊥BC,AG=GE,
∴∠CAE=∠CEA,
∴∠CAE=∠ACO,
∴AO=CO=25x,
∴AG=18x=GE,
∴OE=11x,
∵AC∥EB,
∴,
∴=,
∴x=1,
∴CO=25,AG=18,CG=24,
∴CF=36,
∵AC∥BE,
∴∠ACF=∠CFE,
∴∠CFE=∠CAO,
∵CH与⊙O相切于点C,
∴CH⊥CF,
∴∠FCH=90°=∠AGC,
∴△AGC∽△FCH,
∴,
∴=,
∴CH=48.
3.如图,以Rt△BCE的直角边BC为直径作⊙O,交斜边EC于点A,AD⊥BC于点D,点F是BE的中点,连接CF与AD相交于点G,延长AF与CB的延长线相交于点P.
(1)求证:PA是⊙O的切线;
(2)求证:点G为AD的中点;
(3)若2FG=EB,且⊙O的半径长为3,求BD的长度.
【解答】解:(1)证明:如图,连接AO,AB,
∵BC是⊙O的直径,
∴∠BAC=90°,
在Rt△BAE中,F是斜边BE的中点,
∴AF=FB=EF,
∴∠FBA=∠FAB,
又∵OA=OB,
∴∠ABO=∠BAO,
∵∠EBO=90°,
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA是⊙O的切线;
(2)证明:∵BC是⊙O的直径,∠EBO=90°,,
∴EB⊥BC.BE是⊙O的切线
又∵AD⊥BC,
∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC,
∴,,
∴,
∵F是斜边BE的中点,
∴BF=EF,
∴DG=AG,
∴点G为AD的中点;
(3)解:过点F作FH⊥AD于点H,如图,
∵BD⊥AD,FH⊥AD,
∴FH∥BC.
由(2)知,∠FBA=∠BAF,
∴BF=AF.
由已知,有2FG=EB,点F是BE的中点,
∴BF=FG,
∴AF=FG,即△AFG是等腰三角形.
∵FH⊥AD,
∴AH=GH,
∵DG=AG,
∴DG=2HG,
即,
∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,BD=FH,
∵FH∥BC,
∴△HFG∽△DCG,
∴,
∵⊙O的半径长为3,
∴BC=6.
∴,
解得BD=2.
∴BD=2.
4.如图1,AB为⊙O的直径,P为AB延长线上的点,PD为⊙O的切线,切点为D,CD⊥AB,垂足为E,C在⊙O上,连接CO,PC.
(1)求证:PC为⊙O的切线;
(2)如图2,M是线段PC上一点,若OM平分∠COP,OM与线段CE交于点N.
①求证:△OMP∽△ONC;
②若CM=10,tan∠CMO=2,求ON的长.
【解答】证明:(1)连接OD,如图1,
∵PD为⊙O切线,
∴∠ODP=90°,
∵AB⊥CD,且AB为⊙O直径,
∴AB垂直平分CD,
∴PC=PD,
∴∠PCD=∠PDC,
又∵OC=OD,
∴∠OCD=∠ODC,
∴∠OCP=∠OCD+∠PCD=∠ODC+∠PDC=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)①∵AB⊥CD,
∴∠CEP=90°,
∴∠ECP+∠MPO=90°,
又∠OCD+∠ECP=90°,
∴∠MPO=∠OCD,
又OM平分∠COP,
∴∠CON=∠MOP,
∴△OMP∽△ONC;
(2)②∵∠CNM=∠CON+∠OCN,
∠CMO=∠CPO+∠MOP,
∴∠CNM=∠CMN,
∴CM=CN=10,
过点C作CG⊥MN于G,
∵tan∠CMO=2,
∴NG=MG=2,CG=4,
在Rt△OCM中,由勾股定理得:OM=,
∴ON=OM﹣MN=10.
5.如图,AB是⊙O的直径,C、D是⊙O上两点.AE与过点C的切线垂直,垂足为E,直线EC与直径AB的延长线相交于点P,弦CD交AB于点F,连接AC、AD、BC、BD.
(1)若∠ABC=∠ABD=60°,判断△ACD的形状,并证明你的结论;
(2)若CD平分∠ACB,求证:PC=PF;
(3)在(2)的条件下,若AD=5,PF=5,求由线段PC、和线段BP所围成的图形(阴影部分)的面积.
【解答】解:(1)△ACD是等边三角形,
理由如下:
=,
∴∠ACD=∠ABD=60°,
∵=,
∴∠ADC=∠ABC=60°,
∴△ACD是等边三角形;
(2)如图1,
连接OC,OD,
∵PC切⊙O于C,
∴OC⊥PC,
∴∠PCO=90°,
∴∠OCF+∠PCF=90°,
∵CD平分∠ACB,
∴=,
∴∠DOB=∠AOD=90°,
∴∠ODF+∠OFD=90°,
∵OC=OD,
∴∠ODF=∠OCF,
∴∠PCF=∠OFD,
又∵∠CFP=∠OFD,
∴∠PFC=∠CFP,
∴PC=PF;
(3)由(2)知,
=,
∴AD=BD=5,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AB==10,
∴OC=5,
∵PC=PF,
∴PC=5,
∵tan∠BOC==
∴∠BOC=60°,
∵S△PCO=OC PC==,
S扇形BOC==,
∴S阴影=S△PCO﹣S扇形BOC=﹣.
6.已知四边形ABCD内接于⊙O,AB=AD.
(1)如图1,求证:点A到∠C两边的距离相等;
(2)如图2,已知BD与AC相交于点E,BD为⊙O的直径.①求证:tan∠CAD=;②若∠CBD=30°,AD=,求AE的长.
【解答】证明:(1)如图1,连接AC,
∵AB=AD,
∴,
∴∠ACB=∠ACD,
∴点A到∠C两边的距离相等;
(2)①∵,
∴∠CAD=∠CBD,
∵BD为直径,
∴∠BCD=90°,
∴tan∠CAD=tan∠CBD=,
如图2,过点D作DQ∥EC,交BC延长线于点Q,
∴∠ACB=∠Q,∠ACD=∠CDQ,
又由(1)知:∠ACB=∠ACD,
∴∠CDQ=∠Q,
∴CD=CQ,
∵CE∥DQ,
∴
∴,
∴tan∠CAD=,
②如图,
由(2)①得:∠CAD=∠CBD=30°,
则tan∠CAD==,
设DE=a,则BE=a,
∵BD为直径,
∴∠BAD=90°,
∵AB=AD=3,
∴BD=6,
∴a+a=6,
解得:a=3,
∴DE=3﹣3,BE=9﹣3,
又∵∠BCD=90°,
∴CD=BD sin∠CBD=3,
∵∠BDC=∠BAC,∠ABD=∠ACD,
∴△BAE∽△CDE,
∴,
∴AE=(3﹣3)×=3﹣3.
7.如图,⊙O的内接四边形ABCD的两条对角线相交于点E,两组对边的延长线分别相交于点F,G,且∠F=67.5°,∠G=22.5°,=,边AB过圆心O.
(1)求∠BAD的度数;
(2)求∠BAC的正切值;
(3)若AB=2,则CE CA的值等于多少?
【解答】解:(1)如图,∵AB经过圆心O,
∴AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵∠F=67.5°,
∴∠DAC=∠ACB﹣∠F=90°﹣67.5°=22.5°,
∵,
∴∠DAC=∠BAC=22.5°,
∴∠BAD=22.5°+22.5°=45°.
(2)如图,设⊙O的半径为r,连接OD,则OD=OA=OB=r,
∴∠ODA=∠OAD=45°,
∴∠AOD=∠GOD=90°,
∵∠BDC=∠BAC=22.5°,∠G=22.5°,
∴∠BDC=∠BAC=∠BGC,
∴BG=BD==r,
∴tan∠BAC=tan∠BGC===.
(3)如图,∵∠ACB=90°,tan∠BAC=,
∴=tan∠BAC=,
∴AC=()BC,
由AC2+BC2=AB2,且AB=2,得()2BC2+BC2=22,
解得,BC2=;
∵,
∴∠CBE=∠CAB,
∵∠BCE=∠ACB,
∴△BCE∽△ACB,
∴,
∴CE CA=BC2=.
8.如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
(1)求证:PE是⊙O的切线;
(2)试判断△AEF的形状,并说明理由;
(3)若AF=2,AE=,求OA的长.
【解答】(1)证明:连接OE,
∴∠AOE=2∠ACE,
∵∠B=2∠ACE,
∴∠AOE=∠B,
∵∠P=∠BAC,
∴∠ACB=∠OEP,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OEP=90°,
∴PE是⊙O的切线;
(2)解:△AEF是等腰三角形,理由如下:
∵OA=OE,
∴∠OAE=∠OEA.
∵∠AFE=∠AOE+∠EFO,∠AOE=∠B,∠B=∠AEF,
∴∠AOE=∠AEF.
∴∠AFE=∠AEF+∠FEO=∠OEA.
∴∠OAE=∠AFE.
∴△AEF是等腰三角形;
(3)∵OA=OE,
∴∠OAE=∠OEA,
∵AE=EF,
∴∠EAF=∠AFE,
∴∠OAE=∠OEA=∠EAF=∠AFE,
∴△AEF∽△AOE,
∴=,
∵AF=2,AE=EF=,
∴OA=5.
9.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积;
(4)在(3)的条件下,求的长度.
【解答】解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵,,
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°﹣∠BPM=180°﹣(∠APC+∠BPC)=180°﹣120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PCB=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
在△ACM和△BCP中,
,
∴△ACM≌△BCP(AAS);
(3)∵CM∥BP,
∴四边形PBCM为梯形,
作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP,AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+AMB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=,
∴S四边形PBCM=(PB+CM)×PH=(2+3)×=;
(4)过点B作BQ⊥AP,交AP的延长线于点Q,过点A作AN⊥BC于点N,连接OB,
∵∠APC=∠BPC=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴PQ=PB=1,
在Rt△BPQ中,BQ=,
在Rt△AQB中,AB=,
∵△ABC为等边三角形,
∴AN经过圆心O,
∴BN=AB=,
∴AN=,
在Rt△BON中,设BO=x,则ON=,
∴,
解得:x=,
∵∠BOA=∠BCA=120°,
∴的长度为.
10.如图,点B是⊙C上的一点,点A是直径ED延长线上的一点,连接AB,EB,BD,且∠ABD=∠E.
(1)求证:直线AB是⊙C的切线;
(2)当时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=4,求⊙C的半径.
【解答】证明:(1)连接CB,如图,
∵ED为圆的直径,
∴∠DBE=90°.
∴∠CBD+∠CBE=90°.
∵CB=CE,
∴∠CBE=∠CEB,
∴∠CBD+∠CEB=90°.
∵∠ABD=∠E,
∴∠CBD+∠ABD=90°,
即∠ABC=90°,
∴AB⊥BC.
∴直线AB是⊙C的切线;
(2)过点D作DH⊥AB于点H,如图,
则DH∥BC.
∵,
∴设AB=4x,则BC=3x.
∵AB⊥BC,
∴AC==5x,
∵CD=CB=3x,
∴AD=AC﹣CD=2x.
∵DH∥BC,
∴=.
∴,.
∴DH=x,AH=x.
∴BH=AB﹣AH=x,
在Rt△BHD中,tan∠HBD=.
∵∠ABD=∠E,
∴tanE=tan∠HBD=.
(3)过点F作FM⊥CE于M,如图,
∵tanE=,
∴.
由(2)知:AB=4x,BC=3x,AC=5x,AD=2x,
∵CE=CB=3x,
∴AE=AD+CD+CE=8x.
∵AF是∠BAC的平分线,
∴.
∴FE=BE.
在Rt△BDE中,tanE==,
则BE=2BD.
∵BD2+BE2=DE2,
∴BD2+(2BD)2=(6x)2.
∴BD=,
∴BE=2BD=x.
∴FE=x.
在Rt△BDE中,tanE==,则ME=2MF.
∵FM2+ME2=FE2,
∴.
∴FM=x.
∴ME=2FM=x,
∴AM=AE﹣ME=(8﹣)x=x.
在Rt△AFM中,
∵AM2+FM2=AF2,
∴.
解得:x=±(负数不合题意,舍去).
∴x=.
∴⊙C的半径CE=3x=.
11.如图1,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交BC于E,连接AE交CD于G,交⊙O于F,连接DF,∠BAC=∠EFD.
(1)求证:AB与⊙O相切;
(2)如图2,若AF:FG=3:2,
①若AF=6,求线段CG的长;
②求tan∠CAE的值.
【解答】证明:(1)∵∠BCD=∠DFE,∠BAC=∠EFD,
∴∠BCD=∠BAC.
∵∠ACB=90°,
∴∠BAC+∠B=90°,
∴∠BCD+∠B=90°.
即∠CDB=90°,
∴CD⊥AB.
∴AB与⊙O相切;
解:(2)①连接CF,如图,
∵AF:FG=3:2,AF=6,
∴FG=4.
∴AG=AF+FG=10.
∵CD为⊙O的直径,
∴∠CFD=90°,
∴∠FCD+∠FDC=90°.
∵∠CEF=∠FDC,
∴∠FCD+∠FEC=90°.
∵∠ACB=90°,
∴∠CAE+∠CEF=90°.
∴∠FCD=∠CAE.
∵∠CGF=∠AGC,
∴△CGF∽△AGC.
∴.
∴CG2=AG GF=4×10=40.
∴CG=2.
②过点F作FH⊥CD于点H,如图,
∵FH⊥CD,AD⊥CD,
∴FH∥AD.
∴.
设DH=3x,则GH=2x,
∴CH=HG+CG=2+2x.
∵∠CFD=90°,FH⊥CD,
∴△FHD∽CHF.
∴.
∴FH2=HD CH=3x(2+2x).
在Rt△FGH中,
∵FH2+CH2=FG2,
∴3x(2+2x)+(2x)2=42.
解得:x=或x=﹣(不合题意,舍去).
∴GH=,FH=,
∴CH=CG+GH=.
在Rt△FCH中,tan∠FCH=.
∵∠FCH=∠CAE,
∴tan∠CAE=tan∠FCH=.
12.如图,AB、CD都是⊙O的直径,连接AD,BC.
(1)求证:AD=BC;
(2)过D点作⊙O的切线DE交BA的延长线于点E,F是BE上一点,连接CF交⊙O于点M,若ED=CF,求证:∠BED=∠CFB.
(3)在(2)的条件下,连接DM交EB于点N,连接CN,若tan∠CNO=,ON=2,求DE的长.
【解答】(1)证明:∵在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴AD=BC;
(2)证明:如图2,过点C作CG⊥AB于G,过点D作DH⊥AB于H,
在△ODH和△OCG中,
,
∴△ODH≌△OCG(AAS),
∴DH=CG,
在Rt△EDH和Rt△FCG中,
,
∴Rt△EDH≌Rt△FCG(HL),
∴∠BED=∠CFB;
(3)解:如图3,过点C作CG⊥AB于G,过点D作DH⊥AB于H,
∵CD是⊙O的直径,
∴∠CMD=90°,
∴∠FMN=90°,
∴∠MFN+∠FNM=90°,
∵ED是⊙O的切线,
∴∠ODE=90°,
∴∠NOD+∠E=90°,
∵∠BED=∠CFB,∠FNM=∠DNO,
∴∠DNO=∠NOD,
∴DN=DO,
∵DH⊥AB,ON=2,
∴NH=HO=,
由(2)可知:△ODH≌△OCG,
∴OG=OH=,
∴NG=3,
∵tan∠CNO==,
∴CG=2,
由勾股定理得:OC===5,
∵∠EDO=∠CGO=90°,∠EOD=∠COG,
∴△EOD∽△COG,
∴=,即=,
解得:ED=10.
13.如图,AB是⊙O的直径,点C在⊙O上,且AB=2,=,D是⊙O上一动点,连接BD,过点B作BE⊥BD交直线DC于点E.
(1)当点D是的中点时,求△BCD的面积;
(2)过点B作BF⊥DE于点F,求的值;
(3)在点D运动过程中,求线段AE的最大值.
【解答】解:(1)过点D作DH⊥BC交BC的延长线于点H,连接OD交AC于点M,
∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AC,
设AC=x,则BC=2x,
在Rt△ACB中,AC2+BC2=AB2,
∴(x)2+(2x)2=(2)2,
解得x=2或﹣2(舍去),
∴AC=2,BC=4,
∵点D是的中点,
∴OD⊥AC,AM=CM,
∴四边形CHDM是矩形,
∴DH=CM=AC=,
∴S△BCD=×DH×BC=××4=2;
(2)在Rt△ACB中,cos∠CAB===,
∵∠EDB=∠CAB,
∴cos∠EDB=∠cosCAB=,
在Rt△BFD中,cos∠FDB=,
∴DF=BD,
在Rt△BED中,cos∠EDB=,
∴BD=DE,
∴DF=DE,
∴=;
(3)当点D与点A重合时,AE的值最大,此时BD与AB重合,
由(2)知,BD=DE,且BD=AB=2,
∴AE=DE=.
14.如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=,求⊙O的半径.
【解答】(1)证明:连接OB,
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC,
又∵CD⊥OA,
∴∠A+∠AED=∠A+∠CEB=90°,
∴∠OBA+∠ABC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:如图1,连接OF,AF,BF,
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°,
∴∠ABF=∠AOF=30°;
(3)解:连接OF,如图2所示:
∵DA=DO,CD⊥OA,
∴AF=OF=OA,
过点O作OG⊥AB于点G,则AG=BG,
在Rt△AOG中,sin∠BAO===,
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,
∴AB=10+13x,
则AG=AB=5+x,
又∵Rt△AOG中,sin∠BAO=,则=,
则=,
解得x=,
∴AO=24x=.
15.如图,在Rt△ABC中,∠C=90°,O为AB上一点,以点O为圆心,OA为半径作⊙O,分别交AB、AC于点E、F,且与BC相切于点D,连接OF.解答下列问题:
(1)∠BAC与∠OFA之间的关系是 相等 ;
(2)求证:∠AFO=2∠BAD;
(3)若=,求tan的值.
【解答】解:(1)∵OA=OF,
∴∠OAF=∠OFA,
即∠BAC=∠OFA,
故答案为:相等;
(2)证明:连接OD,如图,
∵BC为切线,
∴OD⊥BC,
∵∠C=90°,
∴OD∥AC,
∴∠ODA=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,
∴∠OAC=2∠OAD,
∵OA=OF,
∴∠OAC=∠AFO,
∴∠AFO=2∠BAD;
(3)作OH⊥AF于H,如图,则AH=HF,
∵=,
∴设AH=HF=2x,则CF=3x,
∵∠ODC=∠C=∠OHC=90°,
∴四边形ODCH为矩形,
∴OH=CD,OD=CH=2x+3x=5x,
在Rt△AOH中,OH==x,
∴CD=x,
在Rt△ACD中,tan∠CAD===.
∴tan的值为.
16.如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=3,EF=5,
①求证:DE=EF;
②求⊙O的半径.
【解答】(1)证明:如图(1),连接BD,
∵∠BAD=90°,
∴BD是⊙O的直径,
∴∠BCD=∠DCE=90°,
∴∠DEC+∠CDE=90°,
∵∠BAC=∠BDC,∠BAC=∠DEC,
∴∠BDC+∠CDE=90°,即∠BDE=90°,
∴DE是⊙O的切线.
(2)①证明:由(1)得:∠BDE=90°,
∴∠ADB+∠EDF=90°,
∵∠BAD=90°,
∴∠ABC+∠F=90°,
∴∠ADB+∠EDF=∠ABC+∠F,
∵AB=AC,
∴∠ADB=∠ABC,
∴∠EDF=∠F,
∴DE=EF.
②解:∵DE=EF,
∴DE=EF=5,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴CD===4,
∠BDC+∠DBC=90°,
又∵∠BDC+∠EDC=90°,
∴∠DBC=∠EDC,
∴△CDE∽△CBD,
∴,
∴,
∴BD=,
∴⊙O的半径为.
17.如图,⊙O是△ABC的外接圆,AB是的直径,D是AB延长线上的一点,连接DC,∠DCB=∠A,CE⊥AB于点E.
(1)求证DC是⊙O的切线;
(2)若AC=4,tan∠BCE=,求DC的长;
(3)在(2)的条件下,若M是线段AC上一动点,求OM+AM的最小值.
【解答】(1)证明:如图,
根据题意连接OC,则有OC=OA,
∴∠A=∠OCA=∠BCD,
∵AB是圆的直径,
∴∠ACB=90°,即∠OCA+∠OCB=90°,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴OC⊥CD,
∴DC是⊙O的切线.
(2)由(1)可知∠A+∠ABC=90°,∠ECB+∠ABC=90°,
∴∠A=∠ECB,
∴Rt△ABC~Rt△CBE,
∴=,
∵AC=4,tan∠BCE=,
∴==,解得BC=2,
∴AB==2,
∴OC=OB=,
∵=,即,解得BE=,
∴CE=,
∵Rt△DCE与Rt△DOC有公共角∠D,
∴Rt△DCE~Rt△DOC,
∴=,即DC2=DO DE=(+BD)(+BD),
在Rt△DOC中有:DC2+OC2=OD2,
即(+BD)(+BD)+=(+BD)2,
解得BD=,
∴DC==.
(3)如图,作点O关于AC的对称点O′,连接AO′,CO′,OC,O′M,过点M作MH⊥AO于H.过点O′作O′P⊥AB于P.
∵tan∠MAH==,
∴MH=AM,
∵MO=MO′,
∴OM+AM=O′M+MH≤O′P,
∴当M,H在O′P上时,OM+AM的值最小,最小值为线段O′P的长,
∵OA=OC=AO′=CO′,
∴四边形AOCO′是菱形,
∴S菱形AOCO′= AC OO′=AO PO′,
∴PO′==,
故OM+AM的最小值为.
18.如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若tan∠ADC=,AC=2,求⊙O的半径;
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.
【解答】解:(1)CD与⊙O相切,理由:
如图1,连接OD,
∵OB=OD,
∴∠ODB=∠CBD,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB为⊙O的直径,
∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDA+∠ADO=90°,
∴∠CDO=90°,
∴OD⊥CD,
∴CD与⊙O相切;
(2)由(1)知,∠CBD=∠ADC,
∵tan∠ADC=,
∴tan∠CBD=,
在Rt△ADB中,tan∠CBD==,
∵∠C=∠C,∠ADC=∠CBD,
∴△CAD∽△CDB,
∴,
∴CD=2CA=4,
∴CB=2CD=8,
∴AB=CB﹣CA=8﹣2=6,
∴OA=OB=AB=3;
(3)如图2,连接OE,过点E作EG⊥BD于G,
∵DE平分∠ADB,
∴∠ADE=∠BDE=45°,
∴∠BOE=2∠BDE=90°,
∴BE==3,
在Rt△ABD中,AD2+BD2=AB2=62,
∵,
∴AD=,BD=,
∵EG⊥BD,∠BDE=45°,
∴∠DEG=∠BDE=45°,
∴DG=EG,
设DG=EG=x,则BG=BD﹣DG=﹣x,
在Rt△BEG中,EG2+BG2=BE2=(3)2=18,
∴x2+(﹣x)2=18,
∴x=或x=(舍),
∴EG=,
∴sin∠DBE==.
19.如图1,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.
(1)求证:△ADG∽△CFG.
(2)若G是的中点,当CG与△ADE的一边平行时,求的值.
(3)如图2,点E是OB的中点,AB=8,连接BG,BD,BC.当DG+CG=6时,求cosF的值.
【解答】解:(1)∵四边形AGCD为⊙O的内接四边形,
∴∠AGC+∠ADC=180°,∠DAG+∠DCG=180°,
∵∠AGC+∠CGF=180°,∠DCG+∠GCF=180°,
∴∠CGF=∠ADC,∠DAG=∠GCF,
∴△ADG∽△CFG;
(2)①当CG∥AD时,
∵G是的中点,
∴
∴AG=CG,
则△ADG≌△CFG(AAS),
∴∠ADG=∠F,∠DAG=∠DAG,
∴△DAG∽△AFD,
∴,
设CF=x,AG=y,
∴,
解得x=y,
∴;
②当CD∥AE时,
∴∠GCF=90°
∵∠DOB=∠AOG,
∴,
∴,
∴∠AOG=60°,
∴∠GDA=∠F=30°,
∴=tanF=tan30°=;
(3)延长CD至点M,使DM=CG,连BM,过B作BN⊥MG,连OD,
∵MD=CG,∠MDB=∠BCG,BD=BC,
∴△MDB≌△GCB(SAS),
∴BM=GB,
∵E为OB中点,CD⊥AB,
∴OD=BD=OB,
∴△BDO为等边三角形,
∴∠DOB=60°,
∴∠DGB=30°,
∴GM=DG+DM=DG+GC=6,
∴GN=GM=3,GB=6,
由(1)得,∠F=∠ADG=∠ABG,
在Rt△ABG中,cosF=cos∠ABG=.
20.如图,四边形BCDE是⊙O的内接四边形,DE是⊙O的直径,BC、ED的延长线交于点A,连接CE、BD交于点F,DF2=FC FE,点H是线段CE上一点连接BH、DH.
(1)求证:DF=BF;
(2)若∠BEC=∠DBH,∠BDE=45°,求;
(3)在(2)的条件下,若AE=AC,CB+DE=2+2.求线段AC的长度.
【解答】(1)证明:∵∠BCE=∠EDB,∠CBD=∠DEC,
∴△BCF∽△EDF,
∴=,
∴DF BF=FC FE,
∵DF2=FC FE,
∴DF2=DF BF,
∴DF=BF;
(2)解:∵∠BEC=∠BDC,∠BEC=∠DBH,
∴∠BEC=∠BDC=∠DBH,
∴CD∥BH,
∴△CFD∽△HFB,
∴=,
∵DF=BF,
∴CF=HF,
∴四边形CDHB是平行四边形,
∴BC∥DH,
∴∠DHC=∠BCE=∠BDE=45°,∠BHC=∠DCE=90°,
∴△DHC、△BHC是等腰直角三角形,
∴=,
∵CF=HF,
∴CH=2CF,
∴=2;
(3)解:∵四边形CDHB是平行四边形,
∴HD∥BC,HD=BC,CD∥BH,CD=BH,
∴=,
∴,
∵AE=AC,
∴DE=DH,
∵CB+DE=2+2.
∵HD=BC,
∴DH+DH=2+2.
解得:DH=2,
∴DE=2.
∵△DHC、△BHC是等腰直角三角形,
∴CD=CH=BH=,BE=,
∵∠CHB=90°,
∴∠EHB=90°,
∴EH==2,
∴CE=CH+EH=3,
∵四边形BCDE是⊙O的内接四边形,
∴∠CDE+∠EBC=180°,
∵∠CDE+∠ADC=180°,
∴∠ADC=∠EBC,
∵∠DCE=90°,∠BCE=45°,
∴∠ACD=∠ECB=45°,
∴△ACD∽△ECB,
∴,即=,
∴AC=3.
21.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,连接OA、OB、OC,延长BO与AC交于点D,与⊙O交于点F,延长BA到点G,使得∠BGF=∠GBC,连接FG.
(1)求证:FG是⊙O的切线;
(2)若⊙O的半径为3.
①当OD=2,求AD的长度;
②当△OCD是直角三角形时,求△ABC的面积.
【解答】(1)证明:连接AF,
∵BF为⊙O的直径,
∴∠BAF=90°,∠FAG=90°,
∴∠BGF+∠AFG=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠AFB,∠BGF=∠ABC,
∴∠BGF=∠AFB,
∴∠AFB+∠AFG=90°,即∠OFG=90°,
∴OF⊥FG,
又∵OF为半径,
∴FG是⊙O的切线;
(2)解:①连接CF,则∠ACF=∠ABF,
∵AB=AC,AO=AO,BO=CO,
∴△ABO≌△ACO(SSS),
∴∠ABO=∠BAO=∠CAO=∠ACO,
∴∠CAO=∠ACF,
∴AO∥CF,
∴=,
∵半径是3,OD=2,
∴DF=OF﹣OD=1,BD=OB+OD=5,
∴==2,即CD=AD,
∵∠ABD=∠FCD,∠ADB=∠FDC,
∴△ADB∽△FDC,
∴=,
∴AD CD=BD DF,
∴AD CD=5,即AD2=5,
∴AD=(负值舍去);
②∵△ODC为直角三角形,∠DCO不可能等于90°,
∴存在∠ODC=90°或∠COD=90°,
当∠ODC=90°时,
由①知∠ACO=∠ACF,
∴OD=DF=,BD=,
∵OD⊥AC,
∴AD=CD,
由①可知AD CD=BD DF,
∴AD CD=AD2=×=,
∴AD=,
∴AC=2AD=3,
∴S△ABC=×AC×BD=×3×=;
当∠COD=90°时,
∵OB=OC=3,
∴△OBC是等腰直角三角形,
∴BC=3,
延长AO交BC于点M,则AM⊥BC,
∴MO=,
∴AM=3+,
∴S△ABC=×BC×AM=×3×(3+)=,
∴△ABC的面积为或.
22.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切:
(2)若,求的值;
(3)在(2)的条件下,若⊙O的半径为4,PD=OD,求EC的长.
【解答】(1)证明:如图,连接OB,则OB=OD,
∴∠BDC=∠DBO,
∵∠BAC=∠BDC、∠BDC=∠GBC,
∴∠GBC=∠BDC,
∵CD是⊙O的直径,
∴∠DBO+∠OBC=90°,
∴∠GBC+∠OBC=90°,
∴∠GBO=90°,
∴PG与⊙O相切;
(2)解:过点O作OM⊥AC于点M,连接OA,
则∠AOM=∠COM=∠AOC,
∵=,
∴∠ABC=∠AOC,
又∵∠EFB=∠OMA=90°,
∴△BEF∽△OAM,
∴=,
∵AM=AC,OA=OC,
∴=,
又∵=,
∴=2×=2×=2×=;
(3)解:∵PD=OD,∠PBO=90°,
∴BD=OD=4,
在Rt△DBC中,BC===4,
又∵OD=OB,
∴△DOB是等边三角形,
∴∠DOB=60°,
∵∠DOB=∠OBC+∠OCB,OB=OC,
∴∠OCB=30°,
∴=,=,
∴可设EF=x,则EC=2x、FC=x,
∴BF=4﹣x,
∵=,且OC=4,
∴BE=5,
在Rt△BEF中,BE2=EF2+BF2,
∴100=x2+(4﹣x)2,
解得:x=6±,
∵>4,舍去,
∴x=,
∴EC=6﹣,
∴OE=4﹣(6﹣)=﹣2.
23.如图,在△ABC中,∠A=90°,D是边AC上一动点,且不与A,C两点重合,连接BD,过点D作DE⊥BD交边BC于点E,△BDE的外接圆交边AB于另一点F,连接DF.
(1)求证:△ADF∽△DBE.
(2)当AB=6,AC=8时.
①若AD=3AF,求AD的长.
②当线段DE,DF,BF中有两条相等时,求出所有符合条件的tan∠ADF的值.
(3)若BD平分∠ABC,S△ADF=1,S△BDE=6,则S△CDE= .
【解答】解:(1)证明:∵四边形FBED为圆内接四边形,
∴∠DFA=∠DEB,
∵DE⊥BD,
∴∠EDB=∠A=90°,
∴△ADF∽△DBE;
(2)连接EF,
①设AF=t,AD=3t,
则BF=6﹣t,BD=,
∵∠EDB=90°,
∴EB为直径,
∴∠EFB=∠A=90°,
∵∠EBF=∠CBA,
∴△EFB∽△CAB,
∴=,
∴BE=(6﹣t),
∵△ADF∽△DBE,
∴=,
∴=,
整理得,13t2+60t﹣108=0,
解得,t=或t=﹣6(舍去),
∴AD=3t=.
②设AF=t,tan∠ADF=m,
则AD=,DB=,BE=(6﹣t),
1°.当BF=DF=6﹣t时,
∵△ADF∽△DBE;
∴=,
∴=,
解得m=t,
∴AD=,
在Rt△ADF中,由勾股定理得,
AF2+AD2=FD2,
即t2+()2=(6﹣t)2,
解得t=,
∴tan∠ADF=m=t=;
2°.当DF=DE=时,
∵△ADF∽△DBE;
∴=,
∴=,
=10t﹣t2①,
在Rt△BDE中,由勾股定理得,
BD2+DE2=BE2,
即36+++t2=[(6﹣t)]2②,
将①代入②得,
36+10t﹣t2+10t﹣t2+t2=[(6﹣t)]2,
整理得,2t2﹣15t+18=0
解得t=6(舍去)或t=,
将t=代入①得,
m2=,
∴m=;
3°.当BF=DE=6﹣t时,
∵BE=BE,
∴Rt△EFB≌Rt△BDE(HL),
∴∠DBE=∠FEB,
∵△ADF∽△DBE,
∴∠ADF=∠DBE,
∴∠ADF=∠FEB,
∵∠EFB=∠A=90°
∴EF∥AC,
∴∠FEB=∠ACB,
∴∠ADF=∠ACB,
∴tan∠ADF=tan∠ACB==,
综上所有符合条件的tan∠ADF的值为:或或;
(3)设AF=t,
∵S△ADF=AF AD=1,
∴AD=,
∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ADF,
∴△ADF∽△ABD,
∴=,
∴AB=,
∴BF=﹣t,
∵△ADF∽△DBE,
∴=()2=()2=,
∴BD=AD=,
BE=DF=×,
在Rt△ABD中,由勾股定理得,
AD2+AB2=BD2,
即()2+()2=()2,
t4=,
∵△EFB∽△CAB,
∴=,
∴BC====4××=×,
∴AC2=BC2﹣AB2=(×)2﹣()2=(t2+)﹣=×(+4×)﹣16×()3=,
AB2=()2=16×()3=10,
∴AC2 AB2=10×=625,
∴S△ABC=AB AC=,
∵△ADF∽△ABD,
∴=()2==,
∴S△ADB=5S△ADF=5,
∴S△CDE=S△ABC﹣S△ADB﹣S△BDE=﹣5﹣6=.
24.如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
【解答】(1)证明:如图1中,连接BC.
∵=,
∴∠DCB=∠DBC,
∵AB是直径,
∴∠ACB=∠BCE=90°,
∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,
∴CD=ED.
(2)①证明:如图2中,
∵CF=CH,
∴∠CFH=∠CHF,
∵∠AFO=∠CFH,
∴∠AFO=∠CHF,
∵=,
∴∠CAD=∠BAD,
∴△AFO∽△AHC,
∴=,
∴=,
∴CF AF=OF AH.
②解:如图3中,连接OD交BC于G.设OG=x,则DG=2﹣x.
∵=,
∴∠COD=∠BOD,
∵OC=OB,
∴OD⊥BC,CG=BG,
在Rt△OCG和Rt△BGD中,则有22﹣x2=12﹣(2﹣x)2,
∴x=,即OG=,
∵OA=OB,
∴OG是△ABC的中位线,
∴OG=AC,
∴AC=.
25.如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为,△ABC的面积为2,求CD的长;
(3)在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若=,求BF的长.
【解答】(1)证明:连接OC,如图:
∵AB为⊙O的直径,
∴∠ACB=90°,∠A+∠ABC=90°,
∵OB=OC,
∴∠ABC=∠BCO,
又∠BCD=∠A,
∴∠BCD+∠BCO=90°,即∠DCO=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)过C作CM⊥AB于M,过B作BN⊥CD于N,如图:
∵⊙O的半径为,
∴AB=2,
∵△ABC的面积为2,
∴AB CM=2,即×2 CM=2,
∴CM=2,
Rt△BCM中,∠BCM=90°﹣∠CBA,
Rt△ABC中,∠A=90°﹣∠CBA,
∴∠BCM=∠A,
∴tan∠BCM=tanA,即=,
∴=,
解得BM=﹣1,(BM=+1已舍去),
∵∠BCD=∠A,∠BCM=∠A,
∴∠BCD=∠BCM,
而∠BMC=∠BNC=90°,BC=BC,
∴△BCM≌△BCN(AAS),
∴CN=CM=2,BN=BM=﹣1,
∵∠DNB=∠DMC=90°,∠D=∠D,
∴△DBN∽△DCM,
∴==,
即==,
解得DN=2﹣2,
∴CD=DN+CN=2;
方法二:过C作CM⊥AB于M,连接OC,如图:
∵⊙O的半径为,
∴AB=2,
∵△ABC的面积为2,
∴AB CM=2,即×2 CM=2,
∴CM=2,
Rt△MOC中,OM==1,
∵∠DMC=∠CMO=90°,∠CDM=90°﹣∠DCM=∠OCM,
∴△DCM∽△COM,
∴=,即=,
∴CD=2;
(3)过C作CM⊥AB于M,过E作EH⊥AB于H,连接OE,如图:
∵CM⊥AB,EH⊥AB,
∴==,
∵=,
∴==,
由(2)知CM=2,BM=﹣1,
∴HE=1,MF=2HF,
Rt△OEH中,OH===2,
∴AH=OA﹣OH=﹣2,
设HF=x,则MF=2x,
由AB=2可得:BM+MF+HF+AH=2,
∴(﹣1)+2x+x+(﹣2)=2,
解得:x=1,
∴HF=1,MF=2,
∴BF=BM+MF=(﹣1)+2=+1.
26.如图1,以△ABC的边AC为直径作⊙O交BC于点D,连接AD,点E为AD上一点(不与端点重合),连接CE,作DF⊥CE于点F,延长DF交AC于点M,交BA的延长线于点G,∠BGD=∠ACE.
(1)求证:BG是⊙O的切线;
(2)求证:;
(3)如图2,延长CE交AB于点H,若HE=4,∠ACH=∠BCH,sin∠BGD=,求BC的长.
【解答】解:(1)∵∠BGD=∠ACE,且∠AMG=∠CMF,
∴180°﹣∠BGD﹣∠AMG=180°﹣∠ACE﹣∠CMF,即∠GAM=∠CFM,
∵DF⊥CE,
∴∠GAM=∠CFM=90°,
∴OA⊥BG,
∴BG是⊙O的切线;
(2)∵AC为⊙O直径,
∴∠ADC=∠ADB=90°,
∵OA⊥BG,
∴∠B=90°﹣∠ACB=∠DAC,
∴△ADB∽△CDA,
∴=,
∴AB AD=AC BD,
∵∠B=∠DAC,∠BGD=∠ACE,
∴△BGD∽△ACE,
∴=,
∴AC BD=BG AE,
∴AB AD=BG AE,
∴;
(3)设CH交⊙O于N,连接AN,如图:
∵AC为⊙O直径,
∴∠ADC=90°=∠ANC,
∵DF⊥CE,
∴∠FCD=90°﹣∠FDC=∠EDF,AN∥DG,
∴∠BGD=∠HAN,∠NAD=∠ADG,
∵∠ACH=∠BCH,∠BGD=∠ACE,
∴∠ACH=∠BCH=∠EDF=∠BGD=∠HAN=∠NAD,
在△AHN和△AEN中,
∴△AHN≌△AEN(ASA),
∴HN=EN=HE,AH=AE,
∵HE=4,
∴HN=EN=2,
∵sin∠BGD=,
∴sin∠HAN=,
Rt△AHN中,=可得AH=5=AE,
Rt△AHC中,sin∠ACH=sin∠BGD=,
∴=,可得CH=,
∴AC==,EC=CH﹣HE=,
∵∠B=∠DAC,∠ACE=∠BCH,
∴△AEC∽△BHC,
∴=,
∴=,
∴BC=.
27.如图,点I是O△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)求证:DG是⊙O的切线;
(2)若DE=4,BE=5,求DI的长;
(3)若sin∠ACD=,CD=10,求△ACD的内心到点O的距离.
【解答】(1)证明:连接OD.
∵点I是△ABC的内心,
∴∠CBD=∠ABD,
∴=,
∴OD⊥AC,DC=DA,
∴∠ODA=∠CDA,
∵DG平分∠ADF,
∴∠ADG=∠ADF,
∴∠ODG=∠ODA+∠ADG=(∠CDA+∠ADF)=90°,
∴OD⊥DG,
∴DG是⊙O的切线.
(2)解:∵点I是△ABC的内心,
∴∠BAI=∠CAI,
∵∠EIA=∠IBA+∠IAB=∠CAD+∠CAI,
即∠DIA=∠DAI,
∴DA=DI,
∵∠DAE=∠DBA,∠ADE=∠BDA,
∴△DAE∽△DBA,
∴AD:DB=DE:DA,
即AD:9=4:AD,
∴AD=6,
∴DI=6.
(3)解:如图,连接OD交AC于T,设G是△ACD的内心,连接CG,OC.
∵DC=DA,OD⊥AC,
∴OD平分∠CDA,
∴△ACD的内心在DT上,
在Rt△CDT中,CD=10,sin∠DCT==,
∴DT=6,
∴CT=AT===8,
设OD=OC=x,
在Rt△OCE中,则有x2=82+(x﹣6)2,
∴x=,
∴OT=﹣6=,
∵G是△ACD的内心,
∴ (CD+AD+AC) GT= AC DT,
∴GT==,
∴OG=OT+GT=+=5.
∴△ACD的内心到点O的距离为5.
28.如图,以Rt△ABC的斜边AC为直径作⊙O,点D在半径OC上,过点D作AC的垂线,分别交弦BC于点E,交⊙O于F.在射线DE上取点G,连接GB并延长交CA的延长线于点H,且满足GB=GE.
(1)求证:HG是⊙O的切线;
(2)若GE=BE,HB=.
(i)求⊙O的半径;
(ii)如图2,连接AF,交弦BC于点M,若AF∥HG,求线段OD的长.
【解答】解:(1)连接OB,如图:
∵GB=GE,
∴∠GBE=∠GEB=∠CED,
∵GD⊥AC,
∴∠CED+∠ECD=90°,
∴∠GBE+∠ECD=90°,
∵OB=OC,
∴∠ECD=∠OBC,
∴∠GBE+∠OBC=90°,
∴OB⊥HG,
∴HG是⊙O的切线;
(2)(i)过G作GM⊥BC于M,如图:
∵GB=GE,GM⊥BC,
∴ME=BE,
∵GE=BE
∴=,
∴cos∠GEM=,
∴cos∠CED=,
∵AC为⊙O直径,
∴∠ABC=90°,
∴∠BAC=90°﹣∠C=∠CED,
∴cos∠BAC=,
设AB=k,则AC=k,BC=2k,
∵HG为⊙O切线,
∴∠C=∠HBA,
而∠H=∠H,
∴△HBA∽△HCB,
∴====,
∵HB=,
∴HC=,HA=,
∴AC=HC﹣HA=2,
∴⊙O的半径为;
(ii)连接CF,过F作FN⊥BC于N,如图:
由(i)知:AC=2,cos∠BAC=,
∴AB=2,BC=4,
∵AF∥HG,
∴∠AMB=∠GBC,
∵GB=GE,
∴∠GBC=∠GEM,
∴∠AMB=∠GEM,
∴cos∠AMB=cos∠GEM=,
Rt△ABM中,设BM=t,则AM=t,AB=2t,
∴2t=2,解得t=1,
∴BM=1,AM=,
∴CM=BC﹣BM=3,
∵BC与AF是⊙O的相交弦,
∴AM MF=BM CM,即 MF=1×3,
∴MF=,
Rt△FNM中,cos∠FMN=cos∠AMB=,
∴=,
∴MN=,ME=,
∴CE=CM﹣ME=,
Rt△CED中,cos∠CED=cos∠GEB=,
∴ED=,CD=,
∴OD=OC﹣CD=.
29.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E,连接AD,CD.
(1)求证:DE与⊙O相切;
(2)若AB=6,tanA=,求BE的长;
(3)线段AB,BE,CE之间有何数量关系?写出你的结论并证明.
【解答】(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE,
∵BE⊥DE,
∴OD⊥DE,
∴DE与⊙O相切.
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=6,tanA=,
∴BD=AD,
设AD=m,则BD=m,
∴m2+2m2=36,
∴m=2或﹣2(舍弃),
∴AD=2,BD=2,
∵BE⊥DE,
∴∠ADB=∠BED=90°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴△ABD∽△DBE,
∴=,
∴=,
∴BE=4.
(3)解:结论CE=AB﹣BE,
理由:过D作DH⊥AB于H,
∵BD平分∠ABC,DE⊥BE,
∴DH=DE,
在Rt△BED与Rt△BHD中,
,
∴Rt△BED≌Rt△BHD(HL),
∴BH=BE,
∵∠DCE=∠A,∠DHA=∠DEC=90°,
∴△ADH≌△CDE(AAS),
∴AH=CE,
∵AB=AH+BH,
∴AB=BE+CE,
∴CE=AB﹣BE.
30.如图,AB是⊙O的直径,AC是弦,点E在圆外,OE⊥AC于点D,BE交⊙O于点F,连接BD、BC、CF,∠BFC=∠AED.
(1)求证:AE是⊙O的切线;
(2)求证:OB2=OD OE;
(3)设△BAD的面积为S1,△BDE的面积为S2,若tan∠ODB=,求的值.
【解答】解:(1)证明:∵∠BFC=∠AED,
又∠BFC=∠BAC,
∴∠BAC=∠AED,
∵OE⊥AC于点D,
∴∠ADE=∠ADO=90°,
∴∠AED+∠EAD=90°,
∴∠BAC+∠EAD=90°,即∠OAE=90°,
∴OA⊥AE,
∴AE是⊙O的切线;
(2)∵∠OAE=∠ADO=90°,∠AOD=∠EOA,
∴△AOD∽△EOA,
∴,
∴OA2=OD OE,
∵OB=OA,
∴OB2=OD OE;
(3)∵AB为直径,
∴∠ACB=90°,
∵∠ADO=90°,
∴∠ACB=∠ADO,
∴OE∥BC,
∴∠ODB=∠DBC,
在Rt△BCD中,tan∠DBC=tan∠ODB==,
设DC=2m,则BC=3m,
∴OD=BC=,
∵OE⊥AC于点D,
∴AD=DC=2m,
∴OA=OB==,
由(2)知OB2=OD OE,
∴,
而∠BOD=∠EOB,
∴△BOD∽△EOB,
∴,
∴设S△BOD=9k,则S△EOB=25k,
∴△BDE的面积为S2=S△EOB﹣S△BOD=16k,
而△BAD的面积为S1=2S△BOD=18k,
∴==.
31.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.
(1)求证:AF为⊙O的切线;
(2)当点D为EF的中点时,求证:AD2=AO AE;
(3)在(2)的条件下,若sin∠BAC=,AF=2,求BF的长.
【解答】(1)证明:连接CD.
∵AC是直径,
∴∠ADC=90°,
∴∠DAC+∠ACD=90°,
∵∠ABD=∠ACD,∠DAF=∠ABD,
∴∠DAF=∠ACD,
∴∠DAF+∠DAC=90°,
∴∠FAC=90°,
∴AF为⊙O的切线.
(2)证明:∵∠FAE=90°,DF=DE,
∴AD=DE=DF,
∴∠DAE=∠AED,
∵OA=OD,
∴∠DAE=∠ADO,
∴∠ADO=∠AED,
∵∠OAD=∠DAE,
∴△ADO∽△AED,
∴=,
∴AD2=AO AE.
(3)解:过点B作BJ⊥EC于J.
∵AC是直径,
∴∠ABC=90°,
∴sin∠BAC==,
∴可以假设BC=a,AC=3a,
∵BJ⊥AC,
∴∠AJB=90°,
∴∠BAC+∠ABJ=90°,∠ABJ+∠CBJ=90°,
∴∠CBJ=∠BAC,
∴sin∠CBJ=sin∠BAC==,
∴CJ=a,
∴BJ===a,
∵DA=DE,
∴∠DAE=∠AED=∠CEB,
∵∠DAE=∠CBE,
∴∠CEB=∠CBE,
∴CE=CB=a,
∴EJ=EC﹣CJ=a﹣a=a,AE=AC﹣EC=2a,
∵AF∥BJ,
∴=,
∴=,
∴a=,
∴AE=2,EJ=,BJ=,
∴EF===6,BE===2,
∴BF=EF+BE=6+2=8.
32.如图1,O是△ABC的边BC的中点,⊙O与BC交于E、F两点,与AB相切于点D,连接AO交⊙O于点P,=.
(1)猜想AC与⊙O的位置关系,并证明你的猜想.
(2)如图2,延长AO交⊙O于Q点,连接DE、DF,DQ,FQ,FQ=,ED=5,求DQ的长.
(3)如图3,若DE=5,连接DF、DP、PF,设DP=x,△DPF的面积为y,求y与x之间的函数关系式.
【解答】解:(1)结论:AC与⊙O相切,
理由:过点O作OH⊥AC于H,
∵⊙O与AB相切于点D,
∴OD⊥AB,
∵,点O是圆心,
∴∠BOP=∠COP=90°,
又∵O是BC的中点,
∴AB=AC,
∴∠BAO=∠OAC,
又∵OD⊥AB,OH⊥AC,
∴OD=OH,
∴OH是半径,
∴AC与⊙O相切.
(2)如图2中,过点Q作QN⊥CD于N,QM⊥DE交DE的延长线于M,连接QE.
∵AO⊥BC,O是圆心,
∴PQ是直径,
∴OQ=OF,
∴FQ=OF=,
∴FO=,
∴EF=13,
∵EC是直径,
∴∠EDC=90°,
∵FD2=EF2﹣DE2,DE=5,
∴FD=12,
∵∠QDF=∠QOF=45°,
∴∠QDM=∠QDN=45°,
∴=,
∴EQ=FQ,
∵QM⊥DM,QN⊥DN,
∴QM=QN,
∵∠M=∠QNF=90°,
∴Rt△QME≌Rt△QNF(HL),
∴EM=FN,
∵∠M=∠MDN=∠DNQ=90°,
∴四边形DMQN是矩形,
∵QM=QN,
∴四边形DMQN是正方形,
∴DM=DN,
∴DE+DF=DM﹣EM+DN+NF=2DM=17,
∴DM=DN=,
∴DQ=DN=.
(3)如图3中,过点F作FH⊥DP交DP的延长线于H.
∵∠PDF=∠POC=45°,∠H=90°,
∴∠HDF=∠DFH=45°,
∴DH=FH,DF=FH,
∵∠EDF=∠H=90°,∠EFP=∠DFH=45°,
∴∠EFD=∠PFH,
∴△EFD∽△PFH,
∴==,
∵DE=5,
∴PH=,
∴DH=FH=x+,
∴y=S△PDF= DP FH,
∴y=×x×(x+)=x2+x(x>0).
33.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD∥AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:AF是⊙O的切线;
(2)求证:AB2﹣BE2=BE EC;
(3)如图2,若点G是△ACD的内心,BC BE=64,求BG的长.
【解答】解:(1)如图1,连接OA,
∵AB=AC,
∴=,∠ACB=∠B,
∴OA⊥BC,
∵CA=CF,
∴∠CAF=∠CFA,
∵CD∥AB,
∴∠BCD=∠B,
∴∠ACB=∠BCD,
∴∠ACD=∠CAF+∠CFA=2∠CAF,
∵∠ACB=∠BCD,
∴∠ACD=2∠ACB,
∴∠CAF=∠ACB,
∴AF∥BC,
∴OA⊥AF,
∴AF为⊙O的切线;
(2)∵∠BAD=∠BCD=∠ACB,∠B=∠B,
∴△ABE∽△CBA,
∴,
∴AB2=BC BE=BE(BE+CE)=BE2+BE CE,
∴AB2﹣BE2=BE EC;
(3)由(2)知:AB2=BC BE,
∵BC BE=64,
∴AB=8,
如图2,连接AG,
∴∠BAG=∠BAD+∠DAG,∠BGA=∠GAC+∠ACB,
∵点G为内心,
∴∠DAG=∠GAC,
又∵∠BAD=∠ACB,
∴∠BAD+∠DAG=∠GAC+∠ACB,
∴∠BAG=∠BGA,
∴BG=AB=8
