七年级上册第二章有理数

玉门二中七年级数学预习案
第1课 有理数 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1．理解有理数的意义，并能将给出的有理数进行分类；2．培养树立分类讨论的思想．
学习重点 有理数包括哪些数
学习难点 有理数的分类及其分类的标准．
预 习 案
（一）、从原有的认知结构提出问题1．什么是正、负数？2．如何用正、负数表示具有相反意义的量？数0表示量的意义是什么？举例说明．3．任何一个正数都比0大吗？任何一个负数都比0小吗？4．什么是整数？什么是分数？（二）、新课学习1．有理数概念:2．有理数的分类（三）、运用举例 变式练习1、完成课本议一议2、课本例1（四）课堂练习把下列各数填在相应的括号里(将各数用逗号分开)：1.5, -5, 0, 3, , , 100, -, -2.3 7, －11, 0.2, +, , 1, -1正整数集合：｛ …｝；负整数集合：｛ …｝；正分数集合：｛ …｝；负分数集合：｛ …｝．2、-100不是( )A．有理数 B．自然数 C．整数 D．负有理数(2)在以下说法中，正确的是( )A．非负有理数就是正有理数 B．零表示没有，不是有理数C．正整数和负整数统称为整数 D．整数和分数统称为有理数3、某地气象站测得某天的四个时刻气温分别为：早晨6点为零下3℃，中午12点为零上1℃，下午4点为0℃,晚上12点为零下9℃.1.用正数或负数表示这四个不同时刻的温度.2.早晨6点比晚上12点高多少度.3.下午4点比中午12点低多少度.小结本节课的内容是：
第2课 数 轴 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、通过与温度计的类比认识数轴,会用数轴上的点表示有理数; 2、借助数轴了解相反数的概念,知道互为相反数的一对数在数轴上的位置关系; 3、利用数轴比较有理数的大小.
学习重点 数轴、相反数的概念及应用。
学习难点 数形结合的数学思想和方法的渗透，利用数轴比较有理数的大小。
预 习 案
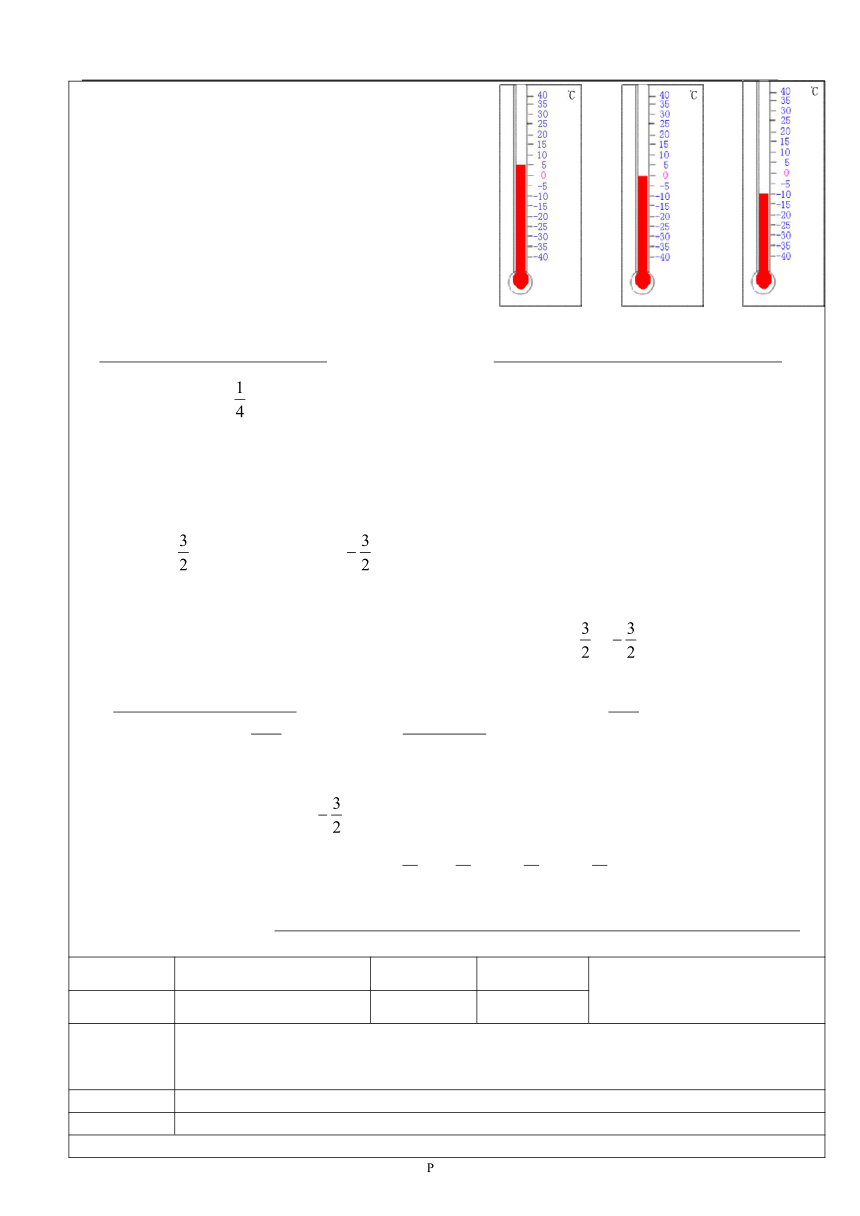
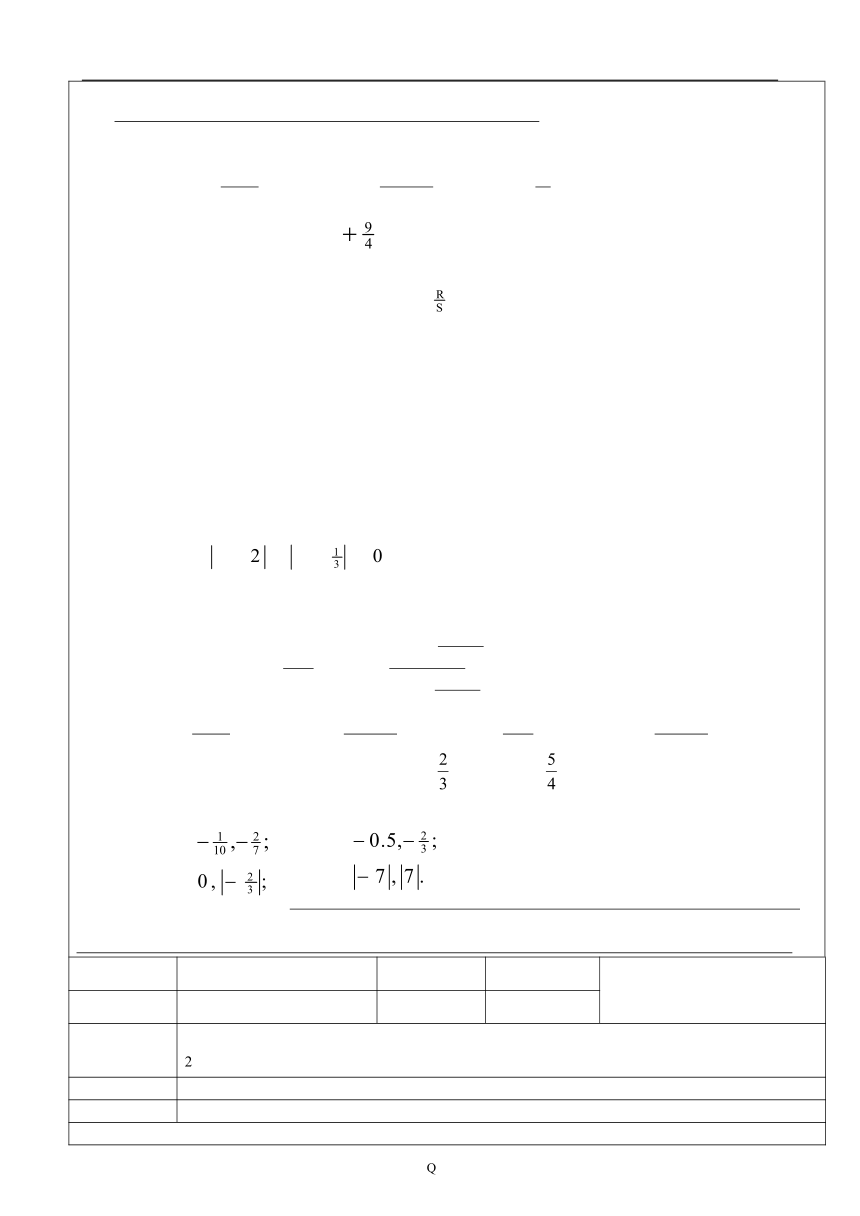
（一）自主学习1:温度计是我们日常生活中用来测量温度的重要工具，你会读温度计吗？请你尝试读出图中三个温度计所表示的温度？2：在一条东西向的马路上，有一个汽车站，汽车站东3 m和7.5m处分别有一棵柳树和一棵杨树，汽车站西3 m和4.8m处分别有一棵槐树和一根电线杆，试画图表示这一情境．（二）自主探究3、由上述两问题得到什么启发？你能用一条直线上的点表示有理数吗 4、 是数轴，数轴的三要素： 例题1； +3，-4，，-1.5，0分别在数轴的什么位置 2：指出数轴上 A, B, C, D各点分别表示什么数 3： 画出数轴，并用数轴上的点表示下列各数： ， -5， 0， 5， -4，4：2与-2有什么相同点与不相同点？它们在数轴上的位置有什么关系？与，5与-5呢？ 4、 称这两个数互为相反数，特别地，0的相反数是 。在数轴上，表示互为相反数的两个点，位于原点的 并且与原点的距离 。6、观察数轴并回答问题：问题1：数轴上的两个点，右边点表示的数与左边点表示的数有怎样的大小关系？问题2：正数、负数在数轴的什么位置？判断它们的大小？ 利用结论练习：比较下列每组数的大小，并说明理由.⑴-2 和 +6；⑵0和 -1.8；⑶和 -4.7、数轴上两个点所表示数，右边的总比左边的 .正数 0，负数 0，正数 负数.（三）自主检测练习册（四）小结本节课的内容是：
第3课 绝对值 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、借助数轴，理解绝对值的概念，求一个数的绝对值，利用绝对值比较两个负数的大小。2、通过运用“| |”来表示一个数的绝对值，培养学生的数感和符号感，达到发展学生抽象思维的目的；
学习重点 理解绝对值的概念；求一个数的绝对值；
学习难点 数形结合的数学思想和方法的渗透，利用数轴比较有理数的大小。比较两个负数的大小。
预 习 案
（一）自主学习1、 叫做这个数的绝对值。2、互为相反数的两个数的绝对值有什么关系 3、正数的绝对值是 ；负数的绝对值是 ；0的绝对值是 .
（二）自主探究例1　求下列各数的绝对值：-21， ， 0， -7.8。例2　比较下列每组数的大小：(1)-1和-5；(2) 和-2.7。
　　3、通过上面例子，引导学生归纳总结出一个数的绝对值与这个数的关系。
　　　　4．“做一做”：
　　(1)在数轴上表示下列各数，并比较它们的大小：-1.5，-3，-1，-5；
　　(2)求出(1)中各数的绝对值，并比较它们的大小；
　　(3)你发现了什么
6、讨论（1）字母 a 表示一个数，-a 表示什么？-a一定是负数吗？（2）已知： ，求2x+3y的值。（三）自主检测一个数的绝对值是它本身,那么这个数一定是 。2.绝对值小于3的整数有 个,分别是 。3.如果一个数的绝对值等于 4，那么这个数等于 。4.用>、<、=号填空： │-5│ 0 , │+3│ 0, +8│ │-8│ , │-5│ │-8│.5.在数轴上表示下列各数，并求它们的绝对值： ，6 ，-3 ，，0，-1，2；6.比较下列各组数的大小：
　　　　 (1) (2)
　　　　 (3) (4)
（四）小结本节课学习的内容： 。
第4课 有理数的加法（1） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、经历探索有理数加法法则的过程，理解有理数的加法法则；2、能熟练进行整数加法运算；
学习重点 有理数加法法则的探索过程，利用有理数的加法法则进行计算；
学习难点 异号两数相加的法则。
预 习 案
（一）自主学习1、足球比赛中赢球个数与输球个数是相反意义的量．若我们规定赢球为“正”，输球为“负”．比如，赢3球记为+3，输2球记为-2．学校足球队在一场比赛中的胜负可能有以下各种不同的情形：(1)上半场赢了3球，下半场赢了2球，那么全场共赢了5球．用算式表示： 。(2)上半场输了2球，下半场输了1球，那么全场共输了3球．用算式表示： 。你能说出其他可能的情形吗？． （二）自主探究1、如果我们把向东走5米记作+5米，那么-5米表示什么？ （1）一个人向东走5米，再向东走3米，两次一共走多少米？ 或说：一质点在数轴上先运动+5米，再运动+3米，两次一共运动多少米？ （2）一个人向东走5米，再向西走5米，两次一共走了多少米？ 或说：一质点在数轴上先运动+5米，再运动-5米，两次一共运动了多少米？ （３）一个人向东走５米，再向西走３米，两次一共走了多少米？ 或说：一质点在数轴上先运动＋５米，再运动－３米，两次一共运动了多少米？2、仔细观察比较上述算式，你发现了什么运算规律？2、有理数的加法法则： 例1 计算下列算式的结果，并说明理由：(1) 180 +(-10)； (2) (-10)+(-1)；（三）自主检测：1、用算式表示：温度－10℃上升了3℃达到_______. 2、一个数大于另一个数的绝对值，则这两个数的和是（ ）A.负数 B.正数 C.非负数 D.非正数3、某出租车司机小李某天下午营运全是在东西走向的人民大道上进行的， 如果规定向东为正，想西为负，他这天下午行车里程（单位：千米）如下：+15，-2，+5，-1，+10，-3，-2，+12，+4，-5，+6.（1）将最后一名乘客送到目的地时，小李距下午出车时的出发点多远？（2）若汽车耗油量为a升/千米，这天下午小李共耗油多少升？（四）小结本节课的内容： 。
第5课 有理数的加法（2） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、进一步熟练掌握有理数加法的法则；2、掌握有理数加法的运算律，并能运用加法运算律简化运算。
学习重点 有理数加法运算律，并能运用加法运算律简化运算；
学习难点 灵活运用运算律简化运算。
预 习 案
（一）自主学习1．叙述有理数的加法法则．2．小学学过的加法的运算律是不是也可以扩充到有理数范围？3．计算下列各题，并说明是根据哪一条运算法则？(1)(-9.18)+6.18= (2)6.18+(-9.18)= (3)(-2.37)+(-4.63)=4．计算下列各题：(1)[8+(-5)]+(-4)= (2)8+[(-5)+(-4)]= (3)[(-7)+(-10)]+(-11)= (4)(-7)+[(-10)+(-11)]= (5)[(-22)+(-27)]+(+27)= (6)(-22)+[(-27)+(+27)]=交换律——两个有理数相加，交换加数的位置， ．用代数式表示： 结合律——三个数相加，先把前两个数相加，或者先把后两个数相加， ．用代数式表示： 这里a、b、c表示任意三个有理数．（二）自主探究；例1 计算：16+(-25)+24+(-32)．例2、计算（1）；；（2）总结常用的三个规律：1、 一般地，总是先把正数或负数分别结合在一起 。2、有相反数的可先把相反数 ，能凑整的可先 。3、有分母相同的，可先把分母相同的数结合 。（三）自主检测1、计算：（1）（ —6）+8+（—4）+12； （2）（3） （4）（四）小结节课学习的内容： 。
第6课 有理数的减法 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 经历探索有理数的减法法则的过程，理解有理数的减法法则，并能熟练运用法则进行有理数的减法运算．
学习重点 理解有理数的减法法则；
学习难点 能熟练运用法则进行有理数的减法运算．
预 习 案
（一）自主学习1、乌鲁木齐的最高温度为4℃，最低温度为-3℃，这天乌鲁木齐的温差为多少？你是怎么算的？2、在一个比赛用的跳水馆里，有10米跳台，3米跳板，如果以水面为基准，那么10米跳台可表示为+10米，3米跳板可表示为+3米，如果水深是4米，则可用（ ）米表示：1.跳台与跳板的距离可表示为：（ ）米－（ ）米=（ ）米.也可以表示为：（ ）米+（ ）米=（ ）米.2.从10米跳台到水底的距离可表示为：（ ）米－（ ）米=（ ）米.也可以表示为：（ ）米+（ ）米=（ ）思考：通过上面填空，你能总结有理数减法法则吗？ 。 （二）自主探究问题1：你能从温度计上看出4℃比－3℃高多少摄氏度吗？如何计算4－（－3）呢？总结：1.有理数的减法运算法则: ；字母表示： ；2.转化的思想方法:减法运算转化成 进行计算 例1．计算 :(1) (-3)-（-5）= （2） 0 – 7= 例2．计算（1） 7.2 - (-4.8)= (2) (-3 －2 ) - 5 =例3 世界上最高的山峰是珠穆朗玛峰，其海拔高度大约为是8848米，吐鲁番盆地的海拔高度大约是－155米，两处高度相差多少米？（三）自主检测1、一个数加-3.6，和为-0.36，那么这个数是（ ） A.-2.24 B.-3.96 C.3.24 D.3.962、下列计算正确的是（ ） A.（-14）-（+5）= -9 B. 0-（-3）=3 C.（-3）-（-3）= -6 D.|5-3|= -（5-3）3、较小的数减去较大的数，所得的差一定是（ ） A.零 B.正数 C.负数 D.零或负数4、下列结论正确的是 （ ）A、数轴上表示6的点与表示4的点两点间的距离是10；B、数轴上表示-8的点与表示-2的点两点间的距离是-10C、数轴上表示-8的点与表示-2的点两点间的距离是10 D、数轴上表示0的点与表示-5的点两点间的距离是-55、下列结论中，正确的是 （ ）A、有理数减法中，被减数不一定比减数大；B、减去一个数，等于加上这个数C、零减去一个数，仍得这个数 D、两个相反数相减得06、（1）温度3℃比 -8℃高 ； （2）温度-10℃比-2℃低 ；（3）海拔-10m比-30m高 ；7、计算： （1）（+5）-（-3）； （2） （-3）-（+2） （3）（-20）-（-12）； （4）（-1.4）-2.6； （5） -（-）； （6）（-）-（-）.8、已知a=, b=, c=,求代数式a－b－c的值.（四）小结本节课的少内容： 。
第7课 有理数的加法混合运算（1） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1．熟练地进行有理数加减混合运算，并利用运算律简化运算．2．灵活运用有理数运算法则进行加减混合运算．熟练掌握有理数的加减混合运算及其运算顺序．3．能根据具体问题，适当运用运算律简化运算．
学习重点 熟练掌握有理数的加减混合运算及其运算顺序．
学习难点 根据具体问题，适当运用运算律简化运算．
预 习 案
（一）自主学习1、写出-6+9-8-7+3两种读法 ；2、按课本43的游戏规则看谁最终获胜。写出计算过程 ；（二）自主探究例1、 计算：(1)( -)+ - = (2)(-5)- (- )+ 7- =总结：1．通过本节课的学习研究，我们进一步巩固和掌握有理数的加减混合运算，并能根据具体问题适当运用 律和 律简化运算． 2．在加减运算时，适当运用 律，把正数与负数分别相加，可使运算简便．但要注意交换加数的位置时，要连同前面的 交换． 星期一二三四五六日气温度化/℃2－1－24－2.510.5例2、某气象员为了掌握一周内天气的变化情况，测量了一周内的气温．下表是一周内气温变化情况(用正数表示比前一日上升数，用负数记下降数字)试分析这个星期气温的总体变化情况．（三）自主检测1、填空题： 计算题（1） （2）选择合适的算法完成下面题目（1） （2）（3） （4）（四）小结本节课学习的内容： 。
第8课 有理数的加法混合运算（2） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、理解有理数的加减法可以互相转化，并了解代数和概念；2、熟练地进行有理数的加减混合运算；
学习重点 熟练掌握有理数的加减混合运算及其运算顺序．
学习难点 并了解代数和概念；熟练地进行有理数的加减混合运算。
预 习 案
（一）自主学习（1）叙述有理数加法法则． （2）叙述有理数减法法则． （3）符号“+”和“-”各表达哪些意义？ （4）化简：+(+3)= +(-3)= -(+3)= -(-3)= （二）自主探究1、看课本44页：一架飞机进行特技表演，飞行的高度变化由表格给出。写出飞机比起飞点高了多少米的计算过程：对于题中的“高度变化”，你是怎么理解的？ 2、完成例1、计算：（1）（- ）- 15 + (- ) (2) (-12)- (- )+ (- 8)- （三）课堂检测１、a，b，c，d在数轴上的对应点如图所示，且|a|=|b|，|d|>|c|>|a|，下列各式正确的是（ ） A.a+b>c B.c+a>b C.d+c>a D.b+c>0 2、若|a-1|+|b+3|=0，则b-a-的值是 （ ） A.-4 B.-2 C.-1 D.1 3、（1）-3减去4与-3的和所得的差是多少？ （2）-6，-3.5，4三数的和比这三数的绝对值的和小多少？ （3）求-1，+2，-3，+4，-5，…，-99，100，这100个数的和. （4）已知甲地高度是-10m，甲地比乙地高10m，又乙地比丙地高6m，求甲地比丙地高多少？4、．计算：（1） （2）-2.25+ (3)（四）小结本节课学习的内容：
第9课 有理数的加法混合运算（3） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、能综合运用有理数及其加、减法的有关知识灵活地解决简单的实际问题。2、运用图表描述事物的变化，会用折线统计图表示数据变化趋势。
学习重点 熟练掌握有理数的加减混合运算及其运算顺序．
学习难点 运用有理数及其加、减法的有关知识灵活地解决简单的实际问题。
预 习 案
（一）自主学习看课本47页如果把流花河的警戒水位记为0点，那么其他数据可以分别记为什么？（二）合作交流1、下表是小明记录的今年雨季沙河一周内的水位变化情况（上周末的水位达到警戒水位）。星期一二三四五六日水位变化/米+0.2+0.81-0.35+0.03+0.28-0.36-0.01 注：正号表示水位比前一天上升，负号表示水位比前一天下降。（1）本周哪一天沙河的水位最高？哪一天水位最低？它们位于警戒水位之上还是之下？与警戒水位的距离分别是多少？(2)与上周末相比,本周末沙河水位是上升了还是下降了 (3)请完成下面的本周水位记录表:（自编数据）星 期 一二三四五六日水位记录（米） 33.6(4)以警戒水位为0点,用折线统计图表示本周的水位情况。（三）自主检测1、玉门二中初一(2)班学生的平均身高是160厘米.(1)下表给出了该班6名同学的身高情况(单位:厘米).试完成下表:姓名小明小彬小丽小亮小颖小山身高159154165身高与平均身高的差-1+20+3(2)谁最高 谁最低 (3)最高与最矮的学生身高相差多少 2、某一河段的警戒水位为50.2米，最高水位为55.4米，平均水位为43.5米，最低水位为28.3米，如果取警戒水位作为0点，则最高水位为 ，平均水位为 最低水位为 （高于警戒水位取正数）3、一个加数是6，和十-9，另一个加数是 4、从-1中减去-与的和，列式为： ，所得的差是 。（四）小结本节课学习的内容：
第10课 有理数的乘法（1） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 学会有理数的乘法运算，掌握确定多个不等于零的有理数相乘的积的符号方法以及有一个数为零积是零的情况。
学习重点 有理数的乘法法则，了解倒数的概念
学习难点 有理数的乘法法则，了解倒数的概念
预 习 案
（一）自主学习（１）观察课本49页给出的图片，分析教科书提出的问题，弄清题意，明确已知是什么，所求是什么，思考如何解答. （２）如果用正号表示水位上升，用负号表示水位下降，讨论四天后，甲水库水位的变化量的表示法和乙水库水位变化量的表示法. （１）由课题引入中知道：４个－３相加等于－１２，可以写成算式（－３）×４＝－１２，那么下列一组算式的结果应该如何计算？请你思考：（－３）×３＝＿＿＿＿;（－３）×２＝＿＿＿＿;（－３）×１＝＿＿＿＿;（－３）×０＝＿＿＿.（２）当同学们写出结果并说明道理时，让学生通过观察这组算式等号两边的特点去发现积的变化规律，然后再出示一组算式猜想其积的结果：（－３）×（－１）＝＿＿＿； （－３）×（－２）＝＿＿＿;　　　 （－３）×（－３）＝＿＿＿; （－３）×（－４）＝＿＿＿.有理数乘法法则： （二）自主学习例１.计算：⑴（－４）×５= 　　 ⑵（－５）×（－７）=　⑶（－）×（－）= ⑷（－3）×（－）=“议一议”：几个有理数相乘，因数都不为零时，积的符号怎样确定？有一个因数为零时，积是多少？（－１）×２×３×４＝＿＿＿＿＿;（－１）×（－２）×３×４＝＿＿＿＿＿;（－１）×（－２）×（－３）×４＝＿＿＿＿＿;（－１）×（－２）×（－３）×（－４）＝＿＿＿＿＿;（－１）×（－２）×（－３）×（－４）×０＝＿＿＿＿＿.结论：多个数相乘，积的符号由 的个数决定，当 时，积的 ；当 时，积的 .只要 ，积就为零.（三）课堂检测　一、选择题　　1．下面说法中正确的是（ ）　　A．因为同号相乘得正，所以（－2）×（－3）×（－1）＝6　　B．任何数和0相乘都等于0　　C．若，则 　　D．以上说法都不正确　　2．两个数相乘，同号得___________，异号得_________，并把_________相乘；　　3．一个数和任何数相乘都得0，则这个数是_________；　　4．若干个有理数相乘，其积是负数，则积中负因数的个数是_________数．　　5．计算：⑴（－8）×21÷4　；　　　　　　　⑵4÷5×（－25÷6）×（－7÷10）；⑶2÷3×（－5÷4）；　　　　　　　　⑷（－24÷13）×（－16÷7）×0×4÷3；⑸5÷4×（－1.2）×（－1÷9）；　 　⑹（－3÷7）×（－1÷2）×（－8÷15）.（四）小结本节课学习的内容：
第11课 有理数的乘法（2） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、学会运用乘法运算律简化计算的方法。2、会用文字语言和符号语言表述乘法运算律。
学习重点 有理数的乘法法则，了解倒数的概念
学习难点 运用乘法运算律简化计算。
预 习 案
（一）自主学习（1）根据有理数乘法法则，计算下列各题，并比较它们的结果：⑴（-７）×８与８×（-７）； ⑵［（-４）×（-６）］×５与（-４）×［（-６）×５］；⑶（-２）×［（-３）＋（-3÷2）］与（-２）×（-３）×（-２）×（-3÷2）；（２）通过计算积的比较，猜想乘法运算律在有理数范围内是否适用。乘法的交换律： ；乘法的结合律： ；乘法对加法的结合律： 。（二）自主探索下列等式成立吗 为什么 (1) (-765)×4=4×(-765); (2) [7×(-8)] 3=7 ×[(-8) ×3];(3) (-5) ×[1/2+(-1/3)]= (-5) ×1/2+(-5 )×(-1/3) .你能用字母表示乘法运算律吗 4、倒数(1)定义： 互为倒数．即： a、b互为倒数。举例 与 ； 与 (2)倒数是它本身的数有： (3)0的倒数：0没有倒数．(4)写出互为倒数的两个数的特征． 例３，计算：用两种方法计算，并比较哪种方法较简便。⑴（－＋）×（－24）　　　　　　　　　　　　⑵　（－7）×（－）×（三）自主检测１、计算：　　⑴　０×（－）　；　　　　⑵３×（－）；⑶（－３）×０.３　；　　　 ⑷（－）×（－）；２、计算：⑴（－）×（－８）；　　　　　 ⑵３０×［（－）－］；⑶　（０.2５－）×（－３６）； ⑷８×（－）×（四）小结本节课学习的内容：
第12课 有理数的除法 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 学会进行有理数的除法运算；掌握多个数相乘；商的符号判定方法.
学习重点 发现有理数除法的法则，会进行有理数的除法运算.
学习难点 会用“除以一个数等于乘以它的倒数”法则进行有理数的除法运算，提高灵活解题的能力.
预 习 案
（一）自主学习1、已知两个因数的积和其中一个因数，要求另一个因数，应该用什么运算进行计算呢？ 2、问题1：8÷4是什么运算？商等于多少？ ； 问题2：0÷4等于多少？ ；问题3：（－12）÷（－3）是什么运算？商等于多少？ 3、在活动（1）的基础，请同学们想一想，分析讨论计算以下各题：⑴（－18）÷6= ； ⑵ 5÷（－1÷5）= ；⑶（－27）÷（－9）= ； ⑷ 0÷（－2）= .4、观察以上算式，看看商的符号及商的绝对值与被除数和除数有何关系？如果有，请大家从特例中归纳猜想出一般规律，并用自己的语言叙述规律.（二）自主探索例1：计算：⑴（－15）÷（－3）； ⑵（－12）÷（－）；⑶（－0.75）÷0.25 ； ⑷（－12）÷（－）÷（－100）.做一做计算： ⑴1÷（-2/5）； 1×（－5/2）；⑵0.8÷（－3/10）； 0.8×（－10/3）；⑶（－1/4）÷（－1/60）； （－1/4）×（－60）.（2）计算出结果后，请同学们比较每一组小题中两个结果，并用语言叙述其中的规律. （3）想一想：负数的倒数如何求？ （三）课堂检测1、计算：⑴（－64）÷4； ⑵（－3÷5）÷（－3）； ⑶ 0÷（－16）； ⑷（－15）÷（－1÷5）÷（－2） （5）（－18）÷6; （6）（－63）÷（－7）； 2、下列说法正确的是（ ）A.几个有理数相乘，当因数有奇数个时，积为负 B.几个有理数相乘，当正因数有奇数个时，积为负C.几个有理数相乘，当积为负数时，负因数有奇数个 D.几个有理数相乘，当负因数有偶数个时，积为负3、如果两数之和等于零，且这两个数之积为负数，那么这两个数只能是（ ）A.两个互为相反数的数 B.符号不同的两个数 C.不为零的两个互为相反数的数 D.不是正数的两个数（四）小结本节课学习的内容：
第13课 有理数的乘方（1） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 掌握有理数乘法的概念，能进行有理数的乘方运算.
学习重点 理解有理数乘方的意义，掌握有理数乘方的概念，学会有理数乘方的运算。
学习难点 学会有理数乘方的运算。
预 习 案
（一）自主学习1、观察教科书给出的图片，阅读理解教科书提出的问题，弄清题意，计算每一次分裂后细胞的个数，五小时经过十次分裂后细胞的个数是 .2、乘方的有关概念．(1) 叫乘方，乘方的结果叫 ． 叫底数， 叫指数，an读作： ．(2)乘方的意义：an表示 ．(3)写法的注意：当底数是负数或分数时，底数一定要 ．如：()2＝()×()，表示两个 相乘．而＝，表示2个2相乘的积除以3的 ．2．3、an与－an的区别．(1)an表示 ，读作： ．(2)－an表示 ，底数是 ，指数是 ，读作：a的n次方的 ．如：(－2)3底数是－2，指数是3，读作 的3次方，表示 相乘．而－23底数是2，指数是3，读作 ．3．乘方运算的符号规律．(1)正数的任何次幂都是 ．(2)负数的奇次幂是 ．(3)负数的偶次幂是 ．(4)0的奇数次幂，偶次幂都是 ．所以，任何数的偶次幂都是 ．4．乘方如何运算：乘方运算就是根据乘方的意义把它转化为 进行计算．举例 （二）自主探究例1计算：① 53= ② （-3）4= ③ （-1/2）3.=例2计算：102，103，104；②（-10）2，（-10）3，（-10）4.（三）自主检测（1）（-2）10的底数是_______，指数是________，读作_________(2)(-3)12表示______个_______相乘,读作_________,(3)( 1/3)8的指数是________,底数是________读作_______,(4)3.65的指数是_____,底数是____,读作______,xm 表示____个____相乘,指数是____,底数是____,读作______.（四）小结本节课学习的内容：
第14课 有理数的乘方（2） 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 1、通过实例感受有理数的乘方运算，当底数大于1时，幂增大的很快.2、熟练掌握有理数的乘方运算.3、参与折纸操作数学活动，在具体的情境中初步掌握估算的方法，获得一些经险。
学习重点 理解有理数乘方的意义，掌握有理数乘方的概念，学会有理数乘方的运算。
学习难点 进一步熟练有理数乘方的运算的技能.
预 习 案
（一）自主学习阅读教科书第87页读一读栏目“棋盘上的学问”中的第一自然段后，提出问题：棋盘里的米有多少呢？棋盘上的米究竟有多少 第2格有_______粒米,第3格有_______粒米,第4格有_______粒米,… … … …第64格有_______粒米，共有_______粒米.假设10000粒米为1斤，100斤为1袋，估计有 袋（二）自主探究1折纸活动，一边折，一边思考以下问题：纸的厚度为0.1mm ,对折一次后,厚度为2*0.1mm,对折两次后,厚度为多少毫米 对折20次后,厚度为多少毫米 若每层楼高度为3米,这张纸对折20次后约有多少层楼高 通过活动,你从中得到了什么启示 例3计算：①； ②； ③； ④ （三）自主检测1、填空：（1）310的意义是 个3相乘. （2） 平方等于它本身的数是 .立方等于它本身的数是 . （3） 一个数的15次幂是负数，那么这个数的2003次幂是 . （4）(－2)6中指数是 ，底数是 . （5）平方等于1/64的数是 ，立方等于1/64 的数是 .2、在-|-4|，-（-4），（-4），-4，最大的数是（　　　）　A.-|-4| B.-（-4） C.（-4） D.-43、设a<0，则下列说法中正确的是（ ） A.a的偶次方的偶次方是负数 B.a的奇次方的偶次方是负数 C.a的奇次方的奇次方是负数 D.a的偶次方的奇次方是负数4、如果a≠0，那么下列各式中一定成立的是（ ）A.-a>0 B.a-a>0 C.a-a>0 D.（-a）>05、计算：⑴ (－1/3 )3 ； ⑵ －32×23； ⑶ (－3)2×(－2)3⑷ －2×32； ⑸ (－2×3)2； ⑹ (－2)14×(－1/2)15；（四）小结本节课的内容：
第15课 10、科学记数法 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 借助身边熟悉的事物进一步体会大数，并会用科学记数法表示大数。
学习重点 能用科学记数法表示大数
学习难点 对科学记数法法则的理解。
预 习 案
（一）、自主学习1、你能列举生活中的较大数据吗？ 2、请同学们看下面的问题（a）2008年北京奥运会体育场——“鸟巢”能容纳91 000位观众。(b) 2008年5月12日，在我国四川省汶川县发生里氏8.0级强烈地震，面对地震灾难，各级政府共投入抗震救灾资金22 600 000 000元人民币。(c) 台风云娜的登陆给温州人民造成的经济损失超过100亿元从上面的问题中，你发现这些数据有什么特点？ 二、自主探究1、回顾有理数的乘方运算，算一算：10＝ 10＝ 108＝ 10＝ 想一想：1021表示什么？指数与运算结果中的0的个数有什么关系？与运算结果的数位有什么关系？一般地，10的n（n为正整数）次幂，在1的后面有 个0。课堂练习：把下列各数写成10的幂的形式：100 000＝ 　10 000 000＝ 　1 000 000 000＝ 2、我们可以借助10的幂的形式把一个比10大的数表示成整数段位是一位数的数乘以10n的形式。试试看10=1× 3 000=3× 25 000=2.5× 1 300 000 000＝1.3× ， 69 600 000 000＝6.96× ，98 000 000＝ ，10 100 000 000＝ ，3、科学记数法：一个大于10的数可以表示成 的形式，其中1≤a＜10，n是正整数，这种记数方法叫做科学记数法。4、想一想：用科学计数法表示一个大于10的数，10的次数n与原数的整数位数有何关系？用科学计数法计数有何优点？ （三）自主检测1、试一试：你能把下列各数用科学记数法表示吗？（1）6 900= （2）57 000 000= （3）123 000 000 000= 2、练一练 ： 你能把下列各数用科学记数法表示吗？(1)水星的半径为2 440 000米 (2)木星的赤道半径约为71 400 000米 (3)地球上的陆地面积约为149 000 000米 (4)地球上海洋面积大约为361 000 000平方千米 (5)地球质量为5 976 000 000 000 000 000 000吨 (6)地球的表面积大约为510 000 000平方千米 3、例：下列科学记数法表示的数的原数是什么？ （1）3.4×104 = （2）6×105= 思考：原数整数的位数与10的次数n有什么关系？ 4、、下列用科学记数法表示的数，原来各是什么数？（1）山东省面积大约为1.5×105平方千米 ； （2）人体中大约有2.5×1013个红细胞 ；（3）中国的森林面积大约为1.286×108公顷 ；（4）北京故宫的占地面积大约为7.2×105平方米 ；（5）全球每年大约有5.77×1014立方米的水从海洋和陆地转化为大气中的水蒸汽 ；5、用科学计数法表示正确的是（ ）(A) 300 000 000 =308 （B） 9 600 000=9.6×106 (C) 218.4亿=0.2184×1011 （D）293 000 000=2.93×109 （四）：小结本节课的内容：
第16课 11．有理数的混合运算 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 掌握有理数混合运算法则，能熟练进行四步以内有理数的混合运算，并能进行简便运算.
学习重点 掌握有理数混合运算法则，并能熟练地掌握有理数加、减、乘、除、乘方的混合运算。
学习难点 能在运算中合理使用运算规律简化运算。
预 习 案
（一）自主学习（1）有理数的加、减、乘、除四则运算的法则如何叙述？ （2）计算 ⑴1/2－1/2＋4/5; ⑵（－5/6＋3/8）×（－24）;⑶8÷（－4/9）÷18/5; ⑷－（－2/3）3 .（3）观察下列各题，各包含了哪几种运算？这种运算应该怎么进行？ ⑴ 18－6÷（－2）×（－1/3）; ⑵ 3＋22×（－1/5）; ⑶（－3）2×［－2/3＋（－5/9）］.（二）自主探究1、例题学习例1　计算：例2　计算： 24÷3+22×(-1/4)2、阅读“24点游戏规则”“从一副扑克牌（去掉大、小王）中任意抽取4张，根据牌面上的数字进行混合运算（每张牌只能用一次），使得运算结果为24或－24.其中红色扑克牌代表负数，黑色扑克牌代表正数，J、Q、K分别代表11、12、13”.任意抽出四张牌，写出结果为24的算式（至少写出3个） （三）自主检测⑴18－6＋（－2）×（－1/3）； ⑵3＋22×（－1/5）； ⑶（－3）2×［－2/3＋（－5/9）］.（4）由学生独立完成教科书第89页随笔练习 计算：⑴8＋（－3）2×（－2）； ⑵100÷（－2）2－（－2）÷（－2/3）. （四）小结本节课的内容：
第17课 第二章 回顾与思考 授课时间 课前审核年 月 日
备 课 人 学生姓名
学习目标 有理数及其运算
学习重点 掌握有理数混合运算法则，并能熟练地掌握有理数加、减、乘、除、乘方的混合运算。
学习难点 有理数及其运算和在实际生活中的应用
预 习 案
（一）自主学习回顾本章知识（用知识结构图表示）（二）自主探索完成课本总复习题（三）自主检测一、选择题1．若，，则有( ) ．A．　　B．　　C．　　D． 2．已知，当时，，当时，的值是( ) ．A．-17　　B．44　　C．28　　D．173．如果，那么的值为( ) ．　A．0　　B．4　　C．－4　　D．24．代数式取最小值时，值为( ) ．　A．　　B．　　C．　　D．无法确定5．六个整数的积，互不相等，则 ( ) ．　A．0　　B．4　　C．6　　D．86．计算所得结果为() ．　A．2　　B．　　C．　　D． 二、填空题1．有理数混合运算的顺序是__________________________．2．已知为有理数，则_________0，_________0，_______0．3．平方得16的有理数是_________，_________的立方等于－8．4．__________；计算：=_________。5．一个负数减去它的相反数后，再除以这个负数的绝对值，所得商为__________．6、已知，则=_________。7、因为到点2和点6距离相等的点表示的数是4，有这样的关系，那么到点100和到点999距离相等的数是____；到点距离相等的点表示的数是_____；到点m和点–n距离相等的点表示的数是____。8、已知点4和点9之间的距离为5个单位，有这样的关系，那么点10和点之间的距离是____________；点m和点n（数n比m大）之间的距离是_____________。三、解答题1．计算（1）；　　（2）；　　（3）；（4）；　　 （5）；（6）；　（7） （四）课堂小结（五）课后补充一、选择题（本大题共15小题，共45分）：1、在–1，–2，1，2四个数中，最大的一个数是（ ）（A）–1 （B）–2 （C）1 （D）22、有理数的相反数是（ ）（A） （B） （C）3 （D） –33、有理数–3的倒数是（ ）（A）–3 （B） （C）3 （D）4、如果两个有理数的积是正数，和也是正数，那么这两个有理数（ ）（A）同号，且均为负数 （B）异号，且正数的绝对值比负数的绝对值大（C）同号，且均为正数 （D）异号，且负数的绝对值比正数的绝对值大5、计算的结果是（ ）（A） （B） （C） （D）6、大于–3.5，小于2.5的整数共有（ ）个。（A）6 （B）5 （C）4 （D）37、已知数在数轴上对应的点在原点两侧，并且到原点的位置相等；数是互为倒数，那么的值等于（ ）（A）2 （B）–2 （C）1 （D）–18、如果，那么a是（ ）（A）0 （B）0和1 （C）正数 （D）非负数二、填空题：（本大题共5小题，共15分）9、如果向银行存入人民币20元记作+20元，那么从银行取出人民币32.2元记作________。10、比较大小：–π________–3.14（填=，＞，＜号）。11、计算：=___________。。13、一个数的倒数等于它的本身，这个数是_____________。三、解答题：（本大题共6个小题，共40分）14、（本题6分）在数轴上表示下列各数：0，–2.5，，–2，+5，。15、（本题12分）直接写出答案：（1）=____________； （2）=____________；（3）=____________； （4）_______________；（5）=_______________； （6）=_________。16、（共22分）计算下列各题（要求写出解题关键步骤）：（1）（4分） （2）（本题6分）（3）（本题6分）（4）（本题6分）（5）
PAGE
19