全等三角形的判定SAS
图片预览



文档简介
(共17张PPT)
11.2.2 三角形全等的判定(2) (SAS)
知识回顾:
判定三角形 全等的方法:
1.定义(重合)法;
2.边边边(SSS)
画出一个△ABC,使得AB=3cm, ∠B=30°,
BC=5cm,把你画的三角形剪下来,并与小组内其他同
学画的进行比较,它们会全等吗?
探究活动:
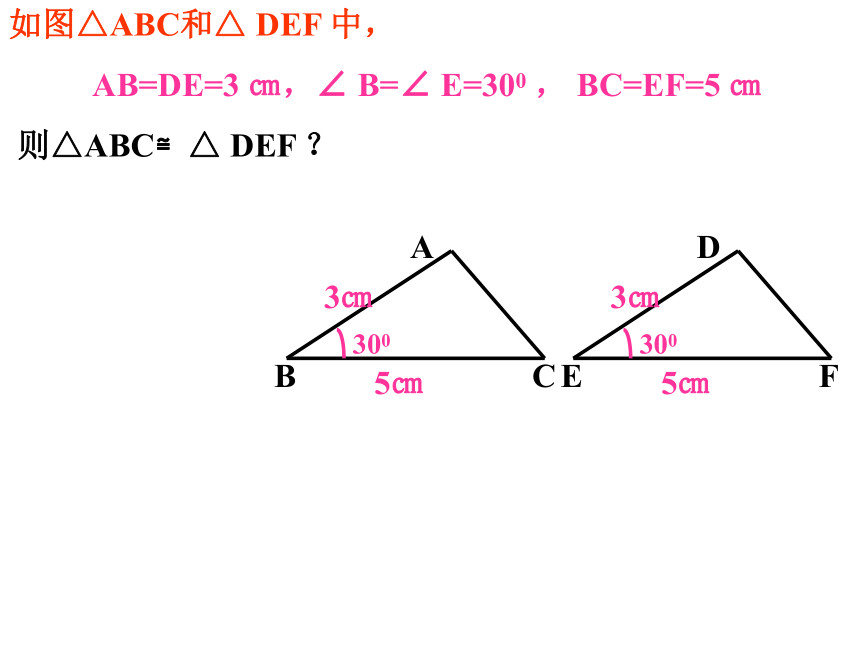
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则△ABC≌△ DEF ?
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
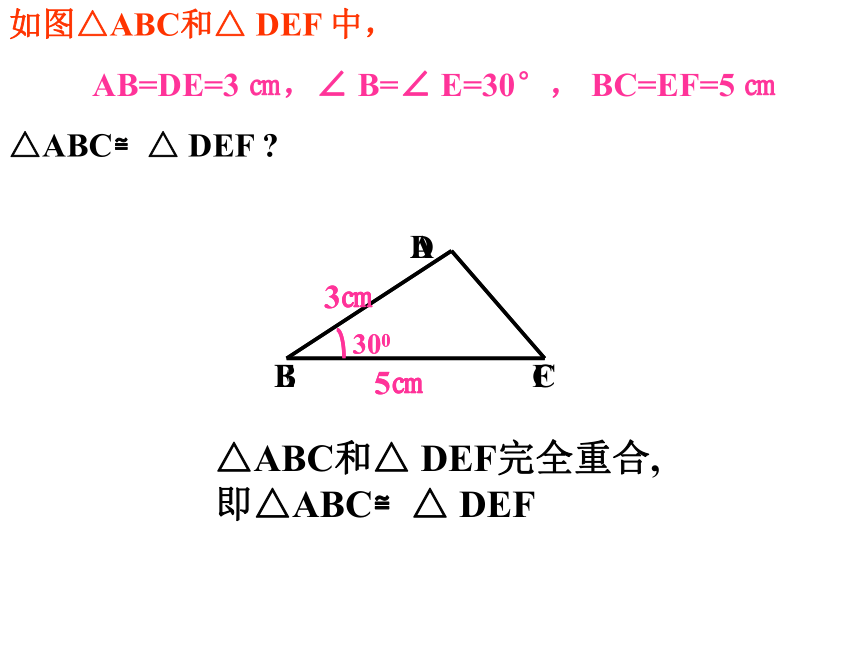
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=30°, BC=EF=5 ㎝
△ABC≌△ DEF
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
△ABC和△ DEF完全重合,
即△ABC≌△ DEF
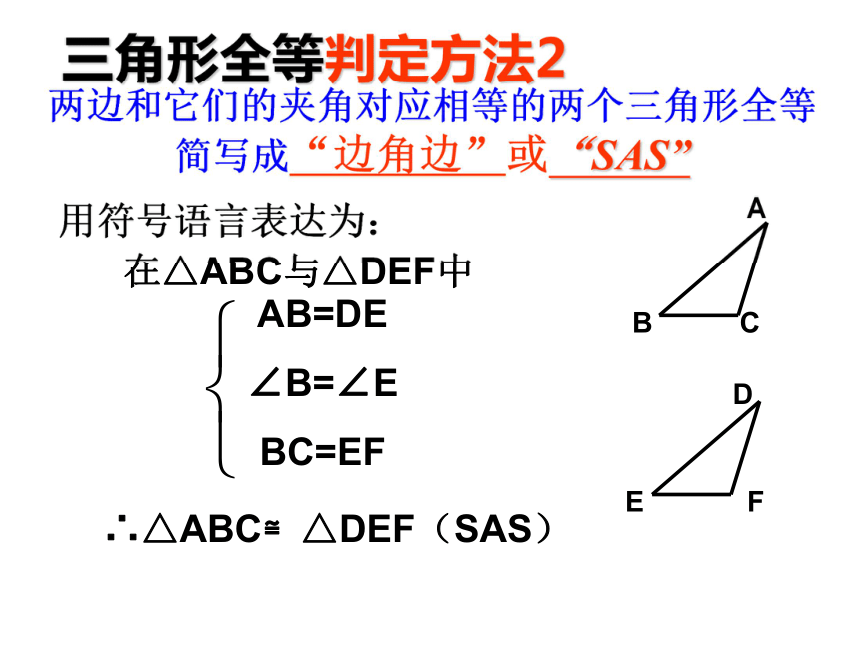
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等 简写成“边角边”或“SAS”
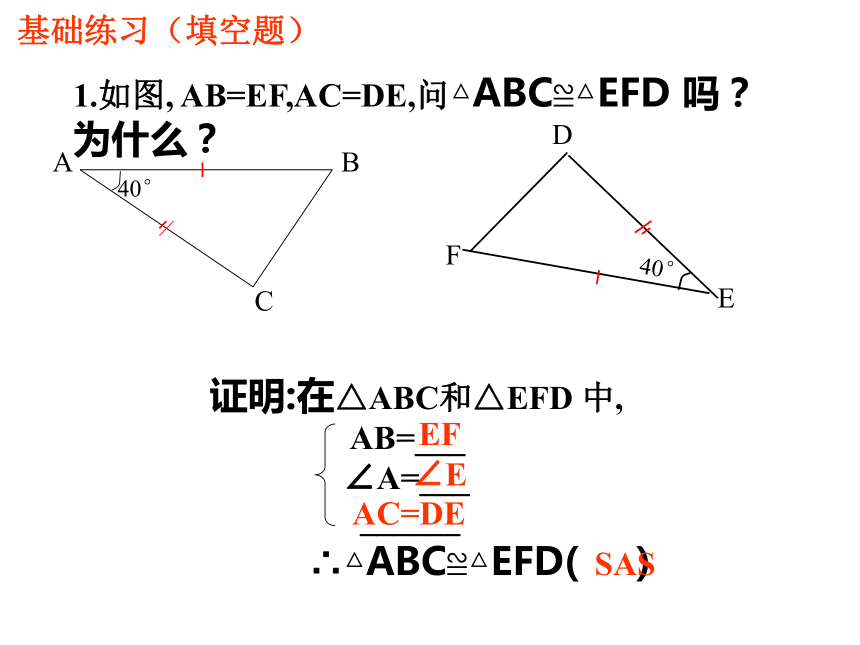
1.如图, AB=EF,AC=DE,问△ABC≌△EFD 吗?为什么?
A
B
C
40°
D
40°
E
F
证明:在△ABC和△EFD 中,
AB=___
∠A=___
______
∴△ABC≌△EFD( )
EF
∠E
AC=DE
SAS
基础练习(填空题)
A
B
C
D
O
2.如图AC与BD相交于点O,
已知OA=OC,OB=OD,
求证:△AOB≌△COD
证明:
在△AOB和△COD中
OA=OC
______________
OB=OD
∠AOB=∠COD
∴△AOB≌△COD( )
SAS
已知:如图,AB=CB,∠1=∠2
求证:∠A=∠C
例1
A
B
C
D
1
2
证明:
在△ABD 和△CBD中
AB=BC
∠1=∠2
BD=BD
∴△ABD≌△CBD(SAS)
∴ ∠A=∠C (全等三角形的对应角相等)
例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?
A
B
C
E
D
证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴ AB=DE(全等三角形的对应边相等)
CA=CD
∠ACB=∠DCE
CB=CE
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。
由前边两个题目可以看出:
归纳
1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?
B
D
A
C
证明:∵在△BAD和△BAC中,
BA=BA
∠BAD=∠BAC
AD=AC
∴ △BAD≌△BAC (SAS).
即BD=BC
2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠D
A
D
B
E
F
C
【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE
在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC
∴ △BAD≌△BAC (SAS).
即∠A=∠D
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
探究4
画出一个△ABC,使得AB=5cm, ∠B=30°,
AC=3cm,把你画的三角形与其他同学画的进行比较,它们会全等吗?
A
B
C
D
如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B
他们全等吗?
强调:这个角一定要是这两边所夹的角
到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是:
1、边边边(SSS)
2、边角边(SAS)
小结:
作业
P15 第3题
P16 第10题
11.2.2 三角形全等的判定(2) (SAS)
知识回顾:
判定三角形 全等的方法:
1.定义(重合)法;
2.边边边(SSS)
画出一个△ABC,使得AB=3cm, ∠B=30°,
BC=5cm,把你画的三角形剪下来,并与小组内其他同
学画的进行比较,它们会全等吗?
探究活动:
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则△ABC≌△ DEF ?
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=30°, BC=EF=5 ㎝
△ABC≌△ DEF
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
△ABC和△ DEF完全重合,
即△ABC≌△ DEF
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等 简写成“边角边”或“SAS”
1.如图, AB=EF,AC=DE,问△ABC≌△EFD 吗?为什么?
A
B
C
40°
D
40°
E
F
证明:在△ABC和△EFD 中,
AB=___
∠A=___
______
∴△ABC≌△EFD( )
EF
∠E
AC=DE
SAS
基础练习(填空题)
A
B
C
D
O
2.如图AC与BD相交于点O,
已知OA=OC,OB=OD,
求证:△AOB≌△COD
证明:
在△AOB和△COD中
OA=OC
______________
OB=OD
∠AOB=∠COD
∴△AOB≌△COD( )
SAS
已知:如图,AB=CB,∠1=∠2
求证:∠A=∠C
例1
A
B
C
D
1
2
证明:
在△ABD 和△CBD中
AB=BC
∠1=∠2
BD=BD
∴△ABD≌△CBD(SAS)
∴ ∠A=∠C (全等三角形的对应角相等)
例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?
A
B
C
E
D
证明:在△ABC 和△DEC中
∴△ABC ≌△DEC(SAS)
∴ AB=DE(全等三角形的对应边相等)
CA=CD
∠ACB=∠DCE
CB=CE
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。
由前边两个题目可以看出:
归纳
1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?
B
D
A
C
证明:∵在△BAD和△BAC中,
BA=BA
∠BAD=∠BAC
AD=AC
∴ △BAD≌△BAC (SAS).
即BD=BC
2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠D
A
D
B
E
F
C
【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE
在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC
∴ △BAD≌△BAC (SAS).
即∠A=∠D
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
探究4
画出一个△ABC,使得AB=5cm, ∠B=30°,
AC=3cm,把你画的三角形与其他同学画的进行比较,它们会全等吗?
A
B
C
D
如图△ABC与△ABD中,AB=AB,AC=BD, ∠B=∠B
他们全等吗?
强调:这个角一定要是这两边所夹的角
到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是:
1、边边边(SSS)
2、边角边(SAS)
小结:
作业
P15 第3题
P16 第10题
