4.2线段、射线、直线(2) 湘教版数学七年级上册 课件(共23张PPT)
文档属性
| 名称 | 4.2线段、射线、直线(2) 湘教版数学七年级上册 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
课前复习
线段
有两个端点,连接两个端点得到的图形就是线段。线段有两个端点且线段是有长度的
射线
将线段向一个方向无限延长就形成了射线。射线有一个端点,只能向一个方向无限延伸。端点字母表示在前,顺序不能颠倒
直线
将一条线段向两个方向无限延伸就形成了直线。直线没有端点,向两个方向无限延伸。
公安部门准备抓捕一名犯罪嫌疑人.如图,犯罪嫌疑人在B 处活动,你作为一名公安干警在A处.听到抓捕指令后,你会选择哪条路进行抓捕?为什么?
【帮一帮】我来当警察
一:情境导入
埃及的塞得港和苏伊士城的直线距离只有一百多千米,但是一片陆地不能行船,轮船必须绕道好望角到苏伊士城,后来人们开挖了苏伊士运河,使轮船航行路程缩短了几千千米,这是根据什么原理?
在广阔的原野上,旅行者要从A点走到B点,
常常会走什么路线?
走直线
动脑筋
线段的基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间,线段最短。
连结两点的线段的长度,叫做这两点之间的距离。
A
B
1.在修路时,通常会将一条弯曲的公路改成直道以缩短路程,其这样做的依据是 。
2、下列说法正确的是( )
A、线段AB叫做点A与点B两点间的距离。
B、线段AB的长度叫做点A与点B两点间的距离。
做一做
小组一起探究比较两根木棒的长短,你有几种方法 每种方法是如何操作的?
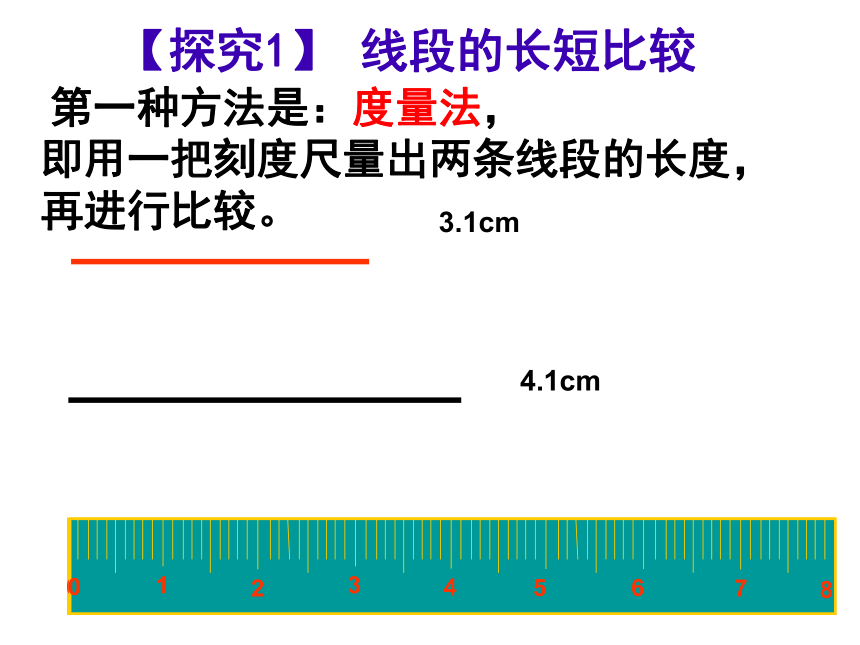
【探究1】 线段的长短比较
二:新知导学,合作探究
第一种方法是:度量法,
即用一把刻度尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
1
2
3
5
4
6
7
8
0
【探究1】 线段的长短比较
第二种方法:叠合法
强调:对齐起点,看终点。
【探究1】 线段的长短比较
像图中这样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
AB小于CD AB < CD
AB 等于CD AB = CD
AB 大于CD AB > CD
C
A
D
B
C
A
D
B
C
A
D
B
总结:比较线段长短的两种方法:
1、度量法——从“数”的角度比较
2、叠合法——从“形”的角度比较
起点对齐,看终点
【探究1】 线段的长短比较
A(C)
B
D
图1
A(C)
B
D
图2
A(C)
B(D)
图3
判断线段AB和CD的大小.
1:如图1,线段AB和CD的大小关系是AB CD;
2:如图2,线段AB和CD的大小关系是AB CD;
3:如图3,线段AB和CD的大小关系是AB CD.
填一填
练一练:如图,点B、C、D依次在线段AE上.
A
B
C
D
E
a
a
b
c
1、AC= ___ + ___
2、CD= ___ - ___
3、AE= ___ + ___
【探究2】 线段的和与差
自主学习:认真阅读课本P120第二段的内容,并完成下面几个小问题:
CE
AC
其中AB=BC=a,CE=b,DE=c.
= ___ + ___
= ___ - ___
= ___ + ___
= ___
4:直线l上有A、B、C三点,线段AB=7cm,线段BC=4cm,线段AC的长度是( B )。
A:3cm
B:11cm
C:3cm或11cm
D:以上都不对
练一练
公元前五世纪的希腊数学家,已经习惯于仅用圆规和没有刻度的直尺来作图了。这种作图我们简称尺规作图。数学家们总是对用简单的工具解决困难的问题备加赞赏。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
例1 如图,已知线段a,借助圆规和直尺作一条线段使它等于2a.
【探究3】 尺规作图
a
作法:
1:作射线AD;
2:在AD上顺次截取AB=BC=a.
则AC就是所要求作的线段
A
D
C
B
1:直尺只用来画线,不能用来度量长度。
3:结论不能少。
2:作法可以不写,但作图痕迹要保留。
已知线段a,b(a>b)(如图)用尺和圆规作一条线段使它等于a-b。
【探究3】尺规作图
b
a
画一画
A
C
B
【探究3】 尺规作图
把一条线段分成两条相等线段的点, 叫做这条线段的中点.(如图点B是线段AC的中点)
等分点的概念
因为 点B是线段AC的中点
所以
AB = BC = AC
AC=2AB=2BC
几何语言:
或
如果把一条线段分成 三 条相等线段的点, 叫做这条线段的___________。
2
四
四等分点
一条线段的 三 等分点有_______个。
三等分点
四
3
n
n
n
(n-1)
A
D
B
C
1.如图,从A地到B地共有三条
路线①②③,其中 最短,
理由是 .
③
①
②
2.比较右图所示的线段的长度:
(1) DC AC;
(2) AD + DC AC;
(3) AD + BD AB;
B
A
C
D
三:巩固练习
A地
B地
3:如图,已知点C为线段AB的中点,则下列式子错误的是( )
A
B
C
B:AB=2AC
A:BC= AB
C:AB=BC
D:AB=2BC
4:线段AB=12cm,点C是线段AB的三等分点,则AC的长度是( )。
C:4cm或8cm
A:4cm
B:8cm
D:以上都不对
三:巩固练习
5:如图,已知点B是线段AC上的一点,点M、N分别为线段AB与BC的中点,若AB=8cm,BC=4cm,则MN=( )cm。
A
M
N
B
C
AC=12cm
AC=a
MN=
MB
+
BN
=
+
=
=
三:巩固练习
6.举出两个例子说明“连结两点的所有连线中,线段最短”这一性质在实际生活中的应用.
AB_____CD; OA_____BC; OA_____OC;
AB_____AD; AD_____BC;
O是线段_____和______的中点.
B
C
A
D
7.量出图中线段AB,BC,CD,AD,OA, OC的长度,然后用“=、>、<”填空:
修公路取直凿隧道等
=
=
=
<
<
AC
BD
O
学完本节课,你有什么收获?
四:课堂小结
如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?依据是什么。
C
●
●
●
●
B
D
A
五:能力提升
课前复习
线段
有两个端点,连接两个端点得到的图形就是线段。线段有两个端点且线段是有长度的
射线
将线段向一个方向无限延长就形成了射线。射线有一个端点,只能向一个方向无限延伸。端点字母表示在前,顺序不能颠倒
直线
将一条线段向两个方向无限延伸就形成了直线。直线没有端点,向两个方向无限延伸。
公安部门准备抓捕一名犯罪嫌疑人.如图,犯罪嫌疑人在B 处活动,你作为一名公安干警在A处.听到抓捕指令后,你会选择哪条路进行抓捕?为什么?
【帮一帮】我来当警察
一:情境导入
埃及的塞得港和苏伊士城的直线距离只有一百多千米,但是一片陆地不能行船,轮船必须绕道好望角到苏伊士城,后来人们开挖了苏伊士运河,使轮船航行路程缩短了几千千米,这是根据什么原理?
在广阔的原野上,旅行者要从A点走到B点,
常常会走什么路线?
走直线
动脑筋
线段的基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间,线段最短。
连结两点的线段的长度,叫做这两点之间的距离。
A
B
1.在修路时,通常会将一条弯曲的公路改成直道以缩短路程,其这样做的依据是 。
2、下列说法正确的是( )
A、线段AB叫做点A与点B两点间的距离。
B、线段AB的长度叫做点A与点B两点间的距离。
做一做
小组一起探究比较两根木棒的长短,你有几种方法 每种方法是如何操作的?
【探究1】 线段的长短比较
二:新知导学,合作探究
第一种方法是:度量法,
即用一把刻度尺量出两条线段的长度,
再进行比较。
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
1
2
3
5
4
6
7
8
0
【探究1】 线段的长短比较
第二种方法:叠合法
强调:对齐起点,看终点。
【探究1】 线段的长短比较
像图中这样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
AB小于CD AB < CD
AB 等于CD AB = CD
AB 大于CD AB > CD
C
A
D
B
C
A
D
B
C
A
D
B
总结:比较线段长短的两种方法:
1、度量法——从“数”的角度比较
2、叠合法——从“形”的角度比较
起点对齐,看终点
【探究1】 线段的长短比较
A(C)
B
D
图1
A(C)
B
D
图2
A(C)
B(D)
图3
判断线段AB和CD的大小.
1:如图1,线段AB和CD的大小关系是AB CD;
2:如图2,线段AB和CD的大小关系是AB CD;
3:如图3,线段AB和CD的大小关系是AB CD.
填一填
练一练:如图,点B、C、D依次在线段AE上.
A
B
C
D
E
a
a
b
c
1、AC= ___ + ___
2、CD= ___ - ___
3、AE= ___ + ___
【探究2】 线段的和与差
自主学习:认真阅读课本P120第二段的内容,并完成下面几个小问题:
CE
AC
其中AB=BC=a,CE=b,DE=c.
= ___ + ___
= ___ - ___
= ___ + ___
= ___
4:直线l上有A、B、C三点,线段AB=7cm,线段BC=4cm,线段AC的长度是( B )。
A:3cm
B:11cm
C:3cm或11cm
D:以上都不对
练一练
公元前五世纪的希腊数学家,已经习惯于仅用圆规和没有刻度的直尺来作图了。这种作图我们简称尺规作图。数学家们总是对用简单的工具解决困难的问题备加赞赏。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
例1 如图,已知线段a,借助圆规和直尺作一条线段使它等于2a.
【探究3】 尺规作图
a
作法:
1:作射线AD;
2:在AD上顺次截取AB=BC=a.
则AC就是所要求作的线段
A
D
C
B
1:直尺只用来画线,不能用来度量长度。
3:结论不能少。
2:作法可以不写,但作图痕迹要保留。
已知线段a,b(a>b)(如图)用尺和圆规作一条线段使它等于a-b。
【探究3】尺规作图
b
a
画一画
A
C
B
【探究3】 尺规作图
把一条线段分成两条相等线段的点, 叫做这条线段的中点.(如图点B是线段AC的中点)
等分点的概念
因为 点B是线段AC的中点
所以
AB = BC = AC
AC=2AB=2BC
几何语言:
或
如果把一条线段分成 三 条相等线段的点, 叫做这条线段的___________。
2
四
四等分点
一条线段的 三 等分点有_______个。
三等分点
四
3
n
n
n
(n-1)
A
D
B
C
1.如图,从A地到B地共有三条
路线①②③,其中 最短,
理由是 .
③
①
②
2.比较右图所示的线段的长度:
(1) DC AC;
(2) AD + DC AC;
(3) AD + BD AB;
B
A
C
D
三:巩固练习
A地
B地
3:如图,已知点C为线段AB的中点,则下列式子错误的是( )
A
B
C
B:AB=2AC
A:BC= AB
C:AB=BC
D:AB=2BC
4:线段AB=12cm,点C是线段AB的三等分点,则AC的长度是( )。
C:4cm或8cm
A:4cm
B:8cm
D:以上都不对
三:巩固练习
5:如图,已知点B是线段AC上的一点,点M、N分别为线段AB与BC的中点,若AB=8cm,BC=4cm,则MN=( )cm。
A
M
N
B
C
AC=12cm
AC=a
MN=
MB
+
BN
=
+
=
=
三:巩固练习
6.举出两个例子说明“连结两点的所有连线中,线段最短”这一性质在实际生活中的应用.
AB_____CD; OA_____BC; OA_____OC;
AB_____AD; AD_____BC;
O是线段_____和______的中点.
B
C
A
D
7.量出图中线段AB,BC,CD,AD,OA, OC的长度,然后用“=、>、<”填空:
修公路取直凿隧道等
=
=
=
<
<
AC
BD
O
学完本节课,你有什么收获?
四:课堂小结
如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?依据是什么。
C
●
●
●
●
B
D
A
五:能力提升
同课章节目录
