江西省九江市柴桑一高2022届高三上学期第二次月考数学(文)试题(Word版含答案)
文档属性
| 名称 | 江西省九江市柴桑一高2022届高三上学期第二次月考数学(文)试题(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 733.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-08 00:00:00 | ||
图片预览



文档简介
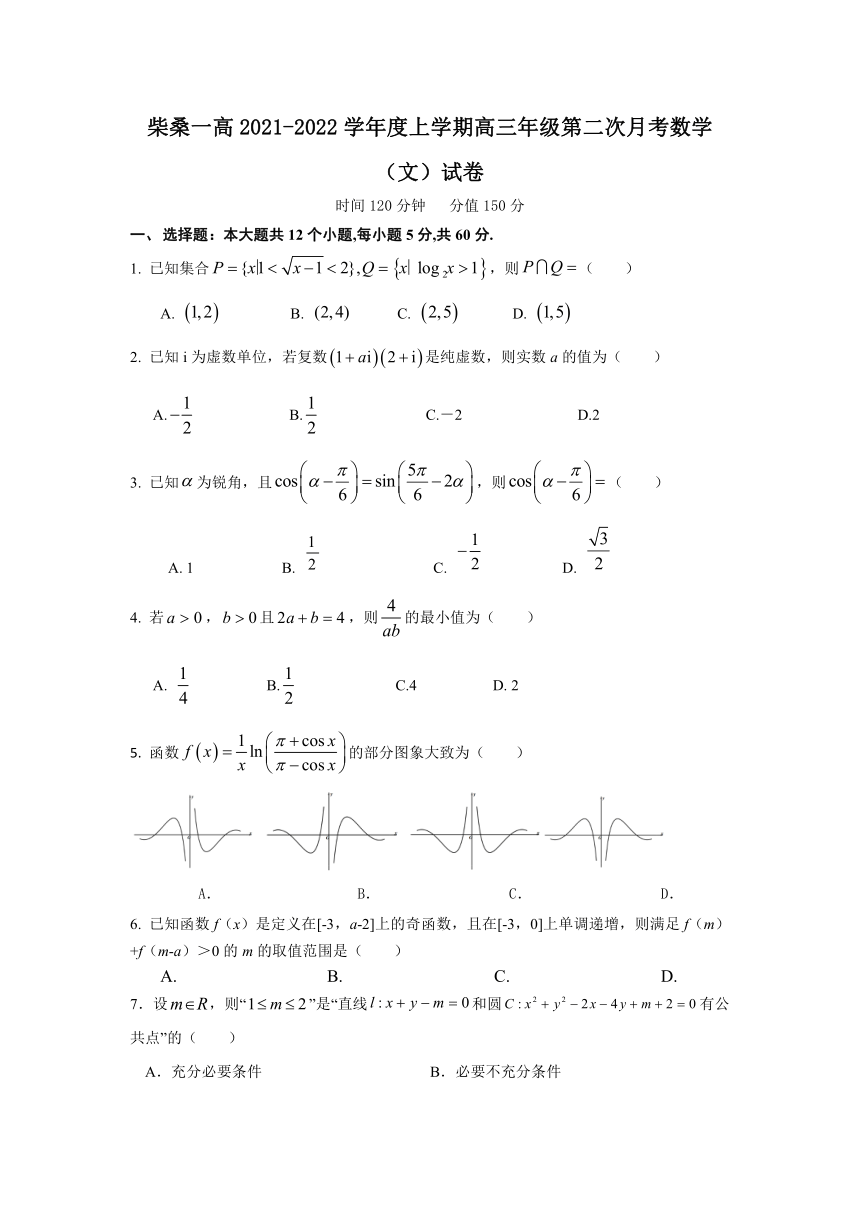
柴桑一高2021-2022学年度上学期高三年级第二次月考数学(文)试卷
时间120分钟 分值150分
1、 选择题:本大题共12个小题,每小题5分,共60分.
1. 已知集合,则( )
A. B. C. D.
2. 已知i为虚数单位,若复数是纯虚数,则实数a的值为( )
A. B. C.-2 D.2
3. 已知为锐角,且,则( )
A. 1 B. C. D.
4. 若,且,则的最小值为( )
A. B. C.4 D. 2
5. 函数的部分图象大致为( )
A. B. C. D.
6. 已知函数f(x)是定义在[-3,a-2]上的奇函数,且在[-3,0]上单调递增,则满足f(m)+f(m-a)>0的m的取值范围是( )
A. B. C. D.
7.设,则“”是“直线和圆有公共点”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
8.已知函数,则( )
A.函数的图像关于直线对称 B.函数的图像关于点对称
C.在上单调递减 D.在上单调递减,在上单调递增
9. 已知函数图象相邻两个对称中心之间的距离为,将函数的图象所左平移个单位后,得到的图象关于轴对称,那么函数的图象( )
A. 关于点对称 B. 关于点对称
C. 关于直线对称 D. 关于直线对称
10.已知是上的奇函数,,则数列的通项公式为( )
A. B. C. D.
11. 已知函数f(x)=,若0<a<b且满足f(a)=f(b),则af(b)+bf(a)的取值范围是( )
A. B. C. D.
12.已知函数的导函数是偶函数,若方程在区间(其中为自然对数的底)上有两个不相等的实数根,则实数的取值范围是
A. B. C. D.
二、填空题(本大题共4个小题,每小题5分,共20分.)
13.设曲线在点(3,3)处的切线与直线ax-y-1=0平行,则a等于__________.
14.命题p:若x>0,则x>a;命题q:若m≤a-2,则m15. 在△ABC中,角A、B、C的对边a、b、c为三个连续偶数且C=2A,则b= .
16.已知是边长为2的等边三角形,D为的中点,点P在线段(包括端点)上运动,则的取值范围是______.
三、解答题(共70分. 第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.)
17.(12分)在中,,,,求:
(1)a的值;(2)和的面积.
18.(12分)已知在数列{an}中,a1=1,a2=3,且当n≥2时,an+1=4(an-an-1)。
(1)证明:{an+1-2an}是等比数列; (2)求数列{an}的通项公式。
19.(12分)已知锐角三角形ABC内角的对边分别为且;
(1)求角;
(2)如图,边的垂直平分线交于,交边于,求长
20.(12分)已知数列为等差数列,是数列的前项和,且,,数列 满足:,当时,.
(1)求数列,的通项公式;(2)令,证明:.
21.(12分)已知函数(其中,是自然对数的底数).
(1)若在点处的切线方程为,求;
(2)若,函数恰好有两个零点,求实数的取值范围.
22.(10分)在平面直角坐标系xOy中,曲线C1的参数方程为(α为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ,曲线C1、C2的公共点为A、B.
(1)求直线AB的斜率;
(2)若点C、D分别为曲线C1、C2上的动点,当|CD|取最大值时,求四边形ACBD的面积.
23.设f(x)=|x-1|+2|x+1|的最小值为m.
(1)求m的值; (2)设a,b∈R,a2+b2=m,求的最小值.
高三年级第二次月考数学(文)答案
1、 选择题:本大题共12个小题,每小题5分,共60分.
1.C 2.D 3.A 4.D 5.A 6.B 7.C 8.B 9.C 10.D 11.C 12.A
二、填空题:本大题共4小题,每小题5分,共20分
13. -2 14. [0,1) 15. 10 16.
三、解答题共6个小题,共70分.
17. 解:(Ⅰ)在中,由余弦定理,得,
解得.
(Ⅱ)∵,,∴.
在中,由正弦定理,得.
∵,,∴,∴.
18
19. 【答案】(1);(2).
20.【解析】:(1)数列为等差数列,是数列的前项和,且,
设数列的首项为,公差为,则:解得:,
所以…2分
因为①
所以当 时,.②
①﹣②得:,由于,整理得(常数).
所以数列是以2为首项,2为公比的等比数列.所以.………6分
证明:(2)由(1)得.……7分
所以①,故②,
①﹣②得:…10分
所以.即……12分
21. 【解析】(1),………………2分
由题意可知,解得………4分
(2),…………5分
问题等价于的图象和直线恰好有2个交点,求的取值范围.
令,则.…………7分
令,则,所以在上单调递减.又,
当时,,,所以在上单调递增.
当时,,,所以在上单调递减,……10分
所以的极大值即最大值为
当时,;当时,
当时,的图象和直线恰好有2个交点,
所以当时,函数恰好有两个零点………………………12分
22.【答案】解:(I)曲线C1的参数方程为(α为参数),消去参数化为:x2+(y-1)2=1.
曲线C2的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,化为普通方程:x2+y2=4x.
上述两个方程相减可得:2x-y=0.
则直线AB的斜率为2.
(Ⅱ)当且仅当直线CD经过两个圆的圆心时,线段CD取得最大值,此时|CD|=3+=+3.
|AB|=2=.
直线C1 C2的方程为:y=-x+1,可得C1 C2⊥AB.
∴当|CD|取最大值时,四边形ACBD的面积S=|AB| |CD|=××(3+)=2+.
23.【答案】解:(Ⅰ)当x≤-1时,f(x)=-3x-1≥2,
当-1<x<1时,f(x)=x+3>2,
当x≥1时,f(x)=3x+1≥4,
∴当x=-1时,f(x)取得最小值m=2;
(Ⅱ)由题意知a2+b2=2,a2+1+b2+1=4,
∴+=(a2+1+b2+1)(+)=[5++]≥,
当且仅当=]时,即a2=,b2=等号成立,
∴的最小值为.
时间120分钟 分值150分
1、 选择题:本大题共12个小题,每小题5分,共60分.
1. 已知集合,则( )
A. B. C. D.
2. 已知i为虚数单位,若复数是纯虚数,则实数a的值为( )
A. B. C.-2 D.2
3. 已知为锐角,且,则( )
A. 1 B. C. D.
4. 若,且,则的最小值为( )
A. B. C.4 D. 2
5. 函数的部分图象大致为( )
A. B. C. D.
6. 已知函数f(x)是定义在[-3,a-2]上的奇函数,且在[-3,0]上单调递增,则满足f(m)+f(m-a)>0的m的取值范围是( )
A. B. C. D.
7.设,则“”是“直线和圆有公共点”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
8.已知函数,则( )
A.函数的图像关于直线对称 B.函数的图像关于点对称
C.在上单调递减 D.在上单调递减,在上单调递增
9. 已知函数图象相邻两个对称中心之间的距离为,将函数的图象所左平移个单位后,得到的图象关于轴对称,那么函数的图象( )
A. 关于点对称 B. 关于点对称
C. 关于直线对称 D. 关于直线对称
10.已知是上的奇函数,,则数列的通项公式为( )
A. B. C. D.
11. 已知函数f(x)=,若0<a<b且满足f(a)=f(b),则af(b)+bf(a)的取值范围是( )
A. B. C. D.
12.已知函数的导函数是偶函数,若方程在区间(其中为自然对数的底)上有两个不相等的实数根,则实数的取值范围是
A. B. C. D.
二、填空题(本大题共4个小题,每小题5分,共20分.)
13.设曲线在点(3,3)处的切线与直线ax-y-1=0平行,则a等于__________.
14.命题p:若x>0,则x>a;命题q:若m≤a-2,则m
16.已知是边长为2的等边三角形,D为的中点,点P在线段(包括端点)上运动,则的取值范围是______.
三、解答题(共70分. 第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.)
17.(12分)在中,,,,求:
(1)a的值;(2)和的面积.
18.(12分)已知在数列{an}中,a1=1,a2=3,且当n≥2时,an+1=4(an-an-1)。
(1)证明:{an+1-2an}是等比数列; (2)求数列{an}的通项公式。
19.(12分)已知锐角三角形ABC内角的对边分别为且;
(1)求角;
(2)如图,边的垂直平分线交于,交边于,求长
20.(12分)已知数列为等差数列,是数列的前项和,且,,数列 满足:,当时,.
(1)求数列,的通项公式;(2)令,证明:.
21.(12分)已知函数(其中,是自然对数的底数).
(1)若在点处的切线方程为,求;
(2)若,函数恰好有两个零点,求实数的取值范围.
22.(10分)在平面直角坐标系xOy中,曲线C1的参数方程为(α为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4cosθ,曲线C1、C2的公共点为A、B.
(1)求直线AB的斜率;
(2)若点C、D分别为曲线C1、C2上的动点,当|CD|取最大值时,求四边形ACBD的面积.
23.设f(x)=|x-1|+2|x+1|的最小值为m.
(1)求m的值; (2)设a,b∈R,a2+b2=m,求的最小值.
高三年级第二次月考数学(文)答案
1、 选择题:本大题共12个小题,每小题5分,共60分.
1.C 2.D 3.A 4.D 5.A 6.B 7.C 8.B 9.C 10.D 11.C 12.A
二、填空题:本大题共4小题,每小题5分,共20分
13. -2 14. [0,1) 15. 10 16.
三、解答题共6个小题,共70分.
17. 解:(Ⅰ)在中,由余弦定理,得,
解得.
(Ⅱ)∵,,∴.
在中,由正弦定理,得.
∵,,∴,∴.
18
19. 【答案】(1);(2).
20.【解析】:(1)数列为等差数列,是数列的前项和,且,
设数列的首项为,公差为,则:解得:,
所以…2分
因为①
所以当 时,.②
①﹣②得:,由于,整理得(常数).
所以数列是以2为首项,2为公比的等比数列.所以.………6分
证明:(2)由(1)得.……7分
所以①,故②,
①﹣②得:…10分
所以.即……12分
21. 【解析】(1),………………2分
由题意可知,解得………4分
(2),…………5分
问题等价于的图象和直线恰好有2个交点,求的取值范围.
令,则.…………7分
令,则,所以在上单调递减.又,
当时,,,所以在上单调递增.
当时,,,所以在上单调递减,……10分
所以的极大值即最大值为
当时,;当时,
当时,的图象和直线恰好有2个交点,
所以当时,函数恰好有两个零点………………………12分
22.【答案】解:(I)曲线C1的参数方程为(α为参数),消去参数化为:x2+(y-1)2=1.
曲线C2的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,化为普通方程:x2+y2=4x.
上述两个方程相减可得:2x-y=0.
则直线AB的斜率为2.
(Ⅱ)当且仅当直线CD经过两个圆的圆心时,线段CD取得最大值,此时|CD|=3+=+3.
|AB|=2=.
直线C1 C2的方程为:y=-x+1,可得C1 C2⊥AB.
∴当|CD|取最大值时,四边形ACBD的面积S=|AB| |CD|=××(3+)=2+.
23.【答案】解:(Ⅰ)当x≤-1时,f(x)=-3x-1≥2,
当-1<x<1时,f(x)=x+3>2,
当x≥1时,f(x)=3x+1≥4,
∴当x=-1时,f(x)取得最小值m=2;
(Ⅱ)由题意知a2+b2=2,a2+1+b2+1=4,
∴+=(a2+1+b2+1)(+)=[5++]≥,
当且仅当=]时,即a2=,b2=等号成立,
∴的最小值为.
同课章节目录
