2.1.2指数函数及其性质 课件
文档属性
| 名称 | 2.1.2指数函数及其性质 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 760.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-15 19:51:44 | ||
图片预览






文档简介
(共18张PPT)
2.1.2 指数函数及其性质
湖南省耒阳市振兴学校
高中数学老师欧阳文丰
制作于2012年9月13日
材料1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x的函数关系是什么
材料2:当生物死后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢
1.指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数
(exponential function),其中x是自变量,函数的定
义域是R。
练习1:下列函数中,那些是指数函数? .
(1) (5) (6) (8)
(1) y=4x
(2) y=x4
(3) y=-4x
(4) y=(-4)x
(5) y=πx
(6) y=42x
(7) y=xx
(8) y=(2a-1)x
(a>1/2且a≠1)
2.指数函数的图象和性质
用描点法画出指数
函数y=2x和 的图象。
y
x
0
y= 2x
y = x
1 2 3 4 5 6 7 8
8
7
6
5
4
3
2
1
-3 -2 -1
-1
-2
-3
y = 2x
x -1 0 1 2 3
y
8
4
2
1
0.5
8
4
2
1
0.5
x -3 -2 -1 0 1
y
y = x
0
1
2
3
-1
-2
-3
1
2
y=2x
的图象
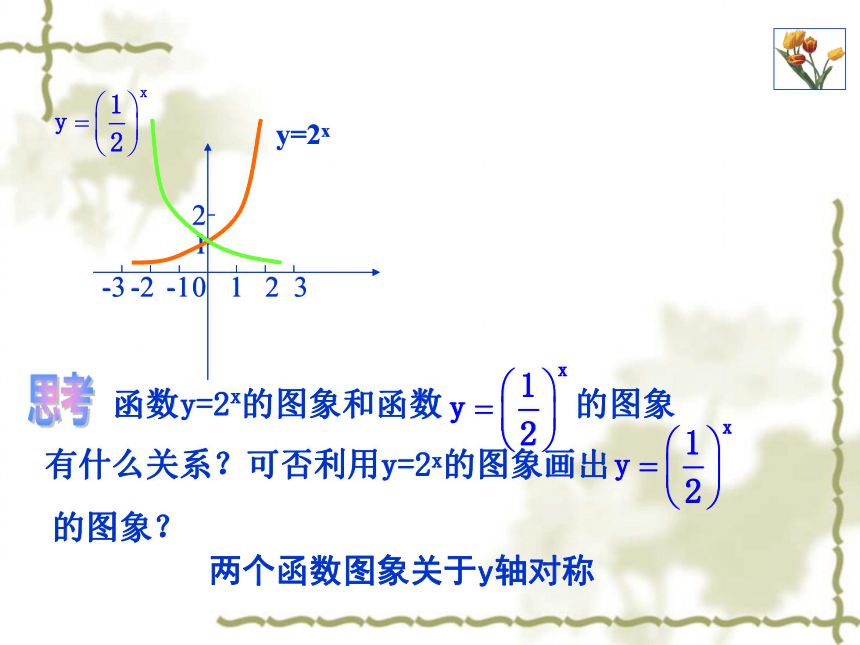
函数y=2x的图象和函数
有什么关系?可否利用y=2x的图象画出
的图象?
两个函数图象关于y轴对称
a>1 0图
象
性
质
R
(0,+∞)
(0,1)
在R上是增函数
在R上是减函数
ax
>1 (x>0)
=1 (x=0)
<1 (x<0)
ax
<1 (x>0)
=1 (x=0)
>1 (x<0)
(1)定义域:
(2)值域:
(3)定点:
(4)单调性:
(5)
函数
值的
分布
情况
指数函数y=ax (a>0,且a≠1)的图象和性质:
y=1
(0,1)
x
O
y
y
y=1
O
x
(0,1)
例6、已知指数函数f(x)=ax (a>0,且a≠1)的图象经过点(3,π),求f(0)、f(1)、f(-3)的值.
例7、比较下列各题中两个值的大小:
(1) 1.72.5,1.73;
(2) 0.8-0.1,0.8-0.2;
(3) 1.70.3,0.93.1.
练习2、求函数y=2x-1的值域
变式:求函数y=2x-1(x>0)的值域
练习3、函数y=ax-3+2(a>0,
且a≠1)必经过哪个定点?
变式:函数y=ax+5-1(a>0,
且a≠1)必经过哪个定点?
例8、截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
年份 经过年数 人口数(亿)
1999 0
2000 1
2001 2
2002 3
… …
1999+x x
y= 13(1+1%)x
练习
1 设y1=a3x+1,y2=a-2x,其中a>0且a 1,确定x为何值时,有
(1)y1=y2 (2)y1>y2
1、指数函数的定义。
2、指数函数简图的作法以及应注意的地方。
3、指数函数的图像和性质。
= = 我!
2.1.2 指数函数及其性质
湖南省耒阳市振兴学校
高中数学老师欧阳文丰
制作于2012年9月13日
材料1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x的函数关系是什么
材料2:当生物死后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系,这个关系式应该怎样表示呢
1.指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数
(exponential function),其中x是自变量,函数的定
义域是R。
练习1:下列函数中,那些是指数函数? .
(1) (5) (6) (8)
(1) y=4x
(2) y=x4
(3) y=-4x
(4) y=(-4)x
(5) y=πx
(6) y=42x
(7) y=xx
(8) y=(2a-1)x
(a>1/2且a≠1)
2.指数函数的图象和性质
用描点法画出指数
函数y=2x和 的图象。
y
x
0
y= 2x
y = x
1 2 3 4 5 6 7 8
8
7
6
5
4
3
2
1
-3 -2 -1
-1
-2
-3
y = 2x
x -1 0 1 2 3
y
8
4
2
1
0.5
8
4
2
1
0.5
x -3 -2 -1 0 1
y
y = x
0
1
2
3
-1
-2
-3
1
2
y=2x
的图象
函数y=2x的图象和函数
有什么关系?可否利用y=2x的图象画出
的图象?
两个函数图象关于y轴对称
a>1 0
象
性
质
R
(0,+∞)
(0,1)
在R上是增函数
在R上是减函数
ax
>1 (x>0)
=1 (x=0)
<1 (x<0)
ax
<1 (x>0)
=1 (x=0)
>1 (x<0)
(1)定义域:
(2)值域:
(3)定点:
(4)单调性:
(5)
函数
值的
分布
情况
指数函数y=ax (a>0,且a≠1)的图象和性质:
y=1
(0,1)
x
O
y
y
y=1
O
x
(0,1)
例6、已知指数函数f(x)=ax (a>0,且a≠1)的图象经过点(3,π),求f(0)、f(1)、f(-3)的值.
例7、比较下列各题中两个值的大小:
(1) 1.72.5,1.73;
(2) 0.8-0.1,0.8-0.2;
(3) 1.70.3,0.93.1.
练习2、求函数y=2x-1的值域
变式:求函数y=2x-1(x>0)的值域
练习3、函数y=ax-3+2(a>0,
且a≠1)必经过哪个定点?
变式:函数y=ax+5-1(a>0,
且a≠1)必经过哪个定点?
例8、截止到1999年底,我国人口约13亿。如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
年份 经过年数 人口数(亿)
1999 0
2000 1
2001 2
2002 3
… …
1999+x x
y= 13(1+1%)x
练习
1 设y1=a3x+1,y2=a-2x,其中a>0且a 1,确定x为何值时,有
(1)y1=y2 (2)y1>y2
1、指数函数的定义。
2、指数函数简图的作法以及应注意的地方。
3、指数函数的图像和性质。
= = 我!
